Abstract
We combine extant theories of evidence accumulation and multi-modal integration to develop an integrated framework for modeling multimodal integration as a process that unfolds in real time. Many studies have formulated sensory processing as a dynamic process where noisy samples of evidence are accumulated until a decision is made. However, these studies are often limited to a single sensory modality. Studies of multimodal stimulus integration have focused on how best to combine different sources of information to elicit a judgment. These studies are often limited to a single time point, typically after the integration process has occurred. We address these limitations by combining the two approaches. Experimentally, we present data that allow us to study the time course of evidence accumulation within each of the visual and auditory domains as well as in a bimodal condition. Theoretically, we develop a new Averaging Diffusion Model in which the decision variable is the mean rather than the sum of evidence samples and use it as a base for comparing three alternative models of multimodal integration, allowing us to assess the optimality of this integration. The outcome reveals rich individual differences in multimodal integration: while some subjects’ data are consistent with adaptive optimal integration, reweighting sources of evidence as their relative reliability changes during evidence integration, others exhibit patterns inconsistent with optimality.
Similar content being viewed by others
Introduction
Humans are constantly confronted with a diverse array of sensory stimuli, each with their own properties known as features. Often, features of a given sensory stimulus vary in the types of perceptual information they convey. Ultimately, we process features with our senses, and depending on the type of feature, we may process the feature in a different part of our brain. For example, visual features are processed through a visual network (i.e., a hierarchy) consisting of several brain regions (e.g., V1, V2), whereas auditory features are processed in an entirely different network (e.g., A1, A2).
Our ability to interact effectively with the world around us depends on how we extract features of stimuli and form a perception of them. This extraction process can be time consuming, so when faced with a life-and-death situation, it’s imperative that we extract the most important features of a stimulus first. The importance of a feature is its diagnosticity, and it will depend on task demands. For example, when looking for a yellow fruit, tactile features like texture of the peel will be less important to the task demands than the visual features like color, and so a good strategy would involve increasing the importance of visual features while decreasing other features. Once we’ve extracted the most important features, we can move on to other features such as gustatory features, which would help use to distinguish between fruits of the same color (e.g. a banana and a lemon).
In addition to the importance of features for given task demands, we must also consider the inconsistency of features as sometimes features can be diagnostic or misleading. For example, when looking for a ripe fruit, a yellow feature is useful for fruits like bananas and lemons, but would lead us astray for fruits like limes. The two aspects of stimulus features, diagnosticity and inconsistency, are often combined combined into the “signal-to-noise ratio”, and more commonly referred to as reliability. To be successful in a given task, an observer must extract the features of the stimulus, weigh them according to their reliability (i.e., their signal-to-noise ratio), and integrate them into a single representation that can be used to facilitate an accurate judgment.
Although little is known about how time interacts with feature integration, a great deal is known about each of their constituent parts. For example, studies of simple perceptual decision making tasks have revealed that the formation of a percept resembles a stochastic accumulation-to-bound process in which the accuracy of the judgment starts at chance and asymptotes within a second or two (Ratcliff 1978; Usher and McClelland 2001; Ratcliff 2006; Kiefer et al. 2009; Gao et al. 2011). The general pattern of results is believed to arise from the gradual summation of noisy evidence for each of the response alternatives, and these conclusions have been drawn from a variety of experimental manipulations targeting the time course of the process (Usher and McClelland 2001; Tsetsos et al. 2012), statistical analyses of empirical choice response time distributions (Van Zandt and Ratcliff 1995; Ratcliff and Smith 2004), and evidence from single-unit neurophysiology (Shadlen and Newsome 2001; Mazurek et al. 2003; Schall 2003).
However, to reduce the complexity of the problem, most studies in perceptual decision making are limited to unimodal – typically visual – stimuli. Other lines of research have examined how information from two or more modalities (i.e., multimodal information) is combined to form a judgment. Such research speaks to the assessment of reliability in the sense that the quality of each modality of information can be experimentally manipulated. To foreshadow, the general conclusion in this literature is that humans and animals are able to integrate multimodal sensory information in an apparently optimal or near-optimal manner (Ernst and Banks 2002; Angelaki et al. 2009a; Witten and Knudsen 2005; Alais and Burr 2004; Ma and Pouget 2008; van Beers et al. 1999; Knill 1998). However, to our knowledge, these multimodal integration studies have allowed a comfortable length of time in which to elicit a judgment. Such a paradigm is limited because the resulting data are manifestations of a representation that has been formed well before a response has been initiated. Hence, these data only inform our understanding of the integration process at its final time point, where presumably, all sources of information have been fully integrated.
The goal of the present article is to examine the time course of multimodal integration from both an experimental and theoretical standpoint. Experimentally, we present the results from a multimodal perceptual decision-making task using the interrogation paradigm, where subjects are required to make a response indicating their judgment at experimentally-controlled points in time. Such a paradigm reveals the time course of the multimodal integration process, which to our knowledge, has not yet been explored. Theoretically, we put forth a new model that describes how multimodal integration might occur over time, and we use it to examine the nature of integration from a mechanistic perspective. We begin by first reviewing the relevant literature from the perceptual decision making and multimodal integration domains.
The time course of evidence accumulation
Although there are many studies investigating multialternative decision making, when studying perceptual decision making, it is often convenient to restrict the stimulus set to two alternatives. Typically, these tasks require subjects to choose an appropriate direction of motion or orientation, such as providing a “left” or “right” response. Currently, the dominant theory of how observers perform these tasks is known as sequential sampling theory (Forstmann et al. 2016). Under this perspective, observers begin with a baseline level of “evidence” for each alternative. Because this baseline level is generally assumed to be independent of the stimuli themselves, the difference in the baselines for each alternative reflects a bias in the decision process, and is subject to experimental manipulations (e.g., Noorbaloochi et al. 2015; Mulder et al. 2012; Van Zandt 2000; Turner et al. 2011). Following the presentation of the stimulus, observers accumulate evidence for each of the (two) alternatives sequentially through time (e.g., Ratcliff 1978; Vickers et al. 1985; Kiani et al. 2008; Laming 1968). Models of perceptual decision making vary widely in the assumptions they make about the precise nature of how evidence accumulates (e.g., Ratcliff 1978; Usher and McClelland 2001; Brown and Heathcote 2005, 2008; Shadlen and Newsome 2001; Merkle and Van Zandt 2006), but they usually assume that the noise present in the integration process follows a Gaussian distribution. Furthermore, at each time point, these models assume that the state of evidence at time t is a noisy summation of all the evidence preceding t (i.e, the sum of the baseline evidence at time 0 up to t; Ditterich 2010; Purcell et al. 2010). Due to the assumptions about the noise in the process and the linear summation, the distribution of the sensory evidence variable at any time t also follows a Gaussian distribution, whose mean and standard deviation increase with t together in a linear fashion (Wagenmakers and Brown 2007).
Experimentally, a common approach to studying perceptual decision making behavior is the so-called free response paradigm. In this paradigm, subjects are given free reign in determining the appropriate time to elicit a judgment. Often, subjects are provided with instructions emphasizing which factor in the task is most important, such as the speed or accuracy of the response, but ultimately, the interpretation of these instructions is subject to a great deal of variability across subjects (e.g., Ratcliff and Rouder 1998). The self-terminating nature of the free response paradigm requires additional elicitation mechanisms from models that embody the core principles of sequential sampling theory. By far the most common assumption is a decision “threshold” that terminates the evidence accumulation process once one of the accumulators reaches its value. At this point in time, a decision is made that corresponds to the accumulator that first reached the threshold.
Despite its productivity, the free response paradigm makes it difficult to appreciate how the evidence accumulation process unfolds over time. One way to obtain a more detailed timeline of the evidence accumulation process is through the interrogation paradigm where subjects are explicitly asked to make a decision at a prescribed set of time points (Gao et al. 2011; Kiani et al. 2008; Ratcliff 2006; Wickelgren 1977). For reasons that we will discuss in the next section, this paradigm is particularly well suited for studying perceptual decision making in the context of multimodal integration.
Multimodal integration
The interrogation procedure will continue to be a relevant tool, given recent proposals about the time course of multimodal integration. For example, many have proposed a temporal window of integration that helps decide whether two or more stimuli will be integrated as one. This window may act as a filtering mechanism: if two or more stimuli are received within a certain amount of time, they will be unified into a single percept. However, if the temporal distance between stimuli is too long, each stimulus will correspond to a distinct percept (Colonius and Diederich 2010; McDonald et al. 2000; Rowland et al. 2007; Ohshiro et al. 2011; Burr et al. 2009). To explain this integration dynamic, Colonius and Diederich (2010) proposed the time-window of integration model, that assumes multimodal perception starts with a race between peripheral sensory processes. If these sensory processes finish together within a certain time window, the stimuli will be integrated (Colonius and Diederich 2010). Although the time-window of integration model is useful for identifying the boundary conditions of integration, the uncertainty surrounding the bounds of this window leave much to be desired. For example, some estimates of the window width range from 40 to 1500 ms (Colonius and Diederich 2010), which span the effective time period for decision making in many perceptual decision making tasks.
There also exists an important terminological distinction in multimodal integration involving the terms integration and interplay. Integration refers to cases in which features converge together to form a single percept, whereas interplay refers to cases where one stimulus affects the perception of another, but is not combined with it. For example, experiments have shown that touch at a given location can improve judgments about color, even though touch cannot carry color information and would not be integrated into a touch-color percept (Driver and Noesselt 2008; Spence et al. 2004). These experiments rely on multimodal interplay and not multimodal integration.
Perhaps the most inconsistent aspect of the literature surrounding multimodal integration is the issue of optimality. Many experiments on multimodal integration are constructed around the issue of stimulus reliability, which is commonly defined as the inverse of the stimulus variance (Fetsch et al. 2011; Driver and Noesselt 2008; Ernst and Banks 2002; Drugowitsch et al. 2015). When combining information from one or more sources, the brain must acknowledge that inputs may vary not only in their modality, but also in their reliability. Testing performance then entails examining whether or not subjects can appropriately assign importance or “weight” in proportion to the reliability of stimulus features (Ma and Pouget 2008). Apparently, the optimal method of assigning weights is to inversely relate them to the reliability of the features, and then combine the weighted representations according to Bayes rule (Fetsch et al. 2011; Pouget et al. 2002; Angelaki et al. 2009b; Battaglia et al. 2003; Angelaki et al. 2009a). However, the process of assigning weights is difficult to study experimentally, especially in cases where cue reliability is being actively manipulated. In such cases, the assignment of weights is likely to be a dynamic process, where weight values vary throughout the experiment. Experimenters have tested multimodal integration in a variety of settings, where visual, auditory, haptic, vestibular, proprioceptive, gustatory, or olfactory features serve as the stimuli. Despite the wealth of literature on the topic, however, the breadth of experimental manipulations make it difficult to conclude the robustness of the optimality of integration. Furthermore, there are several inconsistencies in the evaluation of how closely predictions from a model using an optimal integration algorithm must match the empirical data to still be considered optimal.
Both optimal and sub-optimal integration have been observed in many different paradigms, underscoring the demand for further investigation. One specific example that is closely related to our experiment is an audio-visual localization task in which subjects are instructed to make a choice between left and right. Studies on multimodal integration argue that subjects keep track of the “estimation” of a stimulus; for example, the estimation of a car’s position as it is driven somewhere either to the left or right of the perceiver. Suppose the estimation given visual information is given by p(x|v), and the estimation given independent auditory information is given by p(x|a). In this case, the optimal estimation based on both visual and auditory information p(x|v,a) should follow Bayes’ rule. If both estimations are Gaussian with means μ v and μ a and standard deviations σ v and σ a , then the resulting optimal estimation should also be Gaussian with mean
Many authors, including Ernst and Banks (2002), Angelaki et al. (2009b), Witten and Knudsen (2005), Alais and Burr (2004), and Ma and Pouget (2008) have explored this formulation. As discussed more fully under hypothesis 1 below, the weight on one modality (e.g., the visual modality) is proportional to the relative size of the variance in the other modality (in this case, visual), so that the more reliable modality – the one with the smaller variance – receives the greater weight. To see how bimodal information can help, we can imagine the case of congruency, where the visual and auditory estimations are both centered at the actual location μ of the stimulus and are equally reliable with standard deviation σ. The estimation based on bimodal information will then be centered at the same place μ with a sharper standard deviation \(\sigma /\sqrt {2}\). Therefore, the probability of making the correct choice is higher with bimodal information.
Audio-visual localization tasks sometimes produce patterns of data that are considered optimal (Bresciani et al. 2008; Alais and Burr 2004), and sometimes produce sub-optimal patterns (Bejjanki et al. 2011; Battaglia et al. 2003). To make things more confusing, a weighting strategy that may be optimal for some situations may not be optimal for others. For example, Witten and Knudsen (2005) suggested that a particular sub-optimal pattern they observed was evolutionarily appropriate, arguing that visual information, being inherently more reliable than other modalities in spatial tasks, should have relatively larger weights. They reasoned that while this weighting strategy may result in sub-optimal performance in a particular setting, it could still be considered optimal from an integration stand point. Only when the visual cue becomes significantly less reliable than its auditory counterpart does this particular weighting strategy become sub-optimal (Battaglia et al. 2003).
Another example is the heading discrimination paradigm where subjects had to determine the direction they faced using a combination of visual and vestibular information. In some cases, subjects optimally adjusted their weights according to the changing reliability of the visual cue (Angelaki et al. 2009b) while some subjects integrated sub-optimally, assigning too much weight to either the visual or vestibular cue (Drugowitsch et al. 2015; Fetsch et al. 2011; Fetsch et al. 2009). As for other modalities, experiments have shown that primates may integrate visual and haptic information optimally. For example, one such study examined visual, auditory, and haptic integration in the rhesus monkey. This study selected the superior colliculus as a target for single-neuron recordings because previous work involving sensory convergence in primates and cats identified the superior colliculus as an important hub for integration, likely due to its connections to various sensory processes (Meredith and Stein 1983; Jay and Sparks 1984). In a bimodal condition involving visual and somatosensory cues, neurons in the superior colliculus optimally adjusted their sensitivity and firing patterns according to the reliability of each stimulus (Wallace et al. 1996). Another study showed a similar result in humans, demonstrating optimal visual-haptic integration (Ernst and Banks 2002). An additional structure proposed to be a hub for integration is the dorsal medial superior temporal area, or the MSTd. The MSTd is thought to receive vestibular and visual information related to self-motion and also plays a role in heading discrimination tasks (Gu et al. 2008). Single neuron recordings during visual-vestibular integration tasks revealed that these cells may also optimally adjust their firing patterns and sensitivity in response to changes in the cue (Fetsch et al. 2011; Angelaki et al. 2009b).
Filling the gap
From each of the sections above, we have emphasized the need for considering two types of integration. The first type of integration deals with the summation of noisy stimulus information from one time point to the next. This type of integration gives rise to the latent evidence for each response alternative, and ultimately determines the response and response time in classic perceptual decision making tasks. The second type of integration deals with how multiple sources of information from different modalities are combined to form a representation of, say, stimulus location. In this case, “integration” refers to the weighed, normalized sum of the representations corresponding to each modality. In the sections outlined above, we have discussed formal, mathematical models that describe how each of these two types of integration might occur independently, but the question of how best to combine these models remains an open question.
To address this question, and in order for the two lines of research to connect, we propose the Averaging Diffusion Model (ADM) for perceptual decision making. The model is based on the central tenants of the classical diffusion decision model (Ratcliff 1978), as that model was originally applied to the interrogation procedure, but makes a different assumption about how evidence is accumulated (i.e., integrated) over time. Instead of assuming that the evidence is summed over time, the ADM assumes that the evidence is averaged. This seemingly trivial modification has meaningful theoretical implications; specifically, ADM assumes that perceptual decision making is inherently a denoising or filtering process, such that the judgment of a certain feature of the stimulus is based on a representation that gets sharper over time. As will become clear below, this change of perspective allows us to connect directly with models of multimodal integration, allowing for a fully integrated framework.
In addition to developing the ADM, we also present the results of an experiment on multimodal integration with three conditions: a visual only condition, an auditory only condition, and an audiovisual condition, in which congruent auditory and visual information are presented simultaneously. In each condition, stimuli could be presented at four locations, two to the left of a reference point, and two to the right, and in each case the participant’s task was to decide whether the location was left or right of the reference point. Crucially, the task was performed in the interrogation paradigm, where response cues occurred at either 75, 150, 300, 450, 600, 1200, or 2000 milliseconds after stimulus onset. As discussed above, this paradigm provides us with a rich dataset from which we can fully appreciate how multimodal integration unfolds over time. We use the ADM framework to test different assumptions about how the representations formed in each of the two unimodal conditions are combined to form a representation used in the bimodal condition.
The rest of this article is organized in the following way. First, we present the details of the ADM, motivating its use by describing the accumulation process used in the classic DDM. This initial section describes how the ADM accumulates noisy evidence from unimodal stimuli, and how it diverges from the classic DDM. Second, we extend the presentation of the ADM by discussing several ways in which multiple modalities of information can be integrated. Specifically, we propose three ways of performing modality integration, which creates three variants of the ADM. Third, we present the details of our experiment, and discuss the patterns present in the raw data. Finally, we compare the fit of the three variants of ADM via conventional model fit statistics (i.e., the Watanabe-Akaike information criterion), and provide some interpretation for how modality integration is performed across the data in our experiment. We close with a general discussion of the implications and limitations of our results.
Model
The model is conceptually similar to the classic DDM (Ratcliff 1978), but has a slightly different assumption about how the distributions of sensory evidence are mapped onto an overt response. We will now compare and contrast the classic DDM with our averaging model.
The diffusion decision model
As mentioned in the introduction, many studies converge in demonstrating that – within a single modality – information integration across time is imperfect, in one or more different ways. Furthermore, many studies have converged on the idea of sequential sampling theory where observers gradually accumulate information to aid them in choosing among several alternatives. Suppose there are two types of stimuli S R and S L (e.g., a rectangle positioned to the right or left of a central reference point, respectively), and two possibilities of choice responses R R and R L . Many models of decision making assume that, on the presentation of a stimulus S, noisy samples of sensory evidence are accumulated throughout the course of the trial, and these samples are integrated to guide the decision process. Perhaps one of the simplest ways of describing this process of evidence integration is in terms of the differential equation
where a(t) is the value of the integrated evidence variable at time t, μ s represents the mean of the noisy samples, and σ w is the standard deviation of within-trial sample-to-sample variability in the samples of evidence. For the two types of stimuli, we might arbitrarily assume that
Let us assume, following (Ratcliff 1978) that subjects integrate according to this expression from the time the sensory evidence starts to affect the evidence accumulators until the go cue precipitates a decision. This leads to a time-dependent distribution of the sensory evidence variable such that \(a(t)\sim \mathcal {N}(\mu (t), \sigma (t))\), where
When subjects are asked to provide a response, a rightward choice R R is thought to be made when the sensory evidence variable a(t) is greater than some criterion c(t), and a leftward choice R L is made otherwise.
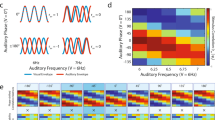
The left panel of Fig. 1 illustrates how the distribution of sensory evidence variable a(t) evolves over time for the DDM. In the beginning, the distribution of evidence has relatively little variance, and the location of potential belief states are concentrated on μ(t). As time increases, the cumulative amount of moment-to-moment noise increases, which directly impacts the dispersion of the sensory evidence variable a(t). Figure 1 also shows how these representations interact with the criterion c(t), which is illustrated by the vertical black line.
A comparison of the DDM and the ADM. The left and right panels show a graphical illustration of the evolution of the sensory evidence state a(t) (x-axis) as a function of time (y-axis) for the DDM (left panel) and the ADM (right panel). For illustrative purposes, we set σ w =0.8, σ b = σ 0=0, and μ s =[−1.5,1.5]
Independent of the value of c(t), the level of discriminability \(d^{\prime }(t)\) evolves according to the following equation:
As time increases, \(d^{\prime }(t)\) increases without bound, thereby predicting infinite discriminability (i.e., error-free performance) at long integration times. While very easy stimuli allow for error-free performance given sufficient processing time, the stimuli used in many psychophysical studies do not. Yet, the model as stated so far predicts that even the most difficult stimuli, if integrated for long enough, should allow error-free performance. There are now three prominent approaches to addressing this deviation from optimality.
First, Ratcliff (1978) proposed that there may be variability from trial to trial in the drift rate parameter. That is, a trial-specific value of μ is taken to be sampled from a Gaussian distribution with mean μ s and standard deviation σ b , where σ b is referred to as the between-trial drift variability parameter. While this between-trial variability can be attributed to the stimulus itself, in many studies the mean stimulus value (e.g., position in screen coordinates) does not vary at all from trial to trial, implying that some factor internal to the observer (e.g., trial-to-trial variability in the representation of the reference position) must be the source of the limitation on performance. Other findings (e.g., Ratcliff and McKoon 2008) suggest that, at the beginning of integration, the decision variable may have some initial variability. Often this is also assumed to be Gaussian, with mean 0 and standard deviation σ 0. Incorporating these additional sources of variability into the DDM, looking across many experimental trials, the distribution of the accumulated evidence variable a(t) still evolves according to a normal distribution with mean μ(t) = μ s t, but its standard deviation is
With these assumptions, it follows that
In other words, as t increases, the effects of both the initial variability and the moment-to-moment or within-trial variability become negligible, and accuracy is ultimately limited by the between-trial variability. Hence, the additional sources of variability allow the model to account for the leveling off of accuracy at long decision times.
The second – not mutually exclusive – possibility is that subjects stop integrating evidence before the end of a trial once the absolute value of the decision variable a(t) exceeds a decision threshold (Mazurek et al. 2003; Ratcliff 2006). All models assume some stopping criterion for free-response paradigms, when the timing of the response is up to the subject. In the interrogation procedure, however, there is no need to stop integrating evidence before the go cue occurs, and stopping integration earlier can only reduce the discriminability \(d^{\prime }\). The use of such a threshold is still possible however, and it offers one way to explain why time-accuracy curves level off. However, we will not investigate models that use the thresholding process in this article.
The third possibility is in the way information is integrated. While the DDM assumes that the evidence for each alternative is accumulated in a perfectly anti-correlated fashion, other models assume a competitive process among accumulators where the evidence for each alternative can arrive at different times (Vickers 1979; Merkle and Van Zandt 2006), inhibit or excite the amount of evidence for an opposing accumulator (Usher and McClelland 2001; Brown and Heathcote 2005; Shadlen and Newsome 2001), or have a completely independent race process (Brown and Heathcote 2008; Reddi and Carpenter 2000). Furthermore, plausible mechanisms such as passive loss of evidence (i.e., “leakage”) have been considered by other models with similar accumulation dynamics (Usher and McClelland 2001; Wong and Wang 2006). Across various architectures, ranges of parameter settings can allow these models to predict a natural leveling off of the time-accuracy curves. Although we feel that the dynamics of these models are very interesting, we will not consider them further in this article. Instead, we will focus on an adaptation of the DDM with starting-point, between-trial, and within-trial variability as reflected in Eq. 1 as it is very widely used and provides good descriptive fits to behavioral data (Ratcliff and McKoon 2008).
The averaging diffusion model
We can now adapt the DDM as described above by transforming the decision variable into the framework often used in multisensory integration studies by dividing the amount of accumulated evidence a(t) by the elapsed time t, measured in seconds. We denote this new variable \(\hat {\mu }(t)\) because it is an estimate of the mean of the stimulus variable μ(t). The expected value of \(\hat {\mu }(t)\) is constant and equal to μ s , while its standard deviation decreases with the square root of time: \(\sigma (t) =\sigma _{w}/\sqrt {t}\). The decrease in the standard deviation of the estimate of the stimulus variable makes it less and less likely that the evidence value will be on the wrong side of the decision criterion at 0, therefore accounting for the increase in \(d^{\prime }\) as time increases. We call this transformed version of the DDM the Averaging Diffusion Model (ADM), to represent the fact that the model assumes participants attempt to estimate the mean of the stimulus input value.
As in the standard DDM model discussed above, a between-trial variability parameter σ b can allow the ADM to account for limitations in performance (i.e., \(d^{\prime }\) reaching a finite asymptotic value) as time increases. Also as in the DDM, the ADM can accommodate initial or starting point variability. For our purposes, we assume this initial variability to be drawn from a Gaussian distribution with mean 0 and standard deviation σ 0. Incorporating these additional sources of variability into the ADM, the expected value of the representation variable a(t) rapidly converges to μ s , while the standard deviation changes as follows:
This equation shows that as t increases, the initial variability σ 0 and the moment-to-moment or within-trial variability σ w become negligible, leading σ(t) to converge to σ b , such that
Hence, as in the DDM, accuracy in the ADM is ultimately limited by the between-trial variability, allowing this model to predict an asymptotic \(d^{\prime }\) for large integration times.
The right panel of Fig. 1 illustrates how the distribution of sensory evidence variable a(t) evolves over time for the ADM. In the beginning, the distribution of evidence is relatively more variable due to the initial starting point noise, making the location of potential beliefs disperse around μ(t) due to having only averaged a few noisy samples. As time increases, the number of noisy samples increases, and the estimate of the mean of the samples becomes more accurate. The model expresses this increased accuracy through the decrease in the variance of the representations. Similar to the DDM discussed above, in modeling responses that occur at particular times in our behavioral experiment, we assume the participant chooses one response alternative if the evidence variable a(t) is greater than a particular criterion at the time the response is triggered, and chooses the other response otherwise. In Fig. 1, the criterion c(t) is set to zero and is illustrated by the vertical line in both panels.
Accounting for bias and temporal delay in evidence integration
Two additional considerations unrelated to the main focus of our investigation need to be taken into account in providing a complete fit to the experimental data (i.e., all response probabilities, not just discriminability data). The first of these is the presence of biases (which vary between participants) that may favor one response over the other. Because we are primarily interested in explaining how stimulus information is integrated over time and across stimulus modalities (i.e., visual or auditory), we will use a simple mechanism for capturing bias, although other more systematic mechanisms are possible in the signal detection theory framework (e.g., Treisman and Williams 1984; Mueller and Weidemann 2008; Benjamin et al. 2009; Turner et al. 2011). Specifically, we will assume that the mean of the sensory evidence variable evolves according to the following equation:
Equation 5 shows that, in addition to the stimulus information S, the model has parameters that allow for a static bias in the mean of the evidence variable (i.e., β 1) as well as a decaying bias parameter which captures an initial bias that becomes negligible as t increases. Although we did investigate other forms of systematic biases over time, the aforementioned mechanism provided a reasonably good account of the data, and as a consequence, we will not discuss these other alternatives.
Finally, care needs to be taken in relating the time t r s at which the response signal is presented to the timing and duration of the evidence accumulation process. For this purpose, we adopt the common assumption that the evidence accumulation process begins after an encoding delay following stimulus onset and ends after a fixed decision delay following the presentation of the go cue, at which time the state of the evidence variable is read out and used to determine the participant’s choice response. The difference between these encoding delay and the decision delay is called τ.Footnote 1 Note that the evidence delay could be longer than the decision delay, in which case the decision could be executed before evidence accumulation begins if the response signal comes very soon after stimulus onset. Because the delay prior to the start of evidence accumulation can vary across participants and across modalities due to differences in modality-specific input pathways, different values of τ are estimated for each modality for each participant. When modeling the state of the decision process at the time of a particular response signal t r s measured from stimulus onset, the time variable t in Eqs. 3 and 5 is adjusted to t r s −τ whenever t r s ≥(τ + 𝜖). When t r s <(τ + 𝜖), this corresponds to the situation were the state of the evidence variable is interrogated before evidence accumulation has had a chance to begin. In this case, t is set to 𝜖, where 𝜖 is small enough that β 0 and σ 0 dominate the initial state of the evidence variable a(t). The (small) constant term 𝜖 is necessary to avoid dividing by zero in Eqs. 3 and 5 above. In all of the model fitting below, we set 𝜖=0.001.
Integrating multiple modalities
With a description of how the ADM accounts for unimodal (i.e., coming from one source) stimuli, we can begin to consider how the model should be extended to account for how observers integrate multimodal (i.e., coming from multiple sources) stimuli. Specifically, we will consider three hypotheses for how observers integrate two sources of information – visual and auditory – in forming their decisions. Furthermore, our hypotheses will consider how observers achieve real-time optimal integration of two different sources of evidence. For example, it is conceivable that observers could employ a dynamic reweighting of the input to a single cross-modal integrator in order to weigh one stimulus input more highly at earlier times and the other stimulus input more highly at later times. However, specific mechanisms for this dynamic reweighing process across time have yet to be proposed. Recently Ohshiro et al. (2011) have proposed how a population of competing multisensory integrators might automatically reweigh evidence according to its reliability, but without considering the time course of processing. As part of our modeling investigation, we consider whether our data is consistent with dynamic reweighting. In the discussion below we consider how such reweighting might be incorporated into the Ohshiro et al. (2011) model.
Because we will be considering both unimodal and bimodal stimuli, a word on notation is in order here. Henceforth, we will subscript the various model quantities with either a “v”, “a”, or “b” to represent the visual, auditory, or bimodal conditions, respectively. For example, the mean of the sensory evidence variable at time t in the auditory condition will be denoted μ a (t). Table 1 provides a complete list of the notation used to represent the variables throughout the article. In the descriptions of the model variants for stimulus integration below, we assume that each unimodal condition has been considered independently, and so μ k (t) and σ k (t) are separately evaluated for each condition (i.e., k={a,v}). In all of the model variants we fit below, separate parameters were used in the auditory and visual modality conditions for β 0, β 1, σ 0, σ b , σ w , and τ. However, these parameters were not free to vary in the bimodal condition. Instead, for the bimodal condition, the relevant variables were calculated as a function of the equations describing the representations used in the two unimodal conditions, in accordance with the three integration hypotheses considered below.
Hypothesis 1: Adaptive optimal weights
The first method of stimulus integration we investigated was the Adaptive Optimal Weights (AOW) model. The AOW model assumes that at each time point the observer combines the evidence from each of the two modalities in a way that reflects the reliability of each modality. To do so, the model relies on a term that expresses the ratio of variability within a specific modality relative to the total amount of variability in the inputs. For example, the variability in the auditory representation is \({\sigma _{a}^{2}}(t)\), whereas the total variability in all the inputs is \({\sigma _{a}^{2}}(t) + {\sigma ^{2}_{v}}(t)\). Hence, the ratio of these variabilities is \({\sigma _{a}^{2}}(t) / \left [ {\sigma _{a}^{2}}(t) + {\sigma ^{2}_{v}}(t) \right ]\). The intuition behind this term is that as the auditory features of the stimulus become more noisy relative to the visual features, this term increases above 0.5, and as the auditory features become less noisy relative to the visual features, this term decreases below 0.5. Using the relation
we can use the ratio of variabilities within each modality to express how cues are combined in an optimal manner (e.g., Ma and Pouget 2008; Landy et al. 2011; Witten and Knudsen 2005). Building on this intuition, in the bimodal condition, the mean μ b (t) and standard deviation σ b (t) of the stimulus representation are
Hence, the evidence variable in the bimodal condition \(a_{b}(t)\sim \mathcal {N}(\mu _{b} (t), \sigma _{b}(t))\) will reflect the optimal weighted combination of the two unimodal evidence variables a a (t) and a v (t). Equations 6 and 7 reflect a cue weighting strategy that is considered “optimal” in the sense that the modality with the least amount of variability is given a greater amount of weight when both modalities appear together, as in the bimodal condition. Equations 6 and 7 are also optimal in the sense that they produce the highest possible discriminability \(d^{\prime }(t)\) curve for each value of t.
The weighting terms applied to the visual and auditory modalities in Eq. 6 may seem counterintuitive given that the variance for the visual stream is used in the numerator of the weighting term applied to the auditory mean (i.e., the rightmost term), whereas the variance for the auditory stream appears in the numerator in the term applied to the visual stream. The reason for this is that the variance in the modality is inversely related to the reliability of the corresponding modality. As an example, suppose the auditory modality is perfectly reliable such that σ a =0, and the visual modality is not perfectly reliable such that σ v = q where q>0. Here, regardless of the value of q, the weighting term applied to the visual modality becomes zero and all attention should go to the auditory modality. This is desirable in the model because as in this example, the auditory modality is weighted more heavily, as it is the more reliable modality.
Hypothesis 2: Static optimal weights
The AOW model above maintains that observers base their integration strategy on the reliability of each unimodal feature at the moment the decision must be made. Another possibility is that subjects adopt a single fixed weighting policy that maximizes overall response accuracy across all possible decision times. While the AOW policy will result in optimal cue weighting at each time point, this alternative policy can be considered optimal subject to the constraint that the weight assigned to each modality is fixed or static regardless of the reliability of the unimodal evidence at any given moment. We refer to this strategy as the Static Optimal Weight (SOW) model.
For this and the subsequent model, a new parameter α is introduced. As in the AOW model above, we parameterize the weights associated with each modality so that they sum to one, or α v + α a =1. Given this constraint, we (arbitrarily) choose α = α v to represent the weight allocated to the visual modality, such that α a =1−α. Since α is assumed fixed for different time points during evidence accumulation, we use it to replace the time-specific terms in Eqs. 6 and 7 to describe the mean and standard deviation of the evidence variable at time t as
respectively.
To determine the value of α that maximizes accuracy, we first define a “response loss function” ξ(t), given by
Equation 10 calculates the probability of making a response for each of the different values of S, which can take any of values {−2,−1,1,2} across trials (S is always the same for both modalities within a trial). Specifically, if the stimulus is to the right (i.e., S is positive as in Fig. 1), ξ(t) is the proportion of the total area of the sensory evidence distribution that is greater than zero, whereas if the stimulus is to the left (i.e., S is negative as in Fig. 1), ξ(t) is the proportion of the area of the sensory evidence distribution that is less that zero. In both cases, ξ(t) represents the probability of making a response that is consistent with the true state of the stimulus. In other words, ξ(t) is the probability of making the correct response. In theory, we could calculate ξ(t) at every possible time point and select the value of α that optimizes ξ(t) for every stimulus value, where
However, this may not lead to the actual optimal policy given the set of specific time points sampled in our experiment. Therefore, we calculate α ∗ by summing up the probabilities at each (discrete) time point used in the experiment:
Once α ∗ has been determined, it is used in Eqs. 8 and 9 to calculate μ b (t) and σ b (t).
Hypothesis 3: Static free weights
The weighting strategies used by the AOW model and the SOW both assume an optimal integration of unimodal cues, and these weighting strategies are both deterministic in the sense that they are completely determined by the parameters from the unimodal conditions, carried over directly into the bimodal condition. However, in the presence of two cues, observers may not necessarily integrate them optimally. In one extreme, they may decide to rely exclusively on one cue over another, since considering both cues simultaneously may impose extra processing demands on participants (cf. Witten and Knudsen 2005). Given these considerations, as well as some of the aforementioned discrepancies in what is considered optimal, our third model explicitly parameterizes the weighting process.
The inclusion of this additional model provides for a stronger test of optimality of integration. The models considered above are limited in the sense that they provide only weak evidence about the extent to which a participant’s strategy is optimal. That is, by assuming a deterministic combination function, we can only evaluate the fidelity of our assumption by comparing the model fit to empirical data, but it does not give us the freedom to explore whether some other cue-combination strategy is more likely to account for the data. Because we have data from this bimodal condition, instead of assuming a direct mapping from unimodal conditions to the bimodal one, we can infer the most-likely weighting policy, conditional on the data. While in principle it is possible that participants choose non-optimal weights for each value of the decision time parameter t, considering this possibility would result in excessive model freedom. Instead we consider the simple possibility that each participant chooses a single value of the fixed weighting parameter α, corresponding to a fixed assignment of weight to signals arising from the auditory and visual modalities. As in the SOW model above, we parameterize the weights associated with each modality so that they sum to one, and choose α to represent the weight allocated to the visual modality such that the weight assigned to the auditory modality is 1−α. As in the SOW model, we describe the mean and standard deviation of the evidence variable at time t as
respectively. We call this model the Static Free Weights (SFW) model, because the weight α is freely estimated on a subject-by-subject basis, but remains static or fixed for all time points within each participants’ data.
The “sum-to-one” constraint on the weights naturally constrains α ∈ [0,1], which allows us to compare α to a reference point of 0.5. Specifically, when α>0.5, the visual modality is given more weight relative to the auditory, and when α<0.5, more weight is given to the auditory modality. In addition, the sum-to-one constraint allows us to directly compare the estimate of the parameter α to the optimal integration strategy assumed by the SOW model and by the AOW as discussed below.
Evaluating the likelihood function
Once μ k (t) and σ k (t) have been evaluated for each stimulus modality condition (i.e., evaluated for all k∈{a,v,b}), we can determine the likelihood of the data given the model parameters. In each of the model fits, the likelihood is expressed as a function of the model parameters, given the full set of response probability data. We denote the number of stimulus presentations in the ith stimulus difficulty condition at the tth integration time in the kth stimulus modality condition as S i,k (t) and the number of “rightward” responses to the S i,k (t) stimuli as R i,k (t). To determine the response probability predicted by the model in the ith stimulus difficulty condition at the tth integration time in the kth stimulus modality condition (denoted R P i,k (t)), we evaluate the following equation:
the set of response probabilities predicted by the model. Although not explicit in the notation, μ k (t) and σ k (t) are evaluated through a set of model parameters 𝜃 and the equations detailed in the above sections. Because the responses are binary, we can evaluate the probability of having observed the data from a given experiment under a particular model with parameters 𝜃 through the binomial distribution. Specifically, we calculate
where Bin (x|n,p) represents the probability of having observed x “successes” in n observations with a single-trial success probability of p, which is given by
This expression is evaluated for all values of i and k as specified above. Finally, we can combine all of the data and model predictions by multiplying the densities together, which forms the likelihood function
where D contains the data from a given experiment (i.e, D={R,S}).
Bayesian prior specification
Because we fit each of the three models to data in the Bayesian paradigm, we were required to specify priors for each of the model parameters. Although one could easily implement a hierarchical version of the model that allows information to be exchanged from one subject to another, we chose not to develop a hierarchical model due to the limited number of subjects in our experiment. To obtain the unimodal parameters needed to fit the three models of bimodal integration listed above, we must specify priors for six parameters (see Table 1). Specifically, we need priors for the between-trial variability parameter σ b , the within-trial variability parameter σ w , the initial starting point variability parameter σ 0, the two bias parameters β 0 and β 1, and the nondecision time parameter τ. Some of the model parameters naturally have restrictions to obey; for example, the standard deviation parameters must be positive. To facilitate estimation of the posterior distribution for such parameters, we applied a logarithmic transformation (cf. Gelman et al. 2004). To avoid the possibility that a poor model fit would arise solely as a result of a poorly chosen prior, we manually adjusted the prior distribution for each parameter so that predicted response curves generated from the model encompassed the range of unimodal data patterns found in the experiment reported here (i.e., see Fig. 2) and in other experiments using a similar behavioral paradigm (Gao et al. 2011), guided by our prior experience fitting similar models to such data sets. In the end, we specified the following priors:
Because it was not clear how to connect stimulus information processing from each of the two unisensory stimulus conditions, each of the models posses an independent set of parameters for the visual and auditory conditions.
Choice probabilities from the experiment. The rows indicate a particular subject’s performance, whereas the columns represent the modality conditions. Choice probabilities are framed as the probability of “rightward shift” endorsement. The data from the 2, 1, -1, and -2 pixel shift conditions are show as the blue, green, red, and black lines, respectively. In each panel, the point of indifference is shown as the dashed horizontal line
In addition, the SFW model possesses one additional free parameter α that weights the contribution of the auditory and visual stimulus modalities. As mentioned, α is bound by zero and one, which can sometimes cause instabilities in the estimation procedure. We applied a logit transformation to α for reasons similar to the logarithmic transformation above, and specified the prior on this transformed space:
where
This particular prior was chosen because it places approximately equal weight for all values of α in the unit interval (i.e., the probability space), and as a consequence, it allows us to be agnostic about the relative contributions of auditory and visual stimulus cues in the bimodal stimulus condition.
Experiment
We now present the details of our experiment. Recall that our goal is to understand how the multimodal integration process occurs over time. To do this, we manipulated two important variables in our interrogation paradigm. First, we manipulated the type of information that was presented to the subject: auditory alone, visual alone, or auditory and visual together. Second, we manipulated the time that the stimulus was present before requiring a response. Together, these components provide insight into how the representations are fused together in the crucial bimodal condition.
Subjects
Six subjects with normal hearing and normal or corrected-to-normal vision completed 420 trials in each of the auditory, visual and combined conditions in each of 12-20 sessions, which allowed enough data for detailed assessment of each subjects’ performance. Subjects gave their informed consent, and were told that they would be paid USD $5.00 plus an additional amount determined by their performance for their participation in each session. For every point earned, subjects were paid an additional USD $0.01. To improve retention, subjects received a“completion bonus” of $4 per session for participating in all the required sessions.
Stimuli and apparatus
For each trial, subjects saw a fixation cross at the center of the screen paired with an auditory sound signaling the beginning of the trial, and the stimulus was displayed 500ms later. In the visual-only condition, the stimulus was a rectangle, drawn by an outline 1px wide. The rectangle was 300px wide and 100px high. On each trial, the rectangle stimulus was shifted to either the left or the right by 1 or 2 pixels. In the auditory-only condition, the stimulus was white noise played to either ear at two different intensity levels. The two levels of white noise intensity were obtained by setting the volumes of the two headphone channels as V1 = V0(1 + d×S) and V2 = V0(1−d×S) through PsychToolBox, where S takes value of 1 or 2 representing the two auditory intensity levels, and d represents the base difference. The base difference d was adaptively chosen for each individual subject at the beginning of the experiment so that their stimulus sensitivity to the visual shifts and auditory shifts were approximately the same. In the combined stimulus condition, the stimulus was always a visual stimulus and a congruent auditory stimulus, both shifted by the same number of unit steps (one or two) in the same direction.
The visual cues of this experiment were displayed on a 17 inch Dell LCD monitor at 1280 x 1024 resolution. All visual cues were light gray on a darker gray background. Auditory cues were played through Beyerdynamic DT150 headphones. The experiment was run using the Psychophysics Toolbox v3 extensions of Matlab R2010b. Auditory control with precise timing was obtained using M-Audio 1010LT audio card. Subjects were seated approximately 2.5 feet from the computer monitor in the experiment. Subjects were instructed to report the direction of the shift by pressing one of two buttons on the keyboard, the “z” button for left shifts and the “?/” button for right shifts.
Procedure
Subjects performed a two-alternative forced decision task similar to that used in many multisensory integration studies. Three types of trials were used: auditory trials, visual trials, and combined trials. The first 2-5 sessions were training sessions in which the physical auditory stimulus levels were adaptively adjusted so that subjects’ sensitivity in the visual and auditory conditions were approximately the same. The adapted auditory stimulus was then used for each of the following sessions.
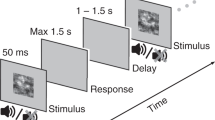
Subjects were instructed to hold their response until receiving a go cue. On each trial, a fixation point appeared at the start of the trial, and 500 msec later, the stimulus presentation began. At different delays after stimulus onset (75, 150, 300, 450, 600, 1200, and 2000 msec), the stimulus presentation ended, and a go cue was presented. The go cue consisted of an auditory tone accompanied by the presentation of the word “GO!” in the middle of the display screen. Subjects pressed one of two response keys to indicate their judgment about whether the stimulus was located to the left or right of center. Subjects were to respond within 300 msec after go cue onset and received feedback on each trial 750ms after the go cue.
Visual and auditory feedback was used to indicate to the subject whether the response occurred within the 300ms response window, and (if so) whether it was correct. If subjects responded within the response window and chose correctly, they received one point for the trial, feedback consisting of a pleasant noise, and a display with the total number of accumulated points on the screen. Incorrect, early, or late responses earned no points, and the feedback was an unpleasant noise with visual feedback of “X,” “Too early,” or “Too late” on the screen, respectively. The total time allotted for feedback of any type was 500ms.
Results
We now present the results of our analysis in five stages. First, we discuss the raw behavioral data because, as we mentioned, multimodal integration experiments have not been reported with an interrogation paradigm. Second, we discuss our results in terms of discriminability as measured by signal detection theory model, and compare these discriminability measures to ones derived from assuming optimal integration. Third, we present the results of our three model variants, showing model fits and model comparison statistics. Fourth, we examine the estimated posterior distribution of the α parameters in our SFW model and compare them to the optimal setting of α, determined by unimodal feature reliability. Finally, we discuss differences across the two modalities in the values of the time offset parameter τ and the three variability parameters σ b , σ w , and σ 0 and consider how these relate to differences in the time-accuracy curves for the two modalities.
Raw data
We begin our analysis by examining the raw choice probabilities for each modality by shift condition. Figure 2 shows the choice probabilities for each subject (rows) by modality (columns) condition. The choice probabilities are framed as the probability of endorsing the “rightward shift” alternative. The blue, green, red, and black lines represent the choice probabilities for the 2, 1, -1, and -2 pixel shift conditions, respectively, across each of the 7 go cue delay conditions. In each panel, the point of indifference (i.e., the point at which each response alternative is equally preferred) is shown as the dashed horizontal line.
Although Fig. 2 shows large individual differences in the choice probabilities, some features of the data remain consistent across subjects. First, the larger pixel shift conditions result in higher choice probabilities toward the correct alternative, relative to the lower pixel shift conditions. Specifically, the blue and black lines – which represent the 2 and -2 pixel shift conditions, respectively – are farther from the point of indifference (0.5) than either the green or red lines – which represent the 1 and -1 pixel shift conditions, respectively. A second general trend in the data is that the choice probabilities tend to become more discriminable (i.e., move away from the point of indifference) as the go cue delay increases. The standard interpretation of the gradual increase in discriminability is that the cumulative sum of the noisy perceptual samples contains more signal relative to noise over time. Analogously, the ADM presented below describes how the average of these samples has a higher signal-to-noise ratio, allowing the representation of the stimulus to be more discriminable over time.
Some features of the data are not consistent across subjects. For example, at the shortest go cue delay condition, we see that not all subjects begin at the point of indifference. This property suggests that some subjects (e.g., Subjects hh and la) begin with an initial (rightward choice) bias for reasons that are unlikely to be a consequence of the stimuli. Another clear individual difference in the data is the maximum level of response probability for the alternatives. For example, Subject mb never reaches a response probability of 0.8 for the rightward choices under any go cue delay, whereas Subject hh reaches much more extreme choice probabilities for even the shorter go cue delay conditions (e.g., a probability of 0.9 at go cue delay 0.6). The rate of response endorsement for each alternative will be more carefully examined in the next section.
Discriminability analysis and optimality
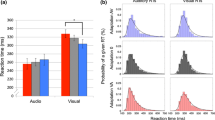
Rather than examining the probability of response endorsement, we can rely on summary statistics that characterize the level of discriminability for a particular condition. To do this across the four stimulus difficulty conditions, we assumed the presence of four Gaussian distributions, each centered at the location of the pixel shift conditions [−2,−1,1,2]. We then assumed that each Gaussian distribution had a standard deviation parameter equal to σ d , and a single decision criterion parameter was used as in the traditional signal detection theory model (Balakrishnan and MacDonald 2001). We then freely estimated σ d and the decision criterion for each subject at each interrogation time. Given these assumptions, the level of discriminability for the one-pixel shift condition is \(d^{\prime }=2/\sigma _{d}\), whereas discriminability in the two-pixel shift condition is \(d^{\prime }=4/\sigma _{d}\). Figure 3 shows the calculated \(d^{\prime }\) values for each subject (shown as panels) in the two-pixel shift condition. The green, red, and blue lines represent the \(d^{\prime }\) curves for the auditory, visual, and both conditions, respectively, across all go cue delays. The general pattern across subjects – echoed from Fig. 2 – is that \(d^{\prime }\) increases as a function of the go cue delay.
Discriminability-based optimality analysis from the experiment. The data from the visual, auditory, and bimodal conditions (two-pixel shift stimuli only) are show as the red, green and solid black lines, respectively. The performance of the optimal integration model is shown as the dashed black lines
We can also examine the subjects’ performance relative to the optimal integration model discussed above. Letting \({d^{\prime }}_{v}\) and \({d^{\prime }}_{a}\) denote the discriminability from the visual and auditory conditions, respectively, the discriminability for the both condition \({d^{\prime }}_{b}\) under the assumptions of the optimal integration model is
Figure 3 shows the optimal observer’s \(d^{\prime }\) as the dashed black line. In the figure, deviations from optimal integration are shown as differences between the black and blue lines. For the majority of the subjects, the two curves are reasonably close to one another. However, for Subjects mb and ms, there are clear signs of suboptimal integration of the stimulus cues. The analysis in this section is somewhat crude, relying on differences in the \(d^{\prime }\) statistic that are less interpretable than what could be realized within a computational modeling framework. Specifically, the analysis in this section only informs our understanding of the accuracy of the integration process, but says nothing about how the auditory and visual cues are being integrated to form a representation in the bimodal condition. Considering these limitations, we will explore the results of fits of the models discussed above in the next section.
Model comparison and fit
To evaluate the relative merits of the three proposed ways of integrating sensory stimuli, we fit the three models to the data from our experimental task. To fit the models to the data, we used differential evolution with Markov chain Monte Carlo (DE-MCMC; ter Braak 2006; Turner et al. 2013) to estimate the shape of the joint posterior distribution, for each subject independently. We used 24 chains and obtained 5,000 samples after a burn-in period of 1,000 samples. The burn-in period allowed us to converge quickly to the high-density regions of the posterior distribution, while the rest of the samples allowed us to improve the reliability of the estimates. Visual inspection of each chain was used to assure us that the chains had converged. Following the sampling process, we thinned the chains to reduce autocorrelation by retaining every other sample. Thus, our estimates of the joint posterior distribution for each model are based on 60,024 samples.
To compare the three models on the basis of model fit, we used the Watanabe-Akaike information criterion (WAIC; Watanabe 2010).Footnote 2 For this statistic, a lower value indicates a better model fit to the data. Table 2 shows the resulting WAIC values obtained for each model (columns) by subject (rows) combination. Table 2 shows that for Subjects am and la, the Adaptive Optimal Weights model provided the best fit, whereas for the remaining subjects the Static Free Weights model provided the best fit.
We can also visually examine the fit of the model predictions relative to the data. In this section, we show the model fits in terms of discriminability for visual clarity, but Fig. 7 shows the model predictions for response probabilities against the raw data as in Fig. 3. Figure 4 shows the discriminability data from the experiment for each subject in the auditory, visual, and bimodal conditions as the green, red, and blue lines, respectively. Figure 4 also shows the predictions of the corresponding best-fitting model for each subject. To generate predictions from the model, we randomly sampled values for the parameters from the estimated joint posterior distribution, and then simulated data from the model with those samples. We then calculated the median and 95 % credible set of the simulated data. In Fig. 4, the medians are shown as the dashed lines, and the 95 % credible sets are shown as the shaded regions with corresponding colors. In general, we see that the best-fitting model tends to make predictions that are consistent with the data. Furthermore, we see that the models are sensitive to noisy data, and account for this additional noise by inflating the 95 % credible set. For example, the credible sets for Subject hh are dispersed, whereas the credible sets for Subject am, whose data were also best captured by the AOW model, are considerably more narrow.
Posterior predictive distributions from the best fitting model against the data from the experiment. The data from the auditory, visual, and bimodal conditions are show as the green, red, and blue lines, respectively. The predictions from the best fitting model for each subject are shown as the dashed lines (median prediction) along with the 95 % credible set (shaded regions) with corresponding colors
Optimality of modality weights
For our next investigation, we assessed the degree of optimality for the modality weights in the SFW model for the four participants whose data were best fit by the SFW model – that is, all of the participants other than am and la (Table 2). We hypothesized that the posterior distribution of the modality weight parameter α might explain why these four subjects’ data were more consistent with the SFW model than the SOW model. Specifically, we suspected that there may be some departure in the estimates of α considered optimal by the SOW model from the estimates obtained when freely estimating α, as in the SFW model.
To examine our hypothesis, we first plotted the posterior distribution of the weight parameter α for the SFW model. Figure 5 shows the 95 % credible set across time as the blue shaded area for each participant, though the comparisons are not as relevant for Subjects am and la because their data were best fit by the AOW model. To provide a reference of the optimal setting for α, we used the internal calculations for the SOW model (see Eq. 12) to calculate α ∗ for each subject. These estimates, despite being a deterministic function of the model parameters, have some inherent variability as a result of generating the estimates through the posterior predictive distribution (i.e., because the posterior estimates for the model parameters have uncertainty within them). Figure 5 shows the 95 % credible set for these optimal estimates from the SOW model as the green shaded area across time. Finally, we also calculated estimates for the weights derived from the AOW model. For this model, the degree to which the visual or auditory information should be attended depends on the nondecision time parameter τ as well as the relative values of the three σ parameters within each modality, and as a consequence, the weights change across time. Figure 5 shows the 95 % credible set of weights expected for the AOW model as the red shaded area, generated from the posterior predictive distribution. For all subjects except Subject jl, the distribution of weights suggest that the optimal weighting strategy is to first attend to the auditory modality, with a gradual adjustment toward a more balanced allocation of attention as time increases.
Estimated posterior distributions for the modality weights α in the SFW model (blue), the SOW model (green), and the AOW model (red) for each of the six subjects. The bands represent the 95 % credible set for each model. Recall that in the SFW model, α was freely estimated, whereas in the SOW and AOW models, α was determined by the representations used in the auditory and visual conditions
Figure 5 shows that the estimates for α from the SFW and SOW models diverge considerably for all participants other than am and la. That is, the posterior distributions for α from these two models show hardly any overlap. This suggests that these subjects are setting their weight parameters in a static way, but are not doing so in an optimal fashion. We will save further consideration of these participants’ weighting parameters for the General Discussion.
Differences in evidence integration delay across modalities
In this section, we consider possible differences in the evidence integration delay across the two stimulus modalities used in our experiment. The τ parameter for each of the two modalities reflects the difference between the evidence integration delay and the decision delay. Under the assumption that the decision delay is constant across all conditions of the experiment, comparing the nondecision time parameter τ across the two stimulus modalities allows us to estimate the difference in the evidence integration delay for auditory and visual information. We are aware that the conditions of our experiment would allow participants to adopt different decision delays in different conditions of the experiment. Thus, the interpretation of the results presented in this section must be tentative given this possibility. Given that the same response signal cue was used in all conditions, we considered the assumption sufficiently plausible to make the comparison potentially interesting.
Figure 6 shows the difference between the posterior distributions for τ v and τ a for each subject (see Table 5 for posterior credible sets for these parameters). The estimates shown are derived from the best-fitting model corresponding to each subject. To examine these posteriors, we simply examine the posteriors relative to the point at which τ v = τ a . As a reference, a dashed vertical line appears in each panel that corresponds to this location. If the tau parameter for the visual condition is greater than that of the auditory condition, τ v will be larger than τ a and consequently, we will see a larger portion of the posterior to the right of the vertical line. Figure 6 shows that for every subject except Subject jl, τ v >τ a , consistent with the conclusion that the evidence integration delay is generally greater for visual than for auditory information. For most subjects, this parameter difference is substantial (e.g., p(τ v >τ a )=1.0 for Subjects mb, am, and hh), although for Subject jl, the evidence that the auditory nondecision time parameter is larger that the visual nondecision time parameter is relatively weak – in fact, in the opposite direction – such that p(τ v <τ a )=0.54.
A comparison across modalities of the estimated posterior distribution for the nondecision time parameter τ. Each panel shows the difference in τ between visual and auditory stimulus modalities for the best fitting model for each subject. Reference lines appear in each panel for the point at which the two nondecision time parameters are equal. The units of τ are in seconds
As noted at the beginning of this section, it seems reasonable to treat the differences in the τ parameter across modalities shown in Fig. 6 as reflecting modality-specific differences in the time required for stimulus encoding. Assuming this, our data support the conclusion that stimulus encoding time is generally shorter for the auditory than the visual modality. Figure 6 shows that for every subject except Subject jl, τ v >τ a , suggesting that the visual stimulus information takes longer to encode than does auditory information. This pattern of results is consistent with other studies. For example, Bell et al. (2005) found that in a congruent stimulus presentation (i.e., both auditory and visual information was consistent with respect to direction), the response to the auditory features of the stimuli came before that of the response to the visual features. Although this particular finding came from single-unit recordings of the superior colliculus of primates, our results corroborate the result in humans.
Variance parameters, asymptotic accuracy, and the shapes of time-accuracy curves
Summaries of the posterior distributions for the three types of variance parameters appear in the Appendix (Table 3). These parameters are worth examining because they explain the behavioral performance in the two unimodal conditions by means of three different types of noise: starting point variability, between-trial variability, and within-trial variability. The easiest parameters to interpret and relate to data are the between-trial variability parameters σ b . As shown in Eq. 4, performance is inversely related to σ b , which means that the subjects with higher values of σ b should have lower asymptotic d ′ curves. Figures 3 and 4 show that this is indeed the case. As the most extreme example, Subject la has estimates of σ b that range from (0.357,0.442) for the auditory modality, and (0.447,0.611) for visual modality. From these values and Eq. 4, we should expect the \(d^{\prime }\) curve for the auditory modality to be larger than the visual modality curve. Figure 3 confirms this prediction, where the auditory \(d^{\prime }\) curve (green) levels off at a higher value than the visual \(d^{\prime }\) curve (red). The other parameters σ 0 and σ w together affect the rate of growth in the \(d^{\prime }\) curves. There are clearly differences in rate of evidence accumulation across modalities for some partipants, and these appear to be well-captured by the model. In particular, both am and la show much more rapid growth of \(d^{\prime }\) in the auditory than the visual modality, and this is well captured by the model fits as shown in Fig. 4.
Discussion
In this article, we have joined two important lines of research on the study of multimodal perceptual decision making. The first deals with how observers integrate sources of information that have different sensory properties. The second deals with how evidence for a choice is accumulated over time. We presented data from a multimodal integration task within the interrogation paradigm, which allowed us to study how the process of sensory modality integration occurs over time. Our experimental design facilitated a comparison across stimulus modalities, and the models we used allowed us to compare stimulus processing relative to theories of optimality. In this section, we discuss some of the features of our models in greater detail, as well as addressing some important limitations of our results.
Comparing the averaging diffusion model to the drift diffusion model
We do not see the ADM as being at odds with the DDM. In this article, the ADM was proposed as a way of investigating the time course of integrating multiple streams of information into a single representation of the environment in a way that connects with existing literature in the field of multimodal integration (Landy et al. 2011). Formally, the ADM and DDM are almost notational variants of one another in the absence of a decision bound. As we discussed in the introduction, both the mean and standard deviation of the evidence variable in the DDM are simply divided by t to obtain the mean and standard deviation of the evidence variable in the ADM. As a consequence, when diving the mean by the standard deviation, as one would when calculating the signal-to-noise ratio, the resulting \(d^{\prime }\) measures are identical across the two models because \(d^{\prime }(t)\) is proportional to μ(t)/σ(t) (see Eqs. 2 and 4).
The advantage of developing the ADM is that it can be extended to task in which participants are asked to indicate their estimate of the position of the stimulus on a continuum, as reflected in the ADM’s evidence variable a(t). Such extensions are in line with recent developments of the DDM for continuous elicitation paradigms (Smith 2016).
Our experiment used an exogenous stopping rule via the interrogation paradigm where subjects were required to respond immediately following a go cue. While this paradigm is useful in understanding how the sensory variables evolve over time, as presented here, the model is not suited for endogenous stopping rules where subjects determine when a choice should be made. These paradigms, often referred to as “free response” paradigms, are conceptually quite similar to interrogation paradigms, but models of this task require some mechanism to terminate the information accumulation process. Typically, the termination process is instantiated in a decision model such as the DDM through a response threshold parameter. Although it has been argued that a response threshold mechanism could underly the decision dynamics in the interrogation paradigm (see Ratcliff 2006), we have ignored this possibility here because excellent fits to time-accuracy curves are often obtained without such a mechanism (see, e.g., Gao et al. 2011, for a study that used a procedure very similar to the one used here). Because including the possibility of an early termination policy (i.e., prior to the go cue) would greatly increase the complexity of the ADM presented here, we opted for the simpler formulation in which the decision variable remains continuous until readout is triggered by the go cue. Future work could investigate ‘the incorporation of a decision bound into’ the ADM.
Weight parameters, optimality, and neglect
One surprising result from our analyses was the lack of optimality in the decision making process for four out of our six subjects. Recall that we used two different definitions of optimality when constructing variants of ADM. First, we used the classic definition of optimality where weights are established on the basis of the variability (i.e., reliability) of the unimodal sensory stimuli. This computation assumed by the Adaptive Optimal Weights (AOW) model, is shown in Eqs. 6 and 7. According to this model, at each instant in time, the weight assigned to the input from each stimulus modality is determined by its relative reliability. We explained that as the reliability of one sensory modality increased, the weight assigned to that sensory modality in the bimodal condition would also increase. As the name suggests, this version of the model is “adaptive” meaning that this assessment of reliability is done dynamically at each point in time. Second, we considered another form of optimality on the basis of overall accuracy. This model, which we called the Static Optimal Weights (SOW) model, is similar to the AOW model in the sense that the SOW model has weights that are completely determined by a particular strategy for optimization. However, the SOW model is different in that it is “static” over time: the optimization of the model weights is done for all time points simultaneously. The combination of these two models allows us to address the question of how optimization is performed – either dynamic or static – if optimization is performed at all. After fitting our models to data, we determined that optimization was the best account of the data for Subjects am and la, and the type of optimization used was adaptive, not static (See Table 2).
Another way of assessing the degree of optimality on a more continuous basis is through the Static Free Weights (SFW) model. In this variant, we assumed no specific strategy for cue integration as defined by optimality, but instead allowed the cue integration to be inferred by way of the parameter α. Hence, the parameter α carries with it useful information about both the degree of optimality, because we can directly compare the estimates of α with the calculations of optimality assumed by the SOW models. A comparison of the estimates of α to the AOW model is less straightforward as these weights adjust across time. Figure 5 shows that, for the four participants who were better fit by the SFW model, the estimates for α obtained by the SFW model rarely have density in areas that would be considered optimal by the SOW model.
The estimates of α can also be used to assess whether any sort of integration occurred. Unlike other parameters in the model, the α parameter is most directly informed by data in the bimodal condition. As a consequence, α can be interpreted directly as it applies to integrating the two cues. Because the α parameter reveals the weight assigned to each stimulus modality, when an estimate of α is near either bound (i.e., near zero or one), we can conclude that only one source of information was used in the bimodal condition. Specifically, when α is near 1, only the visual information in the bimodal condition was used, whereas when α is near 0, only the auditory information was used. As α tends toward 0.5, it suggests that the subject is using some combination of both cues – whether it be optimal or not – to form a representation of the stimulus in the bimodal condition. Of the four participants best fit by the SFW model, subjects hh, jl, and mb appear to use both stimulus modalities in the bimodal condition, whils subject ms appears to use a different strategy. Specifically, subject ms appears to rely almost exclusively on the auditory cue. This strategy of neglecting the visual information may be a fairly reasonable one for this participant. According to the SOW model, the optimal weight setting is 0.28, and this makes sense because the participant’s d’ scores are higher at all time points in the auditory than the visual modality. Thus, although overweighting the auditory modality has a cost, it is far better than overweighting the visual modality. Figure 4 hints at the same aspect of the decision making through the \(d^{\prime }\) curves. That is, the \(d^{\prime }\) curve for the bimodal condition is very similar to the \(d^{\prime }\) curve in the auditory modality for Subject ms.
There is one other participant, mb, whose \(d^{\prime }\) data in Fig. 3 also appears consistent with placing all of the weight on one dimension – in this case the visual dimension – in the bimodal condition. That is, for this participant, the \(d^{\prime }\) curve shown for the both condition lies nearly exactly on top of the \(d^{\prime }\) curve for the visual condition, and for this participant, \(d^{\prime }\) for visual is better at all time points than \(d^{\prime }\) for auditory, so that choosing to rely on the visual input only may be somewhat reasonable for this participant. However, the model provided an alternative account for this pattern of data, in which the participant is treated as placing more of the weight on the auditory input than the visual input. This solution may have been found by the fitting process because it can account for the fact that the initial bias in the both condition is a compromise between the bias in the auditory and visual conditions. Whether this is indeed what the participant was doing or whether, instead, the participant used a visual-only strategy in the both condition but adopted a different bias than in the visual condition cannot be determined from our data.
Finally, we briefly discuss two other participants, hh and jl, whose performance in the both condition was not markedly sub-optimal in terms of the \(d^{\prime }\) analysis, but for whom the model found that the best-fitting static weight was not the same as the optimal static weight for either participant. These findings can be understood by noting that moderate deviations from optimal weighting – especially of nearly-equally reliable cues – is not terribly costly in the \(d^{\prime }\) measure. As an example, when the reliabilities of the two cues are exactly equal, so that \(d^{\prime }\) for each modality would be the same, the optimal weighting (.5) produces a \(d^{\prime }\) equal to 1.41 times the \(d^{\prime }\) for either modality, whereas a weighting of .333 or .667 (i.e., placing twice the weight on one rather than the other modality) produces a \(d^{\prime }\) equal to 1.34, only about 5 % smaller than the optimal \(d^{\prime }\).
Artificial vs. realistic cues
Given that some subjects in our experiment exhibited patterns of results that are inconsistent with optimal cue integration it is worth speculating about the reason for this suboptimality, particularly for participants mb and ms, where the deviations from optimality are fairly substantial. One potential explanation is the lack of realistic cues used in our experiment. While the laboratory setting allows for control over stimuli by the experimenter, the results may not correlate perfectly with the function of the human nervous system in a natural environment. Human perceptual systems are designed to perform tasks useful for survival in the environment in which they evolved. The artificial nature and the scarcity of sensory cues in a laboratory present an issue in the sense that they could place a subject in a situation that their nervous system is ill equipped to manage, and as a result, they may perform suboptimally (Landy et al. 2011). Specifically, Buckley and Frisby (1993) had observers make depth judgements while viewing ridges in artificial and realistic stimulus conditions. In the realistic stimulus condition, actual three-dimensional ridges were made of a textured card on a wooden form. In the artificial condition, the shading of lines on a computer screen gave the impression of raised ridges on a similar-looking wooden form. When comparing the performance across conditions, Buckley and Frisby (1993) found a significant improvement of the subjects’ ability to perceive depth in the real ridge experiment compared to the artificial images. While the limitations of artificial and realistic cues is an important consideration, Landy et al. (2011) provide an in-depth discussion arguing that, when fitted to cue integration data, some Bayesian models largely correct for the artificial nature of the cues.
The discrepancy between realistic and artificial cues can also be realized in the auditory domain. For example, in real world scenarios, humans use the interaural time differences present in auditory stimuli to better triangulate the position from which a sound originated (for a review see Blauert 1983). Although our study was limited because we did not manipulate interaural time differences, such manipulations have been used in auditory perception tasks (Meyer and Wuerger 2001; Wuerger et al. 2003; Alais and Burr 2004). While we do feel that interaural time differences are an important consideration in location orientation, these variables can be very difficult to control in the laboratory. Furthermore, Landy et al. (2011) argued that relative to visual discrepancies between artificial and realistic cues, the differences in auditory discrepancies are less severe. On the other hand, the variable we did manipulate was loudness, which has been shown to be an effective indicator of the stimulus position (e.g., Blauert 1983). Indeed, our results demonstrate that the manipulation of loudness was sufficient for some of our subjects to integrate the auditory and visual cues, which suggests that the auditory cues are at least somewhat realistic. With such cues, it may be that some participants are able to integrate the cues, and some are not. In our case, it appears that am, hh, jl, and la should be counted among the integrators, while ms should not; as discussed above, it is difficult to be sure whether mb was an integrator or not.
Conclusions
In this article, we have explored how the process of multimodal stimulus integration unfolds over time. We developed the Averaging Diffusion Model as a way to combine standard theories of evidence accumulation with standard theories of multi-modal information integration. We proposed three different forms of cross-modal integration, which were chosen to directly assess the optimality of the integration process. We found that basing modality weights on the relative reliability of the stimulus at each time point during evidence integration was the most likely strategy for two of our subjects (Subjects am and la). However, a model assuming a completely free strategy of modality weight setting provided the best account of four subjects in our data (Subjects jl, hh, mb, and ms). This model had one more parameter than either optimal integration model, but still provided a better fit after penalty terms were applied for model complexity. Our results highlight the importance of studying the modality integration process over time, and suggest that, under the conditions of our experiment at least, evidence integration across modalities approaches optimality for some but not all participants.
Notes
Note that neither the encoding delay nor the decision delay are directly observed, because the response occurs after a further response activation process whose duration may depend on the state of the continuous decision variable at the time this process is initiated (Gao and McClelland 2013).
The Bayesian predictive information criterion (BPIC; Tomohiro 2007) provided identical conclusions as the WAIC.
References
Alais, D., & Burr, D. (2004). The ventriloquist effect results from near-optimal bimodal integration. Current Biology, 14, 257–262.
Angelaki, D. E., Gu, Y., & DeAngelis, G. C. (2009a). Multisensory integration: psychophysics, neurophysiology, and computation. Current Opinion in Neurobiology, 19, 452–458.
Angelaki, D. E., Klier, E. M., & Snyder, E. H. (2009b). A vestibular sensation: probabilistic approaches to spatial perception. Neuron, 64, 448–461.
Balakrishnan, J., & MacDonald, J. (2001). Alternatives, misrepresentations of signal detection theory and an alternative approach to human image classification. Journal of Electronic Imaging, 10, 376–384.
Battaglia, P. W., Jacobs, R. A., & Aslin, R. N. (2003). Bayesian integration of visual and auditory signals for spatial localization. Journal of the Optical Society of America, 20, 1391–1397.
Bejjanki, V. R., Clayards, M., Knill, D. C., & Aslin, R. N. (2011). Cue integration in categorical tasks: Insights from audio-visual speech perception. PloS One, 6, 1–12.
Bell, A., Meredith, A., Van Opstal, A. J., & Munoz, D. P. (2005). Crossmodal integration in the primate superior colliculus underlying the preparation and initiation of saccadic eye movements. Journal of Neurophysiology, 93, 3659–3673.
Benjamin, A. S., Diaz, M., & Wee, S. (2009). Signal detection with criterior noise: Applications to recognition memory. Psychological Review, 116, 84–115.
Blauert, J. (Ed.) (1983). Spatial Hearing. Cambridge: MIT Press.
Bresciani, J. -P., Dammeier, F., & Ernst, M. O. (2008). Tri-modal integration of visual, tactile, and auditory signals for the perception of sequences of events. Brain Research Bulletin, 75, 753–760.
Brown, S., & Heathcote, A. (2005). A ballistic model of choice response time. Psychological Review, 112, 117–128.
Brown, S., & Heathcote, A. (2008). The simplest complete model of choice reaction time: Linear ballistic accumulation. Cognitive Psychology, 57, 153–178.
Buckley, D., & Frisby, J. P. (1993). Interaction of stereo, texture and outline cues in the shape perception of three-dimensional ridges. Vision Research, 33, 919–933.
Burr, D., Silva, O., Cicchini, G. M., Banks, M. S., & Morrone, M. C. (2009). Temporal mechanisms of multimodal binding. Proceedings in Biological Sciences / The Royal Society, 276, 1761– 1769.
Colonius, H., & Diederich, A. (2010). The optimal time window of visual-auditory integration: a reaction time analysis. Frontiers in Integrative Neuroscience, 4, 1–11.
Ditterich, J. (2010). A comparison between mechanisms of multi-alternative perceptual decision making: Ability to explain human behavior, predictions for neurophysiology, and relationship with decision theory. Frontiers in Neuroscience, 4, 184.
Driver, J., & Noesselt, T. (2008). Multisensory interplay reveals crossmodal influences on sensory specific brain regions, neural responses, and judgments. Neuron, 57, 11–23.
Drugowitsch, J., Pouget, A., DeAngelis, D. C., & Angelaki, D. E. (2015). Tuning the speed-accuracy trade-off to maximize reward rate in multisensory decision-making. eLife 4.
Ernst, M. O., & Banks, M. S. (2002). Humans integrate visual and haptic information in a statistically optimal fashion. Nature, 415, 429–433.
Fetsch, C. R., Pouget, A., DeAngelis, G. C., & Angelaki, D. E. (2011). Neural correlates of reliability-based cue weighting during multisensory integration. Nature Neuroscience, 15, 146–154.
Fetsch, C. R., Turner, A. H., DeAngelis, G. C., & Angelaki, D. E. (2009). Dynamic reweighting of visual and vestibular cues during self-motion perception. Journal of Neuroscience, 29, 15601–15612.
Forstmann, B. U., Ratcliff, R., & Wagenmakers, E. -J. (2016). Sequential sampling models in cognitive neuroscience: advantages, applications, and extensions. Annual Review of Psychology, 67, 641–666.
Gao, J., & McClelland, J. L. (2013). Continuous decision states and their translation into action, unpublished article, Stanford University.
Gao, J., Tortell, R., & McClelland, J. L. (2011). Dynamic integration of reward and stimulus information in perceptual decision-making. PLoS ONE, 6, 1–21.
Gelman, A., Carlin, J. B., Stern, H. S., & Rubin, D. B. (2004). Bayesian data analysis. New York: Chapman and Hall.
Gu, Y., Angelaki, D. E., & Deangelis, G. C. (2008). Neural correlates of multisensory cue integration in macaque MSTd. Nature Neuroscience, 11, 1201–1210.
Jay, M., & Sparks, D. (1984). Auditory receptive fields in primate superior colliculus shift with changes in eye position. Nature, 309, 345–347.
Kiani, R., Hanks, T. D., & Shadlen, M. N. (2008). Bounded integration in parietal cortex underlies decisions even when viewing duration is dictated by the environment. Journal of Neuroscience, 28, 3017–3029.
Kiefer, A. W., Riley, M. A., Shockley, K., Villard, S., & Van Orden, G. C. (2009). Walking changes the dynamics of cognitive estimates of time intervals. Journal of Experimental Psychology: Human Perception and Performance, 35, 1532–1541.
Knill, D. (1998). Discrimination of planar surface slant from texture: Human 1208 and ideal observers compared. Vision Research, 38, 1683–1697.
Laming, D. R. (1968). Information theory of choice reaction time. New York: Wiley Press.
Landy, M. S., Banks, M. S., & Knill, D. C. (2011). Ideal-observer models of cue integration Vol. 19. Oxford: Oxford University Press.
Ma, W. J., & Pouget, A. (2008). Linking neurons to behavior in multisensory perception: A computational review. Brain Research, 1242, 4–12.
Mazurek, M. E., Roitman, J. D., Ditterich, J., & Shadlen, M. N. (2003). A role for neural integrators in perceptual decision making. Cerebral Cortex, 13, 1257–1269.
McDonald, J. J., Teder-Slejrvi, W. A., & Hillyard, S. A. (2000). Involuntary orienting to sound improves visual perception. Nature, 407, 906–908.
Meredith, M., & Stein, B. (1983). Interactions among converging sensory inputs in the superior colliculus. Science, 221, 389–91.
Merkle, E. C., & Van Zandt, T. (2006). An application of the poisson race model to confidence calibration. Journal of Experimental Psychology: General, 135, 391–408.
Meyer, G. F., & Wuerger, S. M. (2001). Cross-modal integration of auditory and visual motion signals. NeuroReport, 12, 2557–2560.
Mueller, S. T., & Weidemann, C. T. (2008). Decision noise: an explanation for observed violations of signal detection theory. Psychonomic Bulletin and Review, 15, 465–494.
Mulder, M. J., Wagenmakers, E. -J., Ratcliff, R., Boekel, W., & Forstmann, B. U. (2012). Bias in the brain: a diffusion model analysis of prior probability and potential payoff. Journal of Neuroscience, 32, 2335–2343.
Noorbaloochi, S., Sharon, D., & McClelland, J. L. (2015). Payoff information biases a fast guess process in perceptual decision making under deadline pressure: Evidence from behavior, evoked potentials, and quantitative model comparison. Journal of Neuroscience, 35, 10989–11011.
Ohshiro, T., Angelaki, D. E., & DeAngelis, G. C. (2011). A norMalization model of multisensory integration. Nature Neuroscience, 14, 775–784.
Pouget, A., Deneve, S., & Duhamel, J. -R. (2002). A computational perspective on the neural basis of multisensory spatial representations. Nature Reviews Neuroscience, 3, 741–747.
Purcell, B., Heitz, R., Cohen, J., Schall, J., Logan, G., & Palmeri, T. (2010). Neurally-constrained modeling of perceptual decision making. Psychological Review, 117, 1113–1143.
Ratcliff, R. (1978). A theory of memory retrieval. Psychological Review, 85, 59–108.
Ratcliff, R. (2006). Modeling response signal and response time data. Cognitive Psychology, 53, 195–237.
Ratcliff, R., & McKoon, G. (2008). The diffusion decision model: Theory and data for two-choice decision tasks. Neural Computation, 20, 873–922.
Ratcliff, R., & Rouder, J. N. (1998). Modeling response times for two-choice decisions. Psychological Science, 9, 347–356.
Ratcliff, R., & Smith, P. L. (2004). A comparison of sequential sampling models for two-choice reaction time. Psychological Review, 111, 333–367.
Reddi, B. A. J., & Carpenter, R. H. S. (2000). The influence of urgency on decision time. Nature Neuroscience, 3, 827–830.
Rowland, B. A., Quessy, S., Stanford, T. R., & Stein, B. E. (2007). Multisensory integration shortens physiological response latencies. Journal of Neuroscience, 7, 5879–5884.
Schall, J. D. (2003). Neural correlates of decision processes: neural and mental chronometry. Current Opinion in Neurobiology, 12, 182–186.
Shadlen, M. N., & Newsome, W. T. (2001). Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. Journal of Neurophysiology, 86, 1916–1936.
Smith, P. L. (2016). Diffusion theory of decision making in continuous report. Psychological Review, 123, 425–451.
Spence, C., McDonald, J., & Driver, J. (2004). Exogenous spatial-cuing studies of human crossmodal attention and multisensory integration. Oxford: Oxford University Press.
ter Braak, C. J. F. (2006). A Markov chain Monte Carlo version of the genetic algorithm Differential Evolution: Easy Bayesian computing for real parameter spaces. Statistics and Computing, 16, 239–249.
Tomohiro, A. (2007). Bayesian predictive information criterion for the evaluation of hierarchical bayesian and empirical bayes models. Biometrika, 94, 443–458.
Treisman, M., & Williams, T. (1984). A theory of criterion setting with an application to sequential dependencies. Psychological Review, 91, 68–111.
Tsetsos, K., Gao, J., & McClelland, J. L. (2012). Using time-varying evidence to test models of decision dynamics: Bounded diffusion vs. the leaky competing accumulator model. Frontiers in Neuroscience, 6, 76–79.
Turner, B. M., Sederberg, P. B., Brown, S. D., & Steyvers, M. (2013). A method for efficiently sampling from distributions with correlated dimensions. Psychological Methods, 18, 368–384.
Turner, B. M., Van Zandt, T., & Brown, S. D. (2011). A dynamic, stimulus-driven model of signal detection. Psychological Review, 118, 583–613.
Usher, M., & McClelland, J. L. (2001). On the time course of perceptual choice: The leaky competing accumulator model. Psychological Review, 108, 550–592.
van Beers, R. J., Sittig, A. C., & Gon, J. J. (1999). Integration of proprioceptive and visual position-information: an experimentally supported model. Nature Neuroscience, 81, 1355–1364.
Van Zandt, T. (2000). ROC Curves and confidence judgments in recognition memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 26, 582–600.
Van Zandt, T., & Ratcliff, R. (1995). Statistical mimicking of reaction time distributions: Mixtures and parameter variability. Psychonomic Bulletin and Review, 2, 20–54.
Vickers, D. (1979). Decision processes in visual perception. New York: Academic Press.
Vickers, D., Burt, J., & Smith, P. (1985). Experimental paradigms emphasizing state or process limitations: I. Effects on speed-accuracy tradeoffs. Acta Psychologica, 59, 129–161.
Wagenmakers, E. J., & Brown, S. (2007). On the linear relation between the mean and the standard deviation of a response time distribution. Psychological Review, 114, 830–841.
Wallace, M. T., Wilkinson, L. K., & Stein, B. E. (1996). Representation and integration of multiple sensory inputs in the primate superior colliculus. Journal of Neurophysiology, 76, 1246– 1266.
Watanabe, S. (2010). Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. Journal of Machine Learning Research, 11, 3571–3594.
Wickelgren, W. A. (1977). Speed-accuracy tradeoff and information processing dynamics. Acta Psychologica, 41, 67–85.
Witten, I. B., & Knudsen, E. I. (2005). Why seeing is believing: Merging auditory and visual worlds. Neuron, 48, 489–496.
Wong, K. -F., & Wang, X. -J. (2006). A recurrent network mechanism of time integration in perceptual decisions. The Journal of Neuroscience, 26, 1314–1328.
Wuerger, S. M., Hofbauer, M., & Meyer, G. F. (2003). The integration of auditory and visual motion signals at threshold. Perception and Psychophysics, 65, 1188–1196.
Acknowledgments
This work was funded by the NIH (award number F32GM103288) and by the Air Force Research Laboratory (Grant FA9550-07-1-0537). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the article. The authors would like to thank Chris Donkin, Andrew Heathcote, and James Palestro for insightful comments that improved an earlier version of this article. Author contributions: JG conceived research; JG and JLM designed research; JG, BT, and JLM developed the alternative modeling approaches; BT conducted model fitting and comparison; BT lead the writing of the paper with contributions from JLM and JG and assistance from SK and DP.
Author information
Authors and Affiliations
Corresponding author
Additional information
Brandon M. Turner and Juan Gao contributed equally on this project.
Appendix
Appendix
Choice probabilities from the experiment with model fits. Each row corresponds to a particular subject, whereas each column corresponds to a modality condition. All choice probabilities are framed as the probability of “rightward shift” endorsement. The data from the 2, 1, -1, and -2 pixel shift conditions are shown as the blue, green, red, and black lines, respectively. The model predictions are shown in corresponding colors, where the shaded areas illustrate the 95 % credible set, and the dotted line illustrates the median prediction. In each panel, the point of indifference is shown as the dashed horizontal line
Rights and permissions
About this article
Cite this article
Turner, B.M., Gao, J., Koenig, S. et al. The dynamics of multimodal integration: The averaging diffusion model. Psychon Bull Rev 24, 1819–1843 (2017). https://doi.org/10.3758/s13423-017-1255-2
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13423-017-1255-2