Introduction

Presenting statistical information in the external format of natural frequencies improves Bayesian reasoning compared with single-event probabilities in traditional Bayesian textbook problems (e.g., Cosmides & Tooby, 1996; Gigerenzer & Hoffrage, 1995). The nature of the cognitive mechanism underpinning such facilitation has kindled an intense and on-going debate (e.g., Barbey & Sloman, 2007; Brase, 2008; Gigerenzer & Hoffrage, 1995; Girotto & Gonzalez, 2001; Lesage, Navarrete, & De Neys, 2013; Sirota, Kostovičová, & Vallée-Tourangeau, 2015; Sloman, Over, Slovak, & Stibel, 2003).

Natural frequencies—originally formulated by Kleiter (1994) who stressed their natural sampling structure, which makes the base-rate information redundant—offer a computationally simpler format than single-event probabilities. However, more controversially, whether or not computational simplicity is the only element contributing to the facilitative effect remains an open question. In fact, according to the ecological rationality account, the computational simplicity as well as the specificity of information inputs provided by naturally sampled frequencies (i.e., natural frequencies) together drive the facilitation (e.g., Brase, 2008; Cosmides & Tooby, 1996; Gigerenzer & Hoffrage, 1995). The human mind adapted to process natural frequencies—since they reflect the way the information has been encountered naturally during evolution—and therefore reasons better with them than with any other formats. In contrast, according to the nested-sets account, the partitive structure of the problem leads to its nested-sets representation and enables a computationally simple solution of the problem (e.g., Girotto & Gonzalez, 2001; Sloman et al., 2003; Tversky & Kahneman 1983): Any format that reveals adequately the same partitive structure of the statistical information as natural frequencies would cause facilitation.

To test these two accounts, Girotto and Gonzalez (2001, 2002) contrasted natural frequencies with an isomorphic format that does not feature frequencies, namely a chances format that expresses single-event probabilities with natural sampling structure (e.g., 10 chances out of 1,000 that a woman has cancer). The two formats yielded similar performance supporting the computational simplicity prediction of the nested-sets account (Girotto & Gonzalez, 2001). However, further evidence weakened this conclusion since the chances format did not facilitate Bayesian reasoning to the same extent as did natural frequencies (Brase, 2008); we term this discrepancy the format gap. Prior research failed to address the underlying mechanism of such a gap despite its theoretical significance. An explanation for the gap would likely unveil the additional facilitatory ingredient of natural frequencies.

Interpreting the format gap: the format and problem interpretation hypotheses

We propose two non-exclusive interpretations of the gap: the format and problem interpretation hypotheses. The first interpretation posits that the mental representation of the statistical format accounts for the format gap; hence, the format interpretation hypothesis. Some researchers asserted that chances with natural sampling are really just natural frequencies disguised as probabilities (e.g., Hoffrage, Gigerenzer, Krauss, & Martignon, 2002). The mental representation of chances as frequencies rather than as probabilities will facilitate reasoning because frequencies are easier to process, for example, they tap easily into a frequency coding mechanism (e.g., Brase, 2008). Therefore, any discrepancies in performance between the two formats should be explained through the representation of chances as frequencies.

The second interpretation posits that the mental representation of the problem type—for example, classified in terms of required mathematical operations—accounts for the format gap; hence, the problem interpretation hypothesis. Some have proposed that every mathematical word problem, such as a Bayesian textbook problem, activates corresponding information networks in memory that cue related mathematical operators to map out a path to solution (Kintsch, 1988; Kintsch & Greeno, 1985). Consequently, the superior performance of natural frequencies may occur because participants interpret the task as a problem to which set operations should be applied rather than as a problem featuring frequencies.

The two mechanisms proposed by the format interpretation and problem interpretation hypotheses reflect to some extent two theoretical accounts of Bayesian reasoning—the ecological rationality account and the nested-sets account—but, strictly speaking, are not necessarily mutually exclusive. A frequency-based mental representation can trigger a set representation of the problem and therefore affect performance or vice versa. Only the joint investigation of the two mechanisms can differentiate between the two theoretical accounts of Bayesian reasoning. According to some proponents of the nested-sets account, the problem set representation unveils the nested-sets structure of a problem and triggers appropriate operations employed to solve the problem (e.g., Sloman et al., 2003). Frequencies may induce set operations, which lead to increased performance; however, it is the set representation and not the frequency format per se that spurs the facilitation.

In contrast, according to some proponents of the ecological rationality account, the information structure and question format affect Bayesian reasoning through their frequency representation. For example, Brase (2008) asserted that the effect of question format found in Girotto and Gonzalez (2001) could be explained “… by the degree to which [it] elicits a frequency representation” (Brase, 2008, p. 287). This implies that a frequency mental representation is needed for facilitation, above and beyond the appropriate set representation of the problem. Therefore, we hypothesized that unique support for the problem interpretation hypothesis corroborates some versions of the nested-sets account, whereas unique support for the format interpretation hypothesis corroborates some versions of the ecological rationality account.

The present experiments

In this paper, we report three tests of the problem interpretation hypothesis and the format interpretation hypothesis in two parallel experiments. The first part of Experiment 1 (part A) tested both hypotheses by investigating the mediation pathways via the problem and format mental representations of the effect of statistical, external, format on Bayesian performance. The second part of Experiment 1 (part B) tested both hypotheses by investigating the mediation pathways via the problem and format mental representations of the transfer effect on Bayesian reasoning. That is, a transfer effect from the previous Bayesian problem featuring either chances or natural frequencies to a new (medical) problem featuring natural frequencies. Experiment 2 tested directly the problem representation processes: it tested the causal effect of the availability of set representations—induced by priming set or normalization operations—on Bayesian performance. It also tested the independence of these processes from those proposed in the format interpretation hypothesis by measuring the effect of priming on the format of mental representations.

The problem interpretation hypothesis would be fully supported only if the problem representations mediate the format gap and subsequent transfer effect, and affect performance by priming set-problem representations. The format interpretation hypothesis would be fully supported only if the format mental representations mediate the format gap and subsequent transfer effect, and if priming affects performance via the changes in the format mental representations.

Method

Participants and design

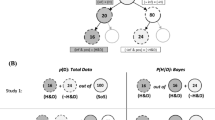
We aimed to include at least 82 participants in each of the two experiments, since we powered them to detect at least a medium size effect, w = 0.4 (a conservative estimate given the prior literature, e.g., Brase, 2008), when assuming α = .05, 1 – β = .95, and a two-sided test. Based on such power calculation, 169 social science undergraduates (45 males, age range 18–28 years, M = 20.6, SD = 1.4) from a national-level university in Slovakia participated in two parallel-design experiments (Fig. 1). In the first part of Experiment 1, designed to measure a format effect (part A), we allocated randomly the first (randomly selected) half of the participants (n = 84) to one of two format conditions featuring a Bayesian problem either in natural frequencies or chances. In the second part of Experiment 1, designed to assess a transfer effect (part B), the same participants (n = 84) answered a different (medical) Bayesian problem expressed in natural frequencies. In Experiment 2, designed to measure a priming effect, we allocated randomly the remaining participants (n = 85) to one of two priming conditions: priming normalization or priming sets. This priming manipulation prompted participants to perform either normalization- or set-related operations on structurally unrelated tasks before completing the critical Bayesian problem featuring chances.

Fig. 1
figure 1

Flowchart of the design and sample size of the two parallel experiments

Full size image

Materials and procedure

Participants in the first part of Experiment 1 (format effect) solved a Bayesian problem expressed either in chances or natural frequencies (namely, the “Admission” problem, as used in Brase, 2008; adopted from Girotto & Gonzalez, 2001; see both versions in Table 1). We coded the responses numerically corresponding to the Bayesian solution (i.e., 3 out of 22 chances/applicants) as Bayesian and the rest as non-Bayesian answers. Upon completion, participants assessed the ways they thought about the problem and format (i.e., the problem and format representations). The problem representation was measured by the operations reported by participants on a 7-point Likert scale [1: “I considered the solution to the task as one involving a transformation into percentages, probabilities or other normalizations (such as ‘to hundreds’)”; 4: “Both equally”; 7: “I considered the solution to the task as one involving sets, subsets and relations between them”]. The format representation was measured by the nature of the statistical information participants attributed to the format of the task on a 7-point Likert scale (1: “The information in the task has the character of frequencies”; 4: “Both equally”; 7: “The information in the task has the character of probabilities”). Finally, participants answered some socio-demographic questions.

Table 1 Bayesian problems used in the two experiments
Full size table

Unexpectedly, after completing the socio-demographic questions, we asked participants in the second part of Experiment 1 (transfer effect), to solve a different Bayesian problem (the “German measles” problem in natural frequencies, as used in Gigerenzer & Hoffrage, 1995; see Table 1) in order to measure transfer. We coded the responses numerically corresponding to the Bayesian solution (i.e., 40 out of 239 mothers) as Bayesian and the rest as non-Bayesian answers.

Participants in Experiment 2 (priming effect) first solved a set of simple mathematical problems (15 tasks, see Table 2) structurally dissimilar to the Bayesian problem (the “Admission” problem in chances), which they solved afterwards. Upon completion, participants answered questions on the operations employed using the same Likert scales as in Experiment 1; the same socio-demographic data were collected. Overall, participants were very successful in solving the set of mathematical problems (Mdn = 14, IQR = 3.5). They were statistically less successful, M–W U = 341, P < .001, r m = .55, in the priming normalization tasks (Mdn = 12, IQR = 4) compared with the priming sets tasks (Mdn = 14, IQR = 1). Despite this difference, we think that the activation of the corresponding operations was similarly strong in terms of affecting Bayesian performance. This is mainly because the majority of the participants solved most of the priming tasks in both conditions. It is reasonable to believe that corresponding arithmetic concepts were activated effectively by solving a couple of tasks only. In addition, if higher priming tasks accuracy rates lead to stronger activations then the Bayesian performance should drop down proportionally in the priming normalization condition and increase in the priming sets condition as a function of the accuracy rates; this was not the case (respectively, r pb = .022, P = .889; r pb = .092, P = .561).

Table 2 The priming of two distinct mathematical types of problems: normalization and setsa
Full size table

Results

Experiment 1 (part A): mediation of the format effect on Bayesian performance

We observed an external format gap: participants’ answers were more frequently Bayesian when the problem format involved natural frequencies than when it involved chances, χ2(1, N = 84) = 8.05, P = .005, φ = .31 (Fig. 2, middle panel). The external format manipulation—chances vs natural frequencies—affected the mental representations of the problem but not the mental representations of the format: natural frequencies led to more set representations, but not to more frequency representations, compared with chances (see Fig. 3, Experiment 1). We conducted two simple mediation analyses to test the mediation of the external format gap via the different type of mental representations. The mental problem representations mediated the effect of external formats on performance (the indirect effect was significant and the direct effect of format on performance was not), whereas the mental format representations yielded a non-significant indirect effect of external formats on performance (see Fig. 4a,b).

Fig. 2
figure 2

The effect of problem priming (Experiment 2), external formats (Experiment 1: part A), and problem transfer (Experiment 1: part B) on Bayesian performance in problems with an equal information structure, namely chances with natural sampling (left half) and frequencies with natural sampling (right half). Note that we used the “Admission” problem to measure Bayesian performance in the priming and external format effects and the “German measles” problem to measure Bayesian performance in the transfer effect experiments. Error bars represent 95 % confidence intervals

Full size image
Fig. 3
figure 3

Effect of manipulations in Experiment 1 (chances vs frequencies) and in Experiment 2 (priming normalization vs priming sets) on mental representation of problem and format (asymmetric bean plot). Bold lines Overall mean value of the scale per group, polygons density shapes determined by a normal density trace computed with a default bandwidth method using the Sheather-Jones method to select a bandwidth per batch and then averaging bandwidths over all batches (see Kampstra, 2008)

Full size image
Fig. 4
figure 4

Mediation analyses of the external format (a, b Experiment 1: part A) and transfer effects (c, d Experiment 1: part B) on Bayesian reasoning (measured as a dichotomous variable) via mental problem representations (‘Problem mental representation’; a, c) and mental format representations (‘Format mental representation’; b, d). The mediation analyses was conducted using the SPSS macro INDIRECT (Preacher & Hayes, 2008). The mediation models consist of the dichotomous variable of format or transfer effect manipulation as the independent variable, the 7-point Likert scale variable of problem or format mental representation as the mediator, and the dichotomous variable of Bayesian performance as the dependent variable. Thus, the path coefficients represent either linear or logistic regression coefficients. The reported confidence intervals represent 95 % bootstrapped confidence intervals. The numbers differ slightly due to some missing values in the mental representation questions. a path coefficient from independent variable to mediator, b path coefficient from mediator to dependent variable, ab path coefficient from independent variable to dependent variable via mediator (indirect effect), c’ path coefficient from independent variable to dependent variable (direct effect), c path coefficient from independent variable to dependent variable (total effect)

Full size image

These findings support the problem interpretation hypothesis rather than the format interpretation hypothesis because set-problem representations explained the increased performance with natural frequencies regardless of the frequency interpretation of the information. An additional test of these two hypotheses would be to scrutinize the mediation pathways via the problem and format mental representations in the performance transferred to a new problem formulated in terms of natural frequencies. Such a test follows from the argument that any natural-frequencies-training effects on Bayesian reasoning are linked to the mental problem re-structuring rather than the mental format re-structuring (e.g., Sirota et al., 2015). We tested the underlying mediation pattern of a transfer effect of working through the “Admission” problem featuring chances or natural frequencies (from the part A of Experiment 1) on a medical problem featuring natural frequencies (the “German measles” problem).

Experiment 1 (part B): mediation of the transfer effect on Bayesian performance with natural frequencies

Performance with natural frequencies or chances in a preceding “Admission” problem transferred to a great extent to the performance with natural frequencies in a medical problem. The transfer effect resulted in substantially higher performance if the preceding problem featured natural frequencies compared with chances, although the difference did not reach statistical significance, χ2(1, N = 84) = 3.57, P = .059, φ = .21 (Fig. 2, right panel). The transfer effect is less surprising, given the format gap found in the previous problem; its underlying mediation pattern, on the other hand, is surprising and informative. In general, the mediation patterns can be informative even in the situation of a non-significant total effect, because they indicate potentially interesting underlying mechanisms (e.g., Hayes, 2009). The problem—not format—representations (i.e., set-representations) employed in the preceding problem accounted for the performance discrepancy in the current problem: the significant indirect effect via problem representations accounted for substantial variance of the total effect, and the non-significant indirect effect via format representations accounted for only marginal variance of the total effect (see Fig 4c,d).

In summary, representing a problem as a set-problem, regardless of its frequency representation, accounted for the performance discrepancy in natural frequencies transferred from the previous task; such findings support the problem rather than the format interpretation hypothesis. However, the supporting evidence remains only correlational, since we did not manipulate the mediator (see Spencer, Zanna, & Fong, 2005). In Experiment 2, we planned to overcome this shortcoming and provide supportive causal evidence by manipulating the problem representations through priming either normalization-related or set-related representations.

Experiment 2: priming effect on Bayesian performance with chances

The priming affected the mental representation of the problem type, but not that of the format. Priming sets yielded significantly more set than normalization representations of the Bayesian problem, M–W U = 673, P = .038 (1-tailed exact significance test), r m = .19, but did not trigger substantially more frequency representations, M–W U = 673, P = .148 (1-tailed exact significance test), r m = .12 (see Fig. 3, Experiment 2). This effective manipulation check suggests that any effects on performance occurred likely due to the changes in the problem representation.

In line with our expectations, priming sets caused a significantly higher proportion of Bayesian answers compared with normalization priming, χ2(1) = 6.33, P = .012, φ = .27 (see Fig. 2, left panel). The effect of priming manipulation mirrored the performance of chances and natural frequencies in Experiment 1. Indeed, the performance in the set priming condition was higher than in the control chances condition although not statistically significantly so, χ2(1) = 3.08, P = .079, φ = .19, and very similar to the performance in the natural frequencies condition, χ2(1) = 1.25, P = .264, φ = .12. In contrast, performance with normalization priming resembled remarkably the performance in the control chances condition, χ2(1) = 0.60, P = .440, φ = .08, being significantly lower than the performance in the natural frequencies condition, χ2(1) = 12.81, P < .001, φ = .39. Priming set representations boosted performance, regardless of the frequency representations, further supporting the problem rather than the format interpretation hypothesis.

General discussion

The three empirical tests reported here evaluated two hypotheses proposing distinct psychological mechanisms for the facilitative effect occurring with Bayesian problems featuring partitive formats. According to the problem interpretation hypothesis, a proper problem mental representation (i.e., in terms of sets) activates appropriate knowledge, problem schemas and corresponding mathematical operations and, therefore, improves Bayesian reasoning. According to the format interpretation hypothesis, a proper format mental representation (i.e., in terms of frequencies) activates a frequency-coding mechanism and, in turn, improves Bayesian reasoning. We found here strong support for the problem interpretation hypothesis only: the set, not frequency representations, mediated the format gap (Experiment 1: part A); the set, not frequency representations, accounted for the performance with natural frequencies transferred from a preceding task (Experiment 1: part B); priming set representations, regardless of the format representations, boosted Bayesian performance with chances (Experiment 2).

The exclusive support for the problem interpretation hypothesis corroborates the nested-sets (Girotto & Gonzalez, 2001; Sloman et al., 2003) rather than the ecological rationality account (Cosmides & Tooby, 1996; Gigerenzer & Hoffrage, 1995). Indeed, if set mental representations of Bayesian problems boost performance with chances independently of their interpretation in terms of frequencies, then such interpreted representations cannot be an input for, or output of, a frequency-coding mechanism wrought by evolutionary forces as suggested by the ecological rationality account. Rather, the set representations make the nested-sets structure of the problem more visible as suggested by the nested-sets account. The robustness of the effects reported here suggests that a general rather than a specific cognitive mechanism is responsible for the interpretation and integration of the task elements (e.g., format, explicit verbal triggers) and the knowledge associated with them (e.g., schemas, problem-typical mathematical operations). Indeed, the specific role of natural frequencies in the facilitation disappears when the comparative task features an identical partitive structure accompanied with unambiguous cues leading to similar problem representations (e.g., set operations; see Sirota, Juanchich, & Hagmayer, 2014). The existence of a general cognitive mechanism is further supported by other evidence (e.g., Lesage et al., 2013; Sirota et al., 2014a; Sirota, Kostovičová, & Juanchich, 2014) and conceptual arguments (e.g., the argument of isomorphism between set-subsets relationships in natural sampling structures and some more fundamental logical operations as developed in Over, 2007).

Despite the demonstrated robustness of the problem representation effect, future research should overcome some of the methodological limitations of the experiments reported here. For example, researchers should develop more elaborated mental representation measures and assess the content of mental representations concurrently rather than retrospectively. Given the reported data patterns, however, these limitations likely played a minimal role and constrain our theoretical conclusions only marginally. Future research should also test the problem interpretation explanation for the other findings reported in the literature on Bayesian reasoning. Indeed, developing the correct problem representation may require deeper, more extensive and more active networks of pertinent numerical-problems knowledge, which would explain the positive link between numeracy and Bayesian reasoning (e.g., Chapman & Liu, 2009; Sirota & Juanchich, 2011) and the positive link between numeracy and causal problem structure facilitation (McNair & Feeney, 2015). Such a correct problem representation may also require better inhibitory control of inappropriate problem-type interpretations, which could explain the positive link between cognitive reflection ability and Bayesian reasoning (e.g., Lesage et al., 2013; Sirota & Juanchich, 2011). Finally, developing the correct problem representation may require sufficient cognitive capacity to build the adequate problem model, which could explain the effect of cognitive load on Bayesian reasoning and its link with general intelligence (e.g., Lesage et al., 2013; Sirota et al., 2014a).

Conclusion

In two experiments, we found exclusive support for the problem interpretation hypothesis, since only a problem set representation accounted for the gap between two isomorphic formats. This hypothesis offers a novel explanation of why some partitive formats encourage more normative reasoning than others and supports the nested-sets rather than the ecological rationality account of Bayesian reasoning.