Among cognitive scientists, there is currently great interest in the nature of number knowledge in general, and in the ubiquitous spatial associations of numbers in particular. The large number of investigations can be divided into two general approaches (Fischer & Shaki, 2014): On the one hand, the majority of studies so far have focused on single digit processing, such as speeded parity judgments and magnitude classification tasks. This work often relies on lateralized button responses and finds that small/large numbers are associated with left/right space, respectively (Dehaene, Bossini, & Giraux, 1993; see Wood, Willmes, Nuerk, & Fischer, 2008, for a review). Such findings are labeled as SNARC (Spatial Numerical Association of Response Codes) effects and interpreted as evidence for a spatially oriented “mental number line” with smaller numbers represented “on the left” and larger numbers successively farther “on the right” side.

On the other hand, a growing number of recent studies have focused on spatial associations in mental arithmetic. This work has documented a systematic tendency to generate or accept larger results in addition tasks and smaller results in subtraction tasks (McCrink, Dehaene, & Dehaene-Lambertz, 2007; Pinhas & Fischer, 2008; see Fischer & Shaki, 2014, for a review). Such findings are labeled as OM (Operational Momentum) effects and interpreted as evidence for attentional movements along the mental number line indicating overshoots “to the left/right” when solving subtraction/addition problems, respectively.

Together, these two lines of research converge on the conclusion that number concepts have inherent spatial associations and that these very same associations in turn affect number processing. Given this similarity of spatial biases in number processing both during single digit processing and in arithmetic contexts, it might be the case that the number-related spatial biases are the origin of arithmetical biases, in other words that SNARC is the origin of OM. This idea seems plausible because additions/subtractions lead to larger/smaller outcomes and thus activate entries further right/left on the mental number line, respectively. This hypothesis proposes a common mechanism for both single digit processing and mental arithmetic. Such a shared mechanism for spatial bias in both SNARC and OM would have considerable implications for both cognitive theorizing and educational practice. It predicts similar context sensitivity of single digit processing and mental arithmetic.

SNARC has now repeatedly been shown to depend on contextual manipulations. For example, SNARC disappears when simultaneously remembering a number sequence in descending order (Lindemann, Abolafia, Pratt, & Bekkering, 2008; see also van Dijck, Abrahamse, Acar, Ketels, & Fias, 2014) or when numbers appear in spatially incongruent positions (e.g., Fischer, Mills, & Shaki, 2010). SNARC for a given number can even be reversed by manipulating the task instructions (Bächtold, Baumüller, & Brugger, 1998; see also Ristic, Wright, & Kingstone, 2006), by presenting it within either smaller or larger numbers (Dehaene et al., 1993, Exp. 3), or by interleaving SNARC assessment with spatially incongruent responses in another task (Notebaert, Gevers, Verguts, & Fias, 2006; see also Bae, Choi, Cho, & Proctor, 2009; Pfister, Schroeder, & Kunde, 2013). Such findings indicate that SNARC relies on short-term situated number representations.

In contrast with this considerable flexibility of spatial associations in single-digit processing, the situatedness of spatial biases in mental arithmetic is not clearly established. Klein, Huber, Nuerk, and Moeller (2014) instructed participants to indicate self-calculated results of addition and subtraction problems with the mouse cursor on the corresponding locations along a visually presented number line. In one block the line was oriented from 0 on the left to 100 on the right, and in the other block the line orientation was reversed. The results showed no overt OM bias in participants’ number line estimations. However, participants’ eye movements showed a reliable OM bias that was further modulated by the congruency of the spatial–numerical mappings. This may, however, have reflected mere orientation on the reversed displays, rather than cognitive adjustments of the underlying representations. Only Knops, Zitzmann, and McCrink (2013) managed to obtain a reverse OM, but this was in 6- to 7-year-olds and with a regular spatial layout, therefore possibly reflecting underdeveloped arithmetic skills. Related to this, neglect patients produce systematic SNARC-like biases in interval bisection while having no arithmetic deficits (Zorzi, Priftis, & Umiltà, 2002). These findings converge to indicate the robustness of laboriously acquired procedural skills that operate on long-term factual knowledge during mental arithmetic (e.g., Ashcraft, 1995; McCloskey, Harley, & Sokol, 1991; see also Dehaene & Cohen, 1997).

Do these inconsistent findings from spatially flexible single digit processing and spatially robust mental arithmetic invalidate the inferred relationship between SNARC and OM? After all, OM and SNARC were substantially correlated in two recent studies (Marghetis, Núñez, & Bergen, 2014; Pinhas, Shaki, & Fischer, 2014). The lack of OM in Klein et al.’s (2014) number line estimation data might be due to their delayed manual responding: Participants had to verbalize the correct result before manually localizing it; Myachykov, Platenburg, and Fischer (2009) showed that in such tasks, OM only obtains for fast but not for slow pointing responses. Similarly, Marghetis et al. did not assess potential interactions between spatial biases for single-digit processing and mental arithmetic; they did show, however, that OM contributes to performance beyond the spatial associations evoked by the proposed outcomes. Clearly, more work is needed to (a) examine the possible flexibility of OM and (b) evaluate the relationship between single digit processing and OM.

In the present study, we tested whether reversed OM during simple arithmetic would be observed with speeded pointing to a SNARC-incongruent number line. Such a result would indicate that OM is not exclusively mediated by long-term number–space associations. OM was evaluated for both zero (e.g., 3 + 0, 3 – 0) and nonzero (e.g., 3 + 1, 3 – 1) problems. Our previous data showed that the effect is found for both types of problems, although the former produce clearer OM, probably due to reduced spatial competition during pointing, with fewer activated operands (Pinhas & Fischer, 2008).

We also evaluated the possible influence of SNARC-incongruent activity by measuring participants’ SNARCs with parity judgments before and after performing the pointing task. A regular SNARC was expected in the pretest parity judgments. Furthermore, if SNARC-incongruent arithmetic activity influences a shared spatial–numerical representation, then posttest parity performance might result in a diluted SNARC effect. Finally, a significant correlation between reversed OM and posttest SNARC could support a common origin of the SNARC and OM effects.

Method

Participants

Thirty-four students (mean age 21.7 years; 31 female, thee male, two left-handers) from the University of Dundee in Scotland participated in the experiment for course credit or payment.

Apparatus and stimuli

Stimuli appeared on an ELO 20-in. touchscreen with 1,024 × 768 pixel resolution, controlled by E-Prime software (Schneider, Eschman, & Zuccolotto, 2002).

The stimuli used for the parity judgment task were the digits 1, 2, 8, and 9. Each number was repeated 14 times per response rule (even–left or even–right), resulting in 112 randomly ordered trials total. The order of response rules was counterbalanced across participants. Numbers were presented in black on a gray background (60-point boldface Courier New font).

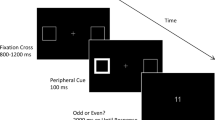
The stimuli in the calculation task consisted of 36 arithmetic problems (18 additions and 18 subtractions) derived from the digits 1–9. Twenty target problems were generated while controlling for a second-operand size of 0, 1, or 2. Problems in which the operation was predictable from the first operand magnitude (e.g., 1 + X, 9 – X) were excluded, as well as problems with results of 0, 5, and 10, since the ends and midpoint of the line are much easier to attain than other target locations. Sixteen filler problems were used to increase the variability of pointing locations. Table 1 in the Appendix presents the full list of problems. Problems were randomly presented in six successive blocks of 54 trials, resulting in 324 trials. A display sequence (Fig. 1) began with a green start box (40 × 40 pixels, 10 × 10 mm) at the bottom center of the gray screen. All of the other stimuli were black. A horizontal line (20 × 400 pixels, 5 × 100 mm) flanked by “10” on the left and “0” on the right (Courier New 30-point font) appeared at a fixed height (y-coordinate = 350 pixels, 87.5 mm above the start box), but its left edge varied randomly between left, center, and right positions. Each problem appeared inside a black framed rectangle (166 × 75 pixels, 42 × 19 mm) with a plus/minus operation sign (5 pixels wide, 20 pixels long: 1.25 × 5 mm) between the two operands.

Fig. 1
figure 1

Illustration of the experimental procedure in the calculation task (not drawn to scale)

Full size image

Procedure

Participants completed three tasks: (1) pretest parity judgments, (2) calculations, and (3) posttest parity judgments. Participants sat in front of the center of the computer touchscreen at a distance of ~50 cm. The keyboard was centered in their midsagittal plane.

In the parity judgment task, participants decided whether a presented number was odd or even. Left- and right-hand responses were recorded, respectively, via the “A” key and the “6” key on the number pad of a QWERTY keyboard. Each trial started with the presentation of a central fixation cross for 500 ms, followed by the presentation of the target number until response, followed by a blank screen presented for 250 ms. In cases of an incorrect response, a short error beep was played.

In the calculation task, participants touched the start box with their right index finger to trigger the display of an arithmetic problem, as well as the line with flankers. The first 72 trials required only single-digit (excluding 5, each digit randomly appearing nine times) localization and familiarized participants with the task demands of pointing to a reversed number line. The digit/problem disappeared after 200 ms. Participants were asked to point to the correct location of the digit/result on the line as quickly and accurately as possible. To induce fast responding, an error beep was played whenever pointing times exceeded 800 ms. We analyzed touch coordinates (in pixels, relative to the start of the number line). The calculation task ended with another 72 trials of single-digit localization, to further reinforce the inverted mapping of the single digits to space. The localization data are not further reported.

Results

The significance level was p < .01, unless specified otherwise.

Calculation task

Data were trimmed by eliminating trials with movement times (i.e., the time from the release of the start position to the next contact on the touch screen) outside 200–800 ms or with lift-off coordinates outside the start box or where the target number line was clearly missed, leaving 95.21 % of trials. Two repeated measures analyses of variance evaluated the effects of operation (addition, subtraction) and result size (4, 6 for nonzero problems, and 2, 3, 4, 6, 7, 8 for zero problems) on the horizontal landing coordinates for (1) nonzero problems (i.e., collapsed over second-operand sizes 1 and 2) and (2) zero problems (i.e., second-operand size equals 0).

The nonzero-problems analysis (Fig. 2, upper panel) revealed a main effect of result size, F(1, 33) = 393.44, MSE = 469, η p 2 = .92, confirming that the result 6 was located farther to the left than the result 4 (165 vs. 238 pixels, respectively; 18.25-mm difference). We found no main effect of operation (F < 1); however, the significant operation × result size interaction, F(1, 33) = 33.43, MSE = 226, η p 2 = .50, demonstrated a significant inverted OM for the result 6 [i.e., pointing 17 pixels/4.25 mm leftward after addition, relative to after subtraction; F(1, 33) = 13.96, MSE = 360, η p 2 = .30] but a significant normal OM for the result 4 [i.e., pointing 12 pixels/3 mm rightward after addition, relative to after subtraction; F(1, 33) = 6.4, MSE = 421, p < .05, η p 2 = .16].

Fig. 2
figure 2

Calculation task results: Mean horizontal landing coordinates (in pixels), as a function of operation and result size, for nonzero (upper panel) and zero (lower panel) problems. Vertical bars denote 95 % confidence intervals. The horizontal axis reflects the inverted number–space mapping of our experimental display (see Fig. 1)

Full size image

The zero-problems analysis (Fig. 2, lower panel) revealed a main effect of result size, F(5, 165) = 1,256.13, MSE = 442, η p 2 = .97, reflecting the inversely ordered target locations, confirmed by a significant linear component, F(1, 33) = 2,466.82, MSE = 1,115, η p 2 = .99. Importantly, a main effect of operation, F(1, 33) = 16.81, MSE = 174, η p 2 = .34, signified that participants pointed 6 pixels/1.5 mm more leftward after addition than after subtraction, demonstrating an inverted OM. We observed no significant operation × result size interaction, F(5, 165) = 1.41, MSE = 97, n.s., η p 2 = .04.

Parity judgment task

The mean reaction times (RTs) of correct responses (95.87 % of the data) were trimmed to exclude RTs shorter than 100 ms or longer than 2,000 ms, leaving 95.54 % of the data. The RT difference of right- minus left-hand responses was calculated for each digit and regressed on the digit magnitude to determine the strength and direction of the SNARC effect for each participant, separately for the pre- and posttests. The resulting set of individual regression weights was tested against zero to assess the SNARC effect.

The mean RTs for the digits 1, 2, 8, and 9 in the pretest were 560, 547, 552, and 568 ms, respectively. The mean nonstandardized regression slope was –6.68 ms/digit (range: –29.97 to 19.94 ms/digit), which differed significantly from zero, t(33) = –3.52, SD = 1.89, confirming the expected regular SNARC effect. The mean RTs for the digits 1, 2, 8, and 9 in the posttest were 527, 501, 513, and 516 ms, respectively, indicating significantly faster performance than in the pretest, t(33) = 7.47, SD = 34.21. The mean nonstandardized regression slope was –6.52 ms/digit (range: –42.80 to 13.38 ms/digit), which also differed significantly from zero, t(33) = –3.43, SD = 1.90, again indicating a significant regular SNARC effect. An additional test confirmed that the pre- and posttest SNARC slopes did not differ from one another (p = .94).

Correlational analysis

We computed individual OM scores, separately for the nonzero and zero problems, by subtracting the mean horizontal landing coordinates of subtractions from those of additions. Individual nonstandardized regression slopes were used as the SNARC scores. All correlations between the SNARC and OM measures were not significant (all ps > .05). The pre- and posttest SNARC scores were significantly related, with r = .35, p = .04.

Discussion

In the present study, we compared the spatial biases obtained in a single-digit task and in mental arithmetic. We were motivated by existing evidence for the strong context dependence of spatial biases in the SNARC effect but an apparent lack of evidence for the context sensitivity of similar biases in the OM effect. Therefore, our goal was to induce a reversed OM that would document the flexibility of this effect. A second goal was to evaluate the relationship between SNARC and OM, testing the possibility of a shared mechanism for these biases.

We obtained two main results: First, OM was reversed in the zero problems, as well as for the result 6 in the nonzero problems, with a reversed number line that required pointing to larger numbers on the left side and smaller numbers on the right side. Secondly, performance in the single-digit task did not change after as compared to before the pointing task. We will discuss these results in turn.

Consider first our finding of a reverse OM effect. Consistent with Pinhas and Fischer (2008), we found a clearer reversed OM for problems in which the second operand was zero (i.e., when there was nothing to add or subtract) than for problems with second operands of 1 and 2 (i.e., nonzero problems). The latter type of problem produced identical (i.e., inconsistent) results in both the present and our previous study, demonstrating an OM (or a reverse OM) for the result 6, but not for the result 4. In our view, these differences in the OM effect are best explained by the “spatial-competition account,” according to which OM is a result of the competing spatial biases invoked by the operands, the operation sign, and the result of an arithmetic problem (Pinhas & Fischer, 2008; Pinhas et al., 2014). With inverted spatial–numerical mappings, both operands in the nonzero problems induce spatially localized activation that is to the right of target for addition (e.g., 4 + 2), whereas for subtraction the target is either between the operands (e.g., 6 – 2) or to their right (e.g., 6 – 4). In contrast, in zero problems, both the first operand and the target activate identical spatial locations, and there is no competing second operand. This results in reduced spatial competition, and thus produces clearer OM for the zero problems than for the nonzero problems. Further support for the spatial-competition account comes from the correlated individual differences in OM and SNARC and from an operation sign spatial association effect that partially contributes to OM (Pinhas et al., 2014).

Leaving aside the observation by Knops et al. (2013; see the introduction) in children, our study was the first to show a reversed OM effect in spatial behavior. Previously, Klein et al. (2014), who also presented reversed number lines, found no evidence for OM in participants’ number line estimations with either a regular or an inverted spatial mapping. Several methodological differences between their study and ours might explain why we obtained a reliable reversal of OM. Among these are the fact that our participants were solely exposed to reversed number–space mappings and were further trained on these mappings to encourage contextual spatial adjustments. Additionally, and presumably of more importance, we pushed participants to respond rapidly. As was shown by Myachykov et al. (2009), speeded pointing is more likely to produce OM than is slow pointing.

More generally, our finding of reversed OM demonstrates that OM is related to the numbers’ current (short-term) locations and not to habitual (long-term) spatial associations. Thus, the operations of adding and subtracting are associated with their respective outcomes—larger and smaller numbers. In other words, addition and subtraction outcomes are biased toward the current spatial locations of “more” and “less,” respectively.

Consider next our findings of a normal SNARC effect in both pre- and posttest parity judgments. Importantly, SNARC was not diluted as a result of the inverted spatial–numerical mappings trained in the arithmetic pointing tasks, so there was no correlation between the spatial biases obtained for mental arithmetic and for single digits following the arithmetic task. Thus, despite establishing the context sensitivity of OM, we were unable to demonstrate with the present design a similar sensitivity for task specificity of SNARC, which had been shown in previous studies (e.g., Bächtold et al., 1998; Dehaene et al., 1993; Fischer et al., 2010; Lindemann et al., 2008; Notebaert et al., 2006; Ristic et al., 2006; van Dijck et al., 2014). Therefore, we cannot confirm the hypothesis that OM and SNARC rely on a shared mechanism.

We offer two reasons for this dissociation. One possibility relates to the fact that the parity and pointing tasks involved two different action-related reference frames. Specifically, parity decisions were made on lateralized response buttons with the index fingers, thus setting up a left–right continuum that is externally referenced. Previous work has shown that crossing the responding hands does not modulate the SNARC effect (Dehaene et al., 1993, Exp. 6), thus identifying an allocentric spatial reference frame (see also Viarouge, Hubbard, & Dehaene, 2014). In contrast, manual pointing is known to rely on egocentric spatial referencing, especially toward the end of the pointing trajectory (e.g., Fischer, Pratt, & Adam, 2007; Glover, 2004). Accordingly, SNARC was not diluted, since it involves more allocentric than egocentric spatial coding of numbers.

A second possibility relates to the working-memory-based account for spatial–numerical associations (van Dijck & Fias, 2011; see also van Dijck et al., 2014). This account postulates that number stimuli are ordinally coded in working memory according to their magnitudes or on the basis of alternatives imposed by the task instructions and/or manipulations, thereby creating temporary task-dependent spatial associations. In this view, OM was reversed due to the temporarily inverted number line representation constructed in participants’ working memory and imposed by the pointing task set. In contrast, participants were not required to construct similar inverted spatial–numerical relations during the parity judgment tasks; they could rely on their preexperimental associations, resulting in a normal posttest SNARC produced on the basis of previous experience and exposure. These two possible explanations also account for the resulting lack of correlation between SNARC and OM, but they both require further experimental investigation.

As we mentioned above, our data provide further support for the spatial-competition account of OM (Pinhas & Fischer, 2008; Pinhas et al., 2014); however, the origins of the effect are still debated. Several studies have attributed OM to shifts of spatial attention along the mental number line—the “attentional-shift account.” Support for this account has come from the influence of numbers on shifts of spatial attention (e.g., Fischer, Castel, Dodd, & Pratt, 2003); from identifying common brain parietal structures that are involved in addition and subtraction, as well as in directed saccadic eye movements (Knops, Thirion, Hubbard, Michel, & Dehaene, 2009); from observing OM in eye-fixation behavior (Klein et al., 2014); and from linking OM with attentional control measures (Knops et al., 2013). In comparison to this impressive support, the “compression account” of OM (McCrink et al., 2007; see also Chen & Verguts, 2012), which postulates that participants apply a linear transformation on the compressed mental number line representation, which in turn leads to over- or underestimating the outcome, has received less empirical support (Knops, Dehaene, Berteletti, & Zorzi, 2014; Knops et al., 2013; see also Katz & Knops, 2014).

In summary, we showed that the OM effect can be reversed through contextual cues, just as the SNARC effect can. However, this reversal was limited to certain arithmetic problems, and this relative stability of OM as compared to SNARC indicates the possibility of separate spatial-processing mechanisms for the two effects. In line with this possibility, we also discovered that the spatial biases for single digits and for arithmetic can dissociate. More research will be needed to clarify the origins of spatial biases in single-digit processing and mental arithmetic and to shed light on possible relations between these biases.