Introduction

One prominent viewpoint in judgment and decision making is based on the notion that individuals have various decision strategies at their disposal and that they will—more or less deliberately—select one or several for any given task and environment (e.g., Beach & Mitchell, 1978; Gigerenzer & Selten, 2001; Payne, Bettman, & Johnson, 1993; Weber & Johnson, 2009). More generally speaking, different underlying cognitive processes might govern observable judgments and decisions, and it is therefore vital to somehow identify these processes. To the degree that methods are capable of pinpointing how judgments and decisions are made, progress can be made in identifying determinants and bounding conditions of certain models or strategies—for example, in terms of the influence of different environmental structures (Bröder, 2003; Rieskamp & Otto, 2006), varying degrees of time pressure (Glöckner & Betsch, 2008c; Hilbig, Erdfelder, & Pohl, 2012; Payne, Bettman, & Luce, 1996; Rieskamp & Hoffrage, 2008), monetary information costs (Bröder, 2000; Newell & Shanks, 2003; Newell, Weston, & Shanks, 2003), different learning tasks and information formats (Bröder, Newell, & Platzer, 2010; Bröder & Schiffer, 2006; Pachur & Olsson, 2012; Söllner, Bröder, & Hilbig, 2013), the amount versus consistency of evidence (Glöckner & Betsch, 2012), and many more.

Despite the many extant investigations and important findings, identifying underlying decision strategies—or, more generally speaking, comparing process models of decision making—remains a challenge. Indeed “Behavioral Decision Research . . . is plagued with the problem of drawing inferences from behavioral data on cognitive strategies” (Bröder & Schiffer, 2003, p. 193). One approach is to focus on patterns of information acquisition (for an overview, see Schulte-Mecklenbeck, Kuhberger, & Ranyard, 2011) to infer which decision strategies were more or less likely to be applied (Glöckner, Fiedler, Hochman, Ayal, & Hilbig, 2012; Glöckner & Herbold, 2011; Johnson, Schulte-Mecklenbeck, & Willemsen, 2008; Payne, Bettman, & Johnson, 1988). However, information acquisition is not equivalent to information integration (Glöckner & Betsch, 2008c). For instance, a decision maker may search through all the information available but then integrate only a small subset of it. Thus, as a more common approach, the degree to which choice data are aligned with choice models or strategies is taken as an indicator of strategy use. However, the mere accordance between choices and predictions (commonly termed adherence rate) is often entirely uninformative in terms of underlying strategies (Bröder & Schiffer, 2003; Hilbig, Erdfelder, & Pohl, 2011)—mostly due to prediction overlap between competing models (Broomell, Budescu, & Por, 2011; Hilbig, 2010b) as a result of undiagnostic items (Glöckner & Betsch, 2008a; Jekel, Fiedler, & Glöckner, 2011).

An elegant solution to this “strategy classification problem” was proposed by Bröder and Schiffer (2003). Their outcome-based strategy classification method compares models (representing decision strategies) in terms of how well they account for choice vectors across a set of diagnostic item types that allow for discriminating between competing models. However, a limitation of the method is that it only allows for the inclusion of models with deterministic choice predictions. In the present work, we show how to overcome this limitation so as to include probabilistic predictions that are often made by psychologically plausible process models of decision making. To this end, we will explain Bröder and Schiffer’s (2003) approach in some detail below, demonstrate the currently existing limitations, and propose a generalization that remedies the latter. In all of the following, we will deliberately maintain a practical—rather than a technical—focus in the hope that it will be instructive for researchers aiming to apply the method proposed.

Outcome-based strategy classification

The outcome-based strategy classification method proposed by Bröder and Schiffer (2003) rests on the general idea of comparing all models (in their case, decision strategies for multicue inferences) in terms of how well each accounts for choice data, while allowing only for random strategy execution errors and penalizing model flexibility (cf. Bröder, 2010). The strategy with the largest a posteriori likelihood, as compared with all other models, is then inferred to be the one that (most likely) produced the observed choices. This approach has recently been extended to multiple dependent measures beyond choices (Glöckner, 2009; Jekel, Nicklisch, & Glöckner, 2010) and the possibility of strategy mixtures (Davis-Stober & Brown, 2011), thus solving the problem of complete choice prediction overlap between models and the questionable assumption of perfect strategy consistency, respectively.

The method proposed by Bröder and Schiffer (2003) is best understood in the context of an example. For this purpose, Table 1 depicts a set of materials for a multicue inferences task: Participants infer which of two choice options (e.g., cities), A or B, scores higher on some criterion (e.g., population). They are provided with (or learn) the value of four cues that are probabilistically related to the criterion (e.g., whether or not a city has an international airport, is a state capital, has a university, and/or a major league football team). In the simplest task version, cues are present (1) or absent (0), and the degree to which each predicts the criterion (i.e., the predictive validity; e.g., Gigerenzer & Goldstein, 1996) is known to the decision maker or learned through feedback. For our example, assume that cue validitiesFootnote 1 are .90, .80, .70, and .60 for cues 1–4, respectively.

Table 1 Cue patterns for three item types and choice predictions of strategies taken from Bröder and Schiffer (2003)
Full size table

In the example depicted in Table 1, there are three item types that are defined by different cue patterns; importantly, the decision strategies under consideration make different choice predictions across these item types. A weighted additive strategy (WADD; choose the option with the higher sum of cue values weighted by their validities) would predict choice of options A, B, and A, respectively. By comparison, an equal weights strategy (EQW; choose the option with the higher sum of cue values, ignoring cue validities) would predict A, B, and guessing. A lexicographic take-the-best strategy (TTB; consider cues in order of their validity; choose according to first discriminating cue) would predict choice of option A across all three item types. Finally, a guessing strategy (GUESS) would choose options A or B with 50 % probability in each of the three item types. As such, each strategy yields a distinct choice vector, as shown in Table 1.

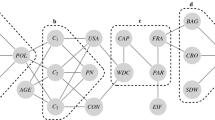
Choice items from each item type are presented repeatedly (say, 100 times each), such that the observable choice data for each individual consist of the frequency of A- vs. B-choices per item type. This situation can be understood in terms of a simple multinomial processing tree modelFootnote 2 (Batchelder & Riefer, 1999; Erdfelder et al., 2009) such as the one depicted in Fig. 1: In each of the three item types, an individual will choose in line with a model’s prediction (with probability 1 − e) or commit a strategy execution error (probability e), thus choosing the option not predicted by the strategy. Whenever a strategy predicts guessing (e.g., EQW in item type 3), the error probability in the corresponding item type for this strategy is fixed at .50. For example, WADD would be represented by the model equations

Fig. 1
figure 1

Multinomial processing tree representation of the task structure in Table 1

Full size image
$$ \begin{array}{l}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 1\right)=\left(1-{e}_1\right)\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 1\right)={e}_1\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 2\right)={e}_2\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 2\right)=\left(1-{e}_2\right)\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 3\right)=\left(1-{e}_3\right)\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 3\right)={e}_3\hfill \end{array} $$

However, little is gained by estimating these models without any further restrictions on the parameters, since the unconstrained error probabilities merely represent (item-specific) adherence rates. Moreover, the models are saturated and, therefore, do not allow for performing tests of goodness of fit. To overcome these problems, the strategy classification method draws on the key assumption that strategy execution errors—that is, choices not in line with a model’s predictions—are constant across the item types, such that e 1 = e 2 = e 3. By adding this restriction, the model becomes overidentified and, thus, testable.

For example, TTB predicts choice of option A in all three item types (see Table 1). Thus, the probability of choosing option A—which cannot be expected to be equal to one, since decision makers will make occasional random errors—should be constant across all three item types. A strategy is therefore only “allowed” random errors, whereas systematic errors (i.e., different probabilities of choosing in line with the model’s predictions across item types) lead to model misfit. The idea of allowing for random errors while penalizing systematic error (which contradicts a model or strategy) is the core advantage of this approach, as compared with simply counting the number of strategy-consistent choices (which suffers from inherently ignoring systematic error, cf. Bröder & Schiffer, 2003; Hilbig, 2010a). So, in the present example, the fit of TTB is determined after constraining e 1 = e 2 = e 3, where e denotes the probability of choosing option B in each of the three item types in Table 1, respectively.

In multinomial modeling, parameter estimates are sought that minimize the distance between observed and predicted choice proportions. Say each item type is presented 100 times, and let an individual’s frequency of choosing option A be 80, 70, and 60 across items types 1–3, respectively. Then, for TTB, e 1 = e 2 = e 3 = .30 will minimize the difference between observed and predicted choices (the predicted frequency of choosing option A is 70 out of 100 in each item type). The most common (to-be-minimized) distance measure used in multinomial modeling is the log-likelihood ratio statistic G 2 which is asymptotically χ 2-distributed under H0 (i.e., the model holds). Minimization proceeds by means of the EM algorithm (Hu & Batchelder, 1994), as implemented, for example, in the multiTree freeware tool (Moshagen, 2010).

To actually use this approach for the purpose of strategy classification, each model under consideration is consecutively fitted to the data, so that the fit of each model or strategy is assessed separately per individual data set. To compare models or strategies in terms of fit while penalizing flexibility, Bröder and Schiffer (2003) and Glöckner (2009) relied on the Bayesian information criterion (BIC; e.g., Wasserman, 2000), which can be computed from G 2, the total number of choices, and the model’s degrees of freedom. The degrees of freedom are the number of free parameters subtracted from the number of free category frequencies. In the present example, both WADD and TTB have one free parameter (because the three error parameters are constrained to be equal), and thus df = 2 (since there are three free category frequencies—one for each item type). EQW also has one free parameter (because e 1 and e 2 are constrained to be equal and e 3 is fixed at .50), and thus df = 2. GUESS has no free parameters (all error parameters are fixed at .50), and thus df = 3. Note that freeware such as multiTree automatically computes both G 2 and information criteria such as BIC, along with the error parameter estimates and their standard errors.

For strategy classification, the model with the smallest BIC is regarded as the data-generating strategy (i.e., the one “used” by the decision maker). In addition, an upper bound of .30 or .40 for e (excluding item types where e is fixed at .50 to represent guessing) is usually implemented; that is, only models are considered to which decisions conform at least somewhat better than chance (Bröder & Schiffer, 2003; Glöckner, 2009)—although it remains a matter of idiosyncrasies how much better than chance a model is required to perform. In addition, it is necessary to test the absolute fit of each model (as outlined above, G 2 is χ 2-distributed under H0), retaining only models that fit the data for classification, thus ensuring that phantom data sets (i.e., data sets generated by a model outside the consideration set) are not falsely classified (Moshagen & Hilbig, 2011). Otherwise, classification results may be severely biased in unknown ways.

Limitations

As was described above, the outcome-based strategy classification method proposed by Bröder and colleagues can be applied to any set of strategies, so long as item types can be found across which models make qualitatively distinct predictions (Jekel et al., 2011).Footnote 3 However, as it is, the method also imposes certain limitations in terms of the models that can be considered and, thus, compared. Specifically, models cannot be implemented with probabilistic choice rules (thus, predicting different choice probabilities across item types), because error probabilities are necessarily constrained to equality across item types (or fixed at .50). In Bröder and Schiffer’s (2003) approach, error probabilities are conceptualized to reflect mere execution errors (resulting from slips of the finger, fatigue, etc.) that should be independent of item type. Whenever no such execution error occurs, the probability that choices are in line with a model’s predictions—if the model holds—is assumed to be equal to one, thereby implying a deterministic association. However, if the data-generating process predicts varying choice probabilities across item types, the approach cannot distinguish whether observed choices vary (1) due to varying execution errors or (2) due to different predicted choice probabilities per se. As a result, model misfit will occur, in turn leading to misclassifications or nonclassifications—even if the process is actually compatible with one of the strategies under consideration.

For example, WADD is implemented such that it predicts choice of option A in item type 1, B in item type 2, and A in item type 3—all with the same probability. In other words, this implementation of WADD requires that choosing option A in item type 1 is just as likely as choosing B in item type 2, and so forth. Whereas a WADD strategy that is meant to reflect strictly deliberate serial calculation of the difference between choice options in weighted sums (of cues) would potentially make this prediction, practically all psychologically plausible process implementations of WADD are incompatible with this requirement. For example, both evidence-accumulation models (Busemeyer & Townsend, 1993; Ratcliff & McKoon, 2008; Ratcliff & Smith, 2004; Roe, Busemeyer, & Townsend, 2001) and connectionist models (e.g., Glöckner & Betsch, 2008b; Glöckner & Herbold, 2011)—both of which, roughly speaking, approximate WADD—inherently predict that choice probability is a function of the difference in evidence between options (cf. Luce’s choice rule; e.g., Luce, 1977). The more strongly weighted sums speak for one option relative to the other, the higher choice probability should be. By implication, error probabilities cannot be equal across item types.

Indeed, the notion that choice probability is a function of the difference between choice options has a long tradition. Mosteller and Nogee (1951) showed for monetary gambles that choice probability was an increasing S-shaped function of the amount to win (resembling psychometric functions typically found in psychophysics). Correspondingly, Dashiell (1937) reported that mean choice times decreased with increasing preference strength (see also Petrusic & Jamieson, 1978). Overall, it is well-established that choice probability, choice consistency, and response time typically depend on the difference between choice options (Birnbaum & Jou, 1990). This is also in line with linear order research (Moyer & Bayer, 1976; Parkman, 1971), which has long shown that the larger the symbolic “distance” between two choice options, the shorter response times, the fewer errors, and the more choice consistency (for recent extensions to multicue inferences, see Brown & Tan, 2011; Pohl & Hilbig, 2012). The same pattern also held in the data reported by Platzer and Bröder (2012) and, thus, a setup closely resembling the one exemplified in Table 1: In a reanalyses of their data,Footnote 4 we found that the choice probability (albeit aggregated over participants) across the 45 trials was a function of the difference in weighted sums of cue values per trial with R 2 = .55.

As a consequence of constraining error probabilities to be equal across item types in Bröder and Schiffer’s (2003) approach, the relationship between the difference in evidence and choice probability is artificially reduced to a step function centered at .50. Specifically, the deterministic variant of WADD is merely a special case of the probabilistic version: Both the deterministic implementation of WADD and any probabilistic variant would predict that choice between options with exactly the same weighted sums would be a guess—that is, to fix the error at .50. However, the deterministic WADD further implies that the choice probability is 0 or 1 as soon as there is even a miniscule difference in evidence between the options. By contrast, models with probabilistic choice rules imply an increase of choice probability with increasing evidence-difference, which may, in the extreme, be a step function (as assumed by the deterministic WADD) but could also and will more commonly show a gradual increase.

Importantly, a process producing such a gradual increase in choice probability with growing evidence-difference will produce misfit in the above classification method because choice probabilities (and thus errors) will vary across item types. Put another way, the requirement of constraining error parameters to equality in the classification method rules out consideration of process models, such as evidence-accumulation models, that may be considered psychologically plausible implementations of WADD. Of course, this problem is not limited to the WADD strategy: For example, one may also think of a probabilistic TTB-version, assuming that choice probability is a decreasing function of the number of cues that must be considered before a discriminating one is found. The more steps TTB requires before a choice can be made, the larger the probability of a strategy execution error.

To demonstrate this limitation, we ran a recovery simulation similar to the one reported by Bröder and Schiffer (2003; see also Glöckner, 2009; Moshagen & Hilbig, 2011): We generated 1,000 data sets, each with 30 simulated choices for each of the three item types in Table 1. However, unlike in the original simulation by Bröder and Schiffer, 2003), in which the deterministic form of WADD was used to generate data (showing close to perfect recovery rates of 99 % in the case of 10 % random strategy execution errors; see also Moshagen & Hilbig, 2011), the data-generating strategy was a probabilistic WADD strategy (henceforth, WADDprob) described by the function

$$ p(A)=\frac{1}{1+{e}^{\left(-4\times \delta \right)}}, $$

where p(A) is the probability of choosing option A and δ is the difference between option A and option B in the sum of cue values weighted by their validities. This strategy predicts choice of option A with probabilities .88, .40, and .77 across the three item types in Table 1.Footnote 5 Correspondingly, the average probabilities of strategy execution errors (for choosing A, B, and A, respectively) in the simulated data sets were e 1 = .12, e 2 = .40, and e 3 = .33 for the three item types, respectively. Next, we applied the standard classification method as described above to these data sets, thus determining the error parameter estimates, model fit, and BIC for WADD, EQW, TTB, and GUESS (for model equations and an exemplary model file for use in the multiTree freeware, see the Appendix). Results were clear-cut: Less than 30 % of simulated data sets were indeed classified as WADD, whereas most (67 %) were left unclassified due to absolute model misfit (with a type I error of .05) or an average error larger than .30. The remaining 3.5 % were misclassified as EQW or TTB. Clearly, it seems unsatisfactory to classify so few data sets as WADD when it actually is the underlying (data-generating) strategy, albeit in the form of a psychologically more plausible implementation that corresponds to a naïve evidence-accumulation model.

Generalized outcome-based strategy classification

The limitation as explained and demonstrated above calls for a simple extension of Bröder and Schiffer’s (2003) approach. Ideally, it should be possible to include models that predict varying error probabilities across item types—although with a specific rank order of error probabilities. Indeed, the WADDprob model specified above could easily be implemented simply by fixing e 1 = .12, e 2 = .40, and e 3 = .33 in the original WADD model (rather than e 1 = e 2 = e 3). However, doing this implies the strong assumption of a strictly linear one-to-one relationship between the weighted sums of cue values and choice probability and, thereby, would lead to misfit of a data pattern yielding, say, e 1 = .02, e 2 = .31, and e 3 = .08, even though this pattern is produced by a highly similar WADDprob model specified as

$$ p(A)=\frac{1}{1+{e}^{\left(-10\times \delta \right)}}. $$

Since the assumption of a one-to-one relationship is overly restrictive, a more viable approach is to assume a monotonically increasing mapping function between evidence-difference and choice probability. Such a sufficiently general form of WADDprob can be obtained by applying order constraints on the error probabilities. Thus, an appropriate approach is to apply the constraints e 1 ≤ e 3 ≤ e 2, rather than constraining all error parameters to be equal (as in the deterministic WADD) or to fixed values (representing only one particular specification of WADDprob). Note that the difference in weighted sums of cue values is .50 (for option A) in item type 1, .10 (for option B) in item type 2, and .30 (for option A) in item type 3 (see Table 1). So, any WADD model with a probabilistic choice rule (and thus, choice probability increasing monotonically with the difference in weighted sums) must predict that model-consistent choices are most likely in item type 1 and least likely in item type 2, and thus e 1 ≤ e 3 ≤ e 2.

Fortunately, the constraint e 1 ≤ e 3 ≤ e 2 can easily be implemented in the multinomial processing tree framework by means of parametric order constraints (Knapp & Batchelder, 2004). In the present example, the constraint e 3 ≤ e 2 can be implemented by replacing e 3 by e 3 = p 2 × e 2, which essentially forces e 3 to be smaller than or equal to e 2 (any parameter in a multinomial model represents a probability, so p 2 cannot exceed 1). Likewise, the constraint e 1 ≤ e 3 is introduced by replacing e 1 by e 1 = p 1 × e 3 = p 1 × p 2 × e 2. The complete general WADDprob model with e 1 ≤ e 3 ≤ e 2 is thus represented by the model equations

$$ \begin{array}{l}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 1\right)=\left(1-{e}_2\right)+{e}_2\times \left(1-{p}_2\right)+{e}_2\times {p}_2\times \left(1-{p}_1\right)\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 1\right)={e}_2\times {p}_2\times {p}_1\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 2\right)={e}_2\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 2\right)=\left(1-{e}_2\right)\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 3\right)=\left(1-{e}_2\right)+{e}_2\times \left(1-{p}_2\right)\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 3\right)={e}_2\times {p}_2,\hfill \end{array} $$

wherein e 3 from the original model equations has been replaced by p 2 × e 2 and e 1 replaced by p 1 × p 2 × e 2. Say each item type is presented 100 times, and let the frequency of choosing option A be 80, 40, and 70 across items types 1–3, respectively. Then, the parameter estimates of the above model are e 2 = .40, p 1 = .667, and p 2 = .75. Consequently, e 3 = p 2 × e 2 = .75 × .40 = .30 and e 1 = p 1 × e 3 = .667 × .30 = .20, thus matching exactly the to-be-expected error parameter estimates given the data. Although this reparameterization does not change the dimensionality of the parameter space (since the two unknown parameters e 1 and e 3 are replaced by the two unknowns p 1 and p 2), the admissible parameter space is reduced to those patterns compatible with the order restrictions on the parameters. In other words, a data pattern incompatible with the order constraint (e.g., one implying e 3 = .40 and e 2 = .30) would produce misfit. A peculiarity in this context is that the WADDprob is a saturated model (with zero df), yet unable to fit arbitrary data patterns. This is because the parameters are bounded by [0…1], so that misfit will occur whenever the data would imply parameter estimates outside the admissible interval. For example, if e 3 is actually greater than e 2, the reparameterization e 3 = p 2 × e 2 could be satisfied only by p 2 > 1. We return to the issue of how to assess the fit of the WADDprob below.

By the same logic, parametric order constraints allow for implementing an upper bound for strategy execution errors. As was outlined above, it is common—and, as shown by Bröder and Schiffer (2003), indeed necessary—to set such an upper bound, since any model should predict choices better than chance level. Whereas in the original method (and extensions such as Glöckner’s, 2009) models were excluded post hoc if the average error estimate exceeded a certain threshold, a more elegant solution is available within the present extension. We can require that all error probabilities are smaller than or equal to some constant representing chance level (.50 in the case of binary choices). This, too, is a simple parametric order constraint in the multinomial framework and can thus be implemented in the same way. Specifically, in the example of the WADDprob model above, we can implement e 1 ≤ e 3 ≤ e 2 ≤ .50 by replacing e 2 by e 2 = c × e 2′, where c is a constant fixed at .50. The corresponding model equations are

$$ \begin{array}{l}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 1\right)=\left(1-c\right)+c\times \left(1-{e}_2^{\prime}\right)+c\times {e}_2^{\prime}\times \left(1-{p}_2\right)+c\times {e}_2^{\prime}\times {p}_2\times \left(1-{p}_1\right)\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 1\right)=c\times {e}_2^{\prime}\times {p}_2\times {p}_1\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 2\right)=c\times {e}_2^{\prime}\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 2\right)=c\times \left(1-{e}_2^{\prime}\right)+\left(1-c\right)\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 3\right)=\left(1-c\right)+c\times \left(1-{e}_2^{\prime}\right)+c\times {e}_2^{\prime}\times \left(1-{p}_2\right)\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 3\right)=c\times {e}_2^{\prime}\times {p}_2.\hfill \end{array} $$

Fixing c = .50 thus ensures that e 2 cannot exceed .50; or, in turn, if choice data imply e 2 > .50, this will induce misfit. Of course, the constraint that all error parameters (except those fixed at .50 to predict guessing) should be smaller than a constant representing chance level should be implemented for all to-be-compared models. Then, as another key advantage, one does not need to exclude models post hoc on the basis of some upper bound for the average error (set somewhat arbitrarily). Instead, all models are required to account for choices at least as good as chance.

Model selection criterion

As was described above, the original method proposed by Bröder and Schiffer (2003) and Glöckner’s (2009) extension rely on information criteria such as BIC for strategy classification: For each model (strategy) and data set, the fit is determined while penalizing model flexibility in terms of free parameters. Penalizing for flexibility is a desirable attribute, since a highly flexible model adjusts not only to systematic patterns, but also to random noise in the data. However, BIC only roughly corrects for model flexibility by taking into account the number of free parameters, while ignoring functional complexity—that is, how much of the data space a model can account for (Myung, Navarro, & Pitt, 2006). As such, information criteria (AIC and BIC) cannot fully measure the parametric complexity of the stochastic specifications considered herein. In simple terms, this is problematic, since models with the same number of free parameters can differ greatly in complexity. For example, WADDprob (with e 1 ≤ e 3 ≤ e 2 ≤ c = .50) has three unknown parameters—exactly like a model with completely unconstrained error parameters (letting e 1, e 2, and e 3 freely vary). However, WADDprob can actually account for (i.e., fit) a substantially smaller portion of the data space than can a model with completely unconstrained error parameters and is, therefore, far less flexible. When comparing two models that differ in the functional form but comprise the same number of free parameters, information criteria always select the model with the largest likelihood. Classifications based on information criteria would thus induce a systematic bias.

A viable solution is to rely on selection criteria that take the functional form of a model into account (Pitt, Myung, & Zhang, 2002). This is the case for model selection criteria based on the principle of minimum description length (MDL; Grünwald, 2007; Myung, 2000; Myung et al., 2006), which have already been used in decision strategy classification (Davis-Stober & Brown, 2011). In simple terms, this approach can be understood as an implementation of Occam’s razor (Myung & Pitt, 1997) with the idea of penalizing flexibility in the sense of how much of the data space a model could potentially account for. Once parametric order constraints are added to models, this approach to penalizing flexibility—unlike those correcting only for the number of free parameters (AIC and BIC)—will ensure that the model comparison remains “fair.” Of course, model selection drawing on the MDL principle will (typically) more heavily panelize models involving many free parameters than models with only a few free parameters. Thus, using the MDL principle ensures that the increased flexibility of the WADDprob (as compared with the deterministic WADD or TTB) is still appropriately taken into account in the comparison process.

The MDL of a model is the sum of goodness of fit and a model complexity term, which, in the case of multinomial models, can be defined as the sum of the maximum likelihoods of all possible data vectors from the outcome space. Models that are able to account for almost arbitrary data patterns will therefore receive a larger complexity term, relative to models that fit only a few data patterns. Since it is difficult for many applications to find an explicit solution, the Fisher information approximation (FIA) of the complexity term (cFIA; Rissanen, 1996; Wu, Myung, & Batchelder, 2010), in conjunction with numerical integration techniques, is often used for approximation. Note, however, that cFIA can be misleading in small samples—in the extreme, leading to the selection of the more complex model with certainty (Navarro, 2004; Wu et al., 2010). As a practical remedy, Heck, Moshagen, and Erdfelder (2014) proposed estimating the lower bound sample size, ensuring stable rank orders of FIA complexity terms. Model comparisons using FIA should be performed only if the actual sample size exceeds this lower bound sample size.

Recovery simulations

To test whether the generalized strategy classification method with the MDL selection criterion will reliably identify underlying strategies, including those with probabilistic choice rules, we ran a recovery simulation similar to the one reported above: We generated 1,000 data sets for each of the strategies—viz. WADDprob as specified above (predicting choice of option A with probabilities .88, .40, and .77, respectively), EQW, and TTB (each with a strategy execution error of .10), and GUESS. For each of the three item types, 30 trials were simulated per data set.

For each data set, we then determined the fit and MDL of each of the models under consideration using multiTree (Moshagen, 2010). As was explained above, WADDprob was represented by a multinomial model constraining e 1 ≤ e 3 ≤ e 2 ≤ c = .50. The constraints for EQW were e 1 = e 2 ≤ e 3 = c = .50, and those for TTB e 1 = e 2 = e 3 ≤ c = .50. Finally, GUESS was represented by e 1 = e 2 = e 3 = .50. Across all data sets and strategies, the simulation revealed a recovery rate (proportion of correct classifications given data-generating models) of 97.4 %, which is highly satisfactory given the moderate number of simulated trials per item type. The recovery rates per strategy were 99.2 % for WADDprob, 99.7 % for TTB, 97.4 % for EQW, and 93.2 % for GUESS, also indicating that there was no particular bias for any of the models (Cohen’s w = .06).

Despite these promising results, an important caveat needs to be addressed. As was previously argued with respect to Bröder and Schiffer’s (2003) and Glöckner’s (2009) approaches, the classification rests entirely on the assumption that the data-generating model is among those considered. Data generated by a nonconsidered model will lead to misclassifications and, thus, heavily flawed conclusions (Moshagen & Hilbig, 2011). In the original approach by Bröder and Schiffer (2003), this could be circumvented by assessing the absolute fit of each model to each data set (by means of G 2) prior to entering the model comparison competition, thus retaining only models for classification that fit the data. As was shown by Moshagen and Hilbig (2011), data generated by a model outside the set of those considered will then induce misfit and remain unclassified (as is desirable).

However, in the present generalization, assessment of absolute model fit is no longer feasible using usual procedures, because some models in the comparison, such as WADDprob, differ from the saturated model in inequality constraints only. In the presence of such inequality constraints, the limiting distribution of G 2 is no longer χ 2(df), but a weighted mixture of independent χ 2 distributions (see, e.g., Davis-Stober, 2009). Although a number of methods for conducting formal hypothesis tests in corresponding situations exist (Andrews, 2000; Chechile, 1998; Davis-Stober, 2009; Klugkist & Hoijtink, 2007), none of these is particularly straightforward or implemented in standard software. An alternative approach equally suited in the present context is to additionally implement a baseline model in the classification. Footnote 6 Specifically, a model with entirely unconstrained error parameters (letting e 1, e 2, and e 3 vary freely) should be added to the set of competing models. This baseline model is maximally flexible, since it can account for any choice vector without misfit. Thus, it will also be penalized most strongly for its flexibility by the MDL criterion. Nonetheless, a phantom data set produced by some unknown alternative strategy—and thus, one at least somewhat distinct from those produced by the models considered—should be best accounted for by this baseline model.

To test this solution, we reran the above recovery simulation adding another data-generating strategy (a “phantom” strategy) that predicts guessing in item type 1 and choice of option B in item types 2 and 3, respectively. For example, this vector would be produced by an equal weights strategy that ignores the first cue. Classifying the 1,000 phantom data sets with the models above, but without a baseline model, revealed that 93 % of the data sets were falsely classified as EQW, and the remaining 7 % were falsely classified as GUESS. By contrast, including the baseline model in the model competition resulted in 99.9 % of the phantom data sets remaining unclassified (since the baseline model accounted for these data sets best). At the same time, inclusion of the baseline model did not negatively affect the recovery rate of the other data sets (i.e., those generated by models actually included in the competition), which was 96.8 %. In other words, inclusion of a baseline model (letting e 1, e 2, and e 3 vary freely) ensured that phantom data—generated by some unknown strategy outside the set of models considered—remained unclassified, whereas data sets generated by a model actually under consideration continued to be (correctly) classified.

In sum, we have shown that the proposed generalization with parametric order constraints allows for the inclusion of models with probabilistic choice rules and that strategy classification based on this method is reliable. However, as holds for previous variants of the strategy classification method, the reliability of the results also depends on the number of trials per item type. In particular, the lower bound sample size (Heck et al., 2014) ensuring the correct rank order of TTB and WADDprob complexity terms (cFIA) in the setup used above was n′ = 27 per item type. Since the number of trials required to ensure stability in the rank orders depend on both the models under consideration and the number of item types, we recommend routinely determining the lower bound sample size prior to collecting data.

Moreover, if one wanted to distinguish between the same model with a deterministic versus probabilistic choice rule (e.g., the original deterministic WADD and our WADDprob), more trials per item type would be advisable. In corresponding simulations (generating data under both model variants and entering both models into the classification competition), we found that with 30 trials per item type, as used above, the recovery rate was satisfactory at 85 %. Nonetheless, increasing the number of trials per item type to 50 yielded a still more satisfactory recovery rate of 92 %, and an additional increase to 100 trials per item type resulted in an excellent recovery rate of 96 %. As these findings demonstrate, the required number of trials heavily depends on the models to be distinguished, although a lower bound of 27 trials per item type seems necessary for obtaining stable estimates of the MDL selection criterion.

Experiment

To demonstrate the usefulness of the present generalization, we additionally ran an experiment. The setup closely matched the situation depicted in Table 1 with three item types for which the classical models (WADD, TTB, EQW, and GUESS) made the exact choice predictions displayed in Table 1. Likewise, WADDprob again predicted e 1 ≤ e 3 ≤ e 2. The specific cue patterns used can be found in the supplementary material, along with the raw choice data of participants. The task for participants was modeled on typical previous investigations: Participants were instructed to repeatedly choose one of two options, labeled “A” and “B.” They were told that these represent fictitious products and that they should infer which product is superior in terms of quality. For each inference, they were openly provided with the values of four cues, explained to them as fictitious expert ratings. It was further explained that the four experts differ in how well they typically predict product quality (i.e., cue validity—namely, .90, .80, .70, and .60, respectively). To ensure that automatic information integration would not be hampered by enforcing serial search (Glöckner & Betsch, 2008c; Hilbig & Glöckner, 2011), all information was openly available in a matrix. Columns represented the choice options (the order of options was counterbalanced across trials), and rows contained the cue values (with “+” and “−” representing a positive vs. negative cue value, respectively). The order of rows was constant, with cues in descending order of validity.

Participants made 32 choices per item type and, thus, 96 in total. They were promised feedback about the quality of their inferences at the end of the task, and the normative Bayesian solution (Lee & Cummins, 2004) served as the benchmark against which participants’ responses were compared. Participants’ decisions conformed to this normative solution very well (M = 90 %, SE = 1 %), and the task including all instructions required 8.5 min on average. We recruited a total of 79 participants (44 female; 18–27 years of age, M = 20 years, SD = 2.2 years). They completed the current task as part of a 45-min experimental battery of otherwise unrelated tasks.

Strategy classification proceeded exactly as described in detail above. First, we took the classical approach: For each individual data set and model (WADD, EQW, TTB, and GUESS), we computed the error parameter estimates, excluded strategies displaying significant model misfit or an average error probability exceeding .40, and, of the remaining strategies, selected the one with the smallest BIC. As can be seen in Table 2, more than one third of data sets were left unclassified due to absolute model misfit (with a type I error of .05) or an average error larger than .40 for all models considered. The majority of classified data sets were best accounted for by WADD. By comparison, using the generalized approach as proposed above, only three data sets (3.8 %) were left unclassified—that is, the baseline model accounted for these data sets best—whereas the clear majority was best explained by WADDprob. Closer inspection revealed that out of these data sets best accounted for by WADDprob, 41 % were originally classified as WADD, and the remaining 59 % were originally left unclassified due to model misfit.

Table 2 Classification results based on the classical approach (classifying data sets by means of the BIC, excluding models producing significant misfit or an average error above .40) and our generalized approach (classifying data sets by means of the MDL)
Full size table

Overall, the findings demonstrate two noteworthy aspects. First, from a modeling perspective, the generalized approach proposed herein will remedy the drawback that a substantial proportion of data sets may have to remain unclassified, even though they can actually be accounted for. Decision strategies approximating weighted–additive information integration with a probabilistic choice rule will lead to misfit in the classical approach, because they inherently violate the requirement of a constant choice probability across item types. However, once a probabilistic model can be included in the comparison by means of the generalized approach proposed herein, practically all data sets can be accounted for.

Second, from a substantive point of view, our findings corroborate recent investigations concluding that there is a strong predominance of cognitive processes characterized by weighted-additive information integration (Glöckner & Betsch, 2008c, 2012; Glöckner, Betsch, & Schindler, 2010; Glöckner & Bröder, 2011; Glöckner & Hodges, 2011) in an open display format in which information search costs are minimized. Indeed, 87 % of data sets were best accounted for by WADD or WADDprob. However, for the most part, choices are unlikely to stem from sequential deliberate calculation of weighted sums (as must be presumed in the classical model comparison approach and represented by the classical WADD). Rather, they mostly conform to plausible cognitive process models assuming automatic/intuitive information integration, as represented by the probabilistic version of WADD, which predicts that choice probability is a function of the difference in evidence between options.

Discussion

Much research in judgment and decision making has focused on which decision strategies are used by whom and under which circumstances—that is, which process models account for observable behavior. However, investigations of this nature have been fraught by the challenge to infer underlying strategies or processes from choice data. One elegant and commonly applied solution was proposed by Bröder and Schiffer (2003), who made use of different item types across which to-be-compared strategies/models make qualitatively distinct predictions. Thus, choice vectors were diagnostic for the models under consideration, which were implemented with deterministic choice rules, allowing for a constant strategy execution error across item types (Bröder, 2010). Other extensions of this method to multiple dependent measures (Glöckner, 2009; Jekel et al., 2010) or strategy mixtures (Davis-Stober & Brown, 2011) notwithstanding, we herein addressed a limitation of this approach: Models with probabilistic choice rules—predicting a specific rank order rather than constant or exact choice probabilities across item types—could not be included in the comparison. The upshot of this limitation has been that psychologically plausible implementations of integration models—such as a weighted additive strategy for multicue inferences—were not taken into account or forced to produce misfit due to their inherently probabilistic choice predictions. Among these plausible models are evidence accumulation and neural network models (for an overview, see Glöckner & Witteman, 2010).

Herein, we have proposed a remedy for this limitation, using the technique of implementing parametric order constraints (Knapp & Batchelder, 2004) in multinomial processing tree models (Batchelder & Riefer, 1999; Erdfelder et al., 2009) and relying on minimum description length as the model selection criterion (Wu et al., 2010), in combination with a baseline model to rule out misclassification of phantom strategies. By means of this generalization, models can be included that predict a specific rank order of model-consistent choice probabilities across item types. As shown in a series of simulations, this extension of Bröder and Schiffer’s (2003) approach reliably uncovers underlying strategies. Also, by adding a maximally flexible baseline model into the competition, the caveat of false classifications of data sets produced by models not under consideration can be counteracted. An empirical demonstration further revealed that the generalized approach put forward herein indeed practically eliminates nonclassification due to model misfit and provides evidence for cognitive processes in line with psychologically plausible probabilistic integration models.

Note that the extension proposed herein actually allows for comparing various types of models within the same competition. For one, the typical deterministic models (predicting the same strategy execution error across item types) can be considered. In addition, models predicting an order of choice probabilities (such as a weighted additive model with a probabilistic choice rule) can be included. Note that, as in the original method, it is also possible to consider a model that predicts exact choice probabilities for each item type; thereby, even different specifications of the same model class could be distinguished (e.g., two specific evidence-accumulation models). In any case, models need not yield the same degree of specification, and varyingly strict model variants may be put to the test. Of course, these possibilities are not limited to the realm of probabilistic inferences. For example, Bröder and Schiffer’s (2003) original method and the present generalization could just as well be applied to risky choice tasks where item types would be defined as gamble pairs such that models considered predict distinct choice vectors across these groups of gamble pairs.

Despite the potential of the present generalization of Bröder and Schiffer’s (2003) strategy classification, a number of limitations remain. For one, there is no way to safely conclude that a classified model actually corresponds to the data-generating cognitive process (Moshagen & Hilbig, 2011). All models are abstractions, and even the best-fitting model may not correspond to underlying processes at all (Roberts & Pashler, 2000). Thus, one cannot say that a participant classified as, say, TTB must have used this strategy. It is merely appropriate to say that TTB is most likely to have generated the data from among the models considered. Although this limitation is certainly not specific to the present method, it seems worthwhile to bear it in mind when applying the method to judgment and decision-making research. Second, it must be acknowledged that the method can distinguish only between models that make different predictions. In the original approach, it was necessary for models to predict different choices across item types or point predictions (such as guessing). With the present generalization, models may also predict different ordering of choice probabilities across item types. Nonetheless, even two models predicting the same choices with the same ordering of choice probabilities may be distinguishable if both make at least one divergent point prediction or predict different upper bounds for the strategy execution error. This will ultimately depend entirely on the models under consideration and item types used, but there certainly is no guarantee that any two models can be distinguished.

Overall, the method extended herein may further broaden researchers’ repertoire for model comparisons in judgment and decision making—most important, allowing for the consideration of psychologically plausible and well-established process models that make probabilistic choice predictions. At the same time, the approach is straightforward, in the sense that all algorithms required are implemented in freely available software.

Appendix

Model equations for each of the strategies considered by Bröder and Schiffer (2003), referring to the item types in Table 1.

WADD (implement with e 1 = e 2 = e 3):

$$ \begin{array}{l}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 1\right)={e}_1\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 1\right)=\left(1-{e}_1\right)\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 2\right)={e}_2\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 2\right)=\left(1-{e}_2\right)\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 3\right)={e}_3\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 3\right)=\left(1-{e}_3\right)\hfill \end{array} $$

EQW (implement with e 1 = e 2 and e 3 = .50):

$$ \begin{array}{l}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 1\right)={e}_1\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 1\right)=\left(1-{e}_1\right)\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 2\right)={e}_2\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 2\right)=\left(1-{e}_2\right)\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 3\right)={e}_3\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 3\right)=\left(1-{e}_3\right)\hfill \end{array} $$

TTB (implement with e 1 = e 2 = e 3):

$$ \begin{array}{l}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 1\right)={e}_1\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 1\right)=\left(1-{e}_1\right)\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 2\right)={e}_2\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 2\right)=\left(1-{e}_2\right)\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 3\right)={e}_3\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 3\right)=\left(1-{e}_3\right)\hfill \end{array} $$

GUESS (implement with e 1 = e 2 = e 3 = .50):

$$ \begin{array}{l}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 1\right)={e}_1\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 1\right)=\left(1-{e}_1\right)\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 2\right)={e}_2\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 2\right)=\left(1-{e}_2\right)\hfill \\ {}p\left(``\mathrm{A}"|\mathrm{Item}\ \mathrm{type}\ 3\right)={e}_3\hfill \\ {}p\left(``\mathrm{B}"|\mathrm{Item}\ \mathrm{type}\ 3\right)=\left(1-{e}_3\right)\hfill \end{array} $$

The multiTree freeware tool (Moshagen, 2010) requires model equations as plain text comprising one row for each equation consisting of three columns (separated by at least one blank character). The first column refers to the item type (see Table 1), the second column specifies the category label, and the third specifies the model equation. The model file for WADD is thus:

1

1A

(1-e1)

1

1B

e1

2

2A

e2

2

2B

(1-e2)

3

3A

(1-e3)

3

3B

e3

All model files can be found in the supplementary material

A corresponding data file is organized as follows:

Data set name

1A

<frequency of option-A choices in item type 1>

1B

<frequency of option-B choices in item type 1>

2A

<frequency of option-A choices in item type 2>

2B

<frequency of option-B choices in item type 2>

3A

<frequency of option-A choices in item type 3>

3B

<frequency of option-B choices in item type 3>