The Iowa gambling task (IGT) has been used in numerous studies to examine decision making, particularly in clinical populations with neuropsychological abnormalities (Bechara, Damasio, Damasio, & Anderson, 1994). The IGT is useful in assessing participants’ sensitivity to potential gains and losses in the environment and their ability to make decisions under uncertainty. The task requires participants to make repeated selections from four decks of cards. Each deck often gives a positive gain in points on each draw, but losses can also be given. Two decks (A and B) are disadvantageous because the cumulative amount lost will exceed the amount gained, and two decks (C and D) are advantageous because the cumulative amount gained will exceed the amount lost (see Table 1). However, the disadvantageous decks always give a higher gain (100 points) than the advantageous decks (50 points), so that participants must learn to avoid the disadvantageous decks because they lead to larger losses, and a poorer cumulative payoff, despite consistently yielding larger gains.

Table 1 Reward schedule for the Iowa gambling task
Full size table

One of the most interesting developments has been the emergence of reinforcement learning (RL) models to quantitatively characterize human behavior in this task (Busemeyer & Stout, 2002; Hochman, Yechiam, & Bechara, 2010; Yechiam, Busemeyer, Stout, & Bechara, 2005). The expectancy valence (EV) model is the predominant RL model that has been fit to IGT data. The EV model has been very useful in examining how different clinical or neuropsychological disorders affect different decision-making processes. For example, Yechiam et al. used the model to identify groups that attend more to gains than to losses (cocaine users, cannabis users, and seniors), attend more to losses than to gains (Asperger’s patients), or attend to only the most recent outcomes (ventromedial prefrontal cortex patients). More recent work has found that another RL model, the prospect valence learning (PVL) model, can provide an even better fit to IGT data than the EV model does, although this model has been used much less extensively (Ahn, Busemeyer, Wagenmakers, & Stout, 2008; Ahn, Krawitz, Kim, Busemeyer, & Brown, 2011). The EV, PVL, and other RL models have been a dominant class of models used to characterize decision-making behavior in numerous studies (Gureckis & Love, 2009a, b; Worthy, Maddox, & Markman, 2007). The basic assumptions underpinning these RL models is that the outcomes of past decisions are integrated to determine expected reward values for each option, and that decision-makers select options with higher expected rewards with greater probability than they select options with lower expected rewards.

However, recent work from our labs has shown that a model that assumes a simple win-stay/lose-shift (WSLS) strategy can often characterize behavior in repeated choice decision-making tasks better than do traditional RL models (Otto, Taylor, & Markman, 2011; Worthy & Maddox, 2012; Worthy, Otto, & Maddox, 2012). The WSLS strategy is fairly straightforward: Participants “stay” by picking the same option on the next trial if they are rewarded (a “win” trial) or switch by picking a different option on the next trial if they are not rewarded (a “loss” trial). In the IGT, Cassotti, Houde, and Moutier (2011) recently attempted to identify WSLS behavior by defining any net outcome on a trial that is greater than or equal to zero as a win, and any net outcome that is less than zero as a loss, allowing the investigators to examine response-switching behavior as a function of net gains versus losses. However, to our knowledge, a formal WSLS model has not been fit to IGT data. The WSLS assumes a different strategy than do RL models in decision-making tasks like the IGT (Worthy et al., 2012), and the prevalence of each type of strategy is an important empirical question that we address in the present work. In the next section, we formally describe the EV, PVL, and WSLS models, as well as our model comparison procedure. We then present the behavioral and modeling results of an experiment that we conducted with healthy young adults who performed the original version of the IGT (Bechara et al., 1994).

EV, PVL, and WSLS models

The EV model assumes that decision-makers maintain an “expectancy” for each deck that represents that option’s expected reward value. After a choice is made and feedback [i.e., points gained—win(t)—and lost—loss(t)] is presented, the utility u(t) for the choice made on trial t is given by

$$ u(t)=w\cdot win(t)-\left( {1-w} \right)\cdot loss(t). $$
(1)

The model has a total of three free parameters. One free parameter represents the degree to which participants weight gains relative to losses (0 ≤ w ≤ 1). Values greater than .50 indicate a greater weight for gains than for losses. The utility of each choice [u(t)] is then used to update the expectancy for the chosen option on trial t using a delta reinforcement learning rule (Yechiam & Busemeyer, 2005):

$$ {E_j}(t)={E_j}\left( {t-1} \right) + \phi \cdot \left[ {u(t)-{E_j}\left( {t-1} \right)} \right]. $$
(2)

The recency parameter (0 ≤ ϕ ≤ 1) describes the weight given to recent outcomes in updating expectancies, with higher values indicating a greater weight to recent outcomes. The predicted probability that deck j will be chosen on trial t, P[G j (t)], is calculated using a Softmax rule (Sutton & Barto, 1998):

$$ P\left[ {G_j (t)} \right] = \frac{{{e^{{\theta (t)\cdot}}}^{Ej(t) }}}{{\sum\nolimits_{j=1 } {^4{e^{{\theta (t)\cdot}}}^{Ej(t) }} }}. $$
(3)

Consistency in choices is determined by the following equation:

$$ \theta (t)={{\left( {\frac{t}{10 }} \right)}^c}, $$
(4)

where c (–5 ≤ c ≤ 5) is the response consistency or exploitation parameter. Positive values of c indicate an increase in the degree to which participants select higher-valued options as the number of trials (t) increases, and negative values of c indicate more random responding over the course of the task.

The PVL model also assumes that participants maintain an expectancy for each deck, but it differs from the EV model as to how the expectancies are computed. The evaluation of outcomes follows the prospect utility function, which has diminishing sensitivity to increases in magnitude and different sensitivities to losses and gains. The utility, u(t), on trial t, of each net outcome, x(t), is

$$ u(t)=\left\{ {\begin{array}{*{20}{c}} {x{{{(t)}}^{\alpha }}\quad \quad \:\text{if}\,x(t)\geqslant 0,} \\ {-\lambda {{{\left| {x(t)} \right|}}^{\alpha }}\:\:\text{if}\,x(t)<0.} \\ \end{array}} \right. $$
(5)

Here, α is a shape parameter (0 < α < 1) that governs the shape of the utility function, and λ is a loss aversion parameter (0 < λ < 5) that determines the sensitivity of losses as compared to gains. If an individual has a value of λ greater than 1, it indicates that the individual is more sensitive to losses than to gains, and a value less than 1 indicates a greater sensitivity to gains than to losses. The PVL model uses a decay reinforcement learning rule (Erev & Roth, 1998) that assumes that the expectancies of all decks decay, or are discounted, over time, and that the expectancy of the chosen deck is added to the current outcome utility:

$$ {E_j}(t)=A\cdot {E_j}\left( {t-1} \right) + {\delta_j}(t)\cdot u(t). $$
(6)

The parameter A (0 < A < 1) determines how much the past expectancy is discounted. δ j (t) is a dummy variable that is 1 if deck j is chosen, and 0 otherwise. The PVL model that we used in the present work utilizes Eq. 3 to determine the probability of selecting each action, along with a trial-independent choice-consistency rule in place of Eq. 4:

$$ \theta (t)={3^c}-1. $$
(7)

Equation 4 assumes trial-dependent consistency in choices, while Eq. 7 assumes trial-independent consistency in choices. We use these versions of the EV and PVL models because they have been used most consistently in previous work (e.g., Ahn et al., 2011; Yechiam et al., 2005).Footnote 1

The WSLS model that we used in the present work has two free parameters. The first parameter represents the probability of staying with the same option on the next trial if the net gain received on the current trial is equal to or greater than zero:

$$ P\left[ {G_j (t) \ \left| {\mathrm{choic}{{\mathrm{e}}_t}_{-1 }={G_j}\&r\left( {t-1} \right)\geqslant 0} \right.} \right]=P\left( {\mathrm{stay}\left| {\mathrm{win}} \right.} \right). $$
(8)

In Eq. 8, r represents the net payoff received on a given trial, where any loss is subtracted from the gain received. The probability of switching to another option following a win trial is 1 – P(stay | win). To determine a probability of selecting each of the other three options, we divide this probability by 3, so that the probabilities for selecting each of the four options sum to 1.Footnote 2

The second parameter represents the probability of shifting to the other option on the next trial if the reward received on the current trial is less than zero:

$$ P\left[ {G_j (t)\left| { \ \mathrm{choic}{{\mathrm{e}}_t}_{-1 }={G_j}\&r\left( {t-1} \right) < 0} \right.} \right]=P\left( {\mathrm{shift} \ \left| {\mathrm{loss}} \right.} \right). $$
(9)

This probability is divided by three and assigned to each of the other three options. The probability of staying with an option following a “loss” is 1 – P(shift | loss).Footnote 3

To address the prevalence of RL versus WSLS strategy use in the IGT, we conducted an experiment in which healthy young adults performed the original version of the IGT (e.g., Bechara et al., 1994), and we fitted the data with the EV, PVL, and WSLS models, along with a baseline (or null) model that prescribes no reactivity to outcomes. To foreshadow the results, we found that approximately half of the participants’ data were best fit by the WSLS model, with the PVL model providing the best fit to about half of the data sets as well. We also present the results of a parametric bootstrap cross-fitting analysis designed to address whether the good fit for the WSLS model is a result of its flexibility in mimicking the EV and PVL models (Wagenmakers, Ratcliff, Gomez, & Iverson, 2004; Worthy et al., 2012). The results of this analysis suggest that the WSLS assumes a strategy different from that assumed by either RL model, with the WSLS and RL models being equally unable to fit data generated by the other model. Finally, we show that behavior predicted from simulations of the WSLS and PVL models more closely aligns with the experimental data than does the behavior predicted from the EV model.

Method

Participants

A group of 41 undergraduate students from Texas A&M University, Commerce, participated in the experiment for course credit (mean age = 21.29 years, range = 18–29; 30 female, 11 male).

Procedure

The participants performed a computerized version of the IGT programmed with the PEBL experiment-building software (Mueller, 2010). Four decks appeared on the screen, and participants selected one deck on each of 100 trials. Upon each selection, the computer screen displayed the card choice, reward, penalty, and net gain beneath the card decks. The total score was displayed on a score bar at the bottom of the screen. Participants were told that they had received a loan of $2,000. Their goal was to maximize their gains and minimize losses. The task was self-paced, and participants were unaware of how many card draws they would receive. The schedules of rewards and penalties were identical to those used in the original IGT (Table 1; Bechara et al. 1994).

Results

Choice behavior

Figure 1 plots the average proportions of draws from each of the four decks in each of five 20-trial blocks of trials. A 4 (deck) × 5 (block) repeated measures ANOVA revealed a main effect of deck. To further examine the main effect of deck, we conducted paired-sample t tests on the proportions of draws from each deck across all trials. We compared the proportions of draws from Decks A and B to the proportion of draws from each of the other decks (five comparisons), as well as comparing the proportions of draws from the advantageous decks (C and D). Thus, we performed a total of six paired-sample t tests. To control for the Type I error rate, we performed a Bonferroni correction and used a significance threshold of .0083 for each pairwise comparison. The only comparison that did not reach significance at this threshold was the comparison between decks C and D, t(40) = –0.10, p > .10. All other comparisons were significant (p < .001 for each comparison). Deck A was selected significantly less often than any of the other decks, Deck B was selected significantly more often than any of the other decks, and Decks C and D were selected equally often.

Fig. 1
figure 1

Average draws from each deck in each 20-trial block in the experiment

Full size image

We also found a significant Deck × Block interaction, F(12, 480) = 3.02, p < .001, \( \eta_p^2=.070 \). To investigate the locus of this interaction, we conducted repeated measures ANOVAs on the proportion of draws for each deck and examined the linear trends. We found significant effects of block for Deck A, F(1, 40) = 31.93, p < .001, \( \eta_p^2=.444 \); Deck C, F(1, 40) = 5.96, p < .05, \( \eta_p^2=.130 \); and Deck D, F(1, 40) = 4.84, p < .05, \( \eta_p^2=.108 \). The effect of block was not significant for Deck B, F(1, 40) < 1, p > .10. Thus, preferences for Decks A, C, and D changed over the course of the task, but preferences for Deck B did not.

Modeling results

To assess which account of choice behavior (RL vs. WSLS) described decision-makers’ behavior better, we fit each participant’s data individually with the EV, PVL, and WSLS models described above. We also fit a three-parameter baseline model that assumed fixed choice probabilities (Gureckis & Love, 2009a; Worthy & Maddox, 2012; Yechiam et al., 2005). The baseline model had three free parameters that represented the probabilities of selecting Decks A, B, and C (the probability of selecting Deck D was 1 minus the sum of the three other probabilities).

The models were assessed on their ability to predict each choice that a participant would make on the next trial, by estimating parameter values that maximized the log-likelihood of each model, given the participant’s choices. We used Akaike’s information criterion (AIC; Akaike, 1974) to examine the fit of each model relative to the fit of the baseline model. AIC penalizes models with more free parameters. For each model i, AIC i is defined as

$$ \mathrm{AI}{{\mathrm{C}}_i}=-2\log {L_i} + 2{V_i}, $$
(10)

where L i is the maximum likelihood for model i and V i is the number of free parameters in the model. Smaller AIC values indicate a better fit to the data. We compared the fits of the EV, PVL, and WSLS models relative to the fit of the baseline model by subtracting the AIC of each model from the AIC of the baseline model for each participant’s data (e.g., Gureckis & Love, 2009a):

$$ Relative Fit(M)=\mathrm{AI}{{\mathrm{C}}_{\mathrm{B}}}-\mathrm{AI}{{\mathrm{C}}_{\mathrm{M}}}. $$
(11)

Positive values indicate a better fit of the learning model, and negative values indicate a better fit of the baseline model.

Table 2 shows the average best-fitting parameter values for each model. The average relative fit for the EV model was only slightly greater than zero (M = 0.58, SE = 1.89), with data from 44 % of participants being fit better by the EV model than by the baseline model. The average relative fit for the PVL model was much higher (M = 24.27, SE = 4.78), with data from 78 % of participants being fit better by the PVL model than by the baseline model, and the average relative fit for the WSLS model was similar to that of the PVL model (M = 23.14, SE = 4.91), with data from 90 % of the participants being fit better by the WSLS model than by the baseline model. The EV model provided the best fit to two of the 41 participants’ data (4.9 %); the PVL model provided the best fit to 17 participants’ data (41.5 %); the WSLS model provided the best fit to 20 participants’ data (48.8 %); and the baseline model provided the best fit to two participants’ data (4.9 %).

Table 2 Average best-fitting parameter values for the EV, PVL, and WSLS models
Full size table

We also examined the proportions of times that participants who were fit best by either the PVL or the WSLS model selected each deck, but there were no significant differences between these groups (for Deck A, PVL = .13, WSLS = .16; for Deck B, PVL = .35, WSLS = .33; for Deck C, PVL = .24, WSLS = .26; for Deck D, PVL = .28, WSLS = .26).

Recent work has demonstrated that model complexity cannot solely be accounted for by measures like AIC or the Bayesian information criterion (Schwarz, 1978) that penalize models for the number of free parameters (Djuric, 1998; Myung & Pitt, 1997), since often models with the same number of free parameters differ in how flexibly they can fit data. Here, the WSLS model may be more flexible than the EV or PVL models, because it can account for a wider range of behavior in decision-making tasks. To address this issue, we used a procedure known as the parametric bootstrap cross-fitting method (PBCF), proposed by Wagenmakers et al. (2004). This method involves simulating a large number of data sets with each of two models and then fitting each data set with each model. If neither model can mimic the other, then the model that generated the data should provide the best fit to the majority of data sets. Performing these cross-fitting analyses between the WSLS and PVL and between the WSLS and EV models allowed us to determine the degrees to which the WSLS model and the RL models assume unique strategies.

For the simulated data sets, we used the parameter values that best fit our participants’ data. For each model, we generated 1,000 data sets using parameter combinations that were sampled with replacement from the best-fitting parameter combinations for participants in our experiment. Thus, for the EV model we randomly sampled a combination of w, ϕ, and θ that provided the best fit to one participant’s data and used those parameter values to perform one simulation of the task. We generated 1,000 simulated data sets in this manner and performed the same simulation procedure with the WSLS and PVL models. We then fit each simulated data set with each model and determined the Relative Fit WSLS value for each data set. For the EV-versus-WSLS comparison, the relative fit of the WSLS model is given by

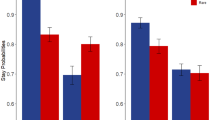
$$ Relative \ Fi{t_{\mathrm{WSLS}\text{-}\mathrm{EV}}}=\mathrm{AI}{{\mathrm{C}}_{\mathrm{EV}}}-\mathrm{AI}{{\mathrm{C}}_{\mathrm{WSLS}}}. $$
(12)

Relative Fit WSLS-PVL was computed by replacing AICEV with AICPVL in Eq. 12. Figure 2A plots the distribution of Relative Fit WSLS-EV values for the data generated by each model. The EV model provided the best fit for 97.0 % of the data sets that were generated by the EV model, while the WSLS model provided the best fit for 97.9 % of the data sets that were generated by the WSLS model. Figure 2B plots the distribution of Relative Fit WSLS-PVL values for data generated by each model. The PVL model provided the best fit for 88.0 % of the data sets that were generated by the PVL model, while the WSLS model provided the best fit for 88.1 % of the data sets that were generated by the WSLS model.

Fig. 2
figure 2

Results of parametric bootstrap cross-fitting. Panel A depicts the distributions of RelativeFit WSLS-EV values for data sets generated by the EV (black) and WSLS (gray) models. Panel B depicts the distributions of RelativeFit WSLS-PVL values for data sets generated by the PVL (black) and WSLS (gray) models. Positive values indicate a better fit for the WSLS model than for either the EV (A) or the PVL (B) model

Full size image

We also examined the average proportions of times that each model selected each deck across the 1,000 simulations for each model, with results plotted in Fig. 3. Interestingly, the EV model predicted that Deck A (M = .26) would be selected more frequently than Deck B (M = .22), whereas human participants and the PVL and WSLS models selected Deck B (M = .34 for the participants, M = .29 for the PVL model, and M = .26 for the WSLS model) more often than Deck A (M = .14 for participants, M = .17 for the PVL model, and M = .21 for the WSLS model), with the PVL model’s predictions most closely aligning with the proportions of times that human participants selected each disadvantageous deck.

Fig. 3
figure 3

Average proportions of draws from each deck by participants and predicted from 1,000 simulations of each model

Full size image

Comparison of high versus low performers

While several studies of IGT performance in healthy young adults have found a high preference for Deck B (e.g., Dunn, Dalgleish, & Lawrence, 2006; Lin, Chiu, Lee, & Hsieh, 2007; Toplak, Jain, & Tannock, 2005), this preference is characterized as a determinant of poor performance in the task (Ahn et al., 2008). To examine how each model fit the data for high and low performers, we performed a median split on the proportions of selections from the good decks, C and D (treating the lower and upper halves as low and high performers, respectively).

The average fits of each model—relative to the baseline model—are shown in Table 3, revealing that the WSLS model provided the best fit to the high performers’ data, while the PVL model provided the best fit to low performers’ data. We compared the relative fits of the WSLS model and the PVL model (Relative Fit WSLS-PVL = AICPVL – AICWSLS) between the high- and low-performing groups. Relative Fit WSLS-PVL values were significantly higher for high performers (M = 3.65, SE = 3.15) than for low performers (M = –6.17, SE = 3.32), t(39) = 2.15, p < .05.

Table 3 Average relative fit values of each model (relative to the baseline model) for high and low performers
Full size table

Table 4 lists the average best-fitting parameter values for each model. The only parameter that differed significantly between the low- and high-performing participants was the EV model’s w parameter, which weights the value of gains compared to losses. High performers’ data (M = .32, SE = .07) were fit best by lower values of w than were low performers’ data (M = .60, SE = .08), t(39) = –2.51, p < .05.

Table 4 Average best-fitting parameter values for high and low performers for the EV, PVL, and WSLS models
Full size table

Discussion

The IGT has perhaps been the task most frequently used to examine decision-making behavior, and RL models, particularly the EV model, have been predominantly used to describe behavior in the task. Our analyses demonstrate that a WSLS model—which assumes that people stay or switch on the basis of whether the net reward is greater than or equal to zero—provides the best fit for about half of the data sets, with the PVL model fitting the other half best. Cross-fitting analyses demonstrated that the WSLS model assumes a strategy unique from those of the EV and PVL models.

When simulated, the PVL and WSLS models selected Deck B more often than Deck A, which was in line with the observed behavior of our participants, but the EV model showed the opposite pattern of behavior. The high preference for Deck B that we observed has been observed in other IGT experiments and is an example of a broader phenomenon in experience-based decision making, whereby people underweight rare events (Barron & Erev, 2003; Barron & Yechiam, 2009). Deck B is an appealing choice in the IGT because it gives a larger gain than Deck C or D (100 points, vs. 50 points for C and D) on each trial and a loss only once in every ten trials (although the loss of 1,250 points is quite large). A participant using a WSLS strategy will “win” on 90 % of the trials, and thus stay with this option much of the time. The PVL model predicted the greatest preference for Deck B—indeed, individuals who selected Deck B more often were fit better by the PVL than by the WSLS model. Intuitively, the PVL model’s decay rule may have allowed it to quickly discount the large but rare losses given by Deck B.

Our results suggest that human behavior in the IGT, a task in which choice has been previously characterized as being guided by an incremental updating procedure computationally instantiated by either the EV or PVL model, may be better characterized as a heuristic-based WSLS strategy for a large proportion of participants. While we fit models that strictly assumed either WSLS or RL strategy use, it is possible that many people use some combination of the two strategies or switch strategies throughout the task. We also only examined behavior in one task. Future work should consider the degree to which the fits of each of these models can be used to predict subsequent decision-making behavior in other tasks (Ahn et al., 2008; Yechiam & Busemeyer, 2008).

In the present work, we only examined decision-making behavior in a group of predominantly female, healthy young adults who were not offered an incentive for good performance. Future work should address how gender and motivation influence strategy use, as well as (a) whether the WSLS and PVL models also characterize the behavior of patient groups better and (b) how differences in parameter values—as demonstrated in applications of the EV model to patient populations—can be brought out in fits of the WSLS and PVL models in order to elucidate deficits in decision making found in these patient groups.