Introduction

A good understanding of rational numbers is of crucial importance for learners’ later mathematical development (e.g., Obersteiner, Reiss, Van Dooren, & Van Hoof, 2019; Siegler et al., 2012; Van Hoof, Vamvakoussi, Van Dooren, & Verschaffel, 2017). To give one example, in a longitudinal study Siegler et al. (2012) found that fifth graders’ rational number understanding predicted their mathematics and algebra scores in high school. This was even found after they had controlled for reading achievement, IQ, working memory, whole number knowledge, family income, and family education. These results are not surprising, given the hierarchically structured development of mathematics on both the cultural (phylogenetic) and individual (ontogenetic) planes (De Corte, Greer, & Verschaffel, 1996).

A good understanding of rational numbers also plays an important role in daily life: reading recipes, calculating prices during sales, etc. (see, e.g., Reyna & Brainerd, 2007). Even though the crucial role of a good rational number understanding for school mathematics and for daily life has been documented amply, and a lot of effort is being put into teaching learners rational numbers, many elementary and secondary school learners, adults, and even (prospective) teachers continue to struggle with many aspects of these kinds of numbers (e.g., Christou, 2015; Depaepe, Torbeyns, Vermeersch, Janssens, Kelchtermans, Verschaffel, & Van Dooren, 2013; McMullen, Laakkonen, Hannula-Sormunen, & Lehtinen, 2015; Siegler et al., 2012; Vamvakoussi, Van Dooren, & Verschaffel, 2012; Van Hoof, Degrande, Ceulemans, Verschaffel, & Van Dooren, 2018). This clearly points to the need to further investigate why fractions are so hard to understand and to reveal which cognitive processes underlie this understanding.

While there may be many reasons why fractions are so hard to grasp (for an overview, see, e.g., Moss, 2005), a vast amount of previous research has shown that a major source of difficulties with rational numbers is the “natural number bias” (for an overview, see Van Hoof et al., 2017). The natural number bias describes the phenomenon of applying natural number knowledge in rational-number tasks where this is inappropriate (e.g., Ni & Zhou, 2005). For example, with regard to the numerical size of numbers, learners have been found to erroneously think that the larger the natural numbers that constitute the fraction are, the larger the numerical value of the fraction is. For example: 7/11 is wrongly assumed to be larger than 4/5, given that 7 is larger than 4 and 11 is larger than 5. Along the same lines, with decimal numbers, learners have been found to erroneously think that the more digits a decimal number has, the larger the numerical value of the decimal number is. For example: 0.16 is wrongly assumed to be larger than 0.4, given that 16 is larger than 4.

Indications for the natural number bias are typically found in higher accuracy levels on fraction tasks where one can use natural-number knowledge to come to the right answer (termed congruent items, e.g., which fraction is the larger one? 7/11 or 3/8; 7 is larger than 3 and 11 is larger than 8; just like 7/11 is larger than 3/8) compared to the lower accuracy levels on fractions tasks in which the use of natural-number knowledge leads to the incorrect answer (termed incongruent items, e.g., which fraction is the larger one? 6/11 or 3/4, 6 is larger than 3 and 11 is larger than 4, however 6/11 is smaller than 3/4) (e.g., Ni & Zhou, 2005; Vamvakoussi & Vosniadou, 2004; Vamvakoussi et al., 2012; Van Hoof, Verschaffel, & Van Dooren, 2015).

When being introduced to rational numbers, there are several aspects in which the rules for natural numbers are no longer necessarily applicable, leading to systematic mistakes. For example, contrary to what happens in the domain of natural numbers, in the rational number-domain multiplication does not always lead to a larger outcome (with fractions smaller than 1; for example 3 * 1/2 is 3/2, which is smaller than 3). Moreover, unlike with natural numbers (which are characterized by a discrete structure), one cannot say which number comes next after a given rational number (as rational numbers are characterized by a dense structure), because there are always infinitely many numbers in between two given rational numbers.

While learners struggle with these and other aspects in which natural and rational numbers differ, previous studies have shown that a first step in learners’ understanding of rational numbers is a good understanding of their numerical size. For example, Van Hoof et al. (2018) longitudinally followed 201 upper elementary school learners in the crucial years of instruction in rational numbers (fourth to sixth grade). Results showed that learners first needed to have a good understanding of the size of fractions before they were able to reason about operations with fractions. Similar results were found in a Finnish sample (McMullen et al., 2015). Alongside the results of these longitudinal studies, Siegler et al.’s integrated theory of numerical development (e.g., Siegler, Thompson, & Schneider, 2011) also points to the crucial role of the understanding of the size of rational numbers. The integrated theory of numerical development states that “although whole numbers and fractions differ in many ways that influence their development, an important commonality is the centrality of knowledge of numerical magnitudes in overall understanding” (Siegler, Thompson, & Schneider, 2011, p. 273). Given the crucial role of a good understanding of fraction magnitude, the present study focuses on the understanding and processing of the magnitude of fractions.

A lot of research investigating the natural number bias starts from the conceptual change perspective (e.g., Christou, 2015; Vamvakoussi et al., 2012; Van Hoof et al., 2018; Vosniadou, 2013). According to this perspective, the construction of a mathematical concept in a learners’ mind is a gradual and time-consuming process, starting from a naïve, intuitive idea of a concept (in our case a number, including fractions) to the mathematically correct concept. This process is characterized by many intermediate states of understanding, given that new (and sometimes incompatible) information is added to the already existing conceptual structures, often leading to inconsistencies and misconceptions (Vosniadou, 2013). The conceptual-change theory offers an explanation for learners’ large and continued struggle with fractions. Given that in the first years of life and in the first years of (mathematics) instruction the only numbers learners encounter are natural numbers, people tend to create a concept of number that is solely based on natural numbers, with accompanying rules and characteristics (e.g., multiplication always increases size). Therefore, a drastic change of the conceptualization of number is necessary to be able to understand rational numbers (e.g., Christou, 2015; McMullen et al., 2015; Vamvakoussi et al., 2012; Vamvakoussi & Vosniadou, 2004; Vosniadou, 2013).

In sum, studies starting from the conceptual-change theory provide a good understanding of learners’ development of a mathematical concept, starting from a naïve, intuitive idea of a concept (in our case number, including fractions) to the mathematically correct concept. Moreover, when a conceptual change has taken place, it does not imply that the initial intuitive idea is gone. The correct concept can coexist with the intuitive concept (DeWolf & Vosniadou, 2015).

This idea is closely related to the dual-process perspective. The dual-process perspective and more specifically the default interventionist theory (e.g., Evans, 2008; but see also, e.g., Pennycook, Fugelsang, & Koehler, 2015, and De Neys, 2017, for critiques on this traditional model) supplements the conceptual-change theory by providing the theoretical and methodological tools to investigate and explain how people who have all the required domain-specific knowledge and skills to solve a certain task can still make mistakes, namely because they are still affected by erroneous intuitive reasoning. More specifically, reaction-time studies have been shown to be useful in shedding light on the intuitive character of learners’ mistakes in several mathematical tasks (see, e.g., Lem et al., 2014; Gillard, 2009).The dual process theory assumes that people have two types of reasoning processes: the first one is termed the intuitive-reasoning process (T1) and the second one the analytic-reasoning process (T2). T1 processing is often characterized as fast, automatic, associative, and undemanding of working-memory capacity, whereas T2 is often characterized as slow, controlled, deliberate, and highly demanding of working-memory capacity. The fast T1-intuitions are presumed to take place spontaneously and also often lead to successful responses to a task. However, fast intuitive reasoning processes can lead to wrong answers to tasks where more extensive, analytical thought processes are necessary. In this case, two outcomes are possible. First, it is possible that an incorrect intuitive reasoning process takes place without intervention by the analytical T2 processing. In this case, the process will lead to a wrong answer. A second possibility is that the analytical T2 processing does intervene, evaluates the intuitively obtained answer, and tries to inhibit it, leading to a different outcome (e.g., De Neys, 2017; Gillard, Van Dooren, Schaeken, & Verschaffel, 2009).

A central claim within the dual-process framework that can be used as a basis to empirically investigate whether an answer is the outcome of an intuitive or an analytic process, is the different speed of processing, given that T1 reasoning is faster than T2 reasoning. Using this dual-process perspective, several studies have shown that participants took more time to correctly solve incongruent fraction tasks than congruent ones. These reaction-times studies suggest that analytical reasoning takes place when one is solving an incongruent fraction item correctly, and therefore that the natural number bias has an intuitive character (e.g., Obersteiner, Van Dooren, Van Hoof, & Verschaffel, 2013; Vamvakoussi et al., 2012; Van Hoof, Lijnen, Verschaffel, & Van Dooren, 2013). A fundamental limitation of these studies, however, is that they are exclusively correlational in nature. The causal relation between slower, analytical processing and correctly solving incongruent items has not been investigated yet. Although it has been shown that a correct response to an incongruent item is associated with longer reaction times, this does not allow the conclusion that shorter reaction times decrease the chance of solving incongruent items correctly (De Neys, 2006).

It is important to note that in the research literature many different definitions of intuition and intuitive reasoning exist. There is, however, a broad agreement that “intuition is some kind of information acquired without conscious, deliberative reasoning” (Epstein, 2010, p. 296). In the present study we define intuitive reasoning as fast, automatic, and undemanding of working-memory capacity, which is in line with the dual-process theory of reasoning and more specifically the default interventionist theory (e.g., Evans, 2008). It should be noted, however, that some scholars have raised additional characteristics of intuitive reasoning. Fischbein (1987), for example, stated that intuitions are characterized by self-evidence, intrinsic certainty, immediacy, etc. Epstein’s (2010) cognitive-experiential self-theory also gives a prominent role to human affect in intuitive reasoning (e.g., Epstein, 2010).

The present study

In the present study we examined whether the natural number bias has an intuitive character, starting from the dual-process claim that intuitive responses take less time than analytical responses. As we noted, previous studies using chronometric comparisons of different response types already found that answering correctly on congruent items takes less time compared to answering correctly to incongruent items (e.g., Babai, Levyadun, Stavy, & Tirosh, 2006; Vamvakoussi et al., 2012). Relying on dual-process assumptions that differentiate between intuitive and analytic processes, this suggested that the process in which the natural number bias manifests itself can be characterized as intuitive (e.g., Van Hoof et al., 2013). The present study aimed to address several shortcomings of previous work. First, by experimentally manipulating the allotted response time, we looked for causal evidence for the intuitive nature of the natural number bias. The advantage of using time restriction is that it not only allows us to investigate whether longer reaction times are found on correctly solved incongruent compared to congruent trials, but it also allows us to investigate whether more intuitive responses are given on a fraction-comparison task under time restriction compared to when participants have all the time they need to solve the fraction comparisons. Compared to purely chronometric comparisons, this experimental manipulation has the advantage that it may yield stronger evidence for the intuitive character of the natural number bias (Gillard, 2009).

Second, an additional limitation of correlational reaction-time studies is that one can reasonably assume that participants, for example in classroom cultures with high demands (classrooms in which students feel the pressure to have the highest possible accuracy level on all tests given), may take much more time than actually needed to solve the items, just to be sure that their answers are correct (e.g., double-checking the answer). This behavior can sometimes lead to very long reaction times, noisy data (as not all learners may show this behavior to the same extent, and time needed for double-checking may vary between learners), and ceiling levels in accuracy on all types of items, masking possible effects such as the natural number bias. To check whether this was the case in the present study, we analyzed the data of the participants who scored ceiling levels (100% accuracy) on both congruent and incongruent items separately to investigate whether a time restriction would lead to similar results as compared to the whole sample.

Third, as far as we know, previous studies used time restriction based on median reaction times calculated on a group level to investigate intuitive responses (e.g., Gillard et al., 2009). This might be problematic, given that large individual differences are found in people’s cognitive processes and general reaction speed (e.g., Friedman et al., 2008). Therefore, in the present study optimal time restriction was calculated for each participant separately based on the median reaction time each individual needed to correctly solve congruent items during the first measurement point.

Research questions

The present study addressed four research questions. The first research question was whether we could find the natural number bias in participants’ accuracy and reaction-time data when there is no time restriction (= research question 1). Our hypothesis was that the natural number bias would be found in participants’ reaction times (longer reaction times on correctly solved incongruent items compared to correctly solved congruent items), but not in their accuracy: given that our sample comprised adults, high accuracies were expected on both congruent and incongruent items (Vamvakoussi et al., 2012; Van Hoof et al., 2013). As a result, the natural number bias could be reasonably expected only in participants’ reaction-time data. As stated above, we will separately investigate whether a natural number bias can be found in the reaction times of the subgroup of participants who score 100% on all items at time 1.

The second research question of the present study was whether the natural number bias has an intuitive character (= research question 2). According to the dual-process perspective, when there is limited time to answer a certain task, the analytical reasoning process will be less likely to intervene, leading to more intuitive responses compared to when there is no time restriction. Therefore, we hypothesized that if the natural number bias does indeed have an intuitive character, restricting responding time would lead to an increase in intuitive natural number-based answers and thus in a decrease in correct answers on incongruent items, while correct answers to congruent items would not be affected, or significantly less so, since intuitive responding leads a learner to the correct answer in such items. As with research question 1, we also investigated whether evidence for the intuitive character of the natural number bias can be found in the subgroup of participants who score 100% on all items at time 1.

Conditional on confirmation of the second hypothesis, a third research question was whether participants would detect a conflict between their intuitive natural number-based answer and the correct answer when they fail to compare an incongruent fraction comparison item correctly (= research question 3). Dual-process studies on logical reasoning have indicated that reasoners whose logical inferencing is “biased” by erroneous intuitions often show some minimal error or conflict sensitivity (e.g., De Neys & Glumicic, 2008; Frey, Johnson, & De Neys, 2018; see De Neys, 2014, for a review). For example, these studies typically contrast processing latencies on incorrectly solved incongruent items and correctly solved congruent items. If reasoners do not detect that their incorrect responses to incongruent tasks conflict with the logically appropriate response, their processing time should not differ from the congruent problems in which there is, by definition, no conflict. Results indicate that incorrect responders typically take slightly longer to answer the incongruent than the congruent problems. We applied the same logic in our fraction task to explore participants’ fraction-error sensitivity. By comparing participants’ reaction times on correctly solved congruent items and incorrectly solved incongruent items, we tried to shed light on this research question. If the reaction time on incorrectly solved incongruent items is comparable to congruent items, this would mean that no conflict detection has taken place and the error goes unnoticed. On the other hand, if the reaction times on incorrectly solved incongruent items are higher than on correctly solved congruent items, this points to some minimal conflict sensitivity.

A fourth and final research question concerned the nature of this conflict-detection process. If conflict sensitivity is observed, does it result from analytic thinking or not? (= research question 4). Given that we collected data under time restriction, we were able to answer this question. As explained above, the time restriction gave participants enough time to respond, but not enough time for analytical processes to take place. Therefore, if the reaction times on incorrectly solved incongruent items are still higher than on correctly solved congruent items even under time pressure, this would not only indicate that the participants detect conflict, but that this conflict detection has an intuitive nature. If people detect conflict because of an analytic reasoning process, we would not expect to observe it under time restriction.

Method

Participants

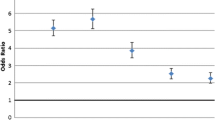
Since our study required that participants had a good understanding of fractions, we decided to collect data with adults. In total, 55 Flemish adults volunteered to participate in this study (mean age = 26.85 years, SD = 7.62). Thirteen participants were pre-service teacher students in their second year of a 3-year Bachelor’s course. These students had already followed a course on the conceptual knowledge of rational numbers. The other 42 participants were adult volunteers with at least a Bachelor’s degree and with various study backgrounds and ages. Of course, all participants were taught extensively about rational numbers during their schooling career in elementary and secondary education. As can be seen in Fig. 1, at time 1, when there was no time restriction to respond to the fraction comparison items, the accuracy levels were very high (mean accuracy of 98.05% on congruent and 95.58% on incongruent items), indicating a good understanding of the numerical size of fractions. All participants signed informed consent and data were collected according to the ethics guidelines of the  KU Leuven.

Fig. 1
figure 1

Participants’ accuracy scores on congruent (CO) and incongruent (IC) items without time restriction (T1) and with time restriction (T2). Vertical stripes indicate the mean score

Full size image

Materials

To investigate people’s processing of the magnitude of fractions, participants solved a fraction-comparison task (FCT), which consisted of 70 fraction-comparison items. Every item contained two fractions that were shown simultaneously on a computer screen, using the E-prime software. Participants had to select the fraction with the largest numerical size by pressing the corresponding key on the keyboard, i.e. “F” if the largest fraction appeared on the left side of the screen and ”J” if the largest fraction appeared on the right side of the screen. Participants were encouraged to answer as accurately and quickly as possible. To investigate the presence of a natural number bias, a distinction was made between congruent and incongruent items. Congruent items are items in which natural number-based responding leads to a correct answer, while incongruent items are items in which natural number-based responding leads to an incorrect answer. In total, there were 14 congruent items, i.e., items where the two fractions had the same denominator (e.g., 6/13 vs. 9/13; 9/13 is larger than 6/13 just like 9 is larger than 6); 14 incongruent items, i.e., items where the two fractions had the same numerator (e.g., 8/11 vs. 8/17, 8/11 is larger than 8/17 although 11 is smaller than 17); and 42 buffer items where the two fractions had no common components (e.g., 11/23 vs. 18/31).

It should be noted that all buffer items can be defined as congruent (e.g., 11/23 vs. 18/31) or incongruent (e.g., 14/25 vs. 18/39) with natural number reasoning. However, recent studies (see, e.g., Gomez, Silva, & Dartnell, 2017) showed that a subgroup of learners use the strategy of “gap thinking” when solving fraction-comparison tasks, namely comparing the absolute difference between numerator and denominator in both fractions and concluding that the largest fraction is the one with the smallest difference. The gap strategy has a different effect on FCTs with and without common components: while the gap strategy always leads to the correct answer in fractions with common components, this is not the case for fractions without common components. More specifically, for FCTs without common components, all incongruent tasks can be solved accurately with the gap-thinking strategy, while this is not true for congruent FCTs without common components. Some of these latter tasks can be solved accurately with the gap-thinking strategy, while others cannot. For example, for the congruent item “28/43 versus 18/37,” gap thinking will lead one to choose the correct alternative, but for another congruent item such as “11/23 vs. 18/31,” gap thinking will lead one to choose the incorrect alternative. Given this different effect of gap-strategy use on distinct tasks without common components, we considered them as buffer items, the goal of which was to minimize possible learning effects during the test.

The FCT item set was further controlled for the distance effect (the mean distance between fractions in each type of comparison tasks was comparable; all between 0.153 and 0.176), benchmarking to 0 (fractions were all above 0.2), benchmarking to 1 (fractions were all below 0.8), benchmarking to 1/2 (in each type of FCT half of the items were characterized by the fact that both fractions were on the same side of 1/2 (both below or above 1/2), while the other half were characterized by the fact that one fraction was below 1/2 and one fraction was above 1/2). Moreover, in half of the items, the largest fraction was on the left side of the screen, while in the other half the largest fraction was on the right side of the screen. At last all fractions were below 1 and no simplifiable fractions were included.

Participants solved the FCT twice. Since the FCT is quite a demanding task and we wanted to control for a possible learning effect, participants were tested on two different days, with at least 1 week in between. During the first testing day, there was no time restriction. During the second testing day, a time restriction was applied. Optimal time restriction was calculated for each individual separately, based on the median reaction time (s) he needed to correctly solve congruent items (where intuitive reasoning leads to the correct answer) during the first measurement point. Large individual differences were found in participants’ median reaction time needed to correctly solve congruent items at time 1 (mean = 2,492.85 ms, SD = 1,204.38, range: 6,319.50).

Participants were informed that, with each trial, a countdown clock on the computer screen would indicate how much time they still have left to answer. If no response was given within the available time or if a response was only given after the time limit, this trial was not included in the data analysis.

Results

To answer the first research question, a paired-samples t-test was conducted comparing participants’ accuracy scores on congruent versus incongruent items when there was no time restriction. Although accuracy was generally very high, a significant difference in the expected direction was found in the scores on congruent (M = 98.05%; SD = 3.37) and incongruent items (M = 95.58%, SD = 7.59); t(54) = 2.31, p = .03, d = 0.31. If we looked at the individual accuracies, we saw that there were 27 participants (49%) who obatined perfect accuracy scores (100%) on both congruent and incongruent items and showed no natural number bias at all in their accuracy scores when there was no time restriction. As stated above, it might have been that this subgroup of participants took more time than needed to compare the fractions, just to be sure that they answered correctly, which could have led to very long reaction times and noisy data. We analyzed the reaction-time data and the effect of time restriction on this subgroup separately (see below).

Next, we looked at participants’ reaction times. Participants’ median latencies were used, given that these are less affected by outliers. To investigate whether a natural number bias could be found in participants’ median reaction times on correctly solved trials, a paired-samples t-test was conducted. When there was no time restriction, significantly lower median reaction times were found on correctly solved congruent items (M = 2,492 ms; SD = 1,204) compared to correctly solved incongruent ones (M = 4,090 ms, SD = 4,651); t(54) = -2.56, p = .01, d = 0.35. The same result was found in the subgroup of participants who showed no natural number bias (i.e., those who had ceiling accuracy levels on both congruent and incongruent items) in their accuracy levels when there was no time restriction. Also in this group (n=27), a significant difference could be found in the median reaction times between correctly solved congruent items (M = 2,063 ms; SD = 579) and correctly solved incongruent ones (M = 2,868, SD = 1,129); t(26) = -5.69, p < .001, d = 1.09.

To answer the second question, we looked, first, at whether time restriction led to an increase in natural-number based answers and thus to a decrease in correct answers on incongruent items, and, second, whether correct answers to congruent items were not, or at least were significantly less, affected by the time restriction since intuitive reasoning leads a learner to the correct answer in such items. In the following analysis on participants’ processing times, all trials where no response was given were removed from the data analysis (n = 80, 5.2% of total trials). First, a paired-samples t-test was conducted to compare participants’ accuracy scores on the incongruent items without and with time restriction. As expected, significantly higher accuracy levels on the incongruent items were found when there was no time restriction (M = 95.58%; SD = 7.59) compared to when there was a time restriction to solve the FCT (M = 76.34%, SD = 18.23); t(54) = 7.69, p < .001, d = 1.04. Second, we investigated the effect of the time restriction on congruent items. A paired-sample t-test was conducted to compare participants’ accuracy scores on the congruent items without and with time restriction. Significantly higher accuracy levels on the congruent items were found when there was no time restriction (M = 98.05%; SD = 3.75), compared to when there was a time restriction (M = 89.73%, SD = 9.49); t(54) = 6.40, p < .001, d = 0.86. Third, we investigated whether the effect of the time restriction was different for congruent compared to incongruent items. A paired-samples t-test was conducted comparing participants’ accuracy decrease between the condition without time restriction (T1) and the condition with time restriction (T2) on congruent (accuracy congruent items T1 – accuracy congruent items T2) versus incongruent items (accuracy incongruent items T1 – accuracy incongruent items T2). Results showed that the accuracy decrease under time restriction was significantly larger on incongruent (mean difference score = 19.25, SD= 18.57) than on congruent items (mean difference score = 8.32, SD = 9.64); t(54) = -4.33, p < .001, d = .58 (see Fig. 1).

Next, we zoomed in on the data of the 27 participants who scored ceiling levels at time 1 on both congruent and incongruent items separately, to investigate whether a time restriction in this group would also lead to a larger performance decrease on incongruent than on congruent items. First, a paired-sample t-test showed significantly higher accuracy levels on incongruent items when there was no time restriction (M = 100%; SD = 0) compared to when there was a time restriction (M = 76.11%; SD = 18.36); t(26) = 6.76, p < .001, d = 1.30. Second, a paired-sample t-test also showed that on congruent items significantly higher accuracy levels could be found when there was no time restriction (M = 100%; SD = 0) compared to when there was a time restriction (M = 90.07%; SD = 8.77); t(26) = 5.89, p < .001, d = 1.13. Results showed that scores decreased significantly more on incongruent (mean difference score = 23.89, SD = 18.36) versus congruent items (mean difference score = 9.93, SD = 8.77) under time restriction; t(26) = -4.05, p < .001, d = .78.

We were unable to answer the third research question, given the ceiling levels when there was no time restriction on both congruent and incongruent items (only six participants made more than one mistake). Since there were lower accuracy levels under time restriction, we were, however, still able to look at whether there was a conflict detection, and, moreover, what the nature of this possible conflict detection was in fraction comparison tasks (research question 4). As previously explained, the time restriction gave participants enough time to respond, but not enough time for analytical processes to take place. Therefore, if the reaction times on incorrectly solved incongruent items were significantly higher than on correctly solved congruent items, this would not only indicate that the participants detected conflict, but that this conflict detection had an intuitive nature. Logically, only participants who made mistakes on incongruent trials were included in the data analysis. Results showed a significant difference in the reaction times on correctly solved congruent (M = 1364; SD = 526) and incorrectly solved incongruent items (M =1,575, SD = 1,059); t(49) = -2.28, p = .03, d = 0.32, when there was a time restriction, indicating the intuitive nature of the conflict detection.

Discussion

The main purpose of the present study was to provide causal evidence for the fact that the natural number bias has an intuitive character. Previous studies (Obersteiner et al., 2013; Vamvakoussi et al., 2012; Van Hoof et al., 2013) already showed that adults need more time to correctly solve fraction tasks that are not in line with their knowledge of natural numbers compared to fraction tasks in which natural number responding leads to a correct answer. These findings already gave some indication that analytical processes might be needed to correctly solve incongruent items, or, in other words, that the process in which the natural number bias manifests itself can be characterized as intuitive. An important limitation of these previous studies, however, was their correlational nature. Although it was found that longer reaction times accompany correctly solved incongruent compared to correctly solved congruent fraction tasks, this does not necessarily imply that longer processing times are necessary to correctly solve incongruent items. In other words, this does not provide causal evidence for the intuitive character of the natural number bias (De Neys, 2006). The present study addressed this limitation using the experimental manipulation of time restriction. Four research questions were raised.

In the first question we looked for traces of the natural number bias in learners’ accuracy and reaction-time data when there was no time restriction. A clear indication for the natural number bias was found both in participants’ accuracy levels and in their reaction-time data at time 1. In general, participants had significantly higher accuracy levels on congruent compared to incongruent fraction comparison tasks. However, about half of them had perfect accuracy on both task types. Further, participants took significantly more time to correctly solve incongruent compared to congruent fraction comparison tasks, and this was also the case for participants with perfect accuracy, showing traces of the natural number bias.

The second research question was about the intuitive nature of the natural number bias. Results showed that time restriction at time 2, or in other words, excluding the involvement of analytical reasoning processes, led to a general decrease of accuracy levels, on both congruent and incongruent items. However, importantly, it was found that participants’ accuracy levels decreased significantly more on incongruent items than on congruent items under time restriction, showing the intuitive character of the natural number bias. A strength of the current study was that, by including the time restriction, we provide experimental evidence for the former correlational result. Time restriction also allowed us to control for the fact that some effects (like the natural number bias) might be masked in participants who take much more time than actually needed to compare fractions, just to be sure that their answers are solved correctly. We checked whether this was the case by separately analyzing the data of the participants who scored perfectly on both congruent and incongruent items at time 1. Results show that also in this subgroup a time restriction led to a larger performance decrease on incongruent items compared to congruent items. So, while in previous correlational studies, and also in our data without time restriction, no effect of the natural number bias could be found in these participants’ accuracy scores (only in their reaction-time data), a clear natural number bias could be found in their accuracy scores under time restriction.

High accuracy levels in the condition without time restriction made the data from this condition useless for answering the question of whether participants detect a conflict between their intuitive natural number-based answer and the correct answer when they incorrectly solve an incongruent fraction comparison item (question 3). However, the data of the condition with time restriction still allowed us to answer this question, as well as the fourth research question about the nature of this conflict detection process. Results showed that participants not only experienced a conflict detection, but moreover that this conflict detection was possible when analytic reasoning was experimentally “knocked out.” That is, even under time restriction we observed significantly faster reaction times on correctly solved congruent compared to incorrectly solved incongruent items. So, even when experimentally preventing people from reflecting by using analytical reasoning processing (through the use of time restriction), the present study showed that they still experience a conflict and notice that something is wrong (they are still slower on wrongly answered incongruent trials compared to correctly answered congruent trials). This indicates that the conflict-detection process is intuitive and not analytic in nature. Interestingly, this fits with conflict-detection studies in the reasoning field that also observed that even after experimentally eliminating analytical T2 reasoning (e.g., by time restriction) conflict detection is still preserved (e.g., De Neys, 2017; Johnson, Tubau, & De Neys, 2016). In other words, although somewhat speculative, our data suggest that two competing intuitions are cued when adults are solving fraction comparison tasks. First, there is an intuition of number that shares the properties of natural numbers, while second there is an intuition of number that shares the properties of rational numbers and is therefore more closely related to the mathematically correct idea of number.

This result is in line with the “hybrid model” within the dual-process literature, which is a recent revision of the traditional default interventionist model (De Neys, 2017). While the default interventionist model assumes that conflict detection takes place through analytical system 2 intervention, the hybrid model postulates that conflict detection can also occur intuitively, resulting from two competing intuitions (e.g., Bago & De Neys, 2017; Pennycook et al., 2015). For example, Pennycook et al. (2015, p. 34) state that “multiple Type 1 processes may be cued by a stimulus (Stage 1), leading to the potential for conflict detection (Stage 2). If successful, conflict detection leads to Type 2 processing (Stage 3), which may take the form of rationalization (i.e., the Type 1 output is verified post hoc) or decoupling (i.e., the Type 1 output is falsified).”The finding of two kinds of intuitions is, moreover, in line with Fischbein’s (1987) work on primary and secondary intuitions. Primary intuitions are developed independently of instruction, but through personal experience. However, when getting instruction on the same concept, other intuitions – called secondary intuitions – may be created. In the present study the intuitive idea of number that shares the properties of natural numbers is a primary intuition, while the intuitive idea of number that shares the properties of rational numbers is a secondary intuition.

We now turn to some implications that emerge from the study. The present study shows that after years of education (on fractions) people still sometimes make (natural number-based) mistakes on fractions, but, at the same time, also intuitively activate the correct fraction knowledge. However, the natural number-based intuition might be stronger and people might not always be able to inhibit the intuitive natural number-based answer. This implies that inhibitory processes might play an important role in the understanding of fractions. In recent years, there has been a promising and rapidly growing research field on the role of inhibition, i.e., the ability to suppress unnecessary distracting information and undesirable answers, as a critical aspect of learners’ cognition and development. Research on the role of inhibition is, moreover, especially important in the research field of cognitive psychology and mathematics (see the Special Issue entitled ‘Inhibitory control in mathematical thinking, problem solving and learning’ (Van Dooren & Inglis, 2015). However, until now, the notion of inhibition was mostly investigated in relation to mathematical achievement in general using correlational studies, leaving the causal relation between inhibition and (specific components of) mathematics, such as fraction understanding, uninvestigated (Van Dooren & Inglis, 2015; Gilmore, Keeble, Richardson, & Cragg, 2015 ). Future research is needed to investigate the possible crucial role of inhibitory control in learners’ understanding of fractions.

Further, since rational number understanding is skill-based and a clear difference can be found in the understanding of fractions of novices and educated adults, future research should investigate whether the same pattern of results can also be found in elementary school children who are starting their instruction in the rational number domain.

As stated by Gillard (2009), the dual-process framework was not developed with the aim of having great implications for (mathematics) education. However, this theoretical framework and its methodologies may reveal important insights for (mathematics) education. There is a crucial difference between mistakes coming from a learners’ misconception on the subject and a mistake coming from an intuitive response (e.g., Gillard, 2009; Leron & Hazzan, 2009). Learners’ tendency to over-use natural number-based strategies to solve fraction tasks calls for a different instructional approach when this tendency is caused by the misconception that rational numbers follow the same rules as natural numbers or when the origin of the tendency is that learners do have a good understanding of fractions but are unable to inhibit their intuitive natural number reasoning. In the former case, much more consideration should go to addressing learners’ misconceptions of rational numbers, with clear attention given to both the similarities and the differences between natural and rational numbers. In the latter case, learners should be made aware of their natural number-based intuitions and more attention should go for example to taking time to double-check the answer.