Accurately predicting what others know is crucial to thriving in a social environment. Teachers who can accurately judge how challenging information is can effectively tailor their pedagogy to support student learning (Sadler, Sonnert, Coyle, Cook-Smith, & Miller, 2013). Politicians and advertisers who can predict what audiences will understand can successfully craft persuasive messages. Estimating others’ knowledge is “indispensable to human social functioning” (p. 85; Nelson, Kruglanski, & Jost, 1998). Here, based in Thomas and Jacoby (2013), I will present a cue-utilization framework that posits estimates of others’ knowledge are produced by weighing a variety of available and salient cues, and I will test that theory across three experiments. I will first outline two existing theories of knowledge estimation (knowledge estimation as static knowledge and knowledge estimation as anchoring and adjustment) before detailing the proposed theory of knowledge estimation as cue utilization.

Theories of knowledge estimation

Knowledge estimation as static knowledge

The traditional view of knowledge estimation suggests that we acquire static facts about what others know through interactions with others. As we gain experience in interacting with others about specific ideas, we develop an understanding of others’ knowledge. In this theory, our estimates of others’ knowledge should not be affected by the contexts or conditions under which the judgments are elicited, but should change as others reveal novel evidence about their knowledge. The view of knowledge estimation as static knowledge has a strong history in education research, in which it is theorized that teachers’ ability to predict students’ knowledge improves through direct teaching experience and interactions with students (Shulman, 1986). Teachers’ abilities to estimate students’ knowledge is grouped into a broader category of pedagogical content knowledge (PCK), which only changes through interactions with students, training in subject matter, teacher education programs, and critical reflection (Magnusson, Krajcik, & Borko, 1999; Shulman, 1986). Some empirical support for this view exists. When instructors teach topics they are unfamiliar with, for example, they struggle to anticipate student problems, fail to predict student misconceptions, and have trouble understanding what will be difficult or easy for students (Driel, Verloop, & de Vos, 1998). Other research echoes the importance of experience and content knowledge for the development of knowledge about what others know (Clermont, Borko, & Karjcik, 1994; Driel et al., 1998; Sanders, Borko, & Lockard, 1993; Smith & Neale, 1989).

However, this traditional view of knowledge estimation as an accumulation of static facts does not adequately explain how estimates of others’ knowledge across domains are systematically biased toward our own knowledge (see Nickerson, 1999, for a review). Similarly, teachers systematically overpredict student performance across a variety of age levels and domains (Berg & Brouwer, 1991; Friedrichson et al., 2009; Goranson, described in Kelley, 1999; Halim & Meerah, 2002; Sadler et al., 2013).

Knowledge estimation as anchoring and adjustment

The second view of knowledge estimation is the anchoring-and-adjustment model, which stems from research in perspective taking during language production (Epley & Gilovich, 2001; Horton & Keysar, 1996; Keysar, Barr, Balin, & Brauner, 2000; Nickerson, 2001). In the anchoring-and-adjustment model of perspective taking (Nickerson, 1999), people adopt others’ perspectives by initially anchoring in their own perspective and subsequently accounting for differences in perspective. The first step of the process (i.e., anchoring) is egocentric, context-independent, and automatic, whereas the second step (i.e., adjustment) involves effortfully and dynamically monitoring perspectives (Horton & Keysar, 1996; Keysar et al., 2000; Keysar, Lin, & Barr, 2003). When using anchoring and adjustment, one’s own knowledge is autonomously activated, and learners must inhibit it to take others’ perspectives (Barr, 2008; Brown-Schmidt, 2009).

Anchoring and adjustment has successfully predicted that one’s own perspective influences estimates of others’ perspectives across a variety of different tasks, including message formation (Epley, Keysar, Boven, & Gilovich, 2004) and mnemonic cue generation (Tullis & Benjamin, 2015). When estimating others’ knowledge, people’s predictions are influenced by their own knowledge: When people know the answer to a question, they predict that a greater number of other people will know the answer than when they do not know the answer (Fussell & Krauss, 1992; Kelley & Jacoby, 1996; Nickerson, Baddeley, & Freeman, 1987). People struggle to ignore their own idiosyncratic knowledge when anticipating the knowledge of others, a general finding that has been labeled the “curse of knowledge” (Birch, 2005; Birch & Bloom, 2003).

Research has also shown that adjusting away from one’s perspective is effortful and time-consuming. For example, people are less likely to adjust their perspectives to consider others’ views when they are distracted (Lin, Keysar, & Epley, 2010), have little incentives to do so (Epley et al., 2004), or are under time constraints (Epley et al., 2004). Further, one’s inhibitory control is related to accuracy in perspective taking because people must inhibit the automatic anchoring in their perspective (Brown-Schmidt, 2009).

Anchoring-and-adjustment theories posit that anchoring in one’s “model of own knowledge” (Nickerson, 1999) is automatic, and that the adjustment process is dynamic. Yet this model fails to detail how the model of one’s own knowledge is created or known: Its automatic nature implies ideas of “direct access” to self-knowledge, in which people monitor the trace strength of their own memories (see Arbuckle & Cuddy, 1969; Cohen, Sandler, & Keglevich, 1991; King, Zechmeister, & Shaughnessy, 1980; Schwartz, 1994). Direct access theories of self-knowledge have significant trouble explaining a wide variety of results in how people estimate their own knowledge, particularly with respect to conditions in which predictions of self-knowledge are dissociable from actual performance (see Benjamin, 2003; Dunlosky & Nelson, 1994; Finley, Tullis, & Benjamin, 2009; Tullis & Benjamin, 2011). Further, recent research in knowledge estimation suggests that the degree to which people’s estimates of others’ knowledge are based in their own are influenced by how those judgments are elicited. More specifically, the presence of the correct answer reduces reliance on one’s egocentric perspective during knowledge estimation (Kelley & Jacoby, 1996; Thomas & Jacoby, 2013). Research suggests that there are differences in predictions of others’ knowledge without corresponding differences in adjustment processes, which is a challenge to the idea that anchoring in one’s own perspective is an automatic and necessary first step to predict others’ knowledge.

Knowledge estimation as cue utilization

Building off Koriat (1997) and Thomas and Jacoby (2013), I propose a third theory of knowledge estimation as cue utilization. In this view, judging others’ cognition is qualitatively the same as judging one’s own cognition: People infer metacognitive judgments from a variety of relevant and available cues (Bem, 1972; Koriat, 1997; Nelson et al., 1998). Koriat (1997) outlines different kinds of cues that may be used to infer one’s own cognition, including intrinsic (i.e., cues related to the inherent difficulty of the stimuli), extrinsic (i.e., cues related to how the stimuli were studied), and mnemonic cues (i.e., cues related to one’s individual mnemonic processing). The relevant and available cues used for judging knowledge may change based upon the stimuli, the specific judgment conditions, and the person under judgment. The anchoring-and-adjustment model says that one’s own knowledge must serve as the initial basis for estimates of others’ knowledge; alternatively, the cue-utilization model posits that one’s own knowledge may serve as a cue about what others know, but anchoring in one’s knowledge is neither automatic nor necessary. In fact, judgment conditions may preclude people from accessing their own knowledge or using their own knowledge to predict others’ knowledge (see Dunlosky & Nelson, 1994). Further, the judge may utilize some metacognitive cues and ignore others depending on the judge’s beliefs about the cues’ diagnosticity. For example, if the judge is a chemistry expert, the judge’s solution time related to chemistry problems may not accurately reflect the broader population’s abilities and knowledge of chemistry; therefore, the judge may largely ignore consideration of her own knowledge in such a situation.

Under many conditions, similar cues may be used to estimate one’s own knowledge and others’ knowledge. For example, familiarity with the question and answer may drive estimates of knowledge for self (Metcalfe, Schwartz, & Joaquim, 1993; Reder, 1987) and for others (Tullis & Klein, 2018). Alternatively, there may be cues that people could use to infer others’ knowledge that they would not utilize when inferring their own knowledge. Jost, Kruglanski, and Nelson (1998) specified that people could use generalized statistical knowledge about what people know and personal interactions with the target individual when predicting others’ cognitions. The cue-utilization framework, then, easily accounts for the effects suggested by the model of knowledge estimation as static knowledge: prior interactions with target students can serve as one of many cues used to estimate others’ knowledge. Further, as in anchoring and adjustment, one’s own mental processes can serve as one of the many cues people use to estimate others’ knowledge.

Cue utilization also shows how the accuracy of metacognitive judgments for others can shift based upon the availability of different metacognitive cues. For example, the accuracy of mnemonic predictions about others improves significantly when cues about the specific people’s experiences become available to the judges (Jameson, Nelson, Leonesio, & Narens, 1993; Vesonder & Voss, 1985). In fact, recent research suggests that the primary decrement to predicting others’ memories is a lack of cues related to others rather than the interfering influence of one’s own experience (Tullis & Fraundorf, 2017). Further, when predicting others’ knowledge, exposure to the correct answer of a problem or anagram causes people to rely less on their own knowledge and more on item difficulty (Thomas & Jacoby, 2013) or analytic theories of difficulty (Kelley & Jacoby, 1996). Similar results occur when people assess their own learning: eliciting judgments of learning (JOLs) when the presence of the cue and the target prevents diagnostic retrieval attempts of the target from their own memories and forces people to rely upon other (less diagnostic) metacognitive cues, like target familiarity (Dunlosky & Nelson, 1994; Nelson & Dunlosky, 1991).

Experiments

The current experiments test the central predictions from the knowledge estimation as cue-utilization framework by examining whether judgments about others’ knowledge change based upon the how those judgments are elicited. Knowledge estimation as static facts suggests that the same estimates of others’ knowledge should be elicited regardless of judgment conditions because knowledge estimation is based upon static facts about what others know. Anchoring and adjustment suggests that estimates of others’ knowledge must be automatically based in one’s own knowledge, and the only changes in estimates should occur through differential adjustment processes. Cue utilization posits that judgment conditions could shift the types of cues that are available to judges and therefore should alter their estimates of others’ knowledge. More specifically, judgment conditions that promote accessing one’s own knowledge should lead to estimates of others that are more strongly tied to one’s mnemonic processes.

Experiment 1

In this first experiment, I tested whether people automatically and necessarily base predictions about others in their own knowledge. Participants either answered trivia questions before or after estimating others’ knowledge. Across the static and the anchoring-and-adjustment views, the sequence of steps required to estimate what others know should not affect judgments. Static views suggest that estimates are based upon knowledge of the content and others, which does not change with judgment conditions; anchoring-and-adjustment views suggest that all participants must anchor in their own knowledge first, regardless of the judgment conditions. However, according to the cue-utilization view, answering a question first should provide participants with mnemonic cues about their own knowledge (e.g., their own ability to answer the question and fluency with answering) which are not automatically available for those who are not first required to answer each question. People use their fluency retrieving an answer to predict their own (e.g., Benjamin, Bjork, & Schwartz, 1998) and others’ (e.g., Thomas & Jacoby, 2013) knowledge across a variety of metacognitive paradigms. If cue-utilization views are correct, requiring participants to answer questions before estimating others’ knowledge should increase the relationship between their estimates of others’ knowledge and their own ability and fluency to answer the questions.

Method

Participants

A power analysis using the G*Power computer program (Faul, Erdfelder, Lang, & Buchner, 2007) indicated that a total sample of 128 participants would be needed to detect medium-sized effects (d = 0.50) using a between-subjects t test with alpha at 0.05 and power of 0.80. One hundred and-twenty-eight participants participated through Amazon Mechanical Turk for $1.50 compensation. Basic demographic questions about age, gender, and education level were posed before the experiment began.Footnote 1 The mean age of participants who responded was 35.7 (SD = 10.20), 55% were male, all had completed high school, and 53% reported attending 4 or more years of college.

Materials

Forty trivia questions were selected from Nelson and Narens’ (1980) 300 general knowledge questions. Questions were selected to encompass a variety of different topics, including geography, entertainment, sports, science, and history.

Procedure

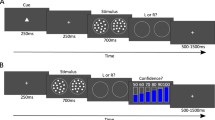
Participants were randomly assigned to the answer-before and answer-after conditions. Both groups were told “In this experiment, you will judge the percentage of other participants that will know each answer to a series of trivia questions. You will enter a percentage between 0 and 100. If you think NO ONE will know it, you can enter 0. If you think everyone will know it, you can enter 100. If you think half of the other subjects will know an answer, you should enter 50. Again, you will estimate the percentage of others that will know each trivia question.” During each trial, participants were shown a question and were given the prompt, “What percentage of other participants will know the answer?” In the answer-before condition, each participant first answered the question on their own without corrective feedback and subsequently provided their estimate of what percentage of other participants would know the correct answer. In the answer-after condition, participants first estimated others’ knowledge for all 40 trivia questions. After rating all of the trivia questions, the participants went through the entire list of questions again and provided their best answer to each question.

Results

In this and the subsequent experiment, participants’ responses were considered correct only if they matched the target exactly (although I repeated all analyses after accepting misspelled answers as correct, and all analyses were confirmed). Difficulty was calculated by the percentage of correct answers from participants across both conditions. The questions ranged in difficulty from 15% correct to 95% correct (SD = 23%), with a mean of 57%.Footnote 2 Participants in the answer-before condition performed similarly (M = .60, SD = .17) to those in the answer-after condition (M = .55, SD = .20), t(126) = 1.49, p = .14, d = 0.27.

Bases for judgments

The relationship between participants’ answers and estimates of others’ knowledge is displayed in Fig. 1. I examined the relationship between the time needed to answer each question and the prediction for others. Gamma correlations were used in most analyses because gamma correlations require no assumptions about the underlying interval nature of the scales. The intraindividual gamma correlations between time to answer and predictions for others in both conditions were negative, indicating that participants provided lower estimates for questions that required longer to answer. Participants in the answer-before condition showed a significantly stronger correlation between answer time and predictions than participants in the answer-after condition, t(126) = 4.12, p < .001, d = 0.76.

Fig. 1
figure 1

Gamma correlations between predictions of others’ knowledge and the time needed for the judge to answer the question (left side) and the accuracy of the judge’s answer (right side) in Experiment 1. Greater magnitudes indicate a stronger relationship between the judge’s processes and their estimates of others’ knowledge. Error bars show one standard error of the mean above and below the sample mean

Full size image

I also calculated the intraindividual gamma correlations between predictions for others and a participant’s own correctness. Across both conditions, correlations between a subject’s accuracy and his predictions of others’ knowledge were positive, indicating that participants gave higher predictions for others to questions they correctly answered than to questions they incorrectly answered. Participants in the answer-before condition showed a significantly larger correlation between own-correctness and predictions than participants in the answer-after condition, t(126) = 3.24, p = .002, Cohen’s d = 0.60.

Accuracy of judgments

Finally, I examined whether the changes in the bases of judgments for others across conditions translated into differences in predictive accuracy. The answer-before group gave similar overall estimates of the percent of others who could answer the questions (M = 49%, SD = 13%) than the answer-after group (M = 47%, SD = 12%), t(126) = 1.31, p = .19, d = 0.16. I computed the intraindividual Pearson correlation between estimates of others’ knowledge and the group’s overall performance on each question. Pearson correlations were calculated here because both scales (estimates on the 0–100 scale and proportion of others who knew the answer) are assumed to be interval scales. Both the answer-before condition and the answer-after condition showed greater predictive accuracy than chance (Manswer-before = 0.65, SD = 0.15), t(63) = 35.73, p < .001, d = 4.3; (Manswer-after = 0.57, SD = 0.19), t(63) = 24.35, p < .001, d = 3.0. Further, participants in the answer-before condition showed greater relative accuracy than the answer-after condition, t(126) = 2.70, p = .006, d = 0.47.

Discussion

Judgment conditions affected how strongly participants based their predictions about others in their own knowledge. Whereas estimates about others were related to participants’ processing in both conditions, participants’ predictions of others’ knowledge were more strongly tied to their own processing (i.e., response fluency and own accuracy) when they were required to answer the trivia questions before estimating others’ knowledge. Consequently, predictions were differentially accurate across conditions, such that answering the questions first prompted more accurate estimates of others’ knowledge. The results from Experiment 1 extend existing research about judging others’ memories by revealing differential use of one’s own knowledge when estimating others’ knowledge. Prior research shows that learners consider information about their own memories when predicting others’ memories (Serra & Ariel, 2014). Here, the data show that how much they consider their own processes depends upon the judgment conditions.

Estimates differed across judgment conditions, which is evidence against the strong view of knowledge estimation as content knowledge because varying judgment conditions should not change how much static knowledge participants have about others. Further, this research challenges the anchoring-and-adjustment view of knowledge estimation, as groups differ in how strongly they anchor in their own processes without any a priori predicted difference in adjustment processes. If both groups anchor in their own knowledge and there are no expected differences in the effortful adjustment process, estimates of what others know should not differ between conditions. The anchoring-and-adjustment view could be modified by suggesting that requiring participants to answer questions first causes their own cognitive processes to be more salient and compels judges to be less willing to adjust away from them.

Prior research has argued that participants automatically base their predictions of others’ knowledge in their own knowledge, unless prevented from doing so (Kelley & Jacoby, 1996; Thomas & Jacoby, 2013). Here, I argue that the reliance on one’s own knowledge as an anchor depends upon whether participants were required to answer the questions first. Attempting to answer a question can provide mnemonic cues about one’s knowledge; participants are unlikely to accurately assess what they know unless they attempt to answer test questions. This theory is bolstered by the time participants needed to provide answers and estimates. In the answer-first condition, participants needed 11.63 s (SD = 7.2) to answer the question and an additional 2.66 s (SD = 1.1) to provide their estimates of what others know. In the answer-after condition, participants provided their estimates of what others know in only 6.10 s (SD = 2.74), which is less than participants needed to answer the question.

Experiment 2

In the second experiment, I extended and replicated the results of Experiment 1 by testing estimates of others’ knowledge under a broader set of judgment conditions. Here, participants made judgments about others under two fully crossed conditions: (1) they either did or did not answer each question first (as in Experiment 1), and (2) they either did or did not receive feedback about the correct answer to each question. I compared the bases and predictive accuracy of judgments for others under these four conditions. The cue-utilization framework suggests that requiring participants to answer trivia questions will provide greater access to mnemonic cues and more strongly tie their estimates of others’ knowledge to their own processes (i.e., increased reliance on the time it takes judges to answer and judges’ accuracy) and improve the accuracy of their judgments. Further, feedback about the correct answers should provide additional metacognitive cues about the intrinsic difficulty of trivia questions, including the familiarity of the target (Leibert & Nelson, 1998) and the relationship of the cue with the target (Koriat, 1997). These additional intrinsic, diagnostic cues should reduce reliance on one’s own answering processes when estimating others’ knowledge and increase the accuracy of one’s predictions. In other words, according to the cue-utilization framework, the no-answer-required, no-feedback-provided condition should show the worst accuracy at estimating what others will know because it affords access to the fewest metacognitive cues; alternatively, the answer-required, feedback-provided condition should be the most accurate at estimating what others know because it affords access to metacognitive cues about one’s own retrieval processes (i.e., answer fluency and answer accuracy) and about the target.

Method

Participants

Prior studies have suggested that providing an answer to judges improves their accuracy with a medium effect size (Thomas & Jacoby, 2013). A power analysis using the G*Power computer program (Faul et al., 2007) indicated that a total sample of 128 participants would be needed to detect medium-sized main and interaction effects (effect size F = 0.25) using an ANOVA with an alpha at 0.05 with power of 0.80. Two hundred twenty-eight psychology students at Indiana University participated in exchange for partial course credit. One hundred students answered only the trivia questions in order to independently assess others’ knowledge of the trivia questions. The remaining 128 students were alternatively assigned to four conditions (each with 32 participants) in which they predicted the knowledge of their classmates. Of those in the experimental conditions, 56 were female and 71 were male. The mean age was 19.59 years old (SD = 1.34); 72 were freshman, 33 were sophomores, 13 were juniors, and nine were seniors.

Materials

Eighty trivia questions were selected from Nelson and Narens’ (1980) 300 general knowledge questions. Questions were selected to encompass a variety of different topics, including geography, entertainment, sports, science, and history. The normative difficulty of each question was the proportion of the 100 participants who correctly answered each question; these participants did not participate in the experimental conditions. The questions ranged in difficulty from 0% to 89% correct, with a mean percentage correct of 32% (SD = 24%).Footnote 3

Design

The experiment utilized a 2 (answer requirement) × 2 (presence of feedback) between-subjects design. Participants were or were not required to provide an answer to each question; participants were or were not given feedback about the correct answer.

Procedure

Participants completed the experiment, which was programmed with MATLAB using the Psychophysics Toolbox (Brainard, 1997) and CogSci Toolbox (Fraundorf et al., 2014) extensions on personal computers in individual testing booths. Participants were randomly assigned to the four different conditions. Participants in the answer-required conditions were told that they would answer a series of trivia questions. Then, they were told that they would “judge how well your peers or classmates would be able to answer the same questions. You will rate how likely your classmates would know these facts on a scale of 1 to 4. Please use all of the ratings (1, 2, 3, AND 4). 1 means that a different learner WILL NOT know the answer, 2 means that the new learner PROBABLY WILL NOT know the answer, 3 means that the new learner PROBABLY WILL know the answer, and 4 means that the new learner DEFINITELY WILL know the answer.” The restricted range of the scale used here reduces the noise when participants make judgments (see Benjamin, Tullis, & Lee, 2013), and should provide clean measures of judges’ ability to estimate what others know. Participants who were in the no-answer-required conditions received the same instructions, but were not told that they would answer the trivia questions first.

Trivia questions were presented one-at-a-time in a random order on the screen. Participants in the answer-required, feedback-provided condition had to first type in an answer for the question. The correct answer was then provided, and participants finally rated the others’ knowledge on a scale of 1 to 4. Participants in the answer-required, no-feedback-provided condition first answered the question and then rated others’ knowledge of it without receiving feedback about the correct answer. Participants in the no-answer-required, feedback-provided condition saw the question and answer presented simultaneously on screen and rated others’ knowledge. Finally, participants in the no-answer-required, no-feedback-provided condition saw only the question and rated others’ knowledge of the question for others without explicitly answering it or receiving feedback about the correct answer.

Results

Forty questions overlapped between Experiments 1 and 2, so we compared performance across experiments on that subset of items. There was a high correlation between the difficulty of the questions common to Experiments 1 and 2 (r = .92), although the Mechanical Turk participants in Experiment 1 performed better on the questions (M = 0.57, SD = 0.23) than the introductory psychology students here (M = 0.41, SD = 0.28); t(39) = 9.11, p < 0.001, d = 1.46. It is unlikely that the MTurk participants in Experiment 1 looked answers up while completing the experiment because the MTurk participants required similar amounts of time to answer the trivia questions (M = 11.63 s per question, SD = 7.21) as the lab participants (M = 12.14 s per question, SD = 3.87), t(126Footnote 4) = 0.49, p = 0.62, d = 0.09.

Bases for judgments

I first examined the bases of judgments of others’ knowledge (i.e., the time needed to answer the question and the participant’s correctness) for the participants who had to answer each question. The relationship between time needed to answer the trivia question and the prediction for others based upon whether feedback was provided is shown on the left side of Fig. 2. Gamma correlations between participants’ predictions for others and their own time taken to answer the question were negative across both answer-required conditions, indicating that the longer it took the participants to answer the question, the lower the predictions for others they provided. The correlations did not significantly differ depending on the presence of feedback, t(62) = 1.48, p = .14, d = 0.38.

Fig. 2
figure 2

Gamma correlations between predictions of others’ knowledge and the time needed for the judge to answer the question (left side) and the accuracy of the judge’s answer (right side) in Experiment 2. Error bars show one standard error of the mean above and below the sample mean

Full size image

The relationship between a participants’ correctness and predictions of others’ knowledge is shown on the right side of Fig. 2. Gamma correlations between participants’ accuracy and their predictions of others’ knowledge were positive across both answer-required conditions, indicating that participants gave higher predictions for others to questions they correctly answered than to questions they incorrectly answered. The correlation was significantly stronger when participants received feedback than when they did not receive feedback, t(62) = 2.65, p = 0.01, Cohen’s d = 0.68.

Accuracy of judgments

Gamma correlationsFootnote 5 were calculated between predictions for others and the normative difficulty of the individual trivia questions to assess the relative accuracy at predicting others’ knowledge, and they are displayed in Fig. 3. All gamma correlations were significantly greater than zero, indicating that estimates were more accurate than chance (ps < .001). A 2 (answer requirement) × 2 (presence of feedback) ANOVA on the gamma correlations revealed a main effect of answer required, F(1, 124) = 9.70, p = .002, ηp2 = 0.07, such that requiring an answer produced more accurate predictions for others, and a significant main effect of feedback, F(1, 124) = 21.10, p < .001, ηp2 = 0.15, such that providing feedback increased accuracy of predictions for others, but no interaction, F(1, 124) = 0.05, p = .83, ηp2 < 0.001.

Fig. 3
figure 3

Gamma correlations between difficulty and predictions of others’ knowledge in Experiment 2 conditionalized upon answer requirement and presence of feedback. Higher gamma correlations show greater resolution or accuracy in predictions. Error bars show one standard error of the mean above and below the sample mean

Full size image

Discussion

The conditions under which predictions for others are elicited changed both the cues upon which people based their judgments of others and their relative accuracy. When feedback was provided, predictions for others were more strongly related to the judge’s own accuracy. Further, judgment conditions changed the accuracy of estimates: judges’ predictions of others’ knowledge were more accurate when they had to answer the questions themselves and when they were provided the correct answer.

Requiring participants to answer trivia questions changed how they estimated others’ knowledge and the accuracy of their estimates. The results of Experiment 2 align with predictions of the cue-utilization view of knowledge estimation. Reliance on one’s own perspective was modulated by the kind and diagnosticity of cues present. When participants were asked to answer the questions first without correct feedback, they relied heavily on how long it took them to answer the question; the addition of corrective feedback increased their consideration of whether their answer was correct (a diagnostic cue).

Providing participants with the correct answer did not interact with requiring participants to answer the questions. The independence of these two factors suggests that the presence of the correct answer has a separate and distinct effect from interfering with participants’ own ability to access their knowledge. The knowledge estimation as cue-utilization framework suggests that the two processes provide independent cues related to the difficulty of the trivia questions. Requiring an answer elicits cues related to one’s own ability to answer the question (i.e., mnemonic cues), whereas providing the correct answer showcases metacognitive cues related specifically with that answer (i.e., intrinsic cues like answer familiarity).

Experiment 2 showed that basing judgments of others on one’s own experiences can increase the predictive accuracy of judgments about others’ knowledge—which is an additional contribution of this research. Nickerson (1999) suggests little attention has been given to the possibility of improving the accuracy with which people estimate what others know.

Simply by requiring participants to answer the trivia questions before estimating others’ knowledge, participants’ estimates have improved. Participants’ attempts to answer provided diagnostic cues about the difficulty of the material that were not accessed when retrieval attempts were not made (in the no-answer-required conditions). In Experiment 3, I explored whether one’s own experiences can mislead people’s predictions about others and produce less accurate judgments of others’ knowledge.

Experiment 3

According to the knowledge estimation as the cue-utilization framework, participants should adeptly weight their own experiences based upon their perceived diagnosticity; when one’s own experiences do not represent others’ experiences, participants should weight them lightly. In Experiment 3, I examined whether judgment conditions changed if participants could disregard their own experiences when their own experiences proved to be nondiagnostic of the correct answers. To do so, I included questions that often elicit incorrect answers. When corrective feedback is provided, one’s own experiences at retrieving incorrect answers may become nondiagnostic to predict others’ knowledge. Therefore, participants should weight their own experiences answering the questions (i.e., time needed to answer) only weakly in these circumstances. Alternatively, when one’s own knowledge is inaccurate and no feedback is provided, access to one’s own knowledge may mislead predictions about others’ knowledge and greater reliance on one’s own idiosyncratic experiences could hamper accuracy at predicting others’ knowledge. Specifically, predictions from the cue-utilization framework suggest that requiring answers for misconception questions without providing feedback will produce the least accurate estimates of what others know because participants will base judgments on misleading cues (e.g., the time needed to produce an incorrect answer). Consequently, unlike prior experiments, the no-answer-required, no-feedback-provided condition may be more accurate than the answer-required, no-feedback-provided condition.

Method

Participants

Data from 128 participants were collected through Amazon Mechanical Turk for $1.50 compensation, in order to detect medium-sized effects (effect size F = 0.25) using an ANOVA with an alpha at 0.05 with power of 0.80. Eighty participants identified as male, 47 as female, and one did not report their gender. The average age was 33.47 years (SD = 9.49).

Materials

A list of 40 trivia questions was compiled. Twenty “regular” questions were selected from the 80 used in Experiment 2 and included a wide range of difficulties and topics. Participants in Experiment 2 answered this subset of questions 41% correctly (SD = 30%), with a range from 2% to 95%. Additionally, I created 30 misconception questions that would potentially elicit a common wrong answer consistently. I gathered the question ideas from various Internet sources when I searched for “common misconceptions.” I narrowed the 30 questions down to 20 based upon the misconceptions that were elicited during pretesting with a small group of graduate students. An example of a misconception question is: What restaurant has the most stores in the world? Misconception answer: McDonald’s; correct answer: Subway. Misconception questions were selected when less than 25% of students produced the correct answer and more than 25% of students provided the same incorrect answer. As in Experiment 1, participants answered 40 trivia questions. Questions are shown in the Appendix 1.

Design

The experiment utilized a 2 (answer required or not) × 2 (feedback provided or not) × 2 (regular or misconception question) mixed-subjects design. Participants were or were not required to provide an answer to each question; participants were or were not told what the correct answer was; and all participants answered regular and misconception questions. Judges used a 0–100 scale to estimate others’ knowledge, as in Experiment 1. Increasing the range of the scale may introduce more noise into the judgment process (see Benjamin, Tullis, & Lee, 2013) but may map more naturally on to the process of estimating what others know. Further, the 0–100 scale allowed me to assess calibration (or absolute accuracy—a measure of the degree to which the judges’ estimates correspond to actual difficulty), in addition to predictive resolution (or relative accuracy—a measure of the degree to which judges correctly ordered the difficulty across questions). Further, using multiple judgment scales tests the generalizability of the results from Experiment 2.

Procedure

The experiment proceeded similarly to Experiment 2. The main differences were that half of the questions were intended to be misconception questions and participants were asked, “Out of 100 other participants, how many will get this trivia question correct? Enter a number between 0 and 100.” The experiment was programmed using Collector Software. Participants were recruited through Amazon Mechanical Turk, completed the experiment online, and were paid $1.50 for their time.

Results

The difficulty of questions in this experiment was calculated by the percentage of correct answers from participants across both answer-required conditions. From the 20 questions that were common across Experiments 2 and 3, there was a high correlation between their difficulty in Experiments 2 and 3 (r = .93), although the Mechanical Turk participants in this experiment performed better on the common regular questions (M = 0.62, SD = 0.25) than the introductory psychology students in Experiment 2 (M = 0.41, SD = 0.30), t(19) = 7.95, p < .001, d = 1.82. Again, there is no evidence that MTurk participants took longer to answer the trivia questions (M = 12.85 s per question, SD = 7.69) than the lab participants (M = 11.26 s per question, SD = 2.74), t(126) = 1.55, p = .12, d = 0.28.

Accuracy of answers were examined to verify whether the misconception questions produced consensus wrong answers (more than 25% of the participants provided the same incorrect answer and less than 25% of the participants provided the correct answer). Of the 20 misconception questions compiled, only 17 met these criteria; the other three questions were answered correctly by more than 25% of the participants and had fewer than 25% of participants provide the same incorrect answer. Only the 17 questions that met the criteria were considered misconception questions in all further analyses. The three other questions that were initially thought to be misconceptions, but ended up not meeting the criteria, were grouped with the 20 “regular” questions from Experiments 1 and 2.Footnote 6

Bases for judgments

For clarity and because the questions were not randomly assigned to be “regular” or “misconception” conditions, the regular questions were analyzed separately from the misconception questions across all analyses. As in the first two experiments, I examined the relationship between the time needed to answer each question and the prediction for others. For the regular questions, the gamma correlations between time to answer and predictions for others in both conditions were significantly less than zero (ps < .001), indicating that the longer it took the participants to answer the question, the lower the predictions for others they provided. No difference was found between feedback and no-feedback conditions, t(62) = 1.58, p = .12, d = 0.37. For the misconception questions, the correlation between time to answer and predictions for others differed based upon the presence of feedback. Participants who received no feedback showed a correlation significantly less than zero, t(31) = 4.51, p < .001, d = 0.78, whereas participants who received feedback showed a numerically positive correlation that did not differ from zero, t(31) = 0.78, p = .44, d = 0.14. These correlations significantly differed, t(62) = 3.93, p < .001, d = 1.00.

The relationship between a participant’s correctness and predictions of others’ knowledge is shown in Fig. 4. For regular questions, the results replicated Experiment 2: Gamma correlations between subjects’ accuracy and their predictions of others’ knowledge were significantly greater than zero (ps < .001) across both answer-required conditions, indicating that participants gave higher predictions for others to questions they correctly answered than to questions they incorrectly answered. The correlation did not differ based upon the presence of feedback, t(62) = 1.64, p = .11, d = 0.39. For misconception questions, a different pattern arose. Participants provided with feedback still showed a correlation greater than zero, t(24) = 9.18, p < .001, d = 1.82, between their own accuracy and predictions for others, but participants with no feedback showed a correlation less than zero, t(21) = 3.49, p = .001, d = 0.73, between their own accuracy and predictions for others. These correlations differed significantly, t(45Footnote 7) = 7.46, p < .001, d = 2.36.

Fig. 4
figure 4

Gamma correlations between predictions of others’ knowledge and the time needed for the predicting subject to answer the question and the accuracy of the predicting subject’s answer in Experiment 3, conditionalized upon the presence of feedback. Left panel shows the regular questions, and the right panel shows the misconception questions. Error bars show one standard error of the mean above and below the sample mean

Full size image

Relative accuracy

To assess the relative accuracy of predictions for others, the Pearson correlation between predictions for others and difficulty for others was calculated for each subject in this experiment, as in Experiment 1. Correlations between participants’ predictions of others’ knowledge and others’ actual knowledge are displayed in Fig. 5. All correlations were significantly greater than zero (ps < .001), except for the answer-required, no-feedback misconception group (p = .13). For the regular questions, a 2 (answer required or not) × 2 (feedback provided or not) between-subjects ANOVA on correlations revealed a significant main effect of answer required, F(1, 124) = 4.45, p = .04, ηp2 = 0.04, and a significant main effect of feedback provided, F(1, 124) = 9.61, p = .002, ηp2 = 0.07, but no interaction, F(1, 124) < 0.001, p = .99, ηp2 < 0.001. As in Experiment 2, participants’ predictions were more accurate when they first answered the questions and when they received feedback.

Fig. 5
figure 5

Pearson correlations between difficulty and predictions of others’ knowledge in Experiment 3, conditionalized upon answer requirement and presence of feedback. Left panel shows the regular questions, and the right panel shows the misconception questions. Higher correlations show greater resolution or accuracy in predictions. Error bars show one standard error of the mean above and below the sample mean

Full size image

However, for the 17 misconception questions, a 2 (answer required or not) × 2 (feedback provided or not) between-subjects ANOVA on correlations revealed a significant interaction between answer required and feedback, F(1, 124) = 10.92, p = .001, ηp2 = 0.08, a main effect of feedback provided, F(1, 124) = 7.28, p = .008, ηp2 = 0.06, but no main effect of answer required, F(1, 124) = 1.64, p = .20, ηp2 = 0.01. For the misconception questions, participants’ predictive accuracy depended upon the interaction of the presence of feedback and answer requirement, such that participants were most accurate when they had to answer the question and received feedback.

Calibration

Asking participants to predict how many other participants out of 100 would correctly answer each question allowed me to calculate calibration between predictions for others and actual difficulty. Calibration was calculated by taking the absolute value of the difference between the prediction for others and the percentage of others who correctly answered each question. Calibration scores are displayed in Fig. 6. For the regular questions, a 2 (answer required or not) × 2 (feedback provided or not) between-subjects ANOVA on calibration revealed a significant main effect of feedback provided, F(1, 124) = 16.14, p < .001, ηp2 = 0.12, but no main effect of answer required, F(1, 124) = 2.87, p = 0.09, ηp2 = 0.02, or interaction, F(1, 124) = 0.06, p = .80, ηp2 = 0.001. Participants were better calibrated when they were provided feedback about the correct answer.

Fig. 6
figure 6

Calibration (the absolute value of the difference between difficulty and predictions of others’ knowledge) in Experiment 3, conditionalized upon answer requirement and presence of feedback. Left panel shows the regular questions, and the right panel shows the misconception questions. Larger values of calibration reflect worse accuracy in predictions. Error bars show one standard error of the mean above and below the sample mean

Full size image

For the 17 misconception questions, a 2 (answer required or not) × 2 (feedback provided or not) between -subjects ANOVA on calibration revealed a significant interaction between answer required and feedback, F(1, 124) = 5.14, p = .03, ηp2 = 0.04, a main effect of feedback provided, F(1, 124) = 94.98, p < 0.001, ηp2 = 0.43, but no main effect of answer required, F(1, 124) = 0.038, p = .85, ηp2 < 0.001. For the misconception questions, calibration was affected by the interaction of feedback and response requirement. If participants received feedback, predictions were better calibrated when they first answered the question. If participants did not receive feedback, predictions were better calibrated when they did not first answer the question.

Discussion

In Experiment 3, the conditions under which predictions for others were made impacted the bases upon which people made predictions and the accuracy of estimates. Participants shifted between weighting different kinds of metacognitive cues when predicting others’ knowledge, depending on the diagnosticity of the cues. For example, judgment conditions affected how much participants relied upon the time it took them to answer each question: specifically, for misconception questions, participants who were given the correct answer ignored the time it took them to answer each question when estimating others’ knowledge.

Because judgment conditions affected the kinds of cues judges used when making estimates of others’ knowledge, judgment conditions also affected the accuracy of their judgments. For standard questions, requiring an answer and providing feedback improved both the resolution (as in Experiments 1 and 2) and calibration of those judgments. For misconception questions, the consequences of querying one’s own knowledge depended upon the presence of feedback. When feedback about the correct answer was provided, querying one’s own knowledge led to more accurate resolution and calibration in predicting others’ knowledge than not querying one’s own knowledge. However, when no feedback about the correct answer was provided, querying one’s own knowledge led to numerically worse resolution and calibration in predicting others’ knowledge than not querying one’s own knowledge.

Estimates of others’ knowledge are typically tied to judges’ accuracy in answering the questions, even when judges are not provided feedback about the correctness of their answers. Basing estimates of others’ knowledge in one’s own accuracy (even when one’s own accuracy is not objectively known) may reveal a new instantiation of the consensuality principle. People may judge their confidence in an answer by monitoring its consensuality rather than its objective accuracy (Koriat, 2008; Koriat & Adiv, 2011). Just as in the consensuality principle, people may base estimates of what other people know by how quickly and consistently they reach particular answers themselves, unless more diagnostic cues about difficulty are available to consider. Basing estimates in how quickly and consistently judges answer questions can lead their estimates astray, as shown in the no-feedback-provided condition of Experiment 3, whereby estimates of others’ knowledge are higher for incorrectly answered questions than correctly answered ones.

General discussion

Across three experiments, judgment conditions affected the cues judges used to estimate others’ knowledge of trivia questions. These results mimic those found when people predict their own future performance (Nelson & Dunlosky, 1991). In order to make predictions about their own future cognitive performance, people infer their future performance from several kinds of metacognitive cues, including intrinsic stimulus characteristics, extrinsic study factors, and idiosyncratic mnemonic experiences (Koriat, 1997). The conditions under which self-predictions are made change which types of cues people can access, and, consequently, they influence the predictive accuracy of self-predictions (Benjamin et al., 1998; Nelson & Dunlosky, 1991). Similarly, when predicting others’ knowledge, the judgment conditions shift which cues are available to the judge and ultimately affect the predictive accuracy of estimates about others’ knowledge.

Competing theories

According to knowledge estimation as content knowledge, the ability to estimate the others’ knowledge is an accumulation of static knowledge; people gain information about the difficulty of material for others through interactions with others and the content (Driel et al., 1998; Magnusson et al., 1999). However, as the current experiments suggest, knowledge estimation is much more dynamic and context dependent than suggested by this theory.

Anchoring-and-adjustment theories of knowledge estimation posit that judges must initially and automatically base their estimates of others’ knowledge in their own knowledge. In fact, anchoring-and-adjustment theories suggest that perspective taking is difficult because people cannot ignore their own idiosyncratic knowledge when making judgments of others’ cognition, a general finding that has been labeled the “curse of knowledge” (Birch, 2005). Here, I have shown limits to that theory. Judgment conditions change how tightly judges’ estimates of others’ knowledge align with their knowledge, even when conditions do not afford for differential adjustment. Judges may not automatically base their estimates on their own knowledge, as judges may not even query their own knowledge before estimating others’ knowledge. Metacognitive research shows that people do not automatically know what they know; rather, people must infer their knowledge from available cues, like their ability to retrieve an answer and their retrieval fluency. When these cues are blocked by judgment conditions, judges can no longer base estimates of others in their own knowledge. Hence, these results suggest boundary conditions to the anchoring-and-adjustment view or reveal areas in which anchoring-and-adjustment theories need to be modified.

The results of these three experiments align with predictions from the cue-utilization framework. Estimating others’ knowledge seems like a result of a dynamic process of weighting a variety of salient and accessible cues. First, querying participants about their own knowledge by asking them to answer the trivia questions shifted which metacognitive cues were salient and accessible, and thereby affected the accuracy of judges’ estimates. Second, participants shifted between different cues based upon the diagnosticity of the cue. For standard questions (when their own answering processes reflected general knowledge), participants relied strongly on cues related to their own answers (e.g., the time it took to answer the question). For misconception questions with corrective feedback (when participants’ answer processes were shown to not reflect reality), participants ignored how long it took them to produce their answer when estimating others’ knowledge. Similarly, the presence of feedback when no answer is required may have shifted judges away from relying on their own experiential processes (i.e., mnemonic cues) and forced them to rely upon other types of cues, including intrinsic cues and explicit beliefs about difficulty of material (see Mueller & Dunlosky, 2017).

Prior research has shown that presenting a solution with the question changes estimates of others’ knowledge but reveals differential effects on the accuracy of those estimates. Kelley and Jacoby (1996) showed that giving judges anagram solutions simultaneously with the anagrams reduces their ability to accurately estimate the difficulty of those anagrams for others. However, as seen here, giving judges trivia answers increased their accuracy at estimating the difficulty for others. The cue-utilization framework suggests that the presence of the answer in each case changes the availability of diagnostic cues. For both trivia questions and anagrams, solutions prevent people from attempting to solve the problem on their own, and thereby reduce the influence of personal mnemonic cues related to attempted solutions (e.g., ability to solve and solution time). However, the presence of the answer may provide additional cues about the difficulty of the question. Trivia answers should provide several strongly diagnostic cues related to the target information (e.g., target familiarity, cue-to-target associative strength), but anagram solutions likely provide only weakly diagnostic cues about the difficulty of the anagram (e.g., how common the answer word is). So, whereas presenting the answer reduces mnemonic cues about anagram and trivia difficulty, the answer provides several additional new intrinsic cues about the difficulty of the trivia questions (but may not provide similar diagnostic cues related to anagrams). The importance of knowing the correct answer for estimating the difficulty of trivia questions is showcased by the very large effect of feedback across Experiments 2 and 3, as compared with the much smaller effect of requiring people to answer the questions themselves. Judgment conditions can shift which cues are available (and how much those cues are weighted), as suggested by the isomechanism framework of metacognitive judgments, which suggests that all metacognitive judgments are inferred from available, salient, and relevant cues (Dunlosky & Tauber, 2014). The cue-utilization framework, then, may be an instantiation of the isomechanism framework.

Judges may be able to switch between the different knowledge estimation frameworks when making metacognitive judgments about others. The different accounts may be able to best explain different situations and patterns of data. In fact, recent research has shown that perspective taking is domain specific (Ryskin, Benjamin, Tullis, & Brown-Schmidt, 2015). How perspective taking functions in language production may be entirely different than how perspective taking functions in knowledge estimation. Communicating about different visual perspectives may be a different process than predicting what someone else knows because visual perspectives are physically present to the interacting agents; in contrast, one’s own ability to answer trivia questions is not automatically apparent and accessible. One’s own knowledge must be inferred from a variety of differentially diagnostic cues. The cue-utilization framework may subsume the static knowledge and anchoring-and-adjustment accounts, as explicit knowledge of others (as in the static knowledge view) and one’s own cognitive processes (as in the anchoring-and-adjustment account) can both be kinds of cues judges may rely upon when estimating what others know. How we estimate a specific other person’s knowledge remains unexamined. In language production, past experiences with or knowledge about a specific person can shift the uttered message (see Fussell & Krauss, 1992, for examples). How we utilize cues about a specific person’s knowledge and whether they override more general cues in knowledge estimation are open questions.

Social metacognitive monitoring and control

Accurate monitoring of one’s own learning is vital to effective self-regulation. Metacognitive monitoring guides how one chooses to study (Metcalfe & Finn, 2008; Nelson & Narens, 1990; Thiede & Dunlosky, 1999; Tullis & Benjamin, 2012a), and how one chooses to study greatly impacts learning. Precise monitoring of one’s own learning can lead to judicious study choices and ultimately effective learning and test performance (Thiede, Anderson, & Therriault, 2003; Tullis & Benjamin, 2011). Errors or biases in one’s own monitoring can lead to deficient use of control during study and inefficient or ineffective learning (Atkinson, 1972; Karpicke, 2009; Tullis & Benjamin, 2012b). Similarly, accurate monitoring of others’ knowledge likely leads to effective control of others’ study. The cue-utilization framework for predicting others’ knowledge may ultimately suggest methods and conditions to promote accurate monitoring and control of others’ knowledge.