Introduction

The ability to reflect on our thoughts and decisions is a key facet of human cognition. The term metacognition encompasses a range of such reflective processes, including the ability to estimate confidence in our decisions (Fleming, Dolan, & Frith, 2012; Nelson & Narens, 1990; Yeung & Summerfield, 2012). To illustrate, a scaly tail protruding from under a bush while hiking could be identified as belonging to either a snake or a lizard, but a sense of confidence in this decision will also be important for behaviour – a decision that the tail belongs to a lizard might suggest that the individual can proceed without altering their path, but a low sense of confidence in this decision might instead trigger more cautious behaviour. Confidence, however, is not always well aligned with the accuracy of perceptual decisions (Fleming & Lau, 2014; Mamassian, 2016; Nelson & Narens, 1990) – an identification of lizard might be associated with a high degree of confidence, but this could well be a dangerous error.

Reports of dissociations between perceptual performance and confidence are prevalent in the literature (Fetsch, Kiani, Newsome, & Shadlen, 2014; Kiani, Corthell, & Shadlen, 2014; Lau & Passingham, 2006; Rahnev, Maniscalco, Luber, Lau, & Lisanby, 2012; Rounis, Maniscalco, Rothwell, Passingham, & Lau, 2010; Spence et al., 2016; Spence, Mattingley, & Dux, 2018; Zylberberg, Fetsch, & Shadlen, 2016; Zylberberg, Roelfsema, & Sigman, 2014). For example, Spence, Dux, and Arnold (2016) showed that manipulating the range of direction signals within a dot motion stimulus had a robust effect on confidence, despite controlling for changes in perceptual sensitivity (see also Allen et al., 2016). In one of Spence and colleagues’ experiments, two clouds of moving dots appeared one after the other, and participants completed a decision-making task in which they judged whether the average direction of the second cloud of dots was clockwise or anticlockwise compared with the first cloud of dots. The variability of this sensory information was manipulated by varying the range of motion direction across the population of dots – in other words, whether the dots moved relatively consistently around the mean direction, or more erratically. Despite holding perceptual performance constant, greater signal range was associated with lower confidence ratings. This suggests that participants tended to overemphasize signal variability when estimating their confidence in their decisions, showing this variable to be a powerful heuristic for confidence judgements.

Interestingly, research has shown that confidence is even sensitive to factors that are irrelevant for the first-order perceptual decision. For example, response time to make an initial perceptual decision should not causally influence the decision itself, occurring after the decision has been made, but has nevertheless been shown to contribute to retrospective estimation of confidence – an inverse relationship is typically observed, with higher confidence ratings generally following fast responses (Vickers & Packer, 1982). This effect holds even when response times are inflated artificially (Kiani et al., 2014). In addition, extending their earlier work, Spence, Mattingley, and Dux (2018) showed that sensory variability can bias confidence even when it relates to a stimulus dimension that is irrelevant for the perceptual decision. Spence and colleagues introduced an additional brightness manipulation to their task that was orthogonal to the direction range manipulation of their earlier study. Participants were post-cued on each trial to make a comparison judgement as to either the relative motion direction or the relative brightness of the two stimuli. Their results showed that greater variability of direction of motion signals was once again associated with lower confidence ratings, even for trials in which the perceptual decision and confidence estimation related to brightness judgements.

In everyday behaviour, visual discrimination and the accompanying sense of confidence rarely concern highly controlled visual objects such as grating stimuli, which are typically used under experimental conditions. Thus far, it is not known whether the influence of confidence heuristics persists over time, and which factors might promote or attenuate reliance on such heuristics. Recently, Carpenter et al. (2019) conducted a study investigating whether metacognitive ability can be enhanced through training, showing that the quality of metacognitive evaluations improved following training when feedback was tailored specifically to metacognitive performance, rather than visual discrimination performance. Their work demonstrates flexibility of metacognitive ability over time, but did not address the factors that might drive this improvement. Confidence heuristics are one such candidate, in that they have been shown to lead to suboptimal metacognitive evaluations. Reducing reliance on these suboptimal decision strategies might therefore be one mechanism through which metacognitive ability improves through training.

Here we present a preregistered study that investigated whether the susceptibility of confidence estimation to such decision heuristics can be reduced through training. The experimental task was based on Spence, Mattingley, and Dux (2018; Experiment 3): Before and after training, participants made comparison judgements of the direction of motion of random dot kinematogram stimuli, in which the range of direction signals within each stimulus was manipulated across trials. Our first aim was to determine whether the extent to which signal range affects confidence estimation would be attenuated through training. In parallel, we evaluated whether the relationship between response time and confidence was reduced through training.

Next, we were interested in factors that contributed to the effectiveness of training. We specified a non-directional hypothesis regarding group differences in the response to training, comparing training effects in an experimental group who trained on stimuli with varying levels of signal range with a second experimental group who trained on stimuli with a fixed level of signal range. On the one hand, participants exposed to variable signal range during training may benefit from practicing the task in a more unpredictable environment, and, consequently, may become less influenced by this variability. On the other hand, participants exposed to a fixed level of signal range must develop an alternative strategy for confidence estimation that does not draw on signal range as a heuristic for confidence (because it is not available to them during training). If they persist with such a strategy at the post-training session, their confidence estimation may be tolerant to re-introduction of signal variability. In the visual search literature, for instance, Leber and Egeth (2006) demonstrated that attentional capture could be mitigated depending on the task that participants had completed previously, attributing their results to persistence of distinct search strategies.

We also addressed the question of whether feedback during training was necessary to attenuate the effect of signal range on confidence ratings. To test the role of feedback, we evaluated training effects in an experimental group who trained on stimuli with varying levels of signal range, but who did not receive trial-by-trial accuracy feedback during their training sessions. We chose to focus on varying levels of signal range during training in this group, as this was most similar to the task that participants completed during pre- and post-training.

A final aim of the study was to determine whether any training effects on confidence estimation were accompanied by improvements in insight into the quality of confidence decisions. Whereas metacognitive bias refers to the degree to which an observer is under- or over-confident in their decisions, metacognitive sensitivity refers to the degree to which an observer can discriminate between their own correct and incorrect decisions (Fleming & Lau, 2014). Extending on this, Maniscalco and Lau (2012) proposed an informative metric of metacognitive efficiency, meta-d’, which is independent of bias, and independent of the overall level of accuracy on the task. To investigate whether training improves metacognitive efficiency, as indexed by meta-d’, we tested a directional hypothesis that if training improves the quality of confidence judgements, meta-d’ should increase from pre- to post-training.

Materials and methods

Experimental design and research plan

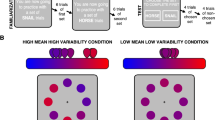
To evaluate the effect of training on confidence judgements following perceptual decisions, we used a pre-post design with three training sessions (five sessions completed on separate days), during which participants practiced a perceptual decision-making task in combination with confidence judgements. Our primary measures were confidence ratings and accuracy of perceptual decisions. We used a perceptual decision-making task based on Spence, Mattingley, and Dux (2018), which required participants to compare the average direction of motion of two successively presented clouds of moving dots (Fig. 1A). In this task, the range of motion direction signals within the dot clouds was manipulated across four levels (±5°, 10°, 20°, 30° from mean direction; Fig. 1B). We initially preregistered a study plan with two experimental groups, which differed according to whether they were exposed to variable signal range or a fixed level of signal range during their training sessions. Based on the analysis of the data from these participants, we preregistered an additional experimental group to investigate the role of feedback during training.

Fig. 1
figure 1

(A) Behavioural paradigm. Participants viewed two successive dot motion stimuli, and made a perceptual decision as to whether the mean direction of motion of the second stimulus was clockwise or anti-clockwise compared with the first stimulus. Participants then rated their confidence in their perceptual decision. (B) Direction Signal Range manipulation. The range of motion direction signals around the mean was manipulated across four levels (±5°, 10°, 20°, and 30°). (C) Training protocol and experimental groups. In the pre- and post-training sessions, all participants completed 490 trials of the decision-making task, in which signal range varied across trials over four levels, and made a confidence rating following each decision. No performance feedback was given. During the three training sessions, participants completed 410 trials of the decision-making task according to the training protocol corresponding to their experimental group. The training protocol differed in whether participants practiced perceptual decisions for motion stimuli that varied across trials over the four signal range levels, or whether they practiced a single, fixed signal range level during their training sessions, and whether, after providing their confidence rating, they were informed whether their initial perceptual decision had been correct or incorrect

Full size image

The groups differed only in the format of their training sessions (Fig. 1C). Participants in the Variable Range + Feedback group practiced perceptual judgements for stimuli with variable signal range, across the four signal range levels, randomly intermixed across trials, and received trial-by-trial accuracy feedback. Participants in the Fixed Range + Feedback group practiced perceptual judgements for stimuli with a fixed signal range, whereby each participant was pseudo-randomly assigned one of the four signal range levels to practice during their training sessions; participants in this group also received trial-by-trial accuracy feedback during training. Participants in the Variable Range No Feedback group received identical training to participants in the first group, except that they did not receive feedback on their performance. Participants in the first wave of data collection were randomly allocated to the first two groups (ensuring equal numbers in each). Participants in the third experimental group were tested in a subsequent wave of data collection.

The study plan specified that data were to be collected under a Bayesian sampling plan, to test until we achieved a Bayes Factor BF10 > 3 or BF10 < 0.333 (evidence for the alternate hypothesis over the null, and for the null over the alternate, respectively) on the three-way interaction between Signal Range (±5°, 10°, 20°, 30°), Session (Pre-training, Post-training), and Group (Variable Range + Feedback, Fixed Range + Feedback) on Confidence Ratings. We also included a minimum sample size of 12 participants per group, and a maximum sample size of 40 participants per group. This stopping rule applied to data collection for the first two experimental groups only; following this, we collected data until the number of participants in the third group was matched to the other two groups. Our full design included a repeated-measures factor of Session (Pre-training, Post-training), a repeated-measures factor of Signal Range (i.e., range of direction signals in the moving dot stimulus; ±5°, 10°, 20°, 30°), and a between-groups factor of Group (Variable Range + Feedback, Fixed Range + Feedback, Variable Range No Feedback).

Participants

Participants aged 18–35 years were recruited for the study from The University of Queensland community via online advertisements. Participants were not eligible to participate if they did not have normal or corrected-to-normal vision, or if they were not neurologically healthy. Adhering to the Bayesian sampling plan described above, we initially collected data from 54 participants in the first two experimental groups. Of these, two participants were excluded because the incorrect experiment script was run, two participants were excluded because they did not complete all of the experimental sessions, and one participant was excluded because their behavioural performance was at chance. We evaluated the three-way interaction between Signal Range (±5°, 10°, 20°, 30°), Session (Pre-training, Post-training), and Group (Variable Range + Feedback, Fixed Range + Feedback) on Confidence Ratings as follows: we first calculated the Range effect at Pre- and Post-training, separately for the two experimental groups, as the difference between Confidence ratings for the 5° and 30° Range conditions (the groups that differed most in variability). We then calculated the change in Range effect from Pre- to Post training for the two groups, and compared these with a Bayesian independent groups t-test. This test yielded a BF10 of 0.309, indicating no group differences in the change in Range effect from Pre- to Post-training, and thus meeting our stopping criteria. Based on the analysis of the data from these participants, we preregistered a third experimental group (Variable Range No Feedback), and collected data from 25 new participants, to evaluate the role of feedback in training effects on confidence. Data from one participant were excluded because not all of the sessions were completed. The final sample consisted of 73 participants (25 in Variable Range + Feedback group; 24 in Fixed Range + Feedback group; 24 in Variable Range No Feedback group). The composition of the experimental groups was similar for sex (five males in Variable Range + Feedback group, nine males in Fixed Range + Feedback group, and seven males in Variable Range No Feedback group), mean age (25.1 years in Variable Range + Feedback group, 22.3 years in Fixed Range + Feedback group, and 24.9 years in Variable Range No Feedback group), and self-reported handedness (20 right-handed in Variable Range + Feedback group, 23 right-handed in Fixed Range + Feedback group, and 21 right-handed in Variable Range No Feedback group). Participants provided informed written consent and were reimbursed at a rate of $20 per hour of participation ($80 total, for five sessions). The study was approved by the Human Research Ethics Committee at The University of Queensland.

Stimuli

Experimental stimuli were random dot kinematograms composed of 100 white dots presented against a black background. Each dot moved at a speed of 80 pixels per second, with a random component of two pixels. Dots were presented within a circular field centred on fixation, with a diameter of 6.5° of visual angle. Each individual dot measured 1 pixel in diameter. The dots within each stimulus moved with 75% coherence around a mean angle of direction. The range of motion direction within each stimulus was manipulated across four levels (±5°, 10°, 20°, 30°; Fig. 1B). Stimuli therefore varied in the consistency of the direction of motion of the dots. The stimulus screen also contained three red centre dots presented along the vertical meridian.

On each trial, two stimuli were presented successively. Stimuli within a trial were always drawn according to the same Signal Range condition, but the mean direction of motion differed between them. The direction of motion of the first stimulus was drawn from a gaussian distribution with a standard deviation of 5 and was randomly chosen on each trial to be either leftward or rightward of the vertical meridian. In addition, trials alternated as to whether the direction of motion was upwards or downwards, to minimise motion after-effects. The angular difference of mean motion direction between the two stimuli was controlled via a QUEST procedure (prior threshold estimate: 20°, prior threshold standard deviation estimate: 10°), implemented independently in each session, to maintain perceptual performance at 75% accuracy. Three identical QUEST staircases were implemented, randomly interleaved across trials. The angular difference on each trial was selected as 10 ^ QuestQuantile, or the maximum specified angular difference of 33°, whichever was smaller. We chose to maintain performance at 75% accuracy, to investigate confidence independently of performance, and to ensure that the task did not get too easy with extended practice (within and across sessions).

Procedure

The experiment was presented on a 24-in. Asus LED monitor via a Mac Mini running MATLAB and the Psychophysics Toolbox 3 (Brainard, 1997; Kleiner et al., 2007), at a viewing distance of approximately 57 cm. Each trial began with a fixation screen for 700 ms, followed by the first dot motion stimulus for 500 ms, a fixation interval for 750 ms, the second dot motion stimulus for 500 ms, and a fixation interval for 200 ms prior to a response prompt. On each trial, participants responded whether the average direction of motion of the second stimulus was clockwise or anticlockwise relative to the first, by pressing the ‘.’ or ‘/’ key on the keyboard. Participants were able to make their response following the offset of the second stimulus. Response time was recorded as the time from stimulus offset to the time of the button press. Following the perceptual response, participants made a confidence rating on a 1–4 scale, using the ‘z’, ‘x’, ‘c’ or ‘v’ keys on the keyboard. Participants were instructed to remain fixated during each trial.

Participants attended five sessions at The University of Queensland (Fig. 1C). Sessions were completed on separate days, within a maximum period of 2 weeks, with each session lasting approximately 45 min. During the first session, participants provided informed consent, were given instructions, and completed 16 practice trials with performance feedback, before completing the experimental trials. Participants completed 490 experimental trials in Sessions 1 and 5 (Pre- and Post-training), and did not receive feedback on their performance. During sessions 2, 3 and 4 (training sessions), participants completed 410 trials. During the training sessions, participants in the Variable Range + Feedback and Fixed Range + Feedback groups received trial-by-trial accuracy feedback concerning their perceptual decision, after giving their confidence rating; participants in the Variable Range No Feedback condition did not receive any feedback. Participants were given the opportunity to take a short break after every 100 trials. The first ten experimental trials in each session were dummy trials and were dropped from analysis for each session, allowing the participant to settle into the task. The Quest staircases were introduced following the dummy trials. Each cell of the design (i.e., each Signal Range level at Pre- and Post-training) included 120 trials per participant. Trial order was randomized within each session.

Results

Behavioural data were collated and analysed using MATLAB (The MathWorks, Natick, MA, USA) and R (R Core Team). We focused our analyses on Pre- and Post-training sessions only, which were identical for all participants. For the dependent measure of accuracy of perceptual decisions, means were calculated for each condition (for each Signal Range condition, separately for Pre- and Post-training) at the participant level. Where Mauchly’s test indicated a violation of the assumption of sphericity, p-values are reported after adjustment using the Greenhouse-Geisser method, indicated by pGG.

Collapsing across factors of Group, Signal Range, and Session (Pre- and Post-training), mean accuracy was 74.8% (between-subjects SD 7.2%), confirming that our staircasing procedure was effective (target of 75% accuracy), and mean response time was 720.9 ms with a between-subjects SD 360.1 ms, revealing high variability between participants in their response time (note that participants were not instructed to respond quickly). Mean confidence rating was 2.6 (4-point scale; between-subject SD 0.7). Accuracy and Confidence Rating data are shown in Fig. 2A for Pre- and Post-training sessions, and Fig. 2B for training sessions. During training (averaging across sessions 2, 3 and 4) mean accuracy was 74.4% (between-subjects SD 7.4%), again confirming that the staircasing procedure was effective.

Fig. 2
figure 2

(A) Results from Pre- and Post-training. Confidence Rating (top) and accuracy (bottom) data are shown as a function of Signal Range, for the three experimental groups. The effect of Signal Range on Confidence Ratings was attenuated following training. (B) Data from the training sessions. Confidence Rating (top) and accuracy (bottom) data are shown as a function of Signal Range, for the three experimental groups. Note that individual participants in the Fixed Range + Feedback group were allocated to a single Signal Range level during their training sessions, and thus there were only six participants per Signal Range condition in this group, whereas each participant in the Variable Range + Feedback and Variable Range No Feedback groups contributed data to all Signal Range levels. Error bars indicate within-subject standard error, with the exception of data from the Fixed Range + Feedback group in panel B (training sessions), which show between-subjects standard error

Full size image

We first evaluated the hypothesis concerning training, that the extent to which Signal Range affects Confidence Ratings would be reduced at Post-training relative to Pre-training. Using the ‘ez’ package (Lawrence & Lawrence, 2016) implemented in R, we conducted an ANOVA with a repeated-measures factor of Signal Range (±5°, 10°, 20°, 30°), a repeated-measures factor of Session (Pre-training, Post-training), and a between-subjects factor of Group (Variable Range + Feedback, Fixed Range + Feedback), on Confidence Ratings (focusing on the interaction between Signal Range and Session on Confidence Ratings, with or without an interaction with Group). This analysis was included in our initial preregistration, and was therefore evaluated by analysing data from the first two experimental groups (Variable Range + Feedback, Fixed Range + Feedback). We found a significant two-way interaction between Signal Range and Session, on Confidence Ratings, F(3, 141) = 4.564, pGG = .007, ηp2 = 0.089 (Fig. 2A). Following up, the effect of Signal Range on Confidence Ratings was significant prior to training, F(3, 144) = 21.612, pGG < .001, ηp2 = 0.310, replicating previous studies (Spence et al., 2016; Spence et al., 2018), but no longer reached significance following training, F(3, 144) = 3.127, pGG = 0.050, ηp2 = 0.061.

We also conducted an equivalent Bayesian analysis, implemented in R using the ‘BayesFactor’ package (Morey, Rouder, & Jamil, 2015; Rouder, Morey, Speckman, & Province, 2012). The Bayesian analyses allowed us to assess both whether there was evidence in support of the alternate model, as well as whether there was evidence in support of the null model, as indicated by BF10 values. Prior to data collection, we specified a cut-off of a BF10 > 3 as evidence for the alternate hypothesis over the null, and BF10 < 0.333 as evidence for the null hypothesis over the alternate. To evaluate the interaction between Signal Range and Session, we calculated the Range effect at Pre- and Post-training, collapsed across the two experimental groups, as the difference between Confidence ratings for the 5° and 30° Range conditions. We then compared these with a Bayesian repeated-measures t-test. This test yielded a BF10 of 7.391, indicating strong evidence in favour of a change in Range effect on Confidence ratings from Pre- to Post-training. Following up, the effect of Range on Confidence was greater prior to training (BF10 = 6.054e+8) than following training (BF10 = 1.108).

The above analysis also addressed an additional hypothesis concerning the form of training, in which we tested for non-directional group differences in training, between the two groups specified in our initial preregistration. Here, the three-way interaction between Signal Range, Session, and Group was not significant, F(3, 141) = 0.326, pGG = .772, ηp2 = 0.007 (Fig. 2A). To evaluate the three-way interaction using Bayesian statistics, we calculated the change in Range effect from Pre- to Post-training for the two groups, and compared this with a Bayesian independent groups t-test (BF10 = 0.309; note that this was our stopping rule). Thus, the weight of the evidence suggests that both groups showed similar effects of training, with Signal Range having a reduced influence on Confidence in the Post-training session.

We were also interested in whether the relationship between Response Time and Confidence Ratings would be attenuated at post-training relative to pre-training. To test this, we calculated the Spearman correlation coefficient between Response Time and Confidence Ratings for each participant in Groups 1 and 2, separately by Signal Range condition, and separately for Pre- and Post-training. Three participants were excluded from this analysis, because there was no variability in their Confidence ratings in at least one cell, and therefore correlations could not be calculated. In Session 1, the majority of participants showed a significant negative correlation between RT (response time) and Confidence (collapsed across Signal Range conditions; range: -.602 to .637, mean = -.221; significant correlations for 41 out of 49 participants; Fig. 3A). This negative relationship was also present in Session 5 (range: -.750 to .257, mean = -.207; significant correlations for 42 out of 49 participants; Fig. 3A.

Fig. 3
figure 3

(A) Histograms showing the distribution of subject-level Spearman’s correlation coefficients for the relationship between Confidence ratings and response time (RT) (collapsed across Signal Range levels; Variable Range + Feedback and the Fixed Range + Feedback groups), at Pre- and Post-training. (B) Group-level summary data for RT – Confidence correlations, plotted separately for each Signal Range condition. The relationship between Response Time and Confidence was not affected by training. Error bars indicate within-subject standard error

Full size image

We conducted an ANOVA with a repeated measures factor of Signal Range (±5°, 10°, 20°, 30°), a repeated-measures factor of Session (Pre-training, Post-training), and a between-subjects factor of Group (Variable Range + Feedback, Fixed Range + Feedback), on the RT-Confidence correlation coefficients. We found no evidence that training changed the relationship between Response Time and Confidence (Fig. 3B). The effect of Session on the RT-Confidence correlation was not significant, F(1, 44) = 0.780, p = .382, ηp2 = 0.017, BF10 = 0.229, nor were the interactions between Session and Group, F(1, 44) = 1.091, p = 0.175, ηp2 = 0.024, BF10 = 0.628 (equivocal), Session and Range, F(3, 132) = 1.423, p = 0.239, ηp2 = 0.031, BF10 = 0.355 (equivocal). The three-way interaction between Session, Group, and Signal Range was also not significant, F(3, 132) = 0.586, p = .625, ηp2 = 0.013, and Bayesian analysis revealed equivocal evidence for the null and alternate hypotheses (BF10 = 0.374).Footnote 1

We next tested a directional hypothesis that if training improves the quality of confidence judgements, we should see an improvement in meta-d’ from Pre- to Post-training (main effect of Session on meta-d’, with or without interactions with Signal Range or Group). Participant-level estimates of metacognitive efficiency were modelled based on accuracy of responses and confidence ratings, using a hierarchical Bayesian implementation in Matlab (HMeta-d; Fleming, 2017). Meta-d’ estimates were modelled separately for each Signal Range condition, at Pre- and Post-training. We conducted an ANOVA with a repeated-measures factor of Signal Range (+/-5°, 10°, 20°, 30°), a repeated-measures factor of Session (Pre-training, Post-training), and a between-subjects factor of Group (Variable Range + Feedback, Fixed Range + Feedback), on meta-d’ (Fig. 4). The effect of Session on meta-d’ was not significant, F(1, 47) = 0.308, p = .582, ηp2 = 0.007, BF10 = 0.180, nor were the interactions between Session and Group, F(1, 47) = 0.090, p = 0.766, ηp2 = 0.002, BF10 = 0.296, Session and Range, F(3, 141) = 0.549, p = 0.650, ηp2 = 0.012, BF10 = 0.174. The three-way interaction between Session, Group, and Signal Range was also not significant, F(3, 141) = 1.929, p = .128, ηp2 = 0.039, and the Bayesian analysis revealed equivocal evidence for the null and alternate hypotheses (BF10 = 1.272). Thus, we did not find evidence that training improved the quality of metacognitive efficiency.

Fig. 4
figure 4

Meta-d’ – a metric of metacognitive efficiency – as a function of Signal Range, for the Variable Range + Feedback and the Fixed Range + Feedback groups, at Pre- and Post-training. Training had no effect on metacognitive efficiency. Error bars indicate within-subject standard error

Full size image

Based on the above results showing evidence for a training effect on confidence that was similar for both groups, we preregistered a third experimental group to add to our study design. This third group (Variable Range No Feedback) completed the same protocol as the Variable Range + Feedback Group, but they did not receive trial-by-trial feedback during training. We included this group to assess whether feedback during training was necessary to attenuate the effect of Signal Range on Confidence ratings.

Including data from all three groups (Fig. 2), the interaction between Signal Range and Session on Confidence ratings was again significant, F(3, 210) = 4.842, p = .003, ηp2 = 0.065. The equivalent Bayesian analysis yielded a BF10 of 11.504, providing strong evidence that the effect of Signal Range on Confidence ratings was reduced following training. As with the subset of data that we had analysed previously, the effect of Signal Range on Confidence was stronger prior to training, F(3, 216) = 32.996, pGG < .001, ηp2 = 0.314, BF10 = 3.740e+14 (again replicating previous demonstrations of the effect of Signal Range on Confidence: Spence et al., 2016; Spence et al., 2018), than following training, F(3, 216) = 7.096, pGG < .001, ηp2 = 0.090, BF10 = 121.757. We did not find evidence for group differences in this training effect – the three-way interaction between Signal Range, Session, and Group, including all three groups, was not significant, F(6, 210) = 0.561, p = .761, ηp2 = 0.016, BF10 = 0.235. Thus, the attenuated influence of Signal Range on Confidence following training appears to be consistent across the three experimental groups, suggesting that the presence of variable signal range during training, nor the provision of trial-by-trial accuracy feedback during training, were necessary for driving the observed training effects.

Discussion

Sensory uncertainty has been shown to impact confidence estimation, even in cases where it is irrelevant for the perceptual decision on which the confidence judgement is based (Spence et al., 2016; Spence et al., 2018). The current study aimed to investigate whether the influence of sensory variability on confidence could be reduced through training. Replicating these previous studies, we found an inverse relationship between the range of motion direction signals and confidence ratings following direction comparison judgements. Importantly, this effect was significantly reduced following three days of task training. The reduced effect of signal range on confidence was unaffected by the presence (or absence) of variability during training, as well as the provision (or exclusion) of feedback on perceptual performance. Interestingly, this change in confidence estimation did not translate to an improvement in metacognitive efficiency.

Although the variability of sensory signals can indeed impact performance (de Gardelle & Summerfield, 2011), relying on sensory variability as a heuristic when making confidence judgements can lead to suboptimal metacognitive performance (Allen et al., 2016; de Gardelle & Mamassian, 2015; Spence et al., 2016; Spence et al., 2018). Under certain circumstances, increasing sensory variability can even lead to opposing effects on first-order performance and confidence (Rahnev et al., 2012; Zylberberg et al., 2016; Zylberberg et al., 2014). Similarly, Maniscalco, Peters, and Lau (2016) discuss how another heuristic to confidence – discounting evidence against a perceptual choice in favour of evidence for the perceptual choice – can also lead to suboptimal performance, despite being a potentially good strategy in naturalistic decision-making, where evidence against a perceptual choice may be ambiguous. In our results, we provide evidence that the susceptibility of confidence judgements to heuristic biases can be reduced through task practice, suggesting that the metacognitive system is malleable, adapting according to the perceptual demands faced by an individual.

Interestingly, the shift in the impact of signal variability on confidence that we observed occurred regardless of whether participants were exposed to fixed or varying signal range levels during their training sessions, and regardless of whether they received feedback on their perceptual performance. This might suggest that mechanisms underlying confidence estimation adapt relatively automatically through practice on a task, rather than being an explicit strategic shift driven by task demands or context. We did not observe training-related changes in the relationship between response time and confidence. Importantly, we manipulated signal range while controlling accuracy via a staircasing procedure, which allowed us to dissociate the effect of signal range on confidence from the effect on accuracy. We did not exert the same level of experimental control over the concordance between response time and accuracy, which may account for the consistent relationship between response time and confidence, despite training. If the observed training effects on signal range in the current study depend on exposure to confidence heuristics that are experimentally manipulated to be suboptimal, similar results may be observed for response time if this is also manipulated experimentally (akin to Kiani et al., 2014, for example, in a training protocol similar to the current design).

We found no evidence of improvement in metacognitive efficiency, across all experimental groups: although our participants were less biased in their overall level of confidence according to the variability of direction signals following training, at the level of individual decisions, participants made just as many mischaracterisations in their confidence estimation following training. Counter to these results, a recent study has provided evidence that training can lead to enhanced metacognitive insight (Carpenter et al., 2019). A key aspect of Carpenter and colleagues’ design is that their training protocol provided feedback based specifically on confidence estimation (second-order) ability, in a block-wise fashion, rather than feedback based on perceptual (first-order) ability. In contrast, we opted to provide more fine-grained, trial-by-trial feedback, which necessarily relates to both perceptual and metacognitive performance. Interestingly, improvement to metacognitive insight was specific to the coarser (block-wise) metacognitive feedback given to Carpenter and colleagues’ participants, and was not observed for a control group who received block-wise feedback on perceptual performance.

Additionally, by using online data collection through Amazon’s Mechanical Turk, Carpenter and colleagues’ design was able to include eight training sessions (compared with our three training sessions), leaving open the possibility that a longer period of training, either in overall timeframe or number of trials, might be necessary to elicit shifts in metacognitive insight. In fact, the authors report that shifts in metacognitive bias emerged first during training, and were followed later by (and were predictive of) improvements in metacognitive insight. This work provides the foundation for developing interventions to improve metacognitive ability in applied environments. However, our own results suggest that training metacognition is not straight-forward, and factors such as the form of feedback provided and the duration of training might be critical in enhancing metacognitive insight, beyond reducing the impact of suboptimal heuristics to confidence.

Metacognition has been proposed as an important self-regulatory process, aiding learning and performance, and interventions that can improve metacognitive processes therefore have potentially widespread applications across domains involving human performance (Callender, Franco-Watkins, & Roberts, 2016; Mamassian, 2016; Meyniel, Sigman, & Mainen, 2015). Our results reveal that the dynamics of factors influencing confidence estimation change with practice on a task. This shift occurs regardless of whether a variable or stable environment is experienced during practice, and regardless of whether performance feedback is available during practice. However, we did not observe improvements to metacognitive insight – our training protocol did not affect an individual’s ability to differentiate between correct and incorrect responses via their confidence estimation. This opens the door for future research to continue to investigate the dynamics of the computation of confidence, particularly the flexibility of metacognitive processes to adapt to factors that have the potential to contaminate confidence estimation.