Introduction

Visual masking is defined as the reduction of visibility of one stimulus (target) by another stimulus (mask) when the mask is presented in the spatio-temporal vicinity of the target (Bachmann, 1994; Breitmeyer & Ogmen, 2006). Visual masking has largely been investigated as a phenomenon reflecting the spatiotemporal dynamics of the visual system, and it provides a useful tool to study differences between nonconscious stimulus- and conscious percept-dependent visual processing. Several types of masking have been identified that depend on the spatiotemporal characteristics of the stimuli. When the target is followed by the mask in time, it is referred to as backward masking whereas when the mask precedes the target, it is called forward masking. Moreover, when the target and mask onsets coincide but the mask outlasts the target, it is called common-onset asynchronous-offset masking (henceforth it will be called common-onset masking). In terms of spatial properties, backward masking is referred to as metacontrast masking when the target and mask stimuli do not spatially overlap.

In terms of information processing, it is known that visual masks can suppress, or “erase,” the contents of sensory (or iconic) memory, which is a large capacity and rapidly decaying store (Averbach & Sperling, 1961; Haber, 1983; Sperling, 1960). The control of the contents of sensory memory by masking mechanisms has two important functional implications: First, since the contents of sensory memory are encoded in retinotopic coordinates, based on the duration of the visible-persistence component of sensory memory, moving objects should appear highly smeared. Empirical and computational evidence shows that, by suppressing the contents of sensory memory, visual masking mechanisms play an important role in establishing the clarity of our vision for moving objects (Chen, Bedell, & Ogmen, 1995; Noory, Herzog, & Ogmen, 2015; Ogmen, 1993; Purushothaman, Ogmen, Chen, & Bedell, 1998). Second, a subset of the contents of sensory memory is transferred to a more durable but low-capacity store, called visual short-term memory (VSTM) (Atkinson & Shiffrin, 1971; Averbach & Sperling, 1961). One of the distinguishing properties of VSTM from sensory memory is its immunity to visual masking (e.g., Averbach & Coriell, 1961; Gegenfurtner & Sperling, 1993; Haber, 1983; Loftus, Duncan, & Gehrig, 1992; Schill & Zetzsche, 1995). Hence, visual masking plays an important functional role in controlling which information will be available for transfer to VSTM.

Another process known to control the transfer of information from sensory memory to VSTM is attention (e.g., Gegenfurtner & Sperling, 1993; Makovski & Jiang, 2007; Ogmen, Ekiz, Huynh, Bedell, & Tripathy, 2013; Palmer, 1990; Sreenivasan & Jha, 2007; Tombu et al., 2011). Since both attention and visual masking control (i.e., modulate) the transfer of information from sensory memory to VSTM, a natural question is whether these processes operate independently or they interact with each other. From a theoretical point of view, determining whether these two processes interact or not can contribute to our understanding of how information is transferred from sensory memory to VSTM. From an empirical point of view, this understanding is especially important when one wants to compare findings from different studies of VSTM, which employ different types of masks or masks with different strengths. If, indeed, masking and attention do interact, reconciliation or comparison of findings across different studies will require one to take into account the interaction effects.

Determining whether masking and attention interact also has important implications for theories of visual masking. Selective attention has facilitative, as well as inhibitory, effects in almost all perceptual tasks and regardless of criterion contents (Posner, 1980; Smith, Ratcliff, & Wolfgang, 2004). However, many early theoretical models of masking do not include a term or a mechanism for the effects of attention, implying that these models assume that attention and masking are independent processes (e.g., Bachmann, 1984; Breitmeyer & Ganz, 1976; Bridgeman, 1971; Francis, 2000; Ogmen, 1993; Weisstein, Ozog, & Szoc, 1975). This does not necessarily mean that these models dismiss the role of attention. Attention can be incorporated into these models largely as an add-on process, which adds to the masking strength, or reduces it, depending on the locus of attention or attentional load. In fact, Michaels and Turvey (1979) incorporated attention in their model as an independent process working in conjunction with spatial inhibitory processes.

On the other hand, at least one theory of visual masking considers attention as an essential component and predicts interactions between masking and attention (Di Lollo, Enns, & Rensink, 2000; Enns & Di Lollo, 1997). In a common onset masking paradigm, Enns and Di Lollo (1997) used a diamond shaped stimulus as target and four surrounding dots as mask. They found that the four-dot mask can produce strong masking effects when the stimuli were viewed peripherally and when attention could not be focused on a certain target location (i.e., with set sizes larger than one). Enns and Di Lollo attributed these effects to higher-level processes of object substitution. Here, the assumption is that, as set-size increases, attentional resources will have to be spread over more locations, thereby increasing the attentional load and, hence, the time it takes for focused attention to arrive at the target’s location. On the other hand, when set-size is small or when the target just “pops out,” attention quickly focuses on this location. If attention arrives to the location of the target before re-entrant signals feed back to the target’s location, the observer will be able to perceive and identify the target. On the other hand, if re-entrant signals arrive at the target’s location before attention, a mismatch between the re-entrant visual representation of the target-mask pair and the incoming lower level activity due to mask alone (since it is presented alone after target’s offset) will occur. In this case, the mask-only representation will substitute in perception the early activities generated by the target-mask pair. In summary, interaction between attention and masking is an essential ingredient of the object substitution theory. This prediction was supported by significant interaction effects found in their study (Di Lollo et al., 2000; Enns & Di Lollo, 1997).

Reports of interactions between masking and attention have not been limited to the common-onset masking paradigm, but also included metacontrast masking (Ramachandran & Cobb, 1995; Shelley-Tremblay & Mack, 1999; Tata, 2002). Hence, a question arises as to whether theories of metacontrast masking should include attention as an essential component.

However, more recent evidence shows that, in common-onset masking with four-dot masks, masking strength and set size (i.e., attention), do not actually interact, and that previous studies suffered from ceiling and/or floor effects which led to an artifactual appearance of interactions (Argyropoulos, Gellatly, Pilling, & Carter, 2013). This finding has been recently replicated by using an eight-alternative forced-choice task (Filmer, Mattingley, & Dux, 2014), providing further evidence against the attention account of object-substitution theory. Pilling et al. (2014) also employed a spatial cue to directly control spatial attention, and also reported no interaction. Filmer, Mattingley, and Dux (2015) have also demonstrated strong common-onset masking for the attended and foveated targets, which strongly contradicts the object-substitution account of common-onset masking. Given these findings, we have examined whether the reported interactions between attention and metacontrast may also be artifacts of ceiling and/or floor effects. The objective of the present study was to investigate whether metacontrast masking and attention interact by using an experimental design in which saturation and floor effects are avoided. We asked observers to report the orientation of a target bar when presented with other randomly tilted distractor bars. By adjusting stimulus parameters for each observer such that both the ceiling and floor effect are avoided, we investigated the relationship between masking and attention at two different levels: (i) in mean absolute response errors and (ii) in distribution of signed response errors. Our results show that although attention affects observer’s performance, its effect does not interact with masking. Statistical modeling of response errors suggests that attention and masking exert their effects by independently modulating the probability of “guessing” behavior.

Methods

Participants

Seven observers participated in this study. Five of them were naïve as to the purpose of the experiment. Participants reported normal or corrected-to-normal vision and gave written informed consent before the experiments. All experiments were carried out in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki), and followed a protocol approved by the University of Houston Committee for the Protection of Human Subjects.

Apparatus

Visual stimuli were created using the ViSaGe and VSG2/5 cards manufactured by Cambridge Research Systems. Stimuli were displayed on a 22-in. CRT monitor with a refresh rate of 100 Hz and display resolution of 800 by 600 pixels. The distance between the display and the observer was 1 m, and a head/chin rest was utilized to restrict movements of the observer. Observers responded via a joystick after each trial.

Stimuli and procedures

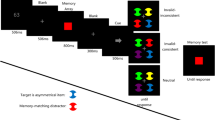
In each trial, several oriented bars (1° long, 0.1° wide) with centers equidistant from the display center were presented briefly (10 ms). Any one of the bars could potentially be the target stimulus, and the target was specified by the mask location, which was a non-overlapping ring having 1.1° inner and 1.4° outer diameters, respectively. In other words, only one mask stimulus was presented and its location cued which oriented bar is the target. The other bars will be referred to as distractors from here on in. The task of the observers was to report the orientation of the target bar. Figure 1 illustrates the stimuli and procedures. A trial starts with a black (nominally 0 cd/ m2) fixation spot at the center of a blank white screen (60 cd/m2). After a random time interval (500–1,000 ms), an array of randomly oriented bars at equal eccentricities was presented around an imaginary circle (with a radius of 6°). After an SOA interval (0–200 ms), a spatially non-overlapping mask stimulus (a ring) was presented. Within the same block, a small square (rather than a mask) indicated the location of the target bar in some of the trials. The trials in which a small square was presented were considered as baseline trials. The duration of the target and mask was 10 ms (one frame). The luminance of the target and mask was adjusted individually for each observer to avoid floor and ceiling effects. Once the target-mask sequence was presented and turned off, a randomly oriented (response) bar was displayed at the center of the screen, and observers adjusted its orientation (illustrated by red arrows in Fig. 1) via a joystick to match the target bar’s orientation. The response bar stayed on the display until observers were satisfied with their responses and the next trial began with another button press. In a separate blocks, we presented an array with two or six oriented bars. Varying the set size allowed us to determine the effect of attention and its interaction, if any, with masking.

Fig. 1
figure 1

Time course of the stimuli. A trial began with a fixation spot at the center of the display. After a variable time interval an array of oriented bars was presented for 10 ms. This was followed by a blank screen the duration of which was set according to a variable stimulus onset asynchrony (SOA). The sequence continued either with (A) a mask stimulus (a ring), or (B) a small square (a post-cue) which were presented for 10 ms. Finally, a randomly oriented bar was presented at the center of the screen. The task of the observers was to report the orientation of the masked (or probed) bar by adjusting the orientation of this central bar via a joystick. The red arrows in the last frame are for illustration purposes, and they were not presented as part of the stimulus

Full size image

We defined response errors as the difference between the actual and reported orientations. Error values ranged from −90 to 90°. We obtained masking functions after transforming response errors to a probability-like measure such that performance values of 0.5 and 1 correspond to chance and perfect performance, respectively. We calculated transformed performance (Ogmen et al., 2013) as:

$$ Transformed\ performance=1 - \frac{\left| Error\ angle\right|}{90} $$
(1)

When the observer can report the orientation of the target bar veridically, then error angle will be zero, which corresponds to a transformed performance value of 1. When the observer randomly guesses, the absolute value of the response error will be distributed uniformly within the range of 0 and 90°. Hence, the average of the absolute value of error angles will be 45° with the corresponding transformed performance value equal to 0.5.

For the purpose of this study, ceiling and floor effects must be avoided. The floor can be defined as the chance level, which corresponds to 0.5 transformed performance (see Eq. 1), and the ceiling can be defined as the maximum performance an observer can possibly achieve in the absence of a mask. Thus, one has to determine the ceiling level (i.e., baseline performance in the absence of a mask) for each and every observer by presenting the target stimulus only. However, since we present an array of oriented bars rather than a single one, one needs to specify which one of them is the target without affecting its visibility. Moreover, obtaining the baseline performance at a single SOA may not be appropriate, since there may be additional confounding factors (such as memory leakage especially at long SOAs). Therefore, we presented a small square (0.2 × 0.2°) as a cue in the spatial vicinity of the target bar at each SOA. This way we had a separate baseline performance for each SOA, and we made sure that the ceiling effect is avoided at each SOA.

Before the actual experiments, we first trained the observers with two or three blocks of trials with all conditions to make sure that they became familiar with the experiment and the setup so as to stabilize their performance and minimize changes due to learning. In order to avoid the ceiling and floor effects described above, we adjusted two parameters: the target luminance and the mask luminance. The criteria that we used to obtain the target and mask luminance values were as follows:

  1. C1)

    The maximum performance with masking must be significantly lower than the baseline performance (the ceiling) when set size is two.

  2. C2)

    The minimum performance with masking must be significantly higher than chance level (the floor, i.e., 0.5 transformed performance).

Based on pilot experiments and our previous studies on metacontrast masking, we carried out a power analysis to select the number of trials per SOA for masking and baseline (i.e., without a mask) conditions. Power analysis is necessary to assess Type-II errors (i.e., probability of falsely accepting a null hypothesis). Therefore, we determined the number of trials required to reject the null hypothesis (i.e., the transformed performances with and without a mask are equal) by a two-sample t-test with a power level larger than 0.7. In a previous study, we found that the average standard deviation of transformed-performance across observers is roughly 0.15 (Agaoglu et al., 2015). We also found small-to-moderate effect sizes (defined as the difference between two conditions divided by the standard deviation of one group (Cohen, 1988)) between baseline and weak masking conditions. Therefore, we assumed a small effect size (i.e., between 0.1 and 0.3) in the present study. This analysis yielded roughly 200 trials per SOA value in total. Therefore, each observer ran 125 masking trials and 75 baseline trials per SOA. Table 1 summarizes the target-mask luminance pairs for all observers as well as the results of statistical tests to verify that the aforementioned criteria (C1 and C2) are met.

Table 1 The target, mask, and cue luminance values in cd/m2 (and corresponding Weber contrasts) for each observer. The background luminance was set to 60 cd/m2 for all observers. The results of t-tests used to determine whether criteria C1 and C2 are met are also listed. Note that we used two-sample t-tests with unequal variances for testing for C1, and one-sample t-tests against chance level (0.5)
Full size table

Since masking strength is observer-dependent, the same set of parameters for all observers may not avoid floor and ceiling effects. For this reason, we adjusted target and mask luminance values individually for each observer to make sure that the data were free of floor and ceiling effects. Moreover, changing target and mask luminance does alter the location of maximum masking and may even result in Type-A (i.e., maximum masking at 0-ms SOA and monotonic increase in performance for positive SOAs) or Type B (i.e., maximum masking at a positive SOA and minimal or no masking at 0-ms SOA and beyond 300-ms SOA) masking functions depending on the observer. Therefore, the luminance values should be adjusted for each observer separately in order to produce Type-B masking functions, a prominent signature of metacontrast masking, for each observer. In order to capture the “U-shaped” masking functions from each and every observer, we needed to select a different set of SOA values.

Once we established a set of parameters, which satisfied all the criteria given above, we analyzed transformed-performance of each observer separately (within-subject analysis). We fitted a series of linear and polynomial regression models to pin down the presence/absence of contributions of the main factors and their interactions. Table 2 lists all regression models used to fit the data. We used Bayesian Information Criterion (BIC) and Adjusted R2 metrics for selecting the best model. Both metrics resulted in similar, if not identical, model selections for all observers. Both metrics penalize the models with more free parameters. Absolute values of BICs are not meaningful, therefore one needs to look at differences between BICs from different models. A BIC difference of x between model A and model B (i.e., BICA − BICB) corresponds to e-x-to-1 odds favoring model A. Therefore, the smaller the BIC, the better the model performs. According to Jeffreys’ scale of interpretation (Jeffreys, 1998), an odds ratio lower than one (i.e., e-x < 1) supports the null hypothesis, whereas an odds ratio larger than one (i.e., e-x > 1) supports the alternative hypothesis. Values larger than 100 (e-x > 100) are considered as a sign of “decisive evidence” against the null hypothesis, and similarly, values smaller than 0.1 (i.e., e-x < 0.1) are interpreted as “strong evidence” against the alternative hypothesis.

Table 2 The regression models used to fit transformed performances and the winning model parameters. The models are sorted based on number of parameters. The models M1, M2, M3, M4, M7, M8, M9, and M14 are the standard linear regression models whereas the remainder of the models have quadratic main factors and/or interactions
Full size table

Statistical modeling of response errors

We examined the distribution of response errors of observers to understand how attention and masking exert their effect on performance. We adopted the statistical models that have been previously used in modeling VSTM (Bays, Catalao, & Husain, 2009; Zhang & Luck, 2008) and several visual phenomena such as crowding (Ester, Zilber, & Serences, 2015) and masking (Agaoglu, Agaoglu, Breitmeyer, & Ogmen, 2015; Harrison, Rajsic, & Wilson, 2014). The simplest model is a single Gaussian (referred to as the G model from now on) whose mean and standard deviation may be modulated by attention and/or masking. The mean of Gaussian represents how accurately the target orientation is encoded by the visual system. Non-zero values indicate observer bias in responses. The mean of the target Gaussian was set to zero, i.e., centered on target orientation. This was motivated by our recent study on masking where we found that the mean of the Gaussian is not significantly different from zero (Agaoglu et al., 2015). Therefore, in the following analyses, the target Gaussians were centered on target orientations (i.e., zero mean in error space). The reciprocal of standard deviation represents how precisely the stimulus falling onto the retina is encoded by the visual system. In other words, decreased stimulus encoding precision is reflected by the increased variability of behavioral responses.

In the second model, Gaussian + Uniform (the GU model), the additional Uniform component represents the “guess rate.” The increased guess rate is modeled by the weight of the uniform distribution. The GU model is a weighted sum of Gaussian and Uniform distributions (Eq. 2):

$$ PDF\left(\varepsilon \right) = {w}_G*G\left(\mu, \sigma \right) + \left(1-{w}_G\right)*U $$
(2)

where PDF(ε) represents the distribution of response errors, and w G represents the weight of the Gaussian term with mean and standard deviation given as μ and σ.

Since the stimulus display consists of multiple oriented bars, observers may report the orientation of one of the non-target bars, e.g., the one that has the closest angle to the target angle (the GU + Closest Angle model or in short, the GUCA model), or the closest location to the target location (the GU + Nearest Neighbor or in short, the GUNN model), instead of the target bar. The contribution of this incorrect identity binding error can be captured by another Gaussian term in the model. In consequence, the PDF of response errors can be written as a weighted sum of the target Gaussian, non-target Gaussian, and a uniform component (Eq. 3) (Bays et al., 2009).

$$ PDF\left(\varepsilon \right)={w}_TG\left({\mu}_T,{\sigma}_T\right) + {w}_{NT}G\left({\mu}_{NT},{\sigma}_{NT}\right) + \left(1-{w}_T-{w}_{NT}\right)U\left(-\pi /2,\pi /2\right), $$
(3)

where subscripts T and NT represent target and non-target parameters, respectively.

Model fitting and model comparison

We used the Bayesian Model Comparison (BMC) technique (Mackay, 2004; Wasserman, 2000) for selecting the best fitting model. Each model m j produces a conditional probability p(ε|m j , θ), where ε is a vector of observed response errors, and θ is a vector of model parameters. For each model, we calculated the probability of finding observed response errors, averaged over free parameters:

$$ L\left({m}_j\right)\ \triangleq p\left(\varepsilon /{m}_j\right)={\displaystyle \int }p\left(\varepsilon \Big|{m}_j,\theta \right)p\left(\theta \Big|{m}_j\right)d\theta ={\displaystyle \int}\left({\displaystyle {\prod}_{i=1}^Np\left({\varepsilon}_i\Big|{m}_j,\theta \right)}\right)p\left(\theta \Big|{m}_j\right)d\theta, $$
(4)

where N represents the number of trials and εi represents the error in the ith trial. It is convenient to take the logarithm of Eq. 4 in order to compute it numerically. Eq. 4 can be rewritten as

$$ \ln\;L\left({m}_j\right)= \ln\;{L}_{max}\left({m}_j\right)+ \ln \left[{\displaystyle \int } exp\left( \ln L\left({m}_j\Big|\theta \right)- \ln {L}_{max}\left({m}_j\right)\right)p\left(\theta \Big|{m}_j\right)d\theta \right], $$
(5)

where ln L(m j |θ) = ∑ N i = 1 ln(p(ε i |m j , θ), and L max (m j ) = max(L(m j |θ)). Parameters corresponding to L max (m j ) can be regarded as the Maximum Likelihood Estimation (MLE) of the model parameters for model m j . Subtracting L max (m j ) ensures that the exponential in the integrand is of order 1 and thereby avoids numerical problems (Ester et al., 2015; Mackay, 2004; van den Berg, Shin, Chou, George, & Ma, 2012). We used uniform priors for all parameters over plausible ranges (see Table 2).

Considering these priors, Eq. 5 becomes

$$ \ln\;L(m)= \ln\;{L}_{max}(m)-{\displaystyle {\sum}_j^k \ln \left({R}_j\right)+ \ln \left[{\displaystyle \int } exp\left( \ln L\left(m\Big|\theta \right)- \ln {L}_{max}(m)\right)d\theta \right]}, $$
(6)

where R j represents the size of the range for jth free parameter. We approximated the integral by a Riemann sum with at least 50 bins in each parameter dimension (see Table 3). The performance metric given in Eq. 6 will be referred to as the BMC. The difference between the BMCs from two different models is equivalent to the logarithm of likelihood ratios of them. Therefore, a model with larger BMC is a better model. We used Jeffrey’s scale of interpretation for comparing BMCs from different models. A BMC difference of x between model A and model B corresponds to ex-to-1 odds favoring model A.

Table 3 Range of parameters used for Bayesian Model Comparison (BMC). Note that in a separate analysis, we used step sizes of 0.1 for standard deviation of the Gaussian, and 0.002 for the weight of the Uniform for the Gaussian + Uniform (GU) model but the winning model and the pattern of changes in model parameters were not affected by this change
Full size table

Analysis of model parameters

After selecting the best fitting model, we sought to find how different model parameters change with SOA and set size. The motivation behind this analysis was to understand whether and how masking and attention affect the statistics of observer responses. After determining the winning model, we created 500 different data sets (for each observer separately) by resampling the response errors by replacement, and fitted the winning model to these data sets. We present here the means and standard errors for model parameters obtained from this bootstrap analysis. Next, we fitted the regression models listed in Table 2 to see the contributions of SOA, set size, and their interactions to model parameters.

In order to determine whether masking strength and different model parameters are related or not, we also quantified the correlation between model parameters and masking function for each set-size by calculating Pearson R coefficients. A strong correlation would suggest a critical role for that parameter in accounting for masking effects, and a change in correlation with set size would suggest an interaction between attention and masking.

Results

Psychophysics

Figure 2 shows results from all observers. The vertical axes represent the transformed performance while the horizontal axes represent SOA between the target and mask (or cue in the baseline conditions) stimuli. Open and filled symbols correspond to the baseline and masking conditions, respectively. Circles and squares plot the results for set-size of two and six, respectively. Consider first the baseline data.Footnote 1 Our goal in collecting the baseline data was to ensure that the masking data did not have any ceiling effect (criterion C1, see Methods). For each observer, we performed a two-sample t-test between baseline and masking conditions at an SOA value where minimum masking occurs (e.g., typically 0 ms SOA with set size 2). For all observers, transformed performance was significantly smaller in the masking condition (p < 0.05). In addition to ceiling effects, we have also checked our data for floor effects (criterion C2, see Methods) by performing a one-sample t-test against the chance level (i.e., 0.5 transformed performance) at SOA values where masking is strongest. We confirmed that transformed performance was significantly larger than the chance level (p < 0.05) for all observers even when masking is strongest. Table 1 lists the target-mask luminance pairs which allowed us to avoid ceiling and floor artefacts for each observer, as well as the results of the t-tests. Taken together, these results show that our masking data are free of ceiling and floor effects.

Fig. 2
figure 2

The left column shows transformed performance for each observer against stimulus onset asynchrony (SOA). The red open and filled circle symbols represent performance in baseline and metacontrast masking, respectively, when set-size is two, whereas the blue open and filled square symbols represent performance in baseline and metacontrast masking, respectively, with set-size six. With the same color convention, solid and dashed lines represent the best regression fits for metacontrast masking and baseline conditions, respectively. Chance level is 0.5 transformed performance. Error bars represent ± SEM across trials (n=125 for masking, n=75 for baseline). The right column shows pairwise Bayesian Information Criterion (BIC) differences between regression models listed in Table 2 in explaining transformed performances. A square with coordinates (x,y) on each plot represents the BIC difference between model x and y (i.e., BICMx − BICMy). The smaller the BIC, the better the model performs, therefore negative values (i.e., cooler colors) represent better model performance. Model M16 was the best model for all observers. Note that adding more terms to model M16 does not improve model performance, which is evident by dark blue bands formed in the lower left quadrant of each plot

Full size image

Do masking and attention interact?

We fitted a series of polynomial regression models (in addition to the standard linear regression models) to each observer’s data to determine whether SOA and set size and their interaction have any significant contribution to transformed performance. Figure 2 (the right column) shows pairwise model comparison results based on the BIC metric. Greenish colors represent equivalent performances whereas blue and red colors represent better and worse model performances, respectively. As evident from Fig. 2, the models with quadratic and linear SOA terms perform better than any of the standard regression models. This is to be expected since the U-shape of type-B functions is better captured by a quadratic term than a linear term. The key aspect of this analysis was to determine whether models with interaction terms would perform better than those without interaction terms. The model M16 was the best model for each and every observer who participated in the present study. This model consists of linear SOA and set size terms as well as a quadratic SOA term but does not have any interaction term. Therefore, our analysis indicates that SOA (i.e., masking) and set size (i.e., attentional load) do not interact.

Modeling

Next, we examined the distribution of response errors of each observer by using the BMC technique (see Methods). Figure 3 (the leftmost column) shows BMC differences between every combination of model pairs for each observer. Among the four models tested, the GU model was the winning model for all observers; it has the highest BMC value. Averaged across observers, the BMC of the GU model was 27.2, 2.9, and 3.4 larger than the G, GUCA, and GUNN models, respectively. These differences correspond to ~6E+11-to-1, ~18-to-1, and ~30-to-1 odds, all favoring the GU model. According to Jeffreys’ scale of interpretation (Jeffreys, 1998), these odds correspond to “decisive evidence” favoring the GU model. Therefore, further analyses were done on model parameters of the GU model.

Fig. 3
figure 3

The first column from left represents the Bayesian Model Comparison (BMC) differences between every combination of model pairs. In order to have the same color notation (i.e., cooler colors mean better model performance and hotter colors mean worse model performance) as in Fig. 2, we flipped the sign of BMC differences. The Gaussian + Uniform (GU) model outperforms all others for all observers. The second and third columns show the parameters of the winning GU model. The second column shows the standard deviation of the Gaussian in the GU model as a function of stimulus onset asynchrony (SOA), and the third column shows the weight of the Uniform component in the GU model. The red lines represent set size two condition whereas the blue lines represent set size six condition. Error bars represent standard errors obtained by bootstrapping (see Methods). The fourth and fifth columns show Bayesian Information Criterion (BIC) differences between pairs of regression models listed in Table 2 for standard deviation of the Gaussian and the weight of the Uniform in the GU model, respectively. All color conventions are the same as in Fig. 2

Full size image

Figure 3 also shows the model parameters for the winning GU model for all observers (the second and third columns). There is no discernable pattern that is consistent across all observers in the dependence of standard deviations on SOA and set-size (Fig. 3, the second column). On the other hand, the weight of the uniform component has clear and consistent pattern in all observers (Fig. 3, the third column). The weight parameter changes as a function of SOA following an inverse-U function, which reflects the shape of Type-B metacontrast functions. These inverse-U functions appear to be shifted vertically as a function of set-size, mirroring attentional affects found in the transformed performance data. In order to quantify these informal observations, we fitted a series of regression models listed in Table 2 (see Methods for details).

Pairwise comparison results of all regression models are given in the two rightmost columns of Fig. 3. For the standard deviation parameters, the model M21 (with the following factors: SOA, SOA2, set size, SOA × set size, and SOA2 × set size) outperformed all other regression models (21st rows in each panel in the fourth column of Fig. 3) for observers CBK, FG, and SA. For observers AK, EK, and GQ, models M1, M4, and M2 were the best ones, respectively. However, almost all BIC differences were within the range of [−2, 2], suggesting that the differences between the models were not significant and all models performed equally well (or equally poorly). For observer MNA, the model M8 appeared to be the best of all, suggesting significant roles for SOA and set size as well as their first order interaction. In sum, these findings support the aforementioned informal observations that there is no clear or consistent trend across observers in the dependence of the standard deviation parameter on SOA and set-size. In our previous work (Agaoglu et al., 2015), we found that both the standard deviation of the Gaussian and the weight of the uniform distribution in the GU model correlated with the metacontrast function. The correlation of the weight parameter was higher than the correlation of the standard deviation. In the current study, the best regression model for the standard deviation had a main factor of SOA in five out of seven observers, which suggests a significant role for standard deviation of the Gaussian term in explaining metacontrast masking, consistent with the previous finding. However, this dependence did not show a consistent pattern across observers and hence may be related to individual observer-dependent variations. On the other hand, as we mentioned above and discuss below in more details, the weight parameter appears to reflect a more general property that is common across all observers.

The weight of the uniform component in the GU model showed an inverse U-shaped pattern which was consistent across observers. In three (AK, MNA, and SA) of seven observers, M16 performed best, indicating no interaction between SOA and set size. Interestingly, in the remaining four observers (CBK, EK, FG, and GQ), the best regression model was either M19 or M21, both of which have interaction term(s). The interaction between quadratic SOA term and set size is most apparent in observer CBK (the second row and third column in Fig. 3). However, for observers EK, FG, and GQ, even though the best regression model is M21, the model M16, which does not have any interaction terms, performs equally well according Jeffrey’s scale of interpretation. In fact, regressions of the weight of uniform based on adjusted R2 metric revealed that M16 is the best regression model for all observers but CBK and EK. Besides, qualitatively, interaction between SOA and set size is not very apparent for these observers. Therefore, we conclude that, although there is some evidence for interactions between masking and attention when the analysis is carried out through the weight of the uniform distribution in the GU model, the evidence for this interaction is neither consistent across observers, nor strong. Hence, in the light of the analysis carried out directly on transformed performance, we conclude that attention and metacontrast masking do not interact. Table 4 summarizes the best regression models in capturing the change in model parameters as a function SOA and set size, for each observer.

Table 4 The winning regression model for each parameter and observer
Full size table

Another way to understand how model parameters and masking functions are related is to compute the correlation between each model parameter and masking functions. Figure 4 shows individual correlation coefficients as well as the average across observers. The weight of the Uniform in the GU model strongly correlates with masking functions, and set size does not change the strength of this correlation (one sample t-tests, p < 0.0001; Bayes factor > 7×105, in favor of strong correlation). Interestingly, the standard deviation of the Gaussian in the GU model correlates with masking function in set size two condition (one sample t-test: t6=-2.50, p=0.046; Bayes factor (correlation/no correlation) = 2.01) but this correlation vanishes in set size six condition (one sample t-test: t6=−0.67, p=0.53; Bayes factor = 0.42.) We will discuss these findings in the next section.

Fig. 4
figure 4

The correlation between model parameters and masking functions for each set size condition. The correlation coefficients for individual observers as well as average across observers are shown. The red and blue bars represent set size two and six conditions, respectively

Full size image

Discussion

The visual system constantly receives an overwhelming amount of information. Due to capacity limitations, it becomes necessary to select and/or enhance relevant information while suppressing irrelevant information for the task at hand. These attentional effects can be quantified experimentally with tasks that require the observer to detect, discriminate, or recognize a given object. In spatial cueing paradigms, attentional resources are directed to specific spatial locations and performance at cued and uncued locations are compared. In visual search paradigms, the “attentional load” is manipulated by means of different number of distractor objects/features (see review Carrasco 2011 for a detailed taxonomy of attentional effects). Visual masking has also been shown to control the quantity and quality of information transfer from sensory memory to short-term memory. An intuitive question is whether these two processes that control the transfer of information from sensory memory to short-term memory operate independently or interact.

In this study, we asked observers to report the orientation of a target bar randomly selected from a set of bars presented in the display. Since the target bar was indicated by a metacontrast mask or a peripheral post-cue, we assumed that by increasing the set size, observers spread their attention to more locations thereby reducing attentional benefits at individual locations. We found strong evidence against interactions between metacontrast masking and attentional mechanisms. Our results showed that mean absolute response-errors in orientation judgments are independently influenced by masking strength (a function of SOA) and attentional load (a function of set size).

Three issues need to be addressed in considering the generality of our results. First, to avoid ceiling/floor artifacts, we adjusted target and mask luminance (contrast) values individually for each observer. Given this, we cannot rule out masking-attention interactions with stimuli with very high or very low luminance (contrast) values. Second, Maksimov and colleagues have shown genetically-based individual variations in metacontrast masking (Maksimov, et al., 2013). Since we have not genotyped our subjects, we cannot generalize our results across all genotypes. Finally, our set-size/post-cue approach is only one of multiple techniques to control the allocation of attention. A priori, it is not clear whether our results would hold for other manipulations. To address this issue, in a separate study, we investigated the attention-metacontrast relationship by presenting either central or peripheral pre-cues in different blocks (Agaoglu, Breitmeyer, Ogmen, in preparation; Ogmen, Agaoglu, Breitmeyer, 2016). We kept set-size fixed and varied the time delay between the cue onset and the target onset, as well as the SOA between the target and mask arrays. We again made sure that the ceiling/floor artifacts are avoided by adjusting stimulus parameters as in this study. Our results are in agreement with the results of this study, i.e., metacontrast masking interacts neither with endogenous nor with exogenous attention (Agaoglu, Breitmeyer, & Ogmen, in preparation; Ogmen, Agaoglu, Breitmeyer, 2016).

As mentioned in the Introduction section, while some models of masking view attention as an integral component of masking effects, others view it as an independent add-on process. In particular, the object-substitution model of masking, which was derived from the common-onset masking experimental paradigm, posited interactions between masking and attention and provided empirical evidence in support of this prediction. Other studies provided empirical evidence for masking-attention interactions in metacontrast masking (Ramachandran & Cobb, 1995; Shelley-Tremblay & Mack, 1999; Tata, 2002), raising the possibility that these interactions could be an essential component of all masking types. However, recent studies, using the common-onset masking paradigm, showed that the interaction between masking and attention was an artifact of ceiling/floor effects and provided evidence against the prediction of the object substitution model (Argyropoulos et al., 2013; Filmer et al., 2014, 2015; Pilling et al., 2014). A goal of our study was to examine whether the interaction between attention and masking in metacontrast could also be a result of floor/ceiling effects. By avoiding floor/ceiling effects, we showed strong evidence against masking and attention interactions in metacontrast masking. In the light of this finding, we now discuss previous studies that reported interactions between these two processes.

Ramachandran and Cobb (1995) used a row of three disks (central one being the target) and a column of four flanking disks (two above and two below the target disk). They asked observers to give a visibility rating for the target disk on a scale of 0 to 5. They found stronger masking when observers attended the column of disks which constituted the mask compared to when they attended the row of disks that included the target. The authors interpreted this finding as an interaction between attention and backward masking. However, it is very likely that the interaction reported by Ramachandran and Cobb was a result of a ceiling effect: When observers attended the row of disks containing the target, visibility ratings were high, and for some SOA values, were very close to 5 (the maximum value).

Tata (2002) reported similar findings and interpretations with metacontrast masking. He used elements similar to Landolt Cs and asked observers to report the orientation of the masked one. He varied set-size to control the attentional load and found significant interactions between set-size and masking. However, as in Ramachandran and Cobb’s study, performances in Tata’s experiments also suffered from ceiling effects: For short and long SOAs (e.g., 0 ms and 240 ms), discrimination performance in all set-size conditions was in the range of 90–95 % correct whereas at intermediate SOA values, performance dropped significantly and diverged. The ceiling effect was rather more obvious in this study because with a set-size of one, there was essentially no masking at all (performance as a function of SOA formed a flat line at about 95 % correct), whereas at set-size of eight, there was strong masking with a typical type-B masking function.

Another study that investigated metacontrast masking and attention also showed significant interactions (Shelley-Tremblay & Mack, 1999). In inattentional blindness studies, meaningful stimuli were found to be more resistant to inattentional blindness than neutral stimuli. This was interpreted as meaningful stimuli automatically attracting additional attentional resources compared to neutral stimuli. Following this logic, Shelley-Tremblay and Mack (1999) manipulated attention by using meaningful (happy-face icon, individual name) versus neutral stimuli (inverted face icon, scrambled face icon, neutral words, annulus). They found that targets consisting of happy-faces and one’s own name were more resistant to masking than scrambled variants of them (facial features within a happy-face icon or letters in one’s name were randomly located) and meaningful stimuli used as masks exerted stronger masking effects than neutral masks. More importantly, their data indicated significant interactions between target/mask manipulations and SOA. The interpretation of these data in favor of interactions is subject to two important caveats: First, baseline performance for each type of stimulus (i.e., without a mask) was not measured; therefore one cannot judge the strength of masking and/or the presence of a ceiling effect. Second, in the experimental design, target or mask type covaries with attentional manipulation. This is especially important given that changes in the target or mask type, not only in terms of low-level parameters (e.g., luminance), but also in terms of higher-level organization, are known to affect metacontrast masking functions (e.g., Dombrowe, Hermens, Francis, & Herzog, 2009; Sayim, Manassi, & Herzog, 2014; Williams & Weisstein, 1981). For example, in two studies (A. Williams & Weisstein, 1978; M. C. Williams & Weisstein, 1981), target and mask configurations are manipulated in terms of their three-dimensional appearance and connectedness. Both of these factors affected metacontrast functions; connectedness influencing mainly the strength of masking and depth influencing mainly the timing of masking. Similar types of influences would be expected in the case of Shelley-Tremblay’s and Mack ‘s stimuli: Given the cognitive significance of happy faces and one’s own name, it is likely that they are processed faster than neutral stimuli, suggesting shifts in the timing of metacontrast, hence interaction effects. In summary, because the target or the mask type covaried with the attentional manipulation, it is not clear whether the interaction found in Shelley-Tremblay and Mack (1999) is due to target and mask types based on figural, Gestalt, or “object superiority” effects, or to attention itself.

Effects of attention and masking on signal and noise

Although attentional effects are very well established with various visual tasks, there is no consensus about its mechanistic basis. Based on psychophysical, neurophysiological, and neuroimaging data, many computational models of attention have been proposed. Proposals include signal enhancement, external noise reduction, distractor exclusion, change in decision criteria and/or spatial uncertainty, normalization of pre-attentive activity by attention/suppression fields, increase in information transfer to VSTM, accelerating information processing, sharpening of tuning curves, modulating contrast and/or response gains, and many more (e.g., Carrasco & McElree, 2001; Carrasco, Penpeci-Talgar, & Eckstein, 2000; Carrasco, 2011; Desimone & Duncan, 1995; Dosher & Lu, 2000a, 2000b; Eckstein, 1998; Herrmann, Montaser-Kouhsari, Carrasco, & Heeger, 2010; Lee, Itti, Koch, & Braun, 1999; Lu & Dosher, 1998; Palmer, 1994; Pestilli, Ling, & Carrasco, 2009; Reynolds & Heeger, 2009; Smith, Ellis, Sewell, & Wolfgang, 2010; Smith, Lee, Wolfgang, & Ratcliff, 2009; Smith & Ratcliff, 2009). These processes are not mutually exclusive and can work in parallel with different contributions in different stimulus/task conditions. For instance, in precuing of location, the effects of cue-validity can be explained primarily by external noise reduction when there is high amount of noise in the stimuli whereas signal enhancement accounts for attentional effects in low external noise conditions (Dosher & Lu, 2000a; Lu & Dosher, 1998). Modulating contrast and response gains have been associated with endogenous (i.e., central cueing) and exogenous (i.e., peripheral cueing) attention, respectively (Herrmann et al., 2010; Pestilli et al., 2009). What do our results imply in terms of signal and noise modulation by attention and masking? Our data suggest that masking reduces the target signal-to-noise ratio (SNR) whereas decreasing attentional load increases it and their effects simply add up. A simple interpretation of our results is that the metacontrast mask reduces the strength of the target signal thereby reducing SNR whereas attention enhances signal strength, given that our target is presented under low noise conditions. Given the lack of interactions between metacontrast and attention, these signal enhancement and reduction modulations by masking and attention take place as independent additive effects.

Implications for models of attention

Lu and Dosher developed a theoretical and experimental framework to investigate potential mechanisms of attention (Lu & Dosher, 1998). According to this framework, three distinct mechanisms of attention can be differentiated experimentally by adding varying levels of noise to the visual stimuli. The Perceptual Template Model (PTM) consists of four stages and incorporates both additive and multiplicative noise sources. The first stage is a “perceptual template,” modeled as a filter tuned to the signal. This stage filters out some of the external noise that accompanies the desired signal. In the second stage, the output of the first stage is rectified and fed into a multiplicative Gaussian noise source with zero mean and a standard deviation proportional to the signal strength (i.e., its total energy). In the third stage, an independent Gaussian noise with zero mean and a constant standard deviation is added. The last stage is a standard signal detection (i.e., decision) process that is appropriate to the task and the stimuli.

PTM can differentiate three distinct attention mechanisms each of which leads to a signature behavioral improvement in perceptual tasks. These mechanisms are (i) stimulus enhancement, (ii) external noise exclusion, and (iii) multiplicative noise reduction. There are both physiological and behavioral evidence in support of these mechanisms. For instance, at the neurophysiological level, attention has been shown to increase cellular response sensitivity (Reynolds & Chelazzi, 2004; Reynolds, Pasternak, & Desimone, 2000), to sharpen tuning curves of orientation and spatial frequency selective cells (Haenny, Maunsell, & Schiller, 1988), and to shrink neuronal receptive fields thereby excluding unwanted information through intra- or inter-layer interactions (Desimone & Duncan, 1995). At the behavioral level, attention has been associated with reduction in decision uncertainty (Palmer, Ames, & Lindsey, 1993), enhancement of the attended stimuli (Lu & Dosher, 1998; Lu, Liu, & Dosher, 2000; Posner, Nissen, & Ogden, 1978), exclusion of external noise or distractors (Dosher & Lu, 2000a, 2000b; Lu & Dosher, 2000; Lu, Lesmes, & Dosher, 2002; Shiu & Pashler, 1994), and modulation of contrast-gain (Lee et al., 1999).

There are two broad categories of spatial cueing, namely central and peripheral cueing. Central cues are generally presented at the locus of fixation and signal the location of the target stimulus in a way that requires interpretation. For example, when an arrow is used, the observer has to interpret the direction of the arrow to infer the cued location. Central cueing activates voluntary, or endogenous, attention mechanisms. Peripheral cues are generally presented at or close to the spatial location of the stimulus and hence they indicate the location of the stimulus directly in spatial representations without necessitating interpretive processes. These cues activate the reflexive, or exogenous, attention mechanisms. Lu and Dosher (2000) found that endogenous attention works by external noise exclusion whereas exogenous attention invokes both external noise exclusion and signal enhancement mechanisms.

We will consider whether PTM can explain our findings. In our experiment, we have manipulated set-size to control attention. Increased set-size can potentially affect both endogenous and exogenous attention. PTM predicts that external-noise reduction is the mechanism underlying endogenous attention effects whereas both external-noise reduction and signal enhancement underlie exogenous attention effects. Under the external-noise reduction scenario, PTM predicts large attentional effects when external noise is large. If the mask’s effect is to add noise to the stimulus, then more noise should have been added when masking is strong (e.g., Lu, Jeon, & Dosher, 2004). Accordingly, the effect of attention should be strong when masking is strong, and weak when masking is weak. Therefore, there should be interactions between attention and masking. This does not agree with our results. According to PTM, signal enhancement is most effective when external noise is low. If the mask’s effect is to add noise to the stimulus, then the attentional effect should be strongest when masking is weak and vice versa, predicting interactions between attention and masking. This does not agree with our results.

Several studies reported that cuing improves sensitivity in simple detection tasks when stimuli are presented with masks but not when stimuli are presented in the absence of masks (e.g., Lu & Dosher, 1998, 2000; Lu et al., 2002; Smith & Wolfgang, 2004, 2007). Smith and colleagues developed the integrated system model (ISM) to explain these findings (Smith & Wolfgang, 2004 – early version, no explicit VSTM layer; Smith & Ratcliff, 2009 – VSTM stage is added; Smith et al., 2010 – final version). The main assumption of the model is that attention affects the rate of information transfer from sensory memory to VSTM (Carrasco & McElree, 2001) . Crucially, ISM incorporates interacting masking and attention mechanisms and predicts larger attentional benefits when a stimulus is masked compared to when it is unmasked. Likewise, the stronger the masking is, the larger the attentional effects will be. Hence, both the aforementioned empirical findings and the predictions of ISM appear to be at odds with our findings: Our baseline data, which correspond to no mask conditions, show clear effects of attention and we found no interactions between attention and masking. However, it is important to point out that the experimental paradigms leading to different results are fundamentally different: Lack of attentional effects for unmasked stimuli were found for simple detection tasks (or equivalently for easy discrimination tasks, such as horizontal vs. vertical) that are mainly limited by luminance contrast, rather than by the similarity of stimulus alternatives. This is clearly not the case in our study, wherein observers are required to report as accurately as possible the orientation of the target line. Hence, we found the classical set-size effect in our no-mask baseline conditions, in agreement with other studies ( e.g., Palmer, 1994). It is well known that the magnocellular pathway and its associated transient mechanisms have very different contrast responses compared to parvocellular pathway and its associated sustained mechanisms (Croner & Kaplan, 1995; Kaplan & Shapley, 1986). Simple detection and easy discrimination tasks can be carried out by both transient and sustained mechanisms, whereas difficult fine-discrimination tasks are likely to necessitate sustained mechanisms. Hence, both task difficulty and the contrast level are expected to influence the mechanistic criterion contents, i.e., which mechanisms, sustained or transient, will contribute to performance. Given that attention is also known to influence transient and sustained mechanisms in different ways, the interaction effects that emerge from data may be due to changes in criterion contents. In fact, this is a major challenge for any study, including ours, seeking to analyze interactions of masking with other processes. Masking is not a unitary phenomenon and different criterion contents can lead to drastically different masking functions (Bachmann, 1994; Breitmeyer & Ogmen, 2006). In order to mitigate this issue, in this study we sought to analyze interactions based on a complete type-B metacontrast function comparing identical masking conditions (i.e., identical SOAs) while modulating attention via set-size.

There is an ongoing conflict regarding the relationship between attention and consciousness (e.g., Bachmann, 2011; Koch & Tsuchiya, 2007). Attention has been proposed as a gateway or mechanism of consciousness (Posner, 1994). This can be interpreted in two ways: (i) Attention selects and amplifies the contents of consciousness, or (ii) attention itself gives rise to consciousness (Breitmeyer, 2014). According to the first view, attention and masking operate independently because whether and how masking controls the contents of consciousness is not affected by attention. Attention can modulate only whatever is already registered into consciousness. However, the second view suggests that attention and masking operate at the same stage, and hence, their effects may interact. There are theoretical and empirical evidence for both views (e.g., Koivisto, Kainulainen, & Revonsuo, 2009; Mack & Rock, 1998; Simons, 2007). Our study gives support to the first view by providing evidence that attention and masking operate independently.

To summarize, masking and attention are both involved in information processing and transfer at multiple stages of visual processing. Determining their relationships can help us reach a richer and more integrated understanding of visual information processing. Previous studies showed significant interactions between different types of masking and attention (e.g., Di Lollo et al., 2000; Ramachandran & Cobb, 1995; Tata, 2002). However, in most of these studies, the findings suffered from methodological artifacts and/or could be interpreted by alternative accounts (rather than artefactual mask-attention interaction). Here, we investigated the relationship between metacontrast masking and attention based on two performance measures: (i) mean absolute response-errors (empirical), and (ii) distribution of signed response-errors (modeling). We found strong evidence against interactions between attention and metacontrast masking for both performance measures. As mentioned above, neither masking nor attention is a unitary phenomenon, and hence additional studies are needed to establish firmly the relations between types of masking and attention.