Abstract
Extremal edges (EEs) are borders consisting of luminance gradients along the projected edge of a partly self-occluding curved surface (e.g., a cylinder), with equiluminant contours (ELCs) that run approximately parallel to that edge. Gradient cuts (GCs) are similar luminance gradients with ELCs that intersect (are “cut” by) an edge that could be due to occlusion. EEs are strongly biased toward being seen as closer/figural surfaces (Palmer & Ghose, Psychological Science, 19(1), 77-83, 2008). Do GCs produce a complementary bias toward being seen as ground? Experiment 1 shows that, with EEs on the opposite side, GCs produce a ground bias that increases with increasing ELC angles between ELCs and the shared edge. Experiment 2 shows that, with flat surfaces on the opposite side, GCs do not produce a ground bias, suggesting that more than one factor may be operating. We suggest that two partially dissociable factors may operate for curved surfaces—ELC angle and 3-D surface convexity—that reinforce each other in the figural cues of EEs but compete with each other in GCs. Moreover, this figural bias is modulated by the presence of EEs and GCs, as specified by the ELC angle between ELCs and the shared contour.
Similar content being viewed by others
Edges in a projected image that arise from partial occlusion of surfaces provide important information about the object boundaries and relative depth relations between the two adjacent regions. The occluding surface appears closer to the viewer than the occluded surface and “owns” the edge, whereas the occluded surface is farther from the viewer and extends behind the edge (e.g., Nakayama, Shimojo, & Silverman, 1989). Accurate interpretation of occlusion edges is therefore crucial in both human and computer vision. The central question is how an edge interpretation algorithm can determine which adjacent region is the projection of the closer, occluding surface and which is that of the farther, occluded surface.
A version of this problem was first identified and studied by Gestalt psychologists nearly a century ago as the phenomenon of figure–ground organization (Rubin, 1921/1958). perceiving which side of a shared contour in a flat 2-D image corresponds to the surface that is closer to the observer, and thus “owns” the edge (i.e., the “figural” side), and which side is farther away and continues behind the edge (the “ground” side). Various image-based cues that the visual system uses to infer information about relative depth across shared edges have previously been identified (see Palmer, 1999; Peterson, 2003; and Wagemans et al., 2012, for reviews). These cues to the figural side include the region that is smaller and surrounded (Rubin, 1921/1958). more symmetrical (Bahnsen, 1928). more convex (Kanizsa & Gerbino, 1976; Metzger, 1953). more familiar (Peterson & Gibson, 1991, 1994). higher in contrast with the background (O’Shea, Blackburn, & Ono, 1994), lower in the visual field (Vecera, Vogel, & Woodman, 2002). wider at the base (Hulleman & Humphreys, 2004). grouped with the edge by virtue of relevant grouping factors (Palmer & Brooks, 2008). and/or continuous with an extremal edge (Ghose & Palmer, 2010; Huggins & Zucker, 2001a, 2001b; Palmer & Ghose, 2008).
The goal of the present research was to investigate whether an additional cue, called “gradient cuts” (GCs; Huggins & Zucker, 2001a, 2001b). that is evident in images of 3-D curved surfaces is relevant to the perception of relative depth and figure–ground in human vision. In 3-D curved surfaces, GCs arise when a shading gradient ends at the shared edge due to (a) the termination of its physical surface at the edge, (b) occlusion at the shared edge by a closer surface, or (c) both (a) and (b). GCs can be considered the complement of the figural cue of “extremal edges” (EEs; Ghose & Palmer, 2010; Huggins & Zucker, 2001a, 2001b; Palmer & Ghose, 2008). but not in the sense of being a necessary characteristic of the opposite side of the same edge, as is true for the classic cues of convexity, small size, and so forth. That is, for these classic cases of complementary cues, if one side is convex, the opposite side must be concave, and if one side is smaller, the other must be larger. This clearly is not the case for EEs and GCs, because both sides of the shared edge can be EEs or both sides can be GCs. In the case of EEs and GCs, the complementarity arises at the level of the defining feature of a single side of the edge. That is, the only difference between EEs and GCs lies in the angle between the shared edge and the equiluminance contours (ELCs) of their luminance gradients: For EEs the ELCs are approximately parallel to the edge (from zero to some upper bound of Δ deg), whereas for GCs they intersect the edge at some nonzero ELC angle (greater than Δ deg). In this article, we examine EEs and GCs in terms of the implications of their commonalities (e.g., their 3-D surface convexity) and differences (e.g., the sizes of their ELC angles) for relative depth and figure–ground perception.
Until recently, nearly all research on figure–ground perception has used displays in which both regions attached to the edge are homogeneous in color and texture and therefore are perceived as flat. However, different shading and texture gradients arise in the proximal stimulus due to optical factors, even when the distal surface is homogeneous in color and texture. Once surface shading and/or texture is included, new figure–ground cues can (and do) arise that relate to perceiving figure–ground organization in surfaces that are curved in depth. Such cues include EEs and might also include GCs. When a curved surface partly occludes itself, its EE leaves an optical signature characterized by the border of a luminance gradientFootnote 1 whose ELCs are roughly parallel to the edge, as is illustrated in Fig. 1a and b (Huggins, Chen, Belhumeur, & Zucker, 2001; Huggins & Zucker, 2001a, 2001b).Footnote 2 Palmer and Ghose (2008) reported psychophysical data establishing EEs as a powerful figural cue in the absence of any other known cue. Subsequently, Ghose and Palmer (2010) reported further psychophysical evidence that when EEs are combined with other figural cues (smaller size, edge convexity, familiarity, and surroundedness), the effects of EEs were dramatically stronger. The EE on the outer side of the inner edge of a torus (or donut), for example, is easily perceived as the closer figure, even though it is highly concave and fully surrounds the visible region of the surface visible through the central hole. In complex natural scenes, figure–ground organization is processed from a combination of information about global features (e.g., region convexity) and local features (e.g., T-junctions) (Ramenahalli, Mihalas, & Niebur, 2011, 2014). Because EEs can be extracted from local spatial filters around the edge, they are more efficient for figure–ground computations than global properties. In their study with grayscale natural images, Ramenahalli et al. (2011) established that EEs are abundant, easily detectable, and carry a unique statistical signature that can be used in subsequent figure–ground organization algorithms.
Extremal edges (EEs) and gradient cuts (GCs) in figure–ground organization. (a) When opaque surfaces at different environmental distances are optically projected onto a 2-D surface, rich information is present in natural images, in the form of shading, highlight, and texture gradients that influence the perception of relative depth and border ownership (see the text for further information). (b) Enlarged image of a rectangular area in panel A, with labels for the EE and GC sides of the shared edge. (c) A pure example of an EE (left side) opposite a GC (right side) that are identical except for the orientations of the luminance gradients relative to the shared central edge
EEs arise primarily when a curved surface partly occludes itself (e.g., the yellow squash shown in the inset of Fig. 1). GCs tend to arise either when a similarly curved surface is partly occluded by another surface that is closer to the viewer (e.g., the orange squash in Fig. 1 being occluded by the yellow one) or when such a surface has been physically cut so that its surface terminates at the edge (e.g., the lip of the gray jar in Fig. 1). Figure 1c illustrates EEs and GCs in a pure, idealized form, showing an EE on the left side of the edge and a GC on the right side of the same edge that is identical except for being rotated 90° relative to the edge. As this example illustrates, the signature difference between EEs and GCs is the difference in the angle between the ELCs and the shared edge. In EEs, the ELCs are (approximately) parallel to the shared edge, so the ELC angle is (approximately) zero. In GCs, the ELCs intersect the shared edge and the ELC angle is perceptibly different from zero (90° in Fig. 1c). When the ELCs of a GC intersect the shared edge, they form what we will call “virtual T-junctions,” in which the stem of the T is along an ELC and its top is along the shared edge (see Fig. 2).Footnote 3 Although the presence versus absence of virtual T-junctions technically discriminates between EEs and GCs, there will clearly be cases in which the ELC angle is so close to zero that virtual T-junctions will not be detected, leading observers to perceive an EE in the presence of technically present virtual T-junctions (e.g., the ELC angles in the range of 2° to 4° in Fig. 3).
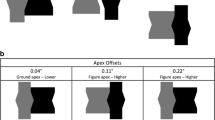
Construction and sample displays for the full-cycle and partial-cycle EE cropping conditions in Experiment 1. (a) Equiluminance contours (ELCs) are represented (in the online file) by blue dashed lines, extremal edges (EEs) by dotted red lines, and gradient cuts (GCs) by solid green lines. The ELC angle (in purple) is the acute angle between the shared edge and the equiluminance contours of the GC (farther and partly occluded) side. EEs exist at shared edges where the ELCs are parallel to the edge (i.e., the ELC angle is zero). GCs exist at shared edges where the ELCs are not parallel to the edge (i.e., the ELC angle is different from zero). The radius of curvature of the cylinder on the variable GC side (shown on the left of each image in panel b) was constant in all conditions. The EE cylinder (shown on the right in panel b) was always vertical, whereas the GC cylinder was rotated to vary the ELC angle. The value of the ELC angle was varied from 0° to 90°, as is shown in Fig. 3. A rectangular window (represented in panel a by a black-edged rectangle with a translucent orange overlay) was used to crop the region of interest so that only portions of the two cylindrical surfaces and the central edge were visible. Both left and right reversals of the display were included in the experiment. (b) Sample displays for the full-cycle EE cropping condition (left column) and the partial-cycle EE cropping condition (right column) are shown when the ELC angle was 8° (top row) and 82° (bottom row), with the variable GC side on the left
A representative set of displays in Experiment 1, in which the variable GC side was on the left for both the partial-cycle and full-cycle EE cropping conditions. The EE side (on the right) had a constant curvature with a single EE visible in the partial-cycle EE cropping condition (a) or a variable curvature with two EEs visible in the full-cycle EE cropping condition (b), as we explain in the text
Standard, explicit T-junctions arising from luminance-defined edges are known to be cues to occlusion and relative depth across an edge, with the top of the T being perceived as the edge of the closer, occluding surface, and the stem of the T belonging to the farther, occluded surface (e.g., Cavanagh, 1987; Peterson & Hochberg, 1983).Footnote 4 It therefore seems possible that the virtual T-junctions formed by the ELCs of a luminance gradient and the edge with which they intersect might also be sufficient to produce a depth-based ground bias on the GC side of an edge. If this hypothesis is true, then GCs should produce a ground bias when paired with a flat surface on the opposite side of the shared edge. However, this prediction is contrary to a claim by Huggins, Zucker, and colleagues in the computer vision literature (Huggins, Chen, Belhumeur, & Zucker, 2001; Huggins & Zucker, 2001a, 2001b) that GCs show a ground bias only when paired with EEs on the other side of the shared edge. However, their definition of “cuts” is more general and includes image edges arising from surface boundaries, surface normal discontinuities (e.g., two sides of a cube), reflectance edges, and shadows. Such a broad definition of GCs does not allow for a thorough investigation of the ground bias. In this study, we constrained the shared edge of GCs to be a depth edge and investigated figure–ground perception in GCs versus flat conditions and GCs versus EE conditions, in which GCs differ from EEs by the single feature of ELC angle.
Palmer and Ghose (2008) reported results from certain control conditions in their original EE article that contradict the hypothesis that virtual T-junctions bias the perception of ground, however. In particular, when GCs at a 90° ELC angle were paired with flat textured surfaces (see Palmer & Ghose, 2008, Fig. 2, row 2, column 3). GCs were seen as the closer figure about 65 % of the time. Although this difference was not reliably above chance (50 %), it is certainly not reliably below chance, which would be predicted on the basis of virtual T-junctions. We note that this result is consistent with the claim by Huggins, Zucker, and colleagues that GCs only bias a ground interpretation when they are opposite an EE (Huggins et al., 2001; Huggins & Zucker, 2001a, 2001b). In that case, GCs would be similar to the ground bias of “homogeneously colored regions” (Peterson & Salvagio, 2008) in being highly sensitive to context. That is, homogeneously colored regions show a ground bias in a display with multiple shared edges when the homogeneously colored regions are present on the concave side of the concave/convex boundaries, but not when the multiple concave/convex edges are replaced by straight edges.
Another way to explain the existing data, however, is to consider the possibility that two distinct factors may be at work in determining the relative depth and figure–ground perception of curved surfaces based on the EEs and GCs of luminance gradients: namely, perceptually nonzero ELC angles (or, equivalently, perceived virtual T-junctions) and 3-D surface convexity. We have already suggested why the presence of ELC angles noticeably greater than zero might serve as a potential cue to the farther ground, but that cue alone does not explain how ELC angles near 0° in EEs produce a strong cue to figure. Something else must be going on. Now suppose that this “something else” might be that 3-D surface convexity is itself a cue to figure. In this context, “3-D surface convexity” refers to the possibility that, all else being equal, a surface that “bulges” toward the observer will tend to be seen as figural and closer than an adjacent surface that is not 3-D convex. This would be consistent with ecological considerations such as the facts that many solid objects (and particularly natural ones) have convex surfaces at or near their edges and that solid objects are frequently seen against regions that people perceive as flat, such as sky, walls, floors, ceilings, and table tops. We freely admit that we know of no “ground truth” evidence that this is the case, but it seems plausible that ecological statistics, if available, would bear this out.
In the case of EEs, these two factors are mutually consistent with a figural interpretation. That is, both the cues of near-zero ELC angles and 3-D surface convexity bias the EE side of the edge toward a figural interpretation, thus producing a strong combined bias toward being seen as closer figures. GCs are more complex, however, because the figure–ground interpretations of the same two factors oppose each other for the same region and will tend to cancel. When paired with a flat region, for example, the 3-D convexity of the GC might bias it toward being perceived as a closer, figural surface, whereas its virtual T-junctions arising from large ELC angles might bias it toward being perceived as a farther, ground surface. The result thus might be no net bias, a figural bias (if 3-D convexity dominates the virtual T-junctions), or a ground bias (if the virtual T-junctions dominate the 3-D convexity). When that same GC is paired with a similarly convex EE, however, there is no difference in 3-D convexity, so the presence of virtual T-junctions due to large ELC angles will produce a bias toward ground as the ELC angle increases from 0°. These two factors—ELC angle size and the degree of 3-D convexity—must therefore be teased apart to test this two-factor account of the roles of EEs and GCs in figure–ground organization.
Lawlor et al. (2009) provided a rigorous mathematical analysis of how apparent contours interact with local shading to provide important monocular shape cues that can be used for further associations of borders with figure rather than ground in physiological boundary detection systems (e.g., Zhou et al., 2000). In the present two experiments, we provide psychophysical data on how the exterior edges of smooth convex surfaces (EEs) show primacy over the transversally cut-off shading gradient (GCs) of a similarly convex object. However, in the absence of an adjacent EE (i.e., with a flat adjacent side), the 3-D convexity of a GC shows primacy over transversally cut shading gradients for deciding border ownership.
In the first experiment, we investigated the conditions under which the EEs of smooth convex surfaces are seen as closer and figural when paired with GCs of a similarly convex surface. The second experiment showed that in the absence of an adjacent EE (i.e., with a flat adjacent side), the 3-D convexity of a GC tends to be seen as figural and closer than an adjacent flat side.
Experiment 1: GCs versus EEs—Effects of ELC angle alone
In Experiment 1 we explicitly tested the effect of the size of the ELC angle when both sides of the edge have the same 3-D convexity. Figure 2 shows the general construction of these displays, representing (in the online version) ELCs as dashed blue lines, EEs as dotted red lines, and GCs as solid green lines. One side, which we will call the “constant” (or EE) side, was always an EE at a vertical orientation, such that its ELCs were parallel to the central vertical edge and its ELC angle was 0°. It was rendered as some portion of a cylinder by means of a luminance gradient. The other side, which we will call the “variable” (or GC) side, had a luminance gradient whose ELC angle varied from 0° to 90°. The variable side was also rendered as a cylinder by a luminance gradient, but in a depth plane behind that of the constant side, such that the EE on the constant side occluded the variable side and “cut” its luminance gradient when the ELC angle was greater than 0°. (Note that when the ELC angle was 0°, the gradient on the variable side was also an EE, but we will nevertheless sometimes refer to the variable side as the “GC side” to maintain the same terminology as for other ELC angles.)
When the variable side had an ELC angle at or near 0°, the probability of seeing it as the closer figure should be about 50 %, because the constant side was also an EE with comparable 3-D convexity. Under these circumstances, the figural biases on both sides of the edge would be equal and should cancel completely, resulting in 50 % figural responses. When the variable side was a GC with an ELC angle sufficiently greater than 0°, however, the probability of seeing it as the closer figure should drop significantly below 50 % as the ELC angle increases, because the variable side would now produce virtual T-junctions in the absence of such virtual T-junctions on the constant EE side.
Method
Participants
Fifteen students with normal or corrected-to-normal vision at the University of Kaiserslautern, Germany, volunteered to participate in the experiment for payment at the rate of €6/h. All experiments were approved by the Committee for the Protection of Human Subjects at the University of Kaiserslautern, Germany. Informed consent was obtained from all participants before they began the experiment.
Apparatus
Displays were shown on a Dell UltraSharp U3014 monitor (screen size 64.1 cm × 40.1 cm) with 2,560 × 1,600 pixel resolution at a refresh rate of 60 Hz, in an otherwise dark room. Participants were positioned such that their eyes were centered on the screen and the viewing distance was 64 cm (1.42° of visual angle). The size of the images, including a homogeneous gray surround, was 484 × 384 pixels (~10.75° × 8.5°). The participant’s head was stabilized using a chin and forehead rest, and presentation and response collection were controlled by a MATLAB program (MathWorks Ltd.), using routines from the Psychophysics Toolbox (Brainard, 1997).
Design
The complete set of 60 displays was generated by a factorial combination of three factors: ELC angle, GC position, and cropping condition. In all, 15 ELC angle sizes on the GC side were sampled more finely near zero and 90° (0°, 2°, 4°, 8°, 16°, 26°, 32°, 45°, 58°, 64°, 74°, 82°, 86°, 88°, and 90°). The variable (GC) side of the display was positioned either on the left or on the right. The two cropping conditions (full-cycle and partial-cycle) arose from trade-offs in the method used to crop the cylindrical images on the EE side, as we explain below.
Stimuli
The images were created by first rendering two cylindrical luminance gradients in POVRAY, an open-source ray-tracing program (www.povray.org/). The constant EE cylinder was always vertical,Footnote 5 and the variable GC cylinder was rotated through a variable angle away from vertical (see Fig. 2a). The two gradient sides were then put together using Adobe Photoshop (www.adobe.com/photoshop), with the constant EE cylinder in the closer layer and the variable GC cylinder in the farther layer. Both layers were at 100 % opacity so that the constant EE cylinder occluded some portion of the variable GC cylinder, except at an ELC angle of 0°. The resulting composite image was then cropped using the largest rectangular window that showed nothing except the surfaces of the two cylindrical surfaces and the shared edge (Fig. 2a). Because relative size is known to be a relevant factor in figure–ground organization (Rubin, 1921/1958). the 2-D areas of the two depicted surfaces within the cropping window were equal. As a result, the cropping window size varied as a function of the ELC angle, decreasing as the ELC angle increased from 0° to 90°. The overall luminances of the two sides were also approximately the same, to control for differences in contrast with the background that also might influence figure–ground perception (Rubin, 1921/1958). The radius of curvature on the variable GC side was the same in every image.
Two different sets of images were then created that differed in the radius of curvature on the constant EE side. In the partial-cycle EE cropping condition, the radius of curvature of the EE side was also held constant, but the proportion of the EE cylinder’s full-cycle gradient that was visible necessarily varied to keep the two sides equal in area, decreasing from 100 % at 0° to 50 % at 90°. In the full-cycle EE cropping condition, the visible percentage of the EE cylinder’s luminance gradient was held constant by varying the EE cylinder’s radius of curvature so that its entire luminance gradient was visible in every display, which always showed two EEs, one along the shared edge and the other on the opposite side. The EE’s radius of curvature in the full-cycle EE cropping condition for the 90° ELC angle was approximately the same as that in the partial-cycle condition for the 90° ELC angle,Footnote 6 but it decreased systematically to 50 % of that radius as the ELC angle decreased to 0°. A representative sample of the displays in which the GC side is on the left is shown in Fig. 3. Each participant saw four replications of each display.
Procedure
Participants were instructed to indicate which side of each display appeared closer and figural on each trial by pressing the corresponding left or right arrow key. The experiment began with ten practice trials (without feedback), whose purpose was to familiarize participants with the response mapping. After the practice trials, the experimental trials were presented in a single block, during which the participants were allowed to take a break, if they wished, after any response. Each trial began with a large fixation cross in the center of a random noise field measuring 310 × 310 pixels, all surrounded by a 50 % gray background. The observer started the presentation of the next display with a key press when he or she was ready. The shared border between the two regions was on the central vertical axis of the fixation point. Each display was presented for 2 s, at which time the display was replaced with a large question mark in the center of another 310 × 310 pixel random noise field, which stayed on until the participant had responded. The participants had enough time to move their eyes and explore the full display before deciding on the figure–ground judgment. As soon as a response was made, the random noise field containing the large fixation cross was presented on a 50 % gray background to indicate the start of the next trial.
Results and discussion
The percentages of trials on which participants chose the variable GC side as closer are plotted in Fig. 4 as a function of ELC angle, averaged over the four replications, left/right position of the variable GC side, and the full-cycle versus partial-cycle EE cropping conditions. We found no reliable main effect of the left/right position of the GC side [F(1, 14) = 0.26, p = .61, η p 2 = .02], cropping condition [F(1, 14) = 1.31, p = .27, η p 2 = .08], or their interaction [F(1, 14) = 1.25, p = .28, η p 2 = .08]. There was a main effect of ELC angle [F(14, 196) = 14.25, p < .0001, η p 2 = .5], but no significant interaction between ELC angle and cropping condition [F(14, 196) = 1.03, p = .43, η p 2 = .07]. When the ELC angle was 0°, the shared edge was an EE for the luminance gradients on both sides, and the probability of selecting either side as closer was not different from chance (50 %). The EE side was first reliably seen as nearer than the GC side when the ELC angle was 4°. [For ELC angles from 4° to 90°, all ts(14) > 3.0, and all ps < .01]. As the ELC angle increased from 0°, the percentage of times that the GC side was chosen as figural diminished monotonically and asymptoted near 10 %, indicating a strong bias toward seeing the variable GC side as the farther ground with increasing ELC angle.
Results of Experiment 1: Percentages of trials on which the variable GC side (on the left in the examples shown below the graph for ELC angles of 0°, 26°, and 90°) was chosen as figural/closer as a function of the ELC angle. Error bars correspond to standard errors of the means. Figural/closer responses decrease exponentially (dark circles on curve, y = 43.574e –0.042x; R 2 = .9532) as ELC angle increases from 0 to 26°. Beyond 26°, figural/closer responses decrease about linearly with ELC angle (light squares on line, y = –0.0639x + 16.761; R 2 = .724), and the maximum value is never greater than 15 %. The data show the strong ground bias for large ELC angles when a GC region shares an edge with an EE region
The initial steep decrease in seeing the variable GC side as figural and closer is consistent with the possibility that people detect the virtual T-junctions as the ELC angle increases from zero. It is difficult to specify some particular ELC angle at which this occurs because the decline is relatively smooth, but the decrease in figural responses to the variable GC side is approximately exponential until about 26°, at which point it declines more slowly and about linearly with further increases in ELC angle. This pattern of results is generally consistent with the hypothesis that people tend to perceive the GC side as farther away and ground when its ELC angle is sufficiently greater than zero.
The present results clearly indicate that the ELCs of the shading gradients of a cylinder do not have to be exactly parallel to the shared edge to be interpreted as EEs. Indeed, the probability of seeing the gradient region as figural is quite high up to ELC angles of about 4°, and then drops steeply until about 26°, at which point it appears to level off, decreasing slowly to around 10 % figural responses. This broad range of ELC angles may result from the effects of EE gradients that are generated by other curved surfaces, such as cones and spheres, for which the ELC angles are not 0°. Generally speaking, the ELC angles of such curved surfaces on the EE side can be very close to 0° when the ELC is close to the edge, but they can deviate considerably from 0° as the ELC becomes more distant from the edge. Perhaps this is part of the reason why the decrease in figural responses is not steeper and does not asymptote at 0 % figural responses.
Experiment 2: GCs versus flat regions—Joint effects of ELC angle and 3-D convexity
Experiment 1 showed that, when the opposite side of a GC is an EE, increasing the ELC angle of the GC side relative to the shared edge dramatically decreased the probability of perceiving the GC side as closer and figural (i.e., dramatically increased the probability of perceiving the GC side as farther and ground). The most obvious interpretation of this finding is that, as the angle between the ELCs and the shared edge increases from 0° to about 26°, the resulting virtual T-junctions bias observers increasingly toward seeing the GC side as a farther surface whose ELCs have been “cut” by the closer, occluding EE.
An alternative interpretation is as follows, however.Footnote 7 When the ELC angle is 0° on the variable GC side, both sides of the common edge are EEs, so the probability of seeing one side as figural in a two-alternative forced choice paradigm is essentially at chance (50 %). Increasing the ELC angle from 0° to 90° does not bias that side toward ground, but simply weakens the figural bias of that GC side, which is maximal at 0°. As the figural bias on the variable GC side weakens at larger ELC angles, the constant EE side, which always has an ELC angle of 0°, will increasingly win the competition for figural status (e.g., Peterson & Salvagio, 2008; Peterson & Skow, 2008; Vecera, 2000). When the variable ELC angle increases beyond about 26°, the constant EE side wins 85 %–90 % of the time. In this interpretation, there is no real “ground bias” due to larger ELC angles on the variable GC side, but only a weakening of its figural bias as the ELC angle increases.
The distinction between a “bias toward ground” and a “bias away from figure” might seem to be merely semantic, but the two hypotheses actually make different predictions if the side opposite the GC is “neutral” in terms of figure–ground perception. Given current knowledge about figure–ground cues (see Wagemans et al., 2012, for a recent review). a region having no intrinsic bias toward being seen as either figure or ground should be a flat region with a straight, vertical edge whose size, shape, and contrast with the background are all perceptually equal to those properties of the region on the opposite side of the edge. If GCs produce a bias toward being perceived as a farther ground surface, then GCs with sufficiently large ELC angles should then be seen as farther grounds when they are opposite such a flat and otherwise neutral region. However, if increasing ELC angles merely weaken a figural bias for the gradient side, then GCs should produce no bias toward the perception of ground when they are opposite a flat and otherwise neutral region, even at large ELC angles. We tested these predictions in Experiment 2.
We note in advance, however, that these predictions are based on the assumption that no figure–ground cues other than the virtual T-junctions introduced by large ELC angles differentiate between the GC side and the flat side. In particular, if 3-D convexity itself is indeed a cue to figure, then the GC side will always contain an additional bias toward being seen as figure, because its luminance gradient causes it to be perceived as 3-D convex.
We examined relative depth and figural perception for simple bipartite displays in which the shared central contour was vertical and straight with a luminance gradient of variable ELC angle on the variable side and a flat surface on the constant side. The flat side was made globally equivalent in lightness to the GC side by randomizing the positions of the pixels on the variable GC side to form a globally uniform gray texture (see Fig. 5). This randomization was done separately for each ELC angle and cropping condition (see below), such that each display was fully equivalent on both sides in terms of global contrast with the background. The displays were made by creating luminance gradients of a single cylinder at different ELC angles (from 0° to 90°) in a farther layer behind the flat-textured surface with a vertical edge in the closer layer. To avoid possible confounds due to the orientations of the rectangular windows used in Experiment 1, we cropped the resulting images in the present experiment with an orientation-free circular window that precisely equated the 2-D areas of the two surfaces.
A representative set of displays in Experiment 2, in which the variable GC side is shown on the left. (a) Images in which the cropping window shows a partial cycle of the GC’s luminance gradient with a constant radius of curvature. (b) Images in which the cropping window shows a full cycle of the GC’s luminance gradient, with a radius of curvature that increases as the ELC angle increases. The left/right position of the variable GC side was counterbalanced in the actual experiment
Method
Participants
Fifteen students with normal or corrected-to-normal vision at the University of Kaiserslautern, Germany, volunteered to participate in the experiment at the rate of €6/h. Informed consent was obtained from all participants before they began the experiment itself.
Design
The complete set of 68 displays was generated by a three-way factorial design defined by the combination of 17 ELC angle sizes (0°, 1°, 2°, 4°, 8°, 16°, 26°, 32°, 45°, 58°, 64°, 74°, 82°, 86°, 88°, 89°, 90°, as is shown in Fig. 5), two cropping conditions (showing a full GC cycle or a partial GC cycle of the cylinder’s luminance gradient), and two positions of the GC side (left or right). Each participant saw every image four times in a fully within-subjects design.
Stimuli
The cylindrical luminance gradients were created in POVRAY, as described in Experiment 1. The flat, random-noise textures were created in the following way by using a Python 2.7 script. A semicircular region of radius 150 pixels was selected from the respective gradient (in the appropriate orientation). This semicircle was then duplicated and mirrored to form the other side of the display. The intensity values of each pixel of this duplicated/mirrored semicircle were randomly shuffled such that the semicircular shape was preserved (i.e., the duplicated semicircle contained the same intensity values as the original semicircle, but in different and random positions using the Python script). The original and duplicated semicircles were then combined to form a whole circle, separated by a 50 % gray line of width 1 pixel. This circle was put on a 50 % gray background using Adobe Photoshop, as described above. A representative set of displays in which the GC side is on the left is shown in Fig. 5.
Procedure
All aspects of the procedure were as described in Experiment 1.
Results and discussion
The average data are plotted in Fig. 6 for the percentages of trials on which the GC side was chosen as the closer/figural side as a function of ELC angle, averaged over the four replications, left/right reversals, and cropping conditions. We found no reliable main effects of left/right position [F(1, 14) = 0.02, p = .88, η p 2 = .00], cropping condition [F(1, 14) = 0.29, p = .11, η p 2 = .17], or their interaction [F(1, 14) = 0.47, p = .51, η p 2 = .03].
Results of Experiment 2: Percentages of trials on which the variable GC side (on the left in the examples shown below the graph, for ELC angles of 0°, 26°, and 90°) was chosen as closer and figural (vs. a contrast-controlled flat surface) as a function of the ELC angle. Error bars correspond to standard errors of the means
In most other respects, however, the present data are radically different from those obtained in Experiment 1. First, a moderate figural bias is apparent for the variable GC side at small ELC angles (0° to roughly 4°), of about 65 % figural responses (for one-tailed comparisons with the 50 % chance level, p values ranged from .03 to .06).
This increase in figural responses for the GC side at small ELC angles compared with those in Experiment 1 (see Fig. 4) is presumably due to the fact that the constant flat side in Experiment 2 had essentially no figural bias, whereas the EE side of Experiment 1 has a strong figural bias, thereby allowing the variable GC side in the present experiment to win the figure–ground competition against the flat side more often than it did against the EE side in Experiment 1. This figural bias for the GC side is consistent with the modest figural bias of 65 % reported by Palmer and Ghose (2008) when it was opposite a flat textured surface. Second, a small, but reliable, effect of ELC angle emerged in the present experiment [F(16, 224) = 2.02, p = .013, η p 2 = .13], reflecting the modest gradual decrease in figural responses as the ELC angle increased. This effect was presumably due to the strengthening of virtual T-junctions as the ELC angle increased, because that is the primary cue that varied in both Experiments 1 and 2.Footnote 8 Because the pixels on the constant flat side were simply a rearrangement of those on the variable GC side on an image-by-image basis, there were no differences in global luminance contrast with the background between the two sides as a function of ELC angle. Third, we found no reliable figural effect for large ELC angles from about 74° to 90° [all ts(14) < 0.73, all ps > .47]. The fact that figural responses were effectively 50 % in this range of large ELC angles raises the question of why there was no evidence of a ground bias here, if GCs indeed produce a bias toward being seen as farther grounds. The most obvious possibility is that the GC side may contain some additional cue to closer, figural status whose bias was offset by the increasing ELC angle and the corresponding detection of virtual T-junctions. Our present hypothesis is that the additional cue is 3-D surface convexity along the shared edge.
General discussion and conclusions
We began by asking a seemingly straightforward question: Do GCs produce a bias toward the perception of a farther ground that is essentially opposite to the bias that EEs produce toward perception of figure? Various considerations led us to the hypothesis that both GCs and EEs involve the simultaneous influences of two factors: ELC angle and 3-D surface convexity. ELC angle is the angle between the ELCs of a luminance gradient and the shared edge of their regional contour. The closer the ELC angle is to 0° on the gradient side of the edge, the stronger is the bias toward seeing the gradient side as figure, and the farther the ELC angle is from 0°, the greater is the bias toward seeing the gradient side as ground. The term “3-D convexity” refers to the perception of a surface that bulges toward (convex) or away from (concave) the observer. The more the surface bulges toward the viewer along the edge, the stronger is the bias toward seeing that side as figure. Both factors are relevant to the perception of GCs and EEs. As is shown in Fig. 2, both factors bias EEs toward being seen as figure, producing the very powerful cue to figural perception of that region, whereas the two factors bias GCs in opposite ways, leading to either a bias toward figure, a bias toward ground, or no bias, depending on the relative strengths of the ELC Angle and 3-D Curvature factors relative to the opposing region. It is perhaps for this reason that Huggins, Zucker, and colleagues (Huggins, Chen, Belhumeur, & Zucker, 2001; Huggins & Zucker, 2001a, 2001b) suggested that GCs are only cues to ground when they are opposite an EE: They are only seen as ground consistently when there is a (convex) EE on the opposite side.
The results of the present experiments support this account of EEs and GCs, albeit with a few caveats. In Experiment 1, we studied the effects of ELC angle on figure–ground perception when the constant side contained an EE and the variable side contained a gradient whose ELC angle varied from 0° to 90°. In this case, both sides had the same 3-D curvature, so the only effective variable was the ELC angle, which caused the percentage of figural responses to the variable (GC) side to decrease from 50 % at 0° to about 10 % at 90°, with the greatest decreases occurring between 0° and 26°.
In Experiment 2, we studied the effects of ELC angle on figure–ground perception when the constant side contained a flat-textured surface and the variable side contained a gradient whose ELC angle varied from 0° to 90° (i.e., under conditions identical to those of Exp. 1, except replacing the EE on the constant side with a flat surface). Here, the results differed dramatically from those in Experiment 1, producing a weak figural bias of about 65 % at 0° and decreasing slowly with ELC angle to about 50 % at 90°. In this case, the variable GC side should be biased toward figure at 0° due to its 3-D convexity along the shared edge and near-0° ELC angle, whereas the flat surface on the constant side was undefined in ELC angle and had zero 3-D convexity. As the ELC angle of the GC side increased from 0° to 90°, its ground bias should increase due to the detection of virtual T-junctions, leading to the cancellation of the 3-D convexity figural bias by 90°.
The present research implies that the interpretation of relative depth across an edge in figure–ground processing for curved surfaces is a complex problem. We have reported evidence that even for simple luminance gradients generated by a cylinder along a shared straight edge, at least two underlying factors are relevant for interpreting the depth and figural status of the adjacent regions: 3-D surface convexity and ELC angle size. Other factors are potentially relevant as well, however, including the shape of the shared edge and its relation to the luminance gradients. Figure 7 shows one example, in which the right side of both images is a homogeneous flat region and the left side is a sinusoidal luminance gradient with GCs along its right edge. The only obvious difference is the phase of the luminance grating relative to the sawtooth edge. In Fig. 7a, the darkest ELCs of the luminance gradients coincide with the concave angles of the edge (with respect to the gradient side), and in Fig. 7b the darkest ELCs coincide with the convex angles of the edge. Nevertheless, the difference in figure–ground perception is dramatic. Figure 7a looks like a series of cylindrical tubes in front of a flat uniformly gray background that extends behind them, whereas Fig. 7b looks like a series of similar cylindrical tubes extending behind a jagged gray occluding surface. This example clearly indicates that further research is required to understand the complex role of GCs in the perception of figure and ground when curved surfaces are involved.
Notes
We use the term “luminance gradient” as a general description that includes both shading gradients (e.g., the left edge of the gray jar in Fig. 1A) and highlight gradients (e.g., the right edge of the gray jar). EEs and GCs in texture gradients are also possible, if one simply replaces ELCs with equidensity contours in the definitions and descriptions given here, though we have not used texture gradients in the research reported here.
In the computer vision literature, EEs have sometimes been called “folds,” following the naming convention in topology (e.g., Huggins & Zucker, 2001a, 2001b). This label seems to apply more naturally to situations in which gradient patterns define a depth edge between different regions of the same surface, such as folds of cloth in curtains or a full skirt. In discussing figure–ground issues, we prefer the EE terminology employed by Barrow and Tennenbaum (1978), because it applies to cases in which the edge in question marks the bounding contour of the object on one side. Nevertheless, we acknowledge that what we mean by “EEs” is the same as what Zucker and colleagues (Huggins et al., 2001; Huggins & Zucker, 2001a, 2001b) mean by “folds,” and that contours with the gradient structure of EEs do not always correspond to object boundaries.
We call them “virtual T-junctions” because the ELCs of a luminance gradient are not “real” contours, but ones that are inferred by computing image-based properties of the luminance structure of the gradient.
Subsequent research by Gillam and Grove (2011) demonstrated that T-junctions are more effective as cues to ground when they have higher entropy.
The 90° ELC angle stimuli in the full-cycle and partial-cycle conditions were not exactly the same. The partial-cycle stimuli were cropped slightly more than the full-cycle stimuli to ensure the presence of one or two EEs in the image, respectively.
We thank an anonymous reviewer for suggesting this interpretation of Experiment 1’s results.
We note that the relevant factor may turn out to be better described in some other terms, such as some ratio of the power in different orientation channels or the level of activation in certain classes of end-stopped cells in visual cortex. Here we have described it in terms of virtual T-junctions because of their connection with the ecological condition of partial occlusion that often causes GCs and because of the analogy with the role of standard, explicit T-junctions in depth perception. As we discuss them, virtual T-junctions are identified with ELC angles perceptibly greater than zero.
References
Bahnsen, P. (1928). Eine Untersuchung über Symmetrie und Asymmetrie bei visuellen Wahrnehmungen. Zeitschrift für Psychologie, 108, 129–154.
Barrow, H. G., & Tennenbaum, J. M. (1978). Recovering intrinsic scene characteristics from images. In A. Hanson & E. Riseman (Eds.), Computer vision systems (pp. 3–26). New York: Academic Press.
Brainard, D. H. (1997). The psychophysics toolbox. Spatial Vision, 10, 433–436. doi:10.1163/156856897X00357
Cavanagh, P. (1987). Reconstructing the third dimension: Interactions between color, texture, motion, binocular disparity, and shape. Computer Vision, Graphics, and Image Processing, 37(2), 171–195.
Ghose, T., & Palmer, S. E. (2010). Extremal edges versus other principles of figure–ground organization. Journal of Vision, 10(8), 3:1–17.
Gillam, B. J., & Grove, P. M. (2011). Contour entropy: A new determinant of perceiving ground or a hole. Journal of Experimental Psychology: Human Perception and Performance, 37, 750–757. doi:10.1037/a0021920
Huggins, P. S., Chen, H. F., Belhumeur, P. N., & Zucker, S. W. (2001). Finding folds: On the appearance and identification of occlusion. In Proceedings of Computer Vision and Pattern Recognition (CVPR ’01) (Vol. 2, p. 718). Los Alamitos, CA: IEEE Press.
Huggins, P. S., & Zucker, S. W. (2001a). Folds and cuts: How shading flows into edges. In Proceedings of eighth international conference of computer vision (pp. 153–158). Los Alamitos, CA: IEEE Press.
Huggins, P. S., & Zucker, S. W. (2001b). How folds cut a scene. In C. Arcelli, L. Cordella, & G. Sanniti di Baja (Eds.), Proceedings of the fourth international workshop on visual form (pp. 323–332). New York, NY: Springer.
Hulleman, J., & Humphreys, G. W. (2004). A new cue to figure–ground coding: Top-bottom polarity. Vision Research, 44, 2779–2791.
Kanizsa, G., & Gerbino, W. (1976). Convexity and symmetry in figure–ground organization. In M. Henle (Ed.), Vision and artifact (pp. 25–32). New York: Springer.
Lawlor, M., Holtmann-Rice, D., Huggins, P., Ben-Shahar, O., & Zucker, S. W. (2009). Boundaries, shading, and border ownership: A cusp at their interaction. Journal of Physiology, 103, 18–36.
Metzger, W. (1953). Gesetze des Sehens [Laws of seeing]. Frankfurt, Germany: Waldemar Kramer.
Nakayama, K., Shimojo, S., & Silverman, G. H. (1989). Stereoscopic depth: Its relation to image segmentation, grouping, and the recognition of occluded objects. Perception, 18, 55–68.
O’Shea, R. P., Blackburn, S. G., & Ono, H. (1994). Contrast as a depth cue. Vision Research, 34, 1595–1604.
Palmer, S. E. (1999). Vision science: Photons to phenomenology. Cambridge, MA: MIT Press.
Palmer, S. E., & Brooks, J. L. (2008). Edge-region grouping in figure–ground organization and depth perception. Journal of Experimental Psychology: Human Perception and Performance, 34, 1353–1371. doi:10.1037/a0012729
Palmer, S. E., & Ghose, T. (2008). Extremal edge a powerful cue to depth perception and figure–ground organization. Psychological Science, 19, 77–83.
Peterson, M. A. (2003). On figures, grounds, and varieties of surface completion. In R. Kimchi, M. Behrman, & C. Olson (Eds.), Perceptual organization in vision: Behavioral and neural perspectives (pp. 87–116). Hillsdale NJ: Erlbaum.
Peterson, M. A., & Gibson, B. S. (1991). The initial identification of figure–ground relationships: Contributions from shape recognition processes. Bulletin of the Psychonomic Society, 29, 199–202.
Peterson, M. A., & Gibson, B. S. (1994). Must figure–ground organization precede object recognition? An assumption in peril. Psychological Science, 5, 253–259.
Peterson, M. A., & Hochberg, J. (1983). Opposed-set measurement procedure: A quantitative analysis of the role of local cues and intention in form perception. Journal of Experimental Psychology: Human perception and performance, 9(2), 183.
Peterson, M. A., & Salvagio, E. (2008). Inhibitory competition in figure–ground perception: Context and convexity. Journal of Vision, 8(16), 4.
Peterson, M. A., & Skow, E. (2008). Inhibitory competition between shape properties in figure–ground perception. Journal of Experimental Psychology: Human Perception and Performance, 34, 251–267. doi:10.1037/0096-1523.34.2.251
Ramenahalli, S., Mihalas, S., & Niebur, E. (2011). Extremal edges: Evidence in natural images. In 45th Annual Conference on Information Sciences and Systems (CISS 2011) (pp. 1–5). Los Alamitos, CA: IEEE Press.
Ramenahalli, S., Mihalas, S., & Niebur, E. (2014). Local spectral anisotropy is a valid cue for figure–ground organization in natural scenes. Vision Research, 103, 116–126.
Rubin, E. (1958). Figure and ground. In D. C. Beardslee & M. Wertheimer (Eds.), Readings in perception (pp. 194–203). Princeton, NJ: Van Nostrand (Original work published 1921).
Vecera, S. P. (2000). Toward a biased competition account of object-based segregation and attention. Brain and Mind, 1(3), 353–384.
Vecera, S. P., Vogel, E. K., & Woodman, G. F. (2002). Lower region: A new cue for figure–ground assignment. Journal of Experimental Psychology: General, 131, 194–205. doi:10.1037/0096-3445.131.2.194
Wagemans, J., Elder, J. H., Kubovy, M., Palmer, S. E., Peterson, M. A., Singh, M., & von der Heydt, R. (2012). A century of Gestalt psychology in visual perception: I. Perceptual grouping and figure–ground organization. Psychological Bulletin, 138, 1172–1217. doi:10.1037/a0029333
Zhou, H., Friedman, H. S., & Von Der Heydt, R. (2000). Coding of border ownership in monkey visual cortex. Journal of Neuroscience, 20, 6594–6611.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ghose, T., Palmer, S.E. Gradient cuts and extremal edges in relative depth and figure–ground perception. Atten Percept Psychophys 78, 636–646 (2016). https://doi.org/10.3758/s13414-015-1030-2
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13414-015-1030-2