How often does one need to determine the depth relationships between surrounding objects with high accuracy and discriminate fine details? How often does one need to determine the metric properties of a 3-D scene? Somewhat surprisingly, such requirements are only seldom met. In many real-life situations, the observer only makes nominal or ordinal judgments of a scene’s spatial layout. When deciding how to interact in an environment on the basis of available sensory data, the observer often makes a discrete choice, such as when attempting to answer many types of questions: Should I begin running to catch the bus that has just arrived at the bus stop? Can I cross the road right now without the risk of being hit by an approaching car? Which of the available paths will get me to my destination most quickly? Could I manage to hit that fast-moving tennis ball? Will I be able to reach the peak of that mountain on the horizon before sunset? None of these spatial tasks is overly complex, and highly detailed reconstruction of depth relationships is not needed in these cases. Thus, from an evolutionary perspective, it seems plausible to assume that information about spatial relationships is determined in a quantity and quality sufficient for solving the task and that the observer’s visual system uses simple, direct strategies (e.g., Gibson & Bergman, 1954; Glennerster, Rogers, & Bradshaw, 1996; Lee, 1980). For instance, Gibson (1950) argued that much of our perceptual awareness of the environment is based on simple order relations that can be described in terms of “greater than” or “less than.” According to both Cutting and colleagues and Koenderink and colleagues, perceived depth is normally confined to a number of depth planes; only when the observer needs to know more precise information about how an object or its parts are positioned in space (such as when recognizing a face) does perceived depth become more articulated (Cutting, 1998, 2003; Cutting & Vishton, 1995; Koenderink, van Doorn, & Wagemans, 2011; van Doorn, Koenderink, & Wagemans, 2011).

Contrary to real-life experience, most research on visual space perception has required an observer to provide a metrical description in terms of Euclidean distances and angles (for exceptions, see Aznar-Casanova, Matsushima, Da Silva, & Ribeiro-Filho, 2008; Norman & Raines, 2002; Norman & Todd, 1998; Norman, Todd, Perotti, & Tittle, 1996; Todd & Reichel, 1989; Toye, 1986; van Doorn et al., 2011). Depth-probing methods have included absolute metric estimation (Bingham, 1993; Durgin & Li, 2011; Foley, Ribeiro-Filho, & Da Silva, 2004; Levin & Haber, 1993; Matsushima, de Oliveira, Ribeiro-Filho, & Da Silva, 2005; Toye, 1986; Wagner, 1985), relative metric estimation (Baird & Biersdorf, 1967; Nefs et al., 2013; Norman et al., 1996; Wagner, 1985), various adjustment procedures (Blumenfeld, 1913; Cuijpers, Kappers, & Koenderink, 2000, Cuijpers, Kappers, & Koenderink, 2002; Kelly, Loomis, & Beall, 2004; Koenderink, van Doorn, Kappers, & Lappin, 2002; van Doorn, Koenderink, & Wagemans, 2013), and determination of the point of subjective equality (Clément, Skinner, & Lathan, 2013; Kudoh, 2005; Lappin, Shelton, & Rieser, 2006; Loomis, da Silva, Fujita, & Fukusima, 1992; Loomis & Philbeck, 1999; Loomis, Philbeck, & Zahorik, 2002; Šikl & Šimeček, 2011; Todd, Oomes, Koenderink, & Kappers, 2001; Trommershäuser, Maloney, & Landy, 2003). All of these experimental tasks require the observer to make accurate metric depth estimates, and all experiments based on these tasks assume that the observer will succeed in establishing a unique, subjectively correct response. For instance, when an observer matches a 20 % larger stimulus in a matching task, this response is interpreted as indicating that his or her perception is different than it would be if he or she had matched a 25 % larger stimulus. In the blind-walking task, when an observer stops 50 cm from the destination, this response is interpreted as indicating that his or her perception is different than it would be if he or she had stopped 60 cm from the destination, and so forth. Even the smallest difference in the observer’s responses is interpreted as indicating different depth perception.

This assumption of the observer’s absolute certainty and perfect confidence in responses appears to be unwarranted. In our previous experimental study (Šikl & Šimeček, 2011), observers were asked to estimate the size and direction of a stimulus formed by two rods by positioning a third rod in the neighboring space to form an evenly spaced collinear triple of rods. We repeatedly observed that, rather than giving one and only one correct response that was perceived as being subjectively correct, the participants spontaneously arrived at a rather large range of admissible responses. As was numerously cited during the inquiry, all of the responses were subjectively equally plausible within this range, indicating that all of these admissible responses corresponded to the same perception. In fact, a task that forced the observers to find a specific place in the environment was somewhat frustrating primarily because of the need to choose between more than one “correct” response. The observers consistently reported the task to be quite difficult. Other experimental studies have also demonstrated observers’ limited confidence in their judgments (Bingham, 2005; Lappin et al., 2006), their application of undesirable cognitive corrections (Gogel & Da Silva, 1987; Matsushima et al., 2005; Richardson & Waller, 2005), and increased reaction times (Todd & Reichel, 1989) when performing Euclidean tasks.

In the experiment reported in this article, we examined whether, in addition to the mentioned indirect indicators of overly high demands on the observers, the principal measures of perceptual performance (i.e., precision and consistency) are affected in tasks that require higher orders of measurement. To answer this question, we prepared a distance perception experiment that included three phases with similar designs but different required response metrics. In the first phase, subjects performed ordinal distance judgments; in the second phase, they performed ratio distance judgments; and in the third phase, they performed absolute-magnitude distance judgments. We investigated whether with increased required depth description levels, perceptual performance would decrease accordingly. By comparing the observers’ judgments on ordinal, ratio, and absolute depth relationships, among others, we can then determine whether the considerable difference between visual space and physical space described in the literature at least partially reflects specific task demands.

Method

Observers

Two male and four female undergraduate students with no previous experience with psychophysical experiments volunteered as observers for all of the experiments reported here. Each observer completed two 1.5-h sessions on separate days; the same tasks were performed on each day, only at different scales (see below). In the first session, the observers saw the small-scale stimuli, and in the second session, the observers saw the large-scale stimuli. All participants had normal binocular vision and visual acuity.

Experimental setup

The experiment was conducted on a flat grassy field (approximately 40 × 60 m) that was surrounded by trees and buildings. The visual scene contained 11 metal posts. Each post was 20 cm tall and was identified by a number (1 through 11) written on a 10 × 10 cm white sheet of plastic affixed to the top. All posts were visible throughout the experiment. The only variable was the scale of the stimulus spatial configuration: In the large-scale configuration, all of the posts were confined to a square region in front of the observer with a side length of 12 m; in the small-scale configuration, the square had a side length of 4 m. In the large-scale configuration, the nearest post was 5.6 m away and the farthest post was 12.3 m away; in the small-scale configuration, the nearest post was 1.9 m away and the farthest post was 4.1 m away. The centers of the spatial layouts were located 8.5 and 2.8 m, respectively, from the observation point. Except for their scales, the two configurations were identical.

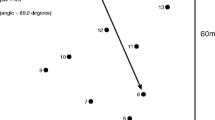
The posts were located such that (1) there were a wide range of distances between individual posts and a wide range of orientations between the intervals formed by pairs of posts, and (2) from each post, the distances to at least two other posts were approximately equal (i.e., discriminating between the individual interpost distances was a nontrivial task). The spatial configuration of the experimental posts is shown in Fig. 1.

Fig. 1
figure 1

Stimulus spatial configuration for the three phases of the experiment, viewed from above. The diamonds represent the positions of the posts, and the square indicates the boundaries of the experimental field. The two scales are indicated on the sides of the panel. The observer’s position is measured from the bottom left of the layout

Full size image

Procedure

The observers stood on a marker located at one corner of the square region and were given a package of response sheets on which they were asked to record their distance estimates. In the three phases of the experiment, the observers judged the interobject distances using the following methods: (i) by determining the distance ordering from various posts to the reference standard (ordinal distance judgments), (ii) by comparing the distance between a pair of posts with the reference unit (ratio distance judgments), and (iii) by numerically estimating the distance between a pair of posts (absolute-magnitude distance judgments). The order of the individual phases of the experiment varied between observers so that each possible ordering of the three phases was distributed equally across all observers. On the other hand, the sequence of the stimuli within each phase (see below) remained constant. Objective instructions were employed.

During the ordinal distance judgment phase, the observers estimated the interobject distances such that they ranked the posts according to the distances from the reference standard. At the beginning of the experiment, Post Number 1 was selected as the reference, and the observers were asked to indicate which of the remaining ten posts appeared closest to the reference, which was second closest, and so on. After the observers had completed their responses, Post Number 2 was selected as the reference and the experimental procedure was repeated; this process continued until all posts had been used as the reference. Using this procedure, 11 rows containing ten responses each were obtained, yielding 110 responses in total. The experiment was repeated for both scales of the stimulus spatial configuration, yielding an overall total of 220 ordinal distance judgments from each observer. The observers were given as much time as they needed to respond and received no feedback. The experiment typically took 15 min to complete for each scale.

In the ratio distance judgment phase, the observers were first asked to indicate the closest post to the reference standard (Post Number 1, to begin with). Subsequently, the observers were told to assume that the distance between these two posts was a metric unit. They were then asked to numerically estimate the distances between all of the remaining posts in the field and the reference standard. For example, if the distance between a reference and the second closest post appeared to be twice as great as the unit distance, the observers would respond 2.0. Again, as in the ordinal task, after the distances from all posts with respect to the unit distance had been compared, Post Number 2 became the reference standard. The procedure continued until all of the posts had been used as the reference. Using this procedure, 110 responses were obtained. Including both scales of the stimulus spatial configuration, 220 pairwise ratio distance judgments were collected from each observer. The observers were given as much time as they needed to respond and received no feedback. The experiment typically took 40 min for each scale.

In the absolute-magnitude distance judgment phase, the observers were required to judge the distances in centimeters between all 55 possible pairs of the 11 posts. A total of 110 absolute magnitude distance judgments were collected from each observer (55 pairs × 2 scales). The observers were given as much time as they needed to respond and received no feedback. The experiment typically took 30 min to complete for each scale.

Results

Three types of data were obtained from the three phases of the experiment, each with different levels of description of depth, and each requiring somewhat different analysis techniques. Nevertheless, observers’ performance in the individual phases of the experiment could be directly compared, because all of the data referred to the perceptual judgments of interobject distances in the same stimulus spatial configuration. To assess the precisionFootnote 1 of the observers’ judgments measured at the different scales, it was necessary to transform the data collected using ordinal, ratio, and magnitude estimations into a common format. In principle, two methods of transformation were possible. First, the data could be transformed to the weakest shared level of measurement (in this case, an ordinal scale). Such a transformation would provide information regarding the observers’ relative distance judgments. Importantly, however, the informational content of the data at the higher levels of measurement obtained in a ratio distance task and in an absolute magnitude distance task would necessarily be reduced, because the judgments would be treated nonmetrically and only ordinal information about the compared distances would enter into the analysis; the more specific information regarding the magnitude of the perceived differences would not be included. The alternative method of transformation was multidimensional scaling, which would allow metric information to be obtained regarding a perceived spatial layout and its relationship to the actual layout. This transformation, however, might result in a loss of information regarding possible data inconsistencies, in terms of minimality, symmetry, and triangle inequality (Wagner, 2006), as expressed by Kruskal’s stress function.

Ordinal scale of measurement

For the purpose of the data analysis, the distance judgments obtained in the three phases of the experiment were converted to pairwise comparisons: In the ordinal distance task, all pairs of responses from each row (i.e., from each order ranking of ten distances referring to a given reference) were extracted and analyzed separately. The position on the response sheet determined which of the two posts was perceived as being closer to the given reference and which was perceived as being farther—that is, which of two distances was perceived as being shorter. In the ratio distance task, based on the perceived ratios of the particular interobject distances relative to the unit distance, we could infer which of any two distances from the given reference was perceived as being shorter, but without specifying by how much. In the absolute-magnitude distance task, pairs of absolute-magnitude distance judgments were compared to determine which of the two distances was perceived as being shorter, again without specifying the magnitude of the difference. Using these procedures, 495 pairwise comparisons were conducted over all phases of the experiment and scales.Footnote 2 Subsequently, values of 0 or 1 were assigned to particular pairwise comparisons that corresponded to correct or incorrect responses, respectively.

We expected most pairwise comparisons to be correct, because for the majority of the interpost distances the differences were clearly visible (the distance ratios ranged from 1.00 to 5.47, with a median value of 1.53). An increased frequency of erroneous responses would, therefore, indicate the increased level of difficulty of the experimental task. Specifically, in the statistical analysis, the mean rate of erroneous responses and the error variance were calculated. The data for the small-scale and large-scale configurations that were obtained in each experimental session were analyzed separately. Table 1 shows the mean error rates of responses and the mean error variability of the responses calculated for the small-scale and large-scale stimulus configurations and for the ordinal, ratio, and magnitude judgments. The precision and consistency of the relative distance judgments decreased clearly with increased response measurement level.

Table 1 Comparison of the results from the three phases of the experiment evaluated using an ordinal scale
Full size table

A two-way analysis of variance (ANOVA) performed on the error rates confirmed that the relative distance judgments were significantly different between measurement levels, F(2, 30) = 7.23, p = .03, η p 2 = .03, with higher precision being evident in the ordinal distance judgments. Specifically, a significant difference was found in precision between the ordinal and absolute-magnitude estimations (Bonferroni, p < .01). In addition, the precisions of the observers’ judgments differed across scales, F(1, 30) = 32.90, p < .001, η p 2 = .06. The Level × Scale interaction did not attain significance, F(2, 30) = 0.23, p = .79, η p 2 = .001.

A two-way ANOVA performed on the error variances confirmed that the relative distance judgments were again significantly different between measurement levels, F(2, 2964) = 9.57, p < .001, η p 2 = .027, with greater consistency being evident in the ordinal distance judgments. Specifically, a significant difference was found in the variances between the ordinal and absolute-magnitude (Bonferroni, p < .001) and between the ratio and absolute-magnitude (Bonferroni, p = .04) estimations. Again, the consistencies of the observers’ judgments differed across scales, F(1, 2964) = 7.69, p < .01, η p 2 = .002, and the Level × Scale interaction proved nonsignificant, F(2, 2964) = 0.55, p = .58, η p 2 = .001.

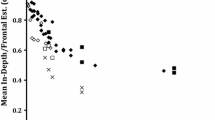
We next considered how the ordinal, ratio, and magnitude distance judgments differed when only pairwise comparisons among the stimuli oriented in mutually perpendicular directions were considered. It has commonly been observed that the in-depth dimension is perceived differently from the frontal dimension; specifically, visual space is perceptually contracted in the in-depth dimension relative to the frontal dimension, as compared with physical space (Foley et al., 2004; Kudoh, 2005; Levin & Haber, 1993; Loomis et al., 1992; Loomis & Philbeck, 1999; Norman et al., 1996; Toye, 1986; Wagner, 1985). Consequently, the in-depth distances must be made larger in order to be perceived as being equal to the frontal distances. We attempted to address the question of whether visual space shows the same degree of anisotropy, regardless of the computational demands of the different experimental tasks. To evaluate the observers’ relative distance judgments of stimuli in different orientations, the interpost intervals were divided into two categories depending on whether their orientation was more frontal or more radial. Radial distance was defined as being within 45° of the line of sight, and frontal distance was defined as being within 45° of the perpendicular, as measured from the observer’s position and the midpoint of the distance in the array. In the statistical analysis, only pairs for which one distance was radial and one was frontal were included. For instance, the pair comprising a frontal distance [1, 5] and a radial distance [1, 7] complied with this rule (see Fig. 2). Conversely, pairs comprising two radial or two frontal distances were excluded from further analysis. Of the 495 pairwise comparisons available, 260 satisfied the above criteria.

Fig. 2
figure 2

A sample pair of interobject distances that complied with the frontal–distal rule

Full size image

The data were fit with a logistic psychometric function with two parameters: threshold and slope. The threshold was determined as the ratio of the radial to the frontal distance required to achieve 50 % correct discriminations. For instance, the value 1.080 means that for a given frontal distance, a radial distance at least 1.08 times as large would be needed for the interval to be perceived as larger. This parameter corresponds to the systematic error. The slope negatively corresponds to consistency; that is, a steeper slope indicates better discrimination ability.

For the small-scale configuration, the threshold values for detecting radial distances as being larger than the frontal distances were 8.0 %, 9.8 %, and 10.6 % for the ordinal, ratio, and magnitude tasks, respectively. For the large-scale configuration, the thresholds for the same tasks were 20.4 %, 25.8 %, and 23.9 %, respectively. That is, although the precision of the observers’ relative distance judgments was generally higher for the ordinal task, considerable compression remained in the in-depth dimension, relative to the frontoparallel distance. This compression was similar to the distortion reported by Loomis et al. (2002) and, interestingly, was much lower than the distortions reported by Wagner (1985), Loomis et al. (1992), Norman et al. (1996), Loomis and Philbeck (1999), and Kudoh (2005). Such a difference, however, is not very surprising, given that both the in-depth and the frontal intervals encompassed a wide range of stimulus orientations. Additionally, the finding of greater compression for the large-scale stimulus configuration is unsurprising when one considers the retinal sizes of the intervals compared at the two scales (see the Discussion and Conclusions section). Our findings are consistent with those reported in previous studies (Baird & Biersdorf, 1967; Loomis et al., 1992; Loomis & Philbeck, 1999; Loomis et al., 2002; Šikl & Šimeček, 2011), which showed that the compression of the radial dimension grows as its distance from the observer increases. A two-way ANOVA performed on the threshold values for the psychometric functions confirmed that the relative distance judgments were not significantly different between measurement levels, F(2, 30) = 0.75, p = .48, η p 2 = .001. A Bonferroni post hoc test revealed that no pairwise difference was statistically significant. In contrast, the effect of scale was significant, F(1, 30) = 29.58, p < .001, η p 2 = .004, with this difference being apparent in all three tasks. No significant interaction effect was observed, F(2, 30) = 0.18, p = .84, η p 2 = .001.

The slope of the psychometric function (which reflects variability between observers) was steeper (i.e., judgments were less variable) for the ordinal estimations than for either the ratio or the absolute-magnitude estimations (see Table 2). A two-way ANOVA performed on the scale values for the fitted psychometric functions revealed a significant effect of measurement level, F(2, 30) = 8.07, p < .01, η p 2 = .037. Specifically, the pairwise comparisons were significantly different for the ordinal versus the absolute-magnitude (Bonferroni, p = .001) and ratio (Bonferroni, p = .03) estimations. The differences between the small- and large-scale data were also significant, F(1, 30) = 26.35, p < .001, η p 2 = .06, and were more pronounced for the ordinal task. Moreover, the ANOVA revealed no interaction between the measurement level and scale, F(2, 30) = 2.33, p = .12, η p 2 = .01.

Table 2 Threshold and slope of the psychometric functions of the ordinal, ratio, and magnitude responses
Full size table

Metric scale of measurement

It is not surprising that the data obtained in the ratio and absolute-magnitude distance judgment phases could be transformed to the ordinal level of measurement. However, the inverse transformation was also possible. Multidimensional scaling (MDS) enables the transformation of ordinal categorical data to the interval level of measurement (Young & Null, 1978). In principle, the same procedure was used in all three phases of the experiment: Using the raw data in the form of orders, ratios, and absolute magnitudes of the interpost distances, the perceived positions of the posts in each stimulus spatial configuration were calculated and compared with the actual layout within which the observers made their assessments.Footnote 3 That is, the nontransformed data were used in the analysis.

The data were analyzed as row-conditional, square-asymmetric matrices using the ALSCAL algorithm (Young & Harris, 1990). Procrustes analysis (including translation, rotation, and scaling) was then used to match the configurations obtained using MDS to a target configuration. The magnitude of visual space distortion relative to physical space in the individual tasks was measured using a parameter of MDS analysis, the sum of squared errors (SSE). The sum-of-squared-error measure was based on the sum of the squared deviations of the individual data points around the correct physical location. The units are given in meters. In addition, Kruskal’s stress formula I value was calculated as a measure of the goodness of fit between the perceived and actual locations of the stimulus points.

As can be seen in Fig. 3 and Table 3, the precision with which the perceived locations of the objects in the scene matched the true locations decreased as the measurement level increased. On average, for the small-scale configuration, the SSE values were 1.55, 2.53, and 3.28 for the ordinal, ratio, and magnitude tasks, respectively. For the large-scale configuration, the SSEs for the same tasks were 4.56, 8.83, and 11.86, respectively. These values correspond to mean absolute errors of approximately 4, 5, and 6 cm for the small-scale configuration, and approximately 19, 27, and 30 cm for the large-scale configuration. Comparison of these errors with the range of interpost distances presented in the experiment (0.5 to 3.0 m in the small-scale and 1.4 to 8.9 m in the large-scale configuration) indicated that the observers exhibited generally good precision for all types of judgments, particularly for the small-scale stimuli (cf. Levin & Haber, 1993; Toye, 1986). A two-way ANOVA performed on the SSEs yielded a significant effect for measurement level, F(2, 30) = 4.71, p = .02, η p 2 = .063. Specifically, the pairwise comparisons differed significantly between the ordinal and absolute-magnitude estimations (Bonferroni, p = .01). In contrast, the observers presented similar depth structures between the ordinal and ratio estimations and between the ratio and absolute-magnitude estimations. The difference between the small- and large-scale data was significant, F(1, 30) = 24.44, p < .001, η p 2 = .164. In contrast, the Level × Scale interaction proved nonsignificant, F(2, 30) = 1.80, p = .18, η p 2 = .02.

Fig. 3
figure 3

Multidimensional maps superimposed onto each stimulus configuration. Each post location is indicated by a cross, and each solid circle represents a particular response (i.e., a perceived location) to the corresponding post

Full size image
Table 3 Multidimensional-scaling stress (Kruskal I) and the root-mean squared error (RMSE)
Full size table

The same data pattern was also seen in the consistency of responses. On average, for the small-scale configuration, the Kruskal’s stress values were 0.01, 0.02, and 0.05 for the ordinal, ratio, and magnitude tasks, respectively. For the large-scale configuration, the values for the same tasks were 0.01, 0.02, and 0.06, respectively. A two-way ANOVA performed on the Kruskal’s stress values revealed a significant effect of measurement level, F(2, 30) = 29.08, p < .001, η p 2 = .243. Specifically, the pairwise comparisons significantly differed between the absolute-magnitude and ordinal estimations (Bonferroni, p < .001) and between the absolute-magnitude and ratio estimations (Bonferroni, p < .001), indicating less consistency in the observers’ judgments for the absolute-magnitude task. Even in this case, however, the values were less than 0.1, which is considered acceptable representation with little risk of misinterpreting the data. No significant main effect of scale emerged, F(1, 30) = 2.84, p = .10, η p 2 = .012, and there was no significant interaction effect, F(2, 30) = 0.62, p = .55, η p 2 = .005.

Discussion and conclusions

The aim of the present study was to investigate how levels of description requirements affect visual space perception. Three equivalent experimental tasks were conducted in which the observers estimated interobject distances in one of the following ways: While making ordinal distance judgments, they determined a distance ranking order; while making ratio distance judgments, they determined the ratio of test to reference length intervals; and while making absolute-magnitude distance judgments, they verbally estimated the lengths of all interpost intervals. In all three phases of the experiment, perceptual performance was first evaluated using an ordinal scale; subsequently, multidimensional scaling was used to determine the spatial configurations that were most consistent with the observers’ judgments. We found that regardless of the applied analysis, the precisions as well as consistencies of the observers’ interobject distance judgments were higher with lower levels of description requirements. Specifically, when an ordinal description of the layout was sufficient to determine the relative distance information, the observers produced errors less frequently, the discrimination thresholds were lower, the perceived positions of the posts better matched the actual positions, and the variability of the observers’ judgments was lower. Although the differences in results between the individual phases were not extreme (see the values for effect size estimates), the effect was statistically significant, with one exception.

On the basis of the literature, one might expect that different operationalizations of depth might yield different results (e.g., Da Silva, 1985; Rogers & Gogel, 1975; Nefs et al., 2013; Norman, Crabtree, Clayton, & Norman, 2005; Wagner, 1985). In psychophysical research, however, a wide variety of different methods and experimental procedures are used, and observers’ judgments are accepted at face value by investigators as valid estimates of a perceived spatial relationship. In the present study, we proposed three experimental procedures that had similar designs. However, this design similarity does not automatically mean that the observers used the same perceptual strategies in all of the tasks. We used the data collected during the inquiry to draw inferences about the computational requirements and developed hypotheses about the processes involved in making the three types of judgments required by the tasks.

Let us consider them now more in detail. In the ordinal distance task, the observers were asked to rank the posts in the stimulus array according to their distances from the reference standard. To make judgments while considering all ten length intervals simultaneously was clearly beyond the limits of the observers’ working memory capacity. Therefore, they first divided a group of intervals into smaller clusters that typically contained between two and four intervals that were phenomenologically different from the remaining intervals. Only after making this first, rough selection did they begin to perceptually distinguish between in-group distances and rank the posts. Typically, they hypothesized which of the posts was the closest (or the next in the list of posts) and tested this hypothesis by constructing imaginary circles or triangles between the reference and in-group posts. When all of the intervals from the first cluster were ordered, the observers divided the group of the remaining intervals to create a second cluster, continuing this procedure until the ranking was complete.

In the ratio distance task, the observers were asked to judge relative lengths on a ratio scale. As in the ordinal task, they first divided the group of length intervals into smaller clusters and, through hypothesis testing, selected the closest post—that is, the shortest length interval. This interval was treated as the unit length in the subsequent judgments and was used as a reference standard to which all ten remaining lengths were perceptually compared. The reference was mentally transposed and inserted into the given comparison interval, after which the ratio of the two lengths was estimated. The estimation process was repeated until a subjectively precise estimation was made (or, in other words, even more precise estimation would be performed without certainty). Notably, in the ratio task, unlike in the ordinal task, the observers, because of the fixed order of the trials, often had to process widely differing pairs of lengths in their subsequent judgments.

In the absolute-magnitude distance task, the observers were asked to judge the length of a single interval in centimeters. The procedure used to perform this task was straightforward. As expected, the observers mentally inserted the representation of 1 m (or any other unit) into the given comparison interval to determine the ratio between the physical and imaginary lengths. As in the ratio task, the estimations were refined iteratively, though not to the same extent, because the reference standard was subjective and the perceptual comparison might not therefore have been immediate. Taken together, when compared to the ordinal and ratio tasks, the absolute-magnitude task was likely less demanding on the observers’ working memory, because the computations needed to perform the perceptual task had the fewest number of stages. On the other hand, several sources of noise may have affected the observers’ responses in this task. For example, it required the observers to perform mental operations on lengths that were not physically present but only represented in their minds. This difficulty, together with the requirement to convert the perceived lengths into centimeters or ratios, would lead to lower certainty and add noise to the observers’ responses. To conclude, due to multiple factors, it would be difficult if not impossible to unambiguously determine whether the computational requirements of particular tasks were in accordance with the data obtained. However, this does generally seem to be the case.

Our subjects were asked to make a large number of judgments in the experiment, and their fatigue may have increased considerably during the sessions, particularly when making more cognitively demanding judgments in the ratio and absolute-magnitude distance tasks. This raises the question of whether fatigue may have led to poorer judgment precision—that is, whether the perceptual performance was affected by fatigue, boredom, and inattention rather than the depth description levels required by the experimental tasks. To evaluate the effect of fatigue on the observers’ judgments in each of the three phases, change of performance over time was measured. Importantly, higher or lower precision in any given part of the experiment does not directly correspond to a change in performance level, and consequently reveals litle about an observers’ fatique, given that the theoretical difficulty of the tasks—that is, the absolute and relative interpost distances that were perceptually compared—varied widely during the experiment. The data from the observers were split into two halves. The first half comprised judgments about Reference Posts 1–6 (270 responses), which were made earlier; the second half comprised judgments about Reference Posts 7–11 (225 responses). For each of the experimental tasks, the number of erroneous responses, which was treated as an ordinal variable, was then computed. If fatigue played a significant negative role in observers’ ratio and absolute-magnitude distance judgments, then the proportions of errors in the first and the second halves here would be different—that is, lower—than the error proportion found for the ordinal distance judgments. However, a chi-square test revealed that this difference, though detected, was not significant, χ 2(5) = 4.33, p = .5. In sum, possible fatigue of the observers does not account for the superiority of the ordinal method.

In the present study, we have questioned the validity of such judgments by comparing the precisions and consistencies with which observers can estimate spatial orders, ratios, and absolute magnitudes. In some sense, our study has some similarities to the studies by Todd and colleagues (Norman & Todd, 1998; Todd & Reichel, 1989), who compared observers’ abilities to discriminate ordinal and interval depth. On the basis of the data, they suggested that observers’ knowledge of smoothly curved surfaces can often involve a form of ordinal representation, in which neighboring surface regions are labeled in terms of which region is closer. The focus of these studies, though, was the description of visual form perception, and the authors examined the ability to judge much smaller depths in an indoor (laboratory) context.

Even more significant was the difference in perceptual performance between our small-scale and large-scale stimuli, the former resulting in better average performance (see also Baird & Biersdorf, 1967; Loomis et al., 1992; Loomis et al., 2002; Norman et al., 1996; Šikl & Šimeček, 2011, 2014). However, this finding is not surprising, considering the pairs of interobject distances in terms of their retinal sizes at either scale. For instance, for the pair comprising a radial distance [3, 7] and a frontal distance [3, 10], the ratio of the physical lengths was 1.39. The ratio of retinal sizes between the given distances was 0.6 in the small-scale configuration, but 0.27 in the large-scale configuration. That is, the extent of the image deformation and, consequently, the requirements for rescaling the image localizations were much higher at greater distances.

The tasks that required Euclidean knowledge of depth relationships were found to be more difficult for the observers than ordinal judgments, which is in line with previous studies (Norman & Todd, 1998; Todd & Reichel, 1989). In addition to these basic experimental data, we also observed that in responding to tasks that required higher orders of measurement, the observers exhibited increased response latencies; the observers also reported lower subjective confidence and were more tempted to apply cognitive corrective strategies. All of these findings raise questions about the ecological validity of many commonly used experimental tasks, which may be perceived by observers as unnatural or unnecessarily complicated. However, the metric properties of visual space (such as relative distance) can also be judged nonmetrically, which simplifies the process of judging perceptual depth relationships. Although the information extracted is of a less precise form, ordinal descriptions of depth have psychological relevance to human perception (Norman & Todd, 1992; Todd & Reichel, 1989), and ordinal-level information might suffice for many vision tasks (Gibson, 1950). Importantly, we do not assert that human observers represent physical space ordinally or that the units used to scale spatial layout are ordinal in nature. Our experiments were not designed to address this question. Neither do we assert that observers are able to recover ordinal depth with perfect accuracy (see, e.g., the perceptual anisotropy between frontal distances and distances in depth). The aim of the present article was to draw attention to the less-considered risks of using complex tasks that emphasize ratio or absolute levels of measurement in experiments on visual space perception. We attempted to show that these tasks are subjectively substantially more difficult for observers than everyday-life tasks. High demands put on observers due to task complexity may produce fatigue and lead to inattention. Observers are more prone to applying artifactual, cognitive-corrective strategies in an attempt to reduce the expected perceptual errors. Not surprisingly, then, the high demands of Euclidean tasks may lead to lower the consistency and precision with which perceptual judgments are made. Ignoring these methodological issues in most studies of visual space perception may have led to surprisingly poor results. In the present study, we designed and evaluated a novel distance judgment task that might, in principle, be slightly complicated for the experimenter to implement (e.g., more data have to be collected) and require less typical and less intuitive data analysis methods. From the observer’s perspective, however, this method of judgment is intuitive and provides higher levels of accuracy and reliability.