Abstract
In surveys concerning sensitive behavior or attitudes, respondents often do not answer truthfully, because of social desirability bias. To elicit more honest responding, the randomized-response (RR) technique aims at increasing perceived and actual anonymity by prompting respondents to answer with a randomly modified and thus uninformative response. In the crosswise model, as a particularly promising variant of the RR, this is achieved by adding a second, nonsensitive question and by prompting respondents to answer both questions jointly. Despite increased privacy protection and empirically higher prevalence estimates of socially undesirable behaviors, evidence also suggests that some respondents might still not adhere to the instructions, in turn leading to questionable results. Herein we propose an extension of the crosswise model (ECWM) that makes it possible to detect several types of response biases with adequate power in realistic sample sizes. Importantly, the ECWM allows for testing the validity of the model’s assumptions without any loss in statistical efficiency. Finally, we provide an empirical example supporting the usefulness of the ECWM.
Similar content being viewed by others
Researchers predominantly rely on direct self-reports to estimate the prevalence of attributes, attitudes, and behaviors. When the topic under investigation is sensitive, however, the validity of such estimates is threatened by social desirability bias (Paulhus, 1991) since participants tend to provide answers that are in line with social norms. Consequently, self-reports may result in an overestimation of socially desirable and an underestimation of socially undesirable attributes (Krumpal, 2013; Tourangeau & Yan, 2007).
The randomized-response (RR) technique offers a promising means to counteract social desirability bias by asking questions indirectly. In the original related-questions variant of the RR technique proposed by Warner (1965), participants are instructed to either respond to a sensitive question or its negation depending on the outcome of a randomization procedure. For example, in a survey on cocaine use, participants might be instructed to roll a die and respond to either the question “Have you ever used cocaine?” when the die showed one of the numbers 1 to 5 (p = 5/6), or the question “Have you never used cocaine?” when the die showed the number 6 (1 − p = 1/6). Importantly, the randomization outcome (i.e., the number rolled) remains unknown to the experimenter. Hence, individual responses are no longer directly linked to an individual’s true status on the surveyed attribute, because neither “yes” nor “no” responses provide any immediate diagnostic value about an individual respondent’s cocaine use. Yet, on sample level, an estimate of the prevalence of cocaine use can be obtained, provided that the probability of answering either of the questions is known. This estimate is expected to be more valid, because the randomization device grants confidentiality, thus enhancing participants’ motivation to respond truthfully. However, the RR technique also requires that respondents understand the procedure, be willing to answer correctly, and trust the implementation (Hoffmann, Waubert de Puiseau, Schmidt, & Musch, 2017; Landsheer, van der Heijden, & van Gils, 1999).
The results from a meta-analysis on comparative validation studies suggest that the RR technique can indeed lead to higher prevalence estimates of socially undesirable attributes than do direct self-reports (Lensvelt-Mulders, Hox, van der Heijden, & Maas, 2005). However, comparative validation studies provide only weak evidence, in the sense that they rely on an indirect comparison of two prevalence estimates without knowledge of the correct, external validation criterion. In contrast, strong validation studies compare RR estimates to the known prevalence of a sensitive attribute (Hoffmann, Diedenhofen, Verschuere, & Musch, 2015). Empirically, these studies have provided converging evidence by showing that RR estimates fell closer to the true value than did estimates from direct questions (e.g., Hoffmann et al., 2015; Moshagen, Hilbig, Erdfelder, & Moritz, 2014). Nevertheless, the true prevalence was still underestimated in these studies. Moreover, some strong validation studies have failed to demonstrate that the RR outperforms direct questioning (Höglinger & Jann, 2016; Wolter & Preisendörfer, 2013). This mixed empirical evidence indicates that a sizable proportion of respondents may still disobey, or simply not understand, the RR instructions, in turn leading to biased prevalence estimates (Lensvelt-Mulders et al., 2005). To address this issue, advanced RR models have been proposed that aim at either detecting or avoiding nonadherence to the instructions. Here we apply a broad definition of instruction nonadherence that refers to any type of response behavior leading to violations of the assumptions of the underlying questioning model. Nonadherence thus includes deliberate concealing of one’s true status (self-protective responding), as well as less systematic response patterns resulting from, for example, misunderstanding or careless responding.
Examples of approaches aiming to estimate or account for instruction nonadherence include the cheating detection model (CDM; Clark & Desharnais, 1998) and the stochastic lie detector (SLD; Moshagen, Musch, & Erdfelder, 2012; for other approaches, see, e.g., Böckenholt, Barlas, & van der Heijden, 2009; Chang, Wang, & Huang, 2004; Gupta, Gupta, & Singh, 2002; van den Hout, Böckenholt, & van der Heijden, 2010). The CDM is an extension of the forced-response RR model (Dawes & Moore, 1980) and attempts to classify respondents as honest carriers of the sensitive attribute (π), honest noncarriers (β), or cheaters (γ). Cheaters are expected to disregard instructions completely and to pursue a self-protecting response strategy instead. In several validation studies, CDM estimates for the proportion of honest carriers exceeded estimates obtained via direct self-reports, thus meeting the “more is better” assumption (e.g., Moshagen, Hilbig, & Musch, 2011; Moshagen, Musch, Ostapczuk, & Zhao, 2010; Ostapczuk, Musch, & Moshagen, 2011). Moreover, the CDM indicated substantial proportions of cheaters (\( \widehat{\gamma}>0 \)), showing that cheating increased with topic sensitivity (Moshagen & Musch, 2012) and with demographic characteristics of the sample (Ostapczuk, Musch, & Moshagen, 2009). These results emphasize the importance of a cheating detection mechanism even in indirect questioning formats. However, as no assumptions about cheaters’ status with respect to the sensitive attribute are made, only a lower bound (\( \widehat{\pi} \), assuming that no cheaters are carriers) and an upper bound (\( \widehat{\pi}+\widehat{\gamma} \), assuming that all cheaters are carriers) of the prevalence can be obtained.
In contrast, the SLD, as an extension of Mangat’s (1994) RR model, assumes that only carriers of the sensitive attribute try to cover up their true status by disregarding instructions. To account for such self-protective behavior, responses from carriers are subdivided into being truthful or untruthful, respectively. In two validation studies, SLD estimates were higher than estimates from direct self-reports (Moshagen et al., 2012) and closer to the known true value, respectively (Moshagen et al., 2014). Furthermore, a substantial proportion of carriers were estimated to provide untruthful responses (see also Hilbig, Moshagen, & Zettler, 2015). In a recent comparative validation, however, the SLD overestimated the known prevalence of a nonsensitive control attribute (Hoffmann & Musch, 2016) suggesting that the inherent model assumption of all noncarriers adhering to the instructions might have been violated. Finally, a drawback of both CDM and SLD is their comparably low statistical efficiency (on top of the statistical inefficiency of all RR variants due to adding random noise to conceal the respondents’ true status; Ulrich, Schröter, Striegel, & Simon, 2012), which results from the inclusion of the additional parameters that need to be estimated.
As an alternative to nonadherence detection, the crosswise model (CWM; Tian & Tang, 2014; Yu, Tian, & Tang, 2008) aims at reducing, or even avoiding, nonadherence by providing symmetrical response options and easy-to-understand instructions. In the CWM format, two questions are presented simultaneously: a sensitive question, for which the prevalence is unknown and has to be estimated (e.g., “Have you ever used cocaine?”), and a nonsensitive question with known prevalence p (e.g., “Is your birthday between May and July?”; p ≈ 3/12).Footnote 1 Clearly, investigators may not have access to any information about the nonsensitive question, so as to protect respondents’ anonymity (e.g., a questionnaire should not ask for the date of birth if the month of birth is used as a randomization device). Instead of responding to either of these questions directly, participants are prompted to indicate whether their answers to the two questions are identical (either both “yes” or both “no”), or their answers are different (one “yes,” the other one “no”).
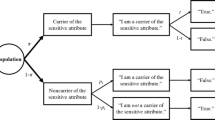
As is illustrated in Fig. 1, the probability λ of observing “Option A” (both “yes” or both “no”) responses is given by λ = πp + (1 − π)(1 − p). Despite the novel structure of the CWM in terms of survey design and psychological simplicity, it is mathematically equivalent to Warner’s original RR model outlined above. Hence, the ordinary least squares estimator of the prevalence of the sensitive question is given by
Tree diagram of the standard CWM (Yu et al., 2008). π denotes the unknown proportion of carriers of the sensitive attribute; p denotes the known prevalence of the insensitive question (i.e., the randomization probability)
with an estimated variance of
where \( \widehat{\lambda} \) is the observed proportion of Option A responses. If this estimate is in the interval between 0 and 1, it is identical to the maximum likelihood estimate. Otherwise, it has to be truncated to the boundaries 0 and 1.
Within the CWM, none of the response options allow for an individual respondent being identified as a carrier of the sensitive attribute, so that the answers to the sensitive question remain confidential. Importantly, and in contrast to other RR designs, participants are not given the opportunity to resort to a “safe” answering option that would allow them to explicitly deny carrying the sensitive attribute. Such symmetrical answering schemes are expected to prevent respondents from cheating on the instructions and have been used to improve the validity of prevalence estimates obtained via the CDM (Ostapczuk, Moshagen, Zhao, & Musch, 2009). Beyond the symmetrical structure, the simplified instructions of the CWM presumably facilitate respondents’ comprehension of how their privacy is protected and how to choose the appropriate response option. Given higher levels of understanding, the perceived privacy protection increases, which in turn is expected to result in a higher proportion of truthful responses (Landsheer et al., 1999). In line with this reasoning, the CWM has shown high levels of comprehensibility and subjectively perceived privacy protection in an experimental comparison of several indirect questioning techniques (Hoffmann et al., 2017). Moreover, the results from comparative validation studies (Hoffmann & Musch, 2016; Jann, Jerke, & Krumpal, 2012; Korndörfer, Krumpal, & Schmukle, 2014; Kundt, Misch, & Nerré, 2013; Nakhaee, Pakravan, & Nakhaee, 2013; Thielmann, Heck, & Hilbig, 2016; but see Höglinger, Jann, & Diekmann, 2016) and of one strong validation study with a known prevalence of the sensitive attribute (Hoffmann et al., 2015) suggest that the CWM outperforms competing approaches with respect to the control of social-desirability bias in sensitive surveys.
However, similar to any other RR variant, the validity of the CWM rests on the assumption that participants adhere to the instructions. Instruction nonadherence violates the inherent model assumptions, and might thus systematically bias the prevalence estimates (see Höglinger et al., 2016). For example, as explained in detail below, a tendency to overreport Option B responses (one “yes,” one “no”) will lead to an overestimation of π in case of p < .5, offering a potential alternative explanation for estimates meeting the “more is better” criterion. Unfortunately, the standard CWM does not provide a means to detect whether some of its assumptions are violated. As a remedy, borrowing ideas underlying the CDM and the SLD, we propose a straightforward two-group extension of the CWM that allows for detecting nonadherence to the instructions. Importantly, unlike the CDM or the SLD, this extended CWM (ECWM) is not associated with a loss in statistical efficiency as compared to the standard CWM.
The ECWM: An extension of the crosswise model
The core idea underlying the ECWM is to apply the CWM in an experimental setting that allows for obtaining a likelihood-ratio test with one degree of freedom. The outcome of this test can be used to judge whether nonadherence to the instructions has occurred, and thus whether the prevalence estimate can be considered trustworthy. To this end, the standard CWM is extended by randomly assigning participants to one of two (nonoverlapping) groups with group sizes n 1 and n 2 (n = n 1 + n 2), respectively. In both groups, respondents receive the same sensitive question, so that the prevalences of the sensitive attribute are expected to be identical across groups:
However, the two groups receive a different nonsensitive question in the CWM response format, which has a known prevalence of p in the first group (e.g., p ≈ 3/12 for the question “Is your mother’s birthday between May and July?”) and a complementary prevalence of 1 – p in the second group (e.g., 1 – p ≈ 9/12 for the question “Is your mother’s birthday between August and April?”). Correspondingly, two independent proportions of Option A responses, \( {\widehat{\uplambda}}_{A,1} \) and \( {\widehat{\uplambda}}_{A,2} \), are observed in Groups 1 and 2. Figure 2 illustrates the ECWM as a tree diagram, showing that the design essentially reverses responding between the groups.
Using the estimator for the standard CWM in Eq. 1, two independent prevalence estimates \( {\widehat{\pi}}_1 \) and \( {\widehat{\pi}}_2 \) are obtained by inserting the randomization probabilities p and 1 − p for Groups 1 and 2, respectively. Moreover, under the assumption that the prevalences are identical across groups, the ordinary least squares estimator \( \widehat{\pi} \) for the ECWM is given by inserting the pooled proportion
into the estimator for the standard one-group CWM in Eq. 1. Similarly, the estimated variance is given by inserting the pooled estimate \( \widehat{\lambda} \) in Eq. 2. If respondents fully understand and adhere to the CWM instructions (thus leading to π 1 = π 2), the group-specific prevalence estimates \( {\widehat{\pi}}_1 \) and \( {\widehat{\pi}}_2 \) will only differ by chance, which can be tested with an likelihood-ratio test with one degree of freedom (Read & Cressie, 1988). For this purpose, the binomial likelihood function for the randomization probabilities p 1 = p and p 2 = 1 − p and the data a i (the number of Option A responses in Group i) is used,
and evaluated twice: first for the saturated model using the two independent prevalence estimates \( {\widehat{\pi}}_1 \) and \( {\widehat{\pi}}_2 \), and second for the nested model using the pooled prevalence estimate \( \widehat{\pi} \) for both groups. The first model is saturated, because it has two free parameters to account for the two independent frequencies of choosing Option A in Groups 1 and 2, respectively, whereas the nested model, obtained as a special case by the equality constraint π 1 = π 2, has only one free parameter. If the assumptions of the (E)CWM hold, the separate estimates differ only by chance, and the likelihood-ratio test statistic
asymptotically follows a χ² distribution with one degree of freedom (i.e., the difference in the number of free parameters; Read & Cressie, 1988). In the supplementary materials (https://osf.io/mxjgf/), we provide R scripts for computing separate and pooled estimates for the ECWM as well as likelihood-ratio tests and also show how to obtain these estimates using the software RRreg (Heck & Moshagen, in press).
If the test turns out nonsignificant (and assuming that statistical power is sufficiently high; see below), the pooled estimate can be used with a standard error identical to that in the original CWM, thus resulting in the same statistical efficiency. In contrast, however, the validity of the CWM assumptions is questioned if differences in the irrelevant questions have actually affected the prevalence estimates across groups, as indicated by a significant likelihood-ratio test. In such a case, the prevalence estimates cannot be pooled and lack an unambiguous interpretation. Correspondingly, the ECWM provides a test of the assumptions underlying the (E)CWM and—when the test indicates that the assumptions were not violated—a pooled prevalence estimate without any loss of efficiency relative to the standard CWM. Essentially, this is achieved by using the reversed randomization probabilities p and 1 − p, which results in identical efficiencies of the estimators in both groups if n 1 = n 2 (since the standard error in Eq. 2 is symmetric for complementary randomization probabilities). Hence, even though the presentation format changes, the two groups of the ECWM are mathematically equivalent under full adherence to the instructions.
Detecting nonadherence in the ECWM
To investigate the sensitivity of the ECWM with respect to detecting instruction nonadherence (and thus, any potential violation of the model assumptions), we first introduce a conceptual framework of possible response biases in the CWM. Within this framework, we formalize different types of response biases and show which of these can be detected by the ECWM. Moreover, we determine the statistical power to detect violations of the ECWM assumptions in different scenarios.
A formal model of nonadherence
We define two conditional probabilities to operationalize instruction nonadherence. First, we assume that only some respondents will fully adhere to the CWM instructions. For this purpose, we define the probabilities c C and c N that carriers and noncarriers of the sensitive attribute (e.g., cocaine users and nonusers), respectively, will respond according to the CWM instructions. When both proportions c C and c N are equal to 1, all respondents adhere to the CWM instructions, thus resulting in a valid, unbiased prevalence estimate.
In contrast, when either of these proportions is smaller than 1, the assumptions of the (E)CWM are violated, and an alternative process determines the observed responses. To model this mechanism, which captures biases in favor of one of the response options (i.e., Option A or Option B), conditional on instruction nonadherence, we define the probabilities s C and s N that carriers and noncarriers would choose Option A, respectively. Figure 3 illustrates this hypothesized response process as a tree diagram of conditional probabilities. Psychologically, this model represents the assumption that participants might respond with Option A for different reasons—either Option A is the appropriate ECWM response, or it is merely selected as a result of instruction nonadherence (due to subjectively perceiving one of the options as being more safe, to misunderstanding, to careless responding, etc.). Note that the proposed model does not necessarily define nonadherence as strictly choosing the “wrong” option with respect to the RR instructions (e.g., always responding with Option B when the CWM instructions require responding with Option A, and vice versa). Instead, we adopt a broader definition according to which nonadherence can result in responses that match the CWM instructions by chance (e.g., an Option A response due to careless responding can still be “correct” according to the instructions). This allows for modeling psychologically different types of nonadherence, as we illustrate in the next section.
Tree diagram of the hypothesized response process within the ECWM. π denotes the unknown prevalence of carriers of the sensitive attribute; p i denotes the known randomization probabilities in Group i (p 1 = p, p 2 = 1 − p); c C and c N are the probabilities that the carriers and noncarriers in Group i will adhere to the instructions, respectively; and s C and s N are the corresponding probabilities to choose Option A, conditional on nonadherence
Biased prevalence estimates in the standard CWM
Before discussing the benefits of the ECWM, we use the response-bias framework to investigate how psychologically plausible response tendencies affect prevalence estimates in the standard CWM. Even though the CWM is a symmetric response format (i.e., both options can in principle indicate the sensitive attribute), one of the two options might be preferable subjectively. For instance, participants might show a general preference for Option B (one “yes” and one “no”) over Option A (both “yes” or both “no”), because the former might subjectively be perceived as a more typical “random pattern” according to the representativeness heuristic (Tversky & Kahneman, 1974). Given that randomness is conceptually related to anonymity, Option B might appear less incriminating and thus more attractive than Option A (as modeled by s C < .50, s N < .50).
To illustrate the effect of such a bias in favor of Option B (specifically, s C = s N = .10, representing a probability of 90% for both nonadherent carriers and nonadherent noncarriers to respond with Option B), Fig. 4A shows the estimator \( \widehat{\pi} \) as a function of the true prevalence π of a randomization probability of p = .25 and different adherence rates. If only half of all participants respond according to the instructions (c C = c N = .50), the true prevalence is overestimated substantially, especially when the true prevalence π is small. For example, a true prevalence of π = .10 is overestimated at \( \widehat{\pi} \) = .70 under these conditions. A similar effect is produced if only half of the noncarriers of the sensitive attribute do not adhere to the instructions, whereas carriers respond as instructed by the CWM (c C = 1.00, c N = .50). In contrast, the estimator shows little bias when all noncarriers of the sensitive attribute respond as instructed, whereas half of the carriers show nonadherence and prefer Option B (c C = .50, c N = 1.00).
Effects of two psychologically plausible response biases on prevalence estimates in the CWM with a known randomization probability p = .25. In panel A, a systematic preference for Option B is represented by s C = s N = .10, whereas in panel B, unsystematic responding is modeled by s C = s N = .50. Unbiased responding (i.e., full compliance, c C = c N = 1.00) is shown by the solid black lines in both panels
An alternative, psychologically plausible process for nonadherence is purely unsystematic random responding, which is modeled by s C = s N = .50 within the response-bias framework. As is illustrated in Fig. 4B, this response tendency results in a bias toward \( \widehat{\pi}=.50 \) for all true prevalences π if c C = c N. Likewise, the CWM results in a constant estimate \( \widehat{\uppi \uppi}=.50 \) irrespective of the true prevalence if all participants merely choose a response option randomly (in such an extreme case, the true prevalence π does not affect the observed responses anymore). This bias diminishes and finally disappears as the probability of adherence converges to c C = c N = 1. In contrast to this symmetric bias toward .50 given a single probability of nonadherence for all participants (c C = c N ), the true prevalences are generally underestimated if all noncarriers of the sensitive attribute adhere to the CWM instructions (c C = .50, c N = 1.00). Note that unsystematic responding will have similar effects in other response formats (including other RR formats and direct questioning) because it can be reframed as a shift of the true prevalence π toward .50.
Detectability of response biases in the ECWM
As we have derived above, the ECWM will result in identical prevalence estimates \( {\widehat{\pi}}_1 \) and \( {\widehat{\pi}}_2 \) per group if and only if \( {\widehat{\lambda}}_{A,1}=1-{\widehat{\lambda}}_{A,2} \). As a consequence, the method can only detect response biases that result in expected frequencies for which this equality does not hold. One such response bias is the general preference in favor of one of the two response options discussed in the previous section. For example, as is shown in Fig. 5A, the difference in prevalence estimates \( {\widehat{\pi}}_1-{\widehat{\pi}}_2 \) exceeds zero if 50% of the participants do not adhere to the ECWM instructions and instead prefer Option B (i.e., choose Option A with probability s C = s N = .10). Importantly, this response tendency can also be detected if either only carriers or only noncarriers of the sensitive attribute do not adhere to the instructions (with the exception of extreme prevalences of π = 0 and π = 1, for which the CWM is not biased, as is shown in Fig. 4A).
Differences in prevalence estimates of both ECWM groups for two psychologically plausible response biases, given a known randomization probability of p = .25. In panel A, the preference for Option B is represented by s C = s N = .10, whereas in panel B, unsystematic responding is modeled by s C = s N = .50. All lines in panel B overlap at zero, implying that the ECWM cannot detect unsystematic responding
In contrast to a systematic preference for one response option, purely random responding (s C = s N = .50) is not detectable within the ECWM. Figure 5B shows that the prevalence estimates in both groups are identical—irrespective of the true prevalence and of whether 50% of all participants, only 50% of the carriers, or only 50% of the noncarriers resort to unsystematic responding.
In conclusion, the ECWM allows for detecting a specific, psychologically plausible type of nonadherence—that is, a systematic preference for one of the two response options. However, due to its symmetric structure, the ECWM cannot detect purely unsystematic responding.
Statistical power of the ECWM
As we elaborated above, the critical test concerns the null hypothesis that the observed relative frequencies of Option A responses are equal in both groups: λ A , 1 = 1 − λ A , 2. To assess the power of this test for differences between two independent binomial proportions, we used the normal approximation for relative frequencies also used by Ulrich et al. (2012). These results closely matched the results from simulations using the exact likelihood-ratio test discussed above. The following plots are based on a significance level of α = . 05.
Figure 6A shows the statistical power of the ECWM to detect a systematic preference for Option B (s C = s N = .10) for a sample size of n 1 = n 2 = 100 as a function of the true prevalence of the sensitive attribute (similar as in Fig. 5A). Even though this sample size is rather small relative to the samples typically recruited in RR studies (e.g., Hoffmann & Musch, 2016; Moshagen & Musch, 2012; Schröter et al., 2016; Thielmann et al., 2016), the ECWM has a high power to detect 50% nonadherence of all participants, irrespective of the true prevalence. In contrast, the power depends on the true prevalence if only carriers or only noncarriers show nonadherence. In line with Fig. 5A, the test is less likely to detect small differences between the two group-specific prevalence estimates (e.g., small prevalences of π < . 40 when only 50% of the carriers do not adhere to the instructions). As compared to these high rates of 50% nonadherence, Fig. 6B shows that the statistical power decreases if only 25% of either all participants, only carriers, or only noncarriers show nonadherence.
Statistical power to detect a systematic preference for Option B (probability of s C = s N = .10 to choose Option A) with n 1 = n 2 = 100 and (A) low and (B) high adherence rates (i.e., c = 50% vs. 75%, respectively), for all participants, carriers, or noncarriers. The solid black lines reflect the significance level of α = 5%, defined as the probability of falsely rejecting the null hypothesis given that all participants actually adhered to the instructions
For practical applications, it is of most interest to compute the minimum required sample size to detect a specific level of instructions nonadherence. On the basis of a systematic preference in favor of Option B (s = .10), Fig. 7 shows the statistical power as a function of sample size for varying prevalence and adherence rates across row and column panels, respectively. If nonadherence is substantial (c = .40 or .60), sample sizes below n = 200 suffice to detect instruction nonadherence of all participants or of only noncarriers with a power of 80%, whereas n = 600 is required if most respondents follow the instructions (c = .80). In contrast, the power is generally low if only carriers show a preference for Option B. This is due to the small prevalence rates, because only a small proportion of all participants will violate the assumptions [i.e., π · (1 − c)]. Obviously, detecting whether this proportion is larger than zero requires large samples sizes, as is shown in Fig. 7. However, in such cases the prevalence estimates will be biased to only a small degree.
Empirical example
As an empirical example, we illustrate the application of the ECWM using two sensitive questions concerning performance-enhancing substances and sexually transmitted diseases. For the second of the sensitive questions, we deliberately used conditions that make instruction nonadherence likely to occur. Data and scripts for analysis are available in the supplementary material.
Method
We recruited 322 students of a medium-sized German university (173 male, 149 female; mean age = 22.4 years) to answer a questionnaire testing a novel survey procedure. All instructions and questions fitted on a single page to ensure short completion times. This also had the effect that almost all questionnaires returned were filled out completely (six respondents did not report their age, and one did not report age and sex; there were no missing responses on either sensitive question; the analysis lead to identical conclusions when excluding these seven participants). Participants were instructed that the procedure fully protects their anonymity by requiring only a single response to two questions:
-
A.
their answers to the two questions are identical (either both “yes” or both “no”), or
-
B.
their answers are different (one “yes,” the other “no”).
To increase understanding of the instructions, a written-out example showed how to choose the appropriate response option, case by case. For the first sensitive question, we used the same irrelevant question as in the preceding examples:
-
i.
“Is your mother’s birthday between May and July?”
-
ii.
“Did you ever consume a performance-enhancing substance (e.g., Ritalin)?”
For the second sensitive question, we attempted to create conditions that would increase the likelihood of instruction nonadherence. In particular, we used a less optimal randomization scheme by asking for the father’s birthday (not all people know their father) and switching the months in the irrelevant question as compared to the written-out example and the first question (thereby increasing the likelihood of errors due to skimming):
-
i.
“Is your father’s birthday between August and April?”
-
ii.
“Did you ever have a sexually transmitted disease?”
Changing such minor details of the irrelevant question in the sequential application of the (E)CWM is not advisable in practice, because these changes are likely to be overlooked. Hence, the nonoptimal randomization scheme for the second question is more likely to result in erroneous responses. If this prediction holds, the ECWM should exhibit a poor fit for the second question, thereby indicating that the obtained prevalence estimates are not trustworthy.
The questionnaire for the second group differed only regarding the months mentioned in the irrelevant question (i.e., “between August and April” and “between May and July” for the first and second sensitive questions, respectively). Note that the months used in the written-out example always matched those used for the first sensitive question, but they were different from those used for the second sensitive question. Participants were assigned to one of the groups by distributing the two versions of the questionnaire randomly.
Results
The two ECWM groups were nearly equally sized (n 1 = 159, n 2 = 163). For the first question, concerning performance-enhancing substances, 66 and 102 participants selected Option A in Groups 1 and 2, respectively. The ECWM fitted the data well, as indicated by a nonsignificant likelihood-ratio test, G²(1) = 0.56, p = .453. This is in line with our expectation that using exactly the same irrelevant question as in the example would enhance understanding of the CWM instructions. The prevalence estimate was \( \widehat{\pi} \) = .289 (SE = .055). Note that this rather high estimate might be due to the formulation of the question, which did not explicitly ask for illegal performance-enhancing substances. Hence, despite the reference to Ritalin, some participants might have considered legal drugs such as coffee or energy drinks, as well. Moreover, it is possible that some respondents reported having used Ritalin as a medication for ADHD, rather than as a performance-enhancing drug. However, because we expected the frequency of such responses to be very small in the present sample, the effects on the estimates obtained would be negligible. Importantly, the nonsignificant likelihood-ratio test indicated that the assumptions of the ECWM were not violated.
For the second question, concerning sexually transmitted diseases, 109 and 71 participants chose Option A in Groups 1 and 2, respectively. This resulted in a significant likelihood-ratio test, G²(1) = 5.05, p = .025. As we expected, the changes in the sequential application of the ECWM (i.e., switching from mother to father and changing the months in the irrelevant question without highlighting these changes) resulted in a response pattern inconsistent with the assumptions of the CWM, which, in turn, could be detected by the ECWM. Given that the model did not fit the data, the high prevalence estimate of \( \widehat{\pi} \) = .252 (SE = .054) of respondents with sexually transmitted diseases is not trustworthy and should not be interpreted.
Discussion
The CWM (Yu et al., 2008) offers a promising means to address socially desirable responding in surveys on sensitive personal attributes. The validity of prevalence estimates obtained via CWM questions, however, depends on the assumption that all participants adhere to the instructions. This assumption cannot be tested within the standard CWM. To address this issue, we proposed an extended CWM, the ECWM, in which the randomization probability is experimentally manipulated across two randomly assigned groups. This extension allows for testing the fit of the model by assessing differences in prevalence estimates across groups via an likelihood-ratio test with one degree of freedom. Within a novel conceptual framework for response biases in the CWM, we showed that specific types of nonadherence—that is, a general preference for one of the two answer options—threaten the validity of the prevalence estimates obtained and that the ECWM is capable of detecting such biases with sufficient power (under typical conditions). We further illustrated the utility of the ECWM in an empirical application to two questions with optimal versus nonoptimal randomization schemes. As expected, this manipulation resulted in good versus poor fit of the ECWM, respectively. Hence, the ECWM is expected to improve on the original CWM by offering a means to detect specific types of instruction nonadherence without loss in statistical efficiency. Moreover, due to its similarity to the original CWM and the Warner model, the ECWM can directly be analyzed with software for the multivariate analysis of RR data such as the R package RRreg (Heck & Moshagen, in press), for example, to predict sensitive behavior using a logistic regression.
Despite the utility of the ECWM, certain limitations of the model should also be considered. Whereas the ECWM can indicate whether the estimates are trustworthy, it cannot reveal any information about possible sources of misfit (i.e., particular reasons for instruction nonadherence). Moreover, the ECWM neither offers a means of estimating the extent to which instruction nonadherence occurred nor provides a prevalence estimate that corrects for instruction nonadherence. Nevertheless, the ECWM does allow for generally evaluating whether prevalence estimates can be trusted or not. In practical applications of indirect questioning techniques, this extension clearly offers useful additional information, and—again, in contrast to competing approaches such as the CDM or the SLD, respectively—is not connected to any additional costs with respect to efficiency, as no additional parameters have to be estimated.
It should also be noted that a nonsignificant likelihood-ratio test does not necessarily imply the absence of nonadherence. A low extent of nonadherence or a small sample size are associated with low statistical power to detect possible violations of the model assumptions. Furthermore, the ECWM is incapable of detecting instruction nonadherence that is due to pure random guessing between the two response options. This model property might be problematic in cases in which random guessing is likely to occur, for example, if respondents possess limited cognitive abilities or simply do not pay attention to the instructions. However, random guessing impedes on the validity not only of prevalence estimates obtained via the ECWM, but also of estimates based on direct questions and most other RR designs. Furthermore, within indirect questioning techniques, the CWM has been shown to be among the most comprehensible formats (Hoffmann et al., 2017). Easily understandable instructions, possibly combined with preliminary questions that assess instruction comprehension, might thus maximize participants’ motivation to engage in the procedure and to refrain from responding randomly (Hoffmann et al., 2015). Moreover, the response-bias framework proposed in the present work might facilitate the development of refined models that are more sensitive to various types of instruction nonadherence.
Overall, the ECWM offers many benefits. For respondents, the instructions are as easy to understand as those in the standard CWM and can thus be expected to elicit more honest responding. For researchers, the method provides a crucial test for instruction nonadherence while being as efficient as the original model version. In the present application, we showed that the ECWM was able to detect instruction nonadherence due to suboptimal questionnaire design. In future studies, the ECWM could be used to test more substantive research questions, for instance, whether instruction nonadherence is more likely when the sensitivity of the question increases despite the privacy protection provided by the CWM. Taken together, the ECWM offers additional value without additional costs and thus represents a useful method for investigating sensitive attitudes and behavior.
Author note
D.W.H. was supported by the University of Mannheim’s Graduate School of Economic and Social Sciences funded by the German Research Foundation. We thank Andreas Decker for data collection. Data and R scripts are available at the Open Science Framework, https://osf.io/mxjgf/.
Notes
According to official birth statistics, the prevalence values for children born between May and July in Germany were 25.5% and 25.6% in the years 1990 and 2000, respectively (Statistisches Bundesamt, 2012). Note that sampling variation of the relative frequency of corresponding birthdays (e.g., if only 270 out of 1,200 respondents are born between May and July) is taken into account by the statistical model and by the corresponding standard error of the prevalence estimate.
References
Böckenholt, U., Barlas, S., & van der Heijden, P. G. M. (2009). Do randomized-response designs eliminate response biases? An empirical study of non-compliance behavior. Journal of Applied Econometrics, 24, 377–392. doi:https://doi.org/10.1002/Jae.1052
Statistisches Bundesamt. (2012). Geburten in Deutschland. Retrieved from https://www.destatis.de/DE/Publikationen/Thematisch/Bevoelkerung/Bevoelkerungsbewegung/BroschuereGeburtenDeutschland0120007129004.pdf?__blob=publicationFile
Chang, H.-J., Wang, C.-L., & Huang, K.-C. (2004). Using randomized response to estimate the proportion and truthful reporting probability in a dichotomous finite population. Journal of Applied Statistics, 31, 565–573. doi:https://doi.org/10.1080/02664760410001681819
Clark, S. J., & Desharnais, R. A. (1998). Honest answers to embarrassing questions: Detecting cheating in the randomized response model. Psychological Methods, 3, 160–168. doi:https://doi.org/10.1037/1082-989X.3.2.160
Dawes, R. M., & Moore, M. (1980). Die Guttman-Skalierung orthodoxer und randomisierter Reaktionen [Guttman scaling of orthodox and randomized reactions]. In F. Petermann (Ed.), Einstellungsmessung, Einstellungsforschung [Attitude measurement, attitude research] (pp. 117–133). Göttingen: Hogrefe.
Gupta, S., Gupta, B., & Singh, S. (2002). Estimation of sensitivity level of personal interview survey questions. Journal of Statistical Planning and Inference, 100, 239–247. doi:https://doi.org/10.1016/S0378-3758(01)00137-9
Heck, D. W., & Moshagen, M. (in press). RRreg: An R package for correlation and regression analyses of randomized response data. Journal of Statistical Software.
Hilbig, B. E., Moshagen, M., & Zettler, I. (2015). Truth will out: Linking personality, morality, and honesty through indirect questioning. Social Psychological and Personality Science, 6, 140–147. doi:https://doi.org/10.1177/1948550614553640
Hoffmann, A., Diedenhofen, B., Verschuere, B. J., & Musch, J. (2015). A strong validation of the crosswise model using experimentally induced cheating behavior. Experimental Psychology, 62, 403–414. doi:https://doi.org/10.1027/1618-3169/a000304
Hoffmann, A., & Musch, J. (2016). Assessing the validity of two indirect questioning techniques: A stochastic lie detector versus the crosswise model. Behavior Research Methods, 48, 1032–1046. doi:https://doi.org/10.3758/s13428-015-0628-6
Hoffmann, A., Waubert de Puiseau, B., Schmidt, A. F., & Musch, J. (2017). On the comprehensibility and perceived privacy protection of indirect questioning techniques. Behavior Research Methods, 49, 1470–1483. doi:https://doi.org/10.3758/s13428-016-0804-3
Höglinger, M., & Jann, B. (2016). More is not always better: An experimental individual-level validation of the randomized response technique and the crosswise model (University of Bern Social Sciences Working Paper 18). Retrieved from http://econpapers.repec.org/paper/bsswpaper/18.htm
Höglinger, M., Jann, B., & Diekmann, A. (2016). Sensitive questions in online surveys: An experimental evaluation of different implementations of the randomized response technique and the crosswise model. Survey Research Methods, 10, 171–187.
Jann, B., Jerke, J., & Krumpal, I. (2012). Asking sensitive questions using the crosswise model. Public Opinion Quarterly, 76, 32–49. doi:https://doi.org/10.1093/Poq/Nfr036
Korndörfer, M., Krumpal, I., & Schmukle, S. C. (2014). Measuring and explaining tax evasion: Improving self-reports using the crosswise model. Journal of Economic Psychology, 45, 18–32. doi:https://doi.org/10.1016/j.joep.2014.08.001
Krumpal, I. (2013). Determinants of social desirability bias in sensitive surveys: A literature review. Quality and Quantity, 47, 2025–2047. doi:https://doi.org/10.1007/s11135-011-9640-9
Kundt, T. C., Misch, F., & Nerré, B. (2013). Re-assessing the merits of measuring tax evasions through surveys: Evidence from Serbian firms (ZEW Discussion Papers, No. 13-047). Retrieved Dec 12th, 2013, from http://hdl.handle.net/10419/78625
Landsheer, J. A., van der Heijden, P. G. M., & van Gils, G. (1999). Trust and understanding, two psychological aspects of randomized response—A study of a method for improving the estimate of social security fraud. Quality and Quantity, 33, 1–12. doi:https://doi.org/10.1023/A:1004361819974
Lensvelt-Mulders, G. J. L. M., Hox, J. J., van der Heijden, P. G. M., & Maas, C. J. M. (2005). Meta-analysis of randomized response research: Thirty-five years of validation. Sociological Methods and Research, 33, 319–348. doi:https://doi.org/10.1177/0049124104268664
Mangat, N. S. (1994). An improved randomized-response strategy. Journal of the Royal Statistical Society, Series B: Statistical Methodology, 56, 93–95.
Moshagen, M., Hilbig, B. E., Erdfelder, E., & Moritz, A. (2014). An experimental validation method for questioning techniques that assess sensitive issues. Experimental Psychology, 61, 48–54. doi:https://doi.org/10.1027/1618-3169/a000226
Moshagen, M., Hilbig, B. E., & Musch, J. (2011). Defection in the dark? A randomized-response investigation of cooperativeness in social dilemma games. European Journal of Social Psychology, 41, 638–644. doi:https://doi.org/10.1002/ejsp.793
Moshagen, M., & Musch, J. (2012). Surveying multiple sensitive attributes using an extension of the randomized-response technique. International Journal of Public Opinion Research, 24, 508–523.
Moshagen, M., Musch, J., & Erdfelder, E. (2012). A stochastic lie detector. Behavior Research Methods, 44, 222–231. doi:https://doi.org/10.3758/s13428-011-0144-2 21858604
Moshagen, M., Musch, J., Ostapczuk, M., & Zhao, Z. (2010). Reducing socially desirable responses in epidemiologic surveys: An extension of the randomized-response technique. Epidemiology, 21, 379–382. doi:https://doi.org/10.1097/Ede.0b013e3181d61dbc
Nakhaee, M. R., Pakravan, F., & Nakhaee, N. (2013). Prevalence of use of anabolic steroids by bodybuilders using three methods in a city of Iran. Addict Health, 5, 77–82.
Ostapczuk, M., Moshagen, M., Zhao, Z., & Musch, J. (2009). Assessing sensitive attributes using the randomized response technique: Evidence for the importance of response symmetry. Journal of Educational and Behavioral Statistics, 34, 267–287. doi:https://doi.org/10.3102/1076998609332747
Ostapczuk, M., Musch, J., & Moshagen, M. (2009). A randomized-response investigation of the education effect in attitudes towards foreigners. European Journal of Social Psychology, 39, 920–931. doi:https://doi.org/10.1002/ejsp.588
Ostapczuk, M., Musch, J., & Moshagen, M. (2011). Improving self-report measures of medication non-adherence using a cheating detection extension of the randomised-response-technique. Statistical Methods in Medical Research, 20, 489–503. doi:https://doi.org/10.1177/0962280210372843
Paulhus, D. L. (1991). Measurement and control of response bias. In J. P. Robinson, P. R. Shaver, & L. S. Wrightsman (Eds.), Measures of personality and social psychological attitudes (Vol. 1, pp. 17–59). San Diego: Academic Press.
Read, T. R., & Cressie, N. A. (1988). Goodness-of-fit statistics for discrete multivariate data. New York: Springer.
Schröter, H., Studzinski, B., Dietz, P., Ulrich, R., Striegel, H., & Simon, P. (2016). A comparison of the cheater detection and the unrelated question models: A randomized response survey on physical and cognitive doping in recreational triathletes. PLoS ONE, 11, e155765:1–11. doi:https://doi.org/10.1371/journal.pone.0155765
Thielmann, I., Heck, D. W., & Hilbig, B. E. (2016). Anonymity and incentives: An investigation of techniques to reduce socially desirable responding in the Trust Game. Judgment and Decision Making, 11, 527–536.
Tian, G.-L., & Tang, M.-L. (2014). Incomplete categorical data design: Non-randomized response techniques for sensitive questions in surveys. Boca Raton: CRC Press, Taylor & Francis Group.
Tourangeau, R., & Yan, T. (2007). Sensitive questions in surveys. Psychological Bulletin, 133, 859–883. doi:https://doi.org/10.1037/0033-2909.133.5.859 17723033
Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases. Science, 185, 1124–1131. doi:https://doi.org/10.1126/science.185.4157.1124
Ulrich, R., Schröter, H., Striegel, H., & Simon, P. (2012). Asking sensitive questions: A statistical power analysis of randomized response models. Psychological Methods, 17, 623–641. doi:https://doi.org/10.1037/A0029314
van den Hout, A., Böckenholt, U., & van der Heijden, P. (2010). Estimating the prevalence of sensitive behaviour and cheating with a dual design for direct questioning and randomized response. Journal of the Royal Statistical Society, Series C: Applied Statistics, 59, 723–736. doi:https://doi.org/10.1111/j.1467-9876.2010.00720.x
Warner, S. L. (1965). Randomized response: A survey technique for eliminating evasive answer bias. Journal of the American Statistical Association, 60, 63–69.
Wolter, F., & Preisendörfer, P. (2013). Asking sensitive questions: An evaluation of the randomized response technique versus direct questioning using individual validation data. Sociological Methods & Research, 42, 321–353. doi:https://doi.org/10.1177/0049124113500474
Yu, J.-W., Tian, G.-L., & Tang, M.-L. (2008). Two new models for survey sampling with sensitive characteristic: design and analysis. Metrika, 67, 251–263. doi:https://doi.org/10.1007/s00184-007-0131-x
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Heck, D.W., Hoffmann, A. & Moshagen, M. Detecting nonadherence without loss in efficiency: A simple extension of the crosswise model. Behav Res 50, 1895–1905 (2018). https://doi.org/10.3758/s13428-017-0957-8
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13428-017-0957-8