Abstract
This article introduces a new computational model for the complex-span task, the most popular task for studying working memory. SOB-CS is a two-layer neural network that associates distributed item representations with distributed, overlapping position markers. Memory capacity limits are explained by interference from a superposition of associations. Concurrent processing interferes with memory through involuntary encoding of distractors. Free time in-between distractors is used to remove irrelevant representations, thereby reducing interference. The model accounts for benchmark findings in four areas: (1) effects of processing pace, processing difficulty, and number of processing steps; (2) effects of serial position and error patterns; (3) effects of different kinds of item–distractor similarity; and (4) correlations between span tasks. The model makes several new predictions in these areas, which were confirmed experimentally.
Similar content being viewed by others
Working memory can be characterized as a system for holding a limited amount of information available for processing. Its limited capacity has been shown to have considerable generality across various contents and methods of measurement (Kane et al., 2004; Oberauer, Süß, Schulze, Wilhelm, & Wittmann, 2000). Variations in working memory between groups and between individuals have been shown to correlate with performance in a broad range of complex cognitive activities (for a review, see Conway, Jarrold, Kane, Miyake, & Towse, 2007).
The most commonly used paradigm for measuring working memory capacity is the complex-span paradigm. There are several variants of complex span, the earliest being the reading span (Daneman & Carpenter, 1980) and counting span (Case, Kurland, & Goldberg, 1982) tasks, later followed by operation span (Turner & Engle, 1989) and spatial variants of the paradigm (Shah & Miyake, 1996). The general schema of all complex-span tasks is that encoding of a list of memoranda (e.g., words, letters) for serial recall is interleaved with a distracting processing task (e.g., reading a sentence or verifying an equation). The term complex span has been coined in contrast to simple span, which refers to immediate serial recall without a parallel distractor task.
Multiple variants of complex span have been validated as measures of working memory capacity by the findings that they correlate well with each other and with other indicators of working memory capacity (Oberauer et al., 2000; Schmiedek, Hildebrandt, Lövdén, Wilhelm, & Lindenberger, 2009) and that they are good predictors of a range of performance indicators in tasks that are theoretically assumed to require working memory, such as tests of reasoning and fluid intelligence (Conway, Kane, & Engle, 2003), text comprehension (Daneman & Merikle, 1996), and explicit learning of a rule (Unsworth & Engle, 2005), as well as a number of experimental tasks requiring cognitive control, such as the Stroop task (Kane & Engle, 2003) and the antisaccade task (Unsworth, Schrock, & Engle, 2004). Therefore, understanding the cognitive processes in the complex-span paradigm would be a fundamental step toward understanding the capacity limits of cognition. The success of complex span as a measure of working memory capacity has inspired much experimental work and various theoretical efforts directed at analyzing the underlying processes (e.g., Barrouillet, Bernardin, & Camos, 2004; Bayliss, Jarrold, Gunn, & Baddeley, 2003; Engle, Cantor, & Carullo, 1992; Oberauer & Lewandowsky, 2011; Towse, Hitch, & Hutton, 2000; Unsworth & Engle, 2007).
With few exceptions, theories of the processes involved in complex span, like theories of working memory in general, have so far remained verbal descriptions of mechanisms. This is problematic because it is generally acknowledged that working memory is a complex system, and comprehensive theories of working memory typically assume numerous mechanisms and processes that operate together (Baddeley, 1986; Cowan, 1995). With theories of such complexity, unambiguously determining predictions for a specific set of circumstances easily surpasses our human reasoning abilities (Farrell & Lewandowsky, 2010). The problem is often compounded by the vagueness of verbal theories, which leave many critical details unspecified (for an example, see Lewandowsky & Farrell, 2011). These problems can be addressed using computational modeling. Writing a theory as a computer program forces the theorist to specify the model in sufficient detail for the program to run. Moreover, running the program provides a means to derive precise and unambiguous predictions from the model. Every single decision on the way from the general principles of a theory to its detailed implementation, and every step on the way to its predictions for a specific experiment, is fully transparent in the programming code.
Computational modeling has been applied fruitfully to one experimental paradigm of working memory research, the serial-recall task (Burgess & Hitch, 1999; Farrell & Lewandowsky, 2002; Henson, 1998b; Page & Norris, 1998). The goal of the present work is to apply what we have learned from modeling of serial recall to developing a computational model of behavior in the complex-span paradigm. This is no trivial step, because complex span appears to rely on core cognitive abilities to a far greater extent than does simple span. For example, even though the surface similarity between different complex-span tasks (e.g., operation span vs. sentence span) is far less than the surface similarity between simple-span tasks from different domains, performance correlates more highly across domains for the complex-span than for the simple-span task (Kane et al., 2004). Moreover, because the complex-span task shares many features with other paradigms of working memory research—short-term retention of information, a requirement to retain serial order, distraction by a concurrent task, and coordination of multiple competing processes—a computational model of complex span will serve as a springboard for more precise theorizing in the field as a whole.
One central theoretical question about working memory is why it has limited capacity. Many theories explain the capacity limit by assuming that representations in working memory quickly decay over time unless they are actively maintained by rehearsal or refreshing (Baddeley, 1986; Barrouillet et al., 2004). This assumption has been incorporated into the only two computational models of complex span proposed so far (Daily, Lovett, & Reder, 2001; Oberauer & Lewandowsky, 2011). The assumption of rapid time-based decay, however, has been repeatedly questioned by empirical observations (for a review, see Lewandowsky, Oberauer, & Brown, 2009). One common alternative to decay is that working memory capacity is limited by interference between representations (Jonides et al., 2008; Nairne, 2002; Saito & Miyake, 2004). To date, however, the concept of interference has remained underspecified, thus limiting its theoretical utility (Jonides et al., 2008). We overcome this limitation here by instantiating the interference notion in a detailed computational model of complex span.
Our model attributes the capacity limit of working memory entirely to interference. The model accounts for all of the findings that provided the initial empirical support for a decay-based theory of complex span, the time-based resource-sharing (TBRS) theory of Barrouillet, Camos, and colleagues (Barrouillet et al., 2004; Barrouillet, Bernardin, Portrat, Vergauwe, & Camos, 2007). The TBRS theory has, arguably, been the strongest contender for explaining complex-span performance to date, and therefore we will compare our new model to a computational implementation of the TBRS theory (Oberauer & Lewandowsky, 2011).
This article proceeds as follows: We start by presenting our model—first informally as a set of theoretical assumptions, and then formally as a computational instantiation. We then apply the model to four sets of empirical findings. These represent benchmark findings from the complex-span paradigm that should serve as priority targets for modeling. The first is a set of findings concerning the relation between short-term retention and the temporal parameters of concurrent processing. These findings provided the empirical basis for the TBRS theory (Barrouillet et al., 2007; Barrouillet, Portrat, & Camos, 2011). The second set of findings represents a detailed analysis of recall errors in complex span, which has proved highly informative for models of simple span. The third set of findings concerns the effects of different kinds of similarity between memory items and distractors. The fourth set pertains to the pattern of correlations between span tasks across different domains that arises from the study of individual differences. The model is shown to handle all four sets of findings.
A distributed neural-network model for complex span
Our model is an extension of the SOB (“serial-order-in-a-box”) model, a distributed neural-network model of serial recall (Farrell & Lewandowsky, 2002). The initial SOB was an auto-associator in the tradition of the brain-state-in-a-box (BSB) architecture (Anderson, Silverstein, Ritz, & Jones, 1977), from which the model derived its name. The second version, called C-SOB (Farrell, 2006; Lewandowsky & Farrell, 2008b), has a two-layer structure, with one layer representing serial positions and the other representing items (the prefix “C” stands for “context,” because the position representations are a form of context). Both item and position representations are distributed—that is, they consist of patterns of activation across a large number of processing units in the network. Different items are represented by different patterns across the same set of units. Thus, item representations have well-defined similarity relations to each other, reflected in the similarity of the patterns representing them; the same holds for positions. Items are encoded in C-SOB through Hebbian associations between item and position representations: The first list item is associated with the first position representation (a.k.a. a position marker), the second item is associated with the second position marker, and so on. Memory for order is maintained by the patterns of association in the weight matrix that connects position markers to item representations. The use of context markers to represent order is a standard tool among memory theorists and has gained substantial empirical support (Lewandowsky & Farrell, 2008b).
Memory performance is limited because all item-to-position associations are superimposed in the same weight matrix, so that at the point of recall the matrix represents each individual association only in a distorted fashion. One feature of both SOB and C-SOB, which is at the heart of much of the models’ predictive power, is that encoding strength is determined by an item’s novelty. Novelty is assessed by computing an expectation for each incoming item, on the basis of already-encoded memories, and determining the similarity between this expectation and the actual item. The more novel the incoming item is, the more strongly it is encoded. This process of assessing novelty to determine an item’s encoding strength is termed “novelty-gated encoding.” The assumption of novelty-gated encoding has been part of SOB since its inception, and has received independent empirical support (Farrell & Lewandowsky, 2003).
Our new model, SOB-CS (CS for “complex span”), builds directly on C-SOB (Farrell, 2006; Lewandowsky & Farrell, 2008b), maintaining its original theoretical principles but slightly updating its mathematical formalization (see Electronic Supplementary Material for an explanation of these technical details). In addition, SOB-CS incorporates two further theoretical assumptions whose introduction was necessitated by the presence of distractors in the complex-span task.
First, we assume that processing a distractor, such as reading a word or carrying out an arithmetic operation, inevitably results in the encoding of a representation of the distractor into working memory in the same way as the memoranda (Oberauer & Lewandowsky, 2008). There is considerable precedent in the literature for this assumption (e.g., Logan, 1988). Therefore, distractors create interference with encoded item representations. Novelty-gated encoding applies to distractors in the same way that it applies to items, so that repeatedly processing the same distractor incurs less interference than does processing different distractors.
Second, like most models of working memory, ours assumes that the system engages in active restoration of an unimpaired memory state when time allows. This assumption is motivated by the finding that memory performance in complex span is better when distractor operations are demanded at a slower pace, leaving more free time between each distractor and the next stimulus (Barrouillet et al., 2004; Barrouillet et al., 2007). Whereas in decay-based models, active restoration typically refers to boosting decayed traces up to their original strength (by some sort of rehearsal or refreshing mechanism), active restoration must be conceptualized differently in interference-based models. When the main limiting factor for performance is interference, active restoration must reduce the impact of interference. This can be accomplished in several ways. For reasons of parsimony, we have so far implemented only one of them in SOB-CS, by applying a mechanism that is already embodied in all SOB models to date—namely, the removal of interfering material from memory, which by implication restores the quality of earlier memories. Because the removal notion is central to SOB-CS, it deserves to be placed into a broader theoretical context.
One general theoretical insight that emerged from our modeling work is that a successful model must have a mechanism for clearing working memory of no-longer-relevant contents. Without this, the system would soon be overloaded with outdated material. For example, when mentally solving an expression such as “24 × 3,” it would be inopportune to retain “3” in working memory during the final step of adding “12” to “60”—even though the concept “3” necessarily had to be brought to mind a brief moment before in order to compute “12.” In general, rapid updating of working memory would be impossible without a clearing or removal mechanism, because the system would soon be choked by proactive interference, and demonstrably, this does not happen (Kessler & Meiran, 2008; Oberauer & Vockenberg, 2009).
In decay-based models, removal of old contents from memory occurs by default (viz., they simply fade away), and active maintenance must be engaged to retain contents that are still relevant. Interference-based models operate by the reverse logic: All contents are maintained by default, and active removal is necessary to remove those that are no longer relevant. Thus, whereas decay-based models must be equipped with a mechanism for active maintenance, interference-based models must include a mechanism for active removal.
This necessary link between interference and removal has been largely ignored in the literature (for an exception, see Hasher, Zacks, & May, 1999). SOB-CS provides a precise mechanism explaining how removal is accomplished whenever there is free time in-between distractor operations—for example, during a pause between solving a distracting equation and presentation of the subsequent memorandum. During those pauses, the immediately preceding distractor representation is gradually removed from memory using Hebbian antilearning. This operation gradually undoes the association between the distractor and the position marker (see Kessler & Meiran, 2008, for the related idea of “dismantling” outdated bindings in an updating task).
The assumption of distractor removal (or “unbinding”) is a generalization of an assumption that is common in models of serial recall: Once a list item is recalled, it is removed from memory to avoid perseveration. There is strong evidence to support such a mechanism for response suppression (Farrell & Lewandowsky, 2004; Henson, 1998a), and it has been implemented in many models of serial recall (G. D. A. Brown, Preece, & Hulme, 2000; Burgess & Hitch, 1999; Page & Norris, 1998). In all versions of SOB, response suppression has been modeled using the mechanism of Hebbian antilearning. Accordingly, response suppression is an instance of removing no-longer-relevant information from memory. Here, we simply generalize this notion to distractors.
By specifying how information is removed from working memory, we flesh out one basic operation for controlling the contents of memory. Control over which information is held in working memory is being recognized as an important source of individual differences in working memory capacity (Hasher et al., 1999; Jost, Bryck, Vogel, & Mayr, 2010; Vogel, McCollough, & Machizawa, 2005). Explicitly modeling the control processes operating on the contents of working memory is a prerequisite for understanding why working memory capacity also correlates with various control processes in tasks with little involvement of memory (Kane, Conway, Hambrick, & Engle, 2007).
To summarize, strong conceptual considerations mandate the presence of some control process that can clear working memory of unwanted contents. The removal notion is supported by data and theoretical precedent, and in SOB-CS we instantiate the removal process using a mechanism of proven theoretical utility.
In SOB-CS, removal of distractors plays a role similar to that of rehearsal or refreshing of memory items in other theories. Our model does not presently include a maintenance process for the strengthening of items (e.g., rehearsal or refreshing), for three reasons. First, rehearsal or refreshing are necessary mechanisms of maintenance when memory traces are assumed to decay over time; however, in a model that attributes forgetting to interference, the threat to remembering comes from the presence of interfering material, not from the decay of memoranda, and therefore, the most effective way of protecting memory is to remove the sources of interference. Second, the existing evidence does not yield strong support for a causal role of rehearsal in complex-span tasks. While there is no doubt about the existence of articulatory rehearsal, the evidence for it being causally responsible for superior memory performance is less than compelling. For example, people who report using articulatory rehearsal in a complex-span task do not perform much better than those who report just reading the memory items as their strategy, and more effective strategies, such as elaboration, are reported by only a minority of participants (Dunlosky & Kane, 2007; Kaakinen & Hyönä, 2007). Third, as we show below, we have successfully modeled benchmark findings cited in support of refreshing without actually requiring the refreshing of memory items, and we therefore have omitted that mechanism for reasons of parsimony.
We remain open to the possibility that a rehearsal or refreshing mechanism might become necessary in a future extension of the model, if new results become available that mandate its inclusion. To summarize this crucial point: We do not claim that people do not rehearse during complex-span tasks. The existence of rehearsal is beyond dispute. We also do not rule out the possibility that rehearsal benefits memory; however, the evidence to date has turned out to be inconclusive upon closer inspection. What we demonstrate in the remainder of this article is that rehearsal is not needed to account for benchmark data in complex span.
In addition to the two new assumptions just discussed, we make explicit two hitherto tacit assumptions in SOB. First, previous versions of SOB have—for simplicity—modeled basic processes as time invariant, on the basis that in all paradigms to which the theory has been applied to date, sufficient time was available for processes to run to completion. Under those circumstances, the theory could leave temporal aspects of those processes unspecified for parsimony’s sake. By contrast, in SOB-CS, we must explicitly model the time dependence of encoding and retrieval processes because, in complex span, performance is strongly influenced by temporal parameters (Barrouillet et al., 2004). In particular, we make the uncontroversial assumption that the degree of encoding and the extent of removal of stimuli increases up to a point, as more time is available to those processes. There is considerable evidence that encoding into short-term memory takes time to be accomplished (Jolicœur & Dell’Acqua, 1998). Likewise, there is evidence that removal of information from working memory takes time (Oberauer, 2001).
Second, we make explicit the notion of a focus of attention in SOB-CS. The last stimulus encoded into working memory, or the last item manipulated, typically enjoys a privileged status of heightened availability (Garavan, 1998; McElree, 2006; Oberauer, 2003a), supporting the notion that, by default, the last representation operated upon remains in the system’s focus of attention. In SOB-CS, as in other distributed neural-network models, there is at any point in time a pattern of activation in each layer of units that (more-or-less accurately) represents an event (i.e., an item or a distractor in a specific position). We regard this currently active representation as the content of the focus of attention. The active representations in the focus of attention are those that are available for processes such as encoding (through Hebbian learning) and removal (through Hebbian antilearning, as explained below). By default, the last-presented stimulus (item or distractor), together with its serial position, is in the focus of attention, and thereby the association between that stimulus and its position can be encoded or removed.
The following sections present SOB-CS formally. To facilitate exposition, the variables used in the equations and their roles in the model are summarized in Table 1. The MATLAB model code is available as Supplementary Materials for this article.Footnote 1
Architecture and representations
SOB-CS consists of two layers of units that are fully interconnected by a weight matrix W. The item layer, with 150 units, represents items; the position layer, comprising 16 units, represents the serial positions in the current list. Items are represented by vectors of +1 and –1, constructed at random in accordance with constraints on their similarity structure. Position markers are constant vectors of values between –1 and +1, constructed such that their similarity reflects their ordinal relation. The similarity between any two position markers (expressed as their cosine) decreases exponentially with their absolute ordinal distance:
where i and j are the positions of the ith and jth items, p i and p j are vectors representing positional markers at those positions, and s p is a fixed parameter determining the degree of overlap of successive positional markers (s p = .5 throughout, as in Farrell, 2006, and Oberauer & Lewandowsky, 2008).Footnote 2
Whereas position markers are shared by all tasks requiring memory for serial order, the representations of stimuli depend on the category of items and the distractors involved in a task. We constructed representations for four categories of stimuli used in the experiments that we simulated: letters, digits, words, and generic visuospatial stimuli, each of which can serve as memory items or as distractors. For letters, we used the representations of 16 consonants (six similar and ten dissimilar) constructed by Farrell (2006) and Lewandowsky and Farrell (2008a) for use with C-SOB. The similarity structure between these 16 vectors reflects a three-dimensional multidimensional scaling solution for an empirical confusion matrix between these letters (Hull, 1973). The average similarity between consonant representations, computed as their cosine, was .65 for the similar and .50 for the dissimilar subsets.
Nine vectors were constructed to represent digits. These were created from a common prototype such that their average similarity was .50; this value reflects the fact that digits are, on average, less confusable than letters (Jacobs, 1887). Finally, we created nine sets of nine words each. The words within each set were similar to each other (cosine = .65), and words from different sets were dissimilar (cosine = .5). For simulations of experiments not manipulating similarity, we used a random mixture of similar and dissimilar letters or words for all memory lists and distractor sets. Visuospatial stimuli (used in Simulations 5 and 6) were generated in the same way as the words, except that they are represented in a separate section of the item layer.
Distractor representations were created in the same way as the item representations—that is, by sampling individual distractors from a distractor prototype. For simulations in which items and distractors came from the same broad category (i.e., digits, letters, or words), we used the same prototype for generating both items and distractors, so that the average similarity between an item and a distractor equaled that between two items and between two distractors. For simulations in which the items and distractors came from different categories, we derived the prototype of the distractors from the prototype of the items, so that they had a similarity governed by the item–distractor similarity parameter s c , which was set to .35, the same value as in previous simulations (Oberauer & Lewandowsky, 2008).Footnote 3
Encoding and recall
Figure 1 provides a schematic illustration of the encoding process in SOB-CS. Each presented memory item activates its representation in the item layer, and at the same time, the representation of the next available list position is activated in the position layer. The representations active in the item layer and the position layer jointly constitute the current focus of attention. Encoding into working memory occurs by associating the item representation with the position representation in the focus. Once associative encoding is completed, that item–position pair is replaced in the focus by the next item–position pair. Encoding uses standard Hebbian learning (see, e.g., Anderson, 1995):
Schematic illustration of encoding in SOB-CS. Top left panel: State of the weight matrix after encoding stimulus i – 1, W i–1. The new position vector p i is activated in the position layer, and its activation is forwarded through W i–1 to generate an expectation (= W i–1 p i ) for the incoming stimulus in the item layer. Activation values of the units in the position and item layers are coded by shade (white = –1, gray = 0, black = 1). A new stimulus, represented by vector v i , is initially matched against the expected vector. The degree of match is measured as energy E i . Top right panel: Energy E i is translated into the asymptote of encoding strength, A, by the logistic function, governed by free parameters e and g. Parameter e is the point on the E i scale at which A = 0.5 (illustrated by the dotted line), and parameter g determines the steepness of the function around that point. The dashed line shows the resulting A for a stimulus with E i = –300. Bottom left panel: Encoding strength η e for encoding stimulus i is computed as a negatively accelerated exponential function of the time t spent on encoding. The dotted line shows the resulting encoding strength for an item encoded for 1.5 s; the dashed line shows encoding strength for a distractor encoded for 0.3 s. Bottom right panel: Updating of the weight matrix according to the outer product of the position representation p i T and the item representation v i , multiplied by the encoding strength η e . Bold lines are the connection weights increased in this learning event because they connect units with same-signed activation. Thin lines are connection weights that are decreased because they connect units with opposite-signed activation
where W is the weight matrix connecting the position layer to the item layer, v i is the vector representing the ith presented item, and p i is the positional marker for the ith serial position, which is transposed for computing the outer product of the two vectors.
We model encoding as a time-dependent process: The encoding strength η e for the ith item, η e (i), is calculated as a function of the time spent encoding the item:
where Α(i) is the asymptote of the encoding strength of item i, R is the rate of encoding, and t e is the time spent on encoding. Thus, the encoding strength η e that determines the strength of Hebbian association is assumed to grow toward asymptote at an encoding rate of R. The asymptote itself is a function of the novelty of the incoming item, which is defined as the energy between the to-be-learned association and the information captured by W up to that point. Specifically, the asymptote A(i) for the encoding strength of item i is a logistic function of that item’s energy, E i :
where e and g are the threshold and gain parameters, respectively, of the logistic function. For all simulations, e was set to –1,000 and g to 0.0033. Simulations of simple span have shown that these values generate the highest level of memory accuracy without producing empirically unrealistic serial-position curves. The use of a logistic function smoothly restricts A(i) to fall between zero and unity, thus preventing the occurrence of implausible (e.g., <0) encoding weights. Constraining encoding strength in this way represents an improvement over previous instantiations of the model, in which the encoding strength was not bounded, without altering the basic principle of energy-gated encoding.
The energy of the ith association is given by
(see Lewandowsky & Farrell, 2008b). The computation of energy can be interpreted as the generation of an expectation for the item in position i, given the current state of memory as reflected in the state of the weight matrix before encoding of item i. The expectation is computed by cueing the weight matrix W with the new position p i . Energy is the negative dot product between the expectation (computed as Wp i ) and the actual item v i , and it reflects the degree of mismatch between the expectation and the actual item—that is, the item’s novelty. Equation 4 implies that more novel items, which have less negative (or even positive) energy values, are encoded more strongly. The use of energy to compute the weighting of incoming information is a core principle of SOB that turns out to be critical for the model’s predictions for complex span. Recent research on the processing of novelty in the hippocampus lends support to a mechanism very similar to the one assumed for SOB-CS (Kumaran & Maguire, 2007).
Our computation of encoding strength in SOB-CS differs from previous instantiations of SOB in that it makes encoding strength time-dependent. The duration of encoding an item into working memory can be estimated from dual-task studies (Jolicœur & Dell’Acqua, 1998) and from studies using masked presentation of visual stimuli (Vogel, Woodman, & Luck, 2006). These studies converge on an estimate of 150–300 ms as the average time for encoding an item into working memory. Jolicœur and Dell’Acqua applied a formal model to three of their experiments, from which we estimated the encoding rate for individual letters to be about six items per second.Footnote 4 We therefore set the encoding rate to R = 6 in Eq. 3. This value implies that η e (i) reaches 95 % of its asymptote after 500 ms. Thus, with encoding times of 500 ms or more, encoding in SOB-CS is virtually indistinguishable from encoding in previous versions of C-SOB, and Eq. 3 functionally reduces to the simple equality η e (i) = A(i) that—bar the use of a logistic squashing function—is familiar from earlier applications of C-SOB.
Retrieval proceeds by reinstating the position markers in their original order, one by one, as cues for the items with which they were associated. For position i, retrieval is cued by presenting the activation pattern for positional marker p i in the position layer and updating the activation in the item layer by forwarding activation through the weight matrix:
where the resultant vector in the item layer, v i ', is a distorted version of the original item vector v i , consisting of a blend of v i and the other item representations involved in the trial, which will all have been associated to partially overlapping positional markers. To determine which item to recall, the retrieved vector v i ' is matched to all vectors v j of known retrieval candidates in long-term memory. The similarity of v i ' to each retrieval candidate is computed as
In this equation, the Euclidean distance measure D is weighted by the free parameter c, which determines the discriminability between retrieval candidates. With larger values of c, similarity falls off more steeply with distance, so that the most similar retrieval candidate is more clearly discriminated from the less similar ones. For computational reasons, D is normalized by subtracting the minimum distance across all of the n retrieval candidates from the distance for each candidate.
The probability of recalling an item j is computed from these similarities by the Luce choice rule:
where n is the number of retrieval candidates. A candidate is then selected for recall by random sampling among the candidate set, with the probability of sampling for each candidate being determined by Eq. 8. The intact representation of the candidate selected for output, v o,i , replaces the originally retrieved vector v i ', thus placing a clearly identified retrieval candidate into the focus of attention. Figure 2 provides an illustration of retrieval in SOB-CS.
Schematic illustration of retrieval in SOB-CS. Left panel: The positional cue p i is activated in the position layer and forwards its activation through the weight matrix W to the item layer, creating an approximation of the item vector, v i ′. This vector is compared to all vectors of retrieval candidates, and their distance D(v i ′, v j ) is computed for all retrieval candidates. Right panel: Distance is converted into similarity by a Gaussian gradient. Three gradients are shown, for the three values of c used in different simulations in this article
The set of recall candidates includes not only the list items but also other items in the experimental vocabulary. This enables the model to generate extralist intrusion errors. When the distractors come from the same stimulus category as the items (e.g., both are words), we assume that the distractors are also included in the candidate set, so that intrusions of distractors in recall can be modeled. (When distractors are categorically different from the memoranda, they are excluded from the set of candidates because people can prevent intrusions on the basis of categorical information.)
Overt recall itself impairs memory for the remaining items; this effect is known as output interference (Cowan, Saults, Elliott, & Moreno, 2002; Fitzgerald & Broadbent, 1985; Oberauer, 2003b). In SOB-CS, as in C-SOB, we implemented output interference by adding Gaussian noise with a standard deviation N o to each weight in W after recall of each item.
A common assumption in models of serial recall is that recalled items are suppressed in order to avoid perseveration. Response suppression has been modeled in SOB by Hebbian antilearning (Anderson, 1991). Hebbian antilearning operates in the same way as Hebbian learning, except that a negative encoding strength is used. The negative sign implies that the association between the recalled item, v o,j , and its position is removed from the weight matrix:
where j is the output position and η s (j) is the strength of suppression at output position j.
Like Hebbian learning during encoding, Hebbian antilearning during response suppression takes time, and SOB-CS explicitly represents this. Therefore, the antilearning strength of suppression, η s (j), is a function of time:
where t s is the time devoted to response suppression of item j (set to 1s for all simulations, the approximate duration of serial recall of letters; Farrell & Lewandowsky, 2004, Exp. 2), and r is the rate of removal of representations from working memory. Ω(j) is the asymptotic value of antilearning strength, computed by a logistic function from the item’s energy:
where E j is the just-recalled item’s energy and E 1 is the energy of the item recalled at the first output position. Dividing by E 1 corrects for the overall energy of the list. That is, when more items are stored, or positional markers overlap more, the energy computed during recall will on average be higher, and dividing by E 1 effectively uses the energy of the first item to correct for this potential variability. For the first output position, a default value Ω(j) = 1 is used. The energy of the recalled item j is computed using the same formula as Eq. 5, but with the presented item replaced by the recalled item:
Distractor encoding and removal
Following our previous work (Oberauer & Lewandowsky, 2008), we assume that all distractors are associated with the position of the immediately preceding item. That item’s position is still held in the focus of attention because position representations are updated only when a new memory item is presented. Distractors are represented in the same way as items, as random vectors of –1 and +1 generated according to the category of stimuli (digits, consonants, or words), as described earlier. Processing of a distractor implies activating that distractor in the focus of attention, upon which Hebbian learning automatically associates it with the currently active position marker, using the same mechanism as for the learning of list items (Eq. 2):
where W is the weight matrix, d j,k is the vector representing distractor k following item j, p j is the position marker of position j, and η e (j, k) is the encoding strength of the distractor. The asymptotic encoding strength of the kth distractor following item j is computed, like that of an item, as a logistic function of its energy:
The energy of every distractor k following item j, E j,k , is computed as before, according to Eq. 5, using the position representation of the preceding item, p j . Because distractors are associated with positions already occupied by an item, and because all representations within a content domain are at least moderately positively correlated, distractors are typically encoded with less strength than are items, because of energy-gated encoding. Like encoding of items, encoding of distractors is a process that takes time, such that the encoding strength increases with the duration of distractor encoding, t d :
The distractor is encoded while attention is devoted to it (Phaf & Wolters, 1993). Like items, distractors reach near-asymptotic encoding strength after about 500 ms.
As noted earlier, any free time during complex-span processing is used to remove the immediately preceding distractor, using the same mechanism of Hebbian antilearning introduced above for response suppression:
where η r (j, k) is the antilearning strength for distractor d j,k , which is the kth distractor following the item in position j. Removal is a gradual process that, as compared to encoding, proceeds relatively slowly. Therefore, the strength of antilearning is computed as a function of the available free time, t f , and the asymptotic removal strength of the distractor, Ω(j, k):
where r is the rate of removal, which also governs the rate of response suppression (Eq. 10). The asymptote of removal strength is computed in the same way as the strength of response suppression:
where E 1,1 is the energy of the first distractor in the first processing episode. For the first distractor in a trial, Ω(1, 1) = 1.
Estimates from experiments in which participants were instructed to (temporarily or permanently) remove part of the contents of working memory have shown that removal takes between 1 and 2 s (Oberauer, 2001, 2002). Therefore, we set r to 1.5, which implies that the rate of antilearning for removal has reached 95 % of its asymptote Ω(j, k) after 2 s.
To summarize, SOB-CS has four fixed parameters and six free parameters (see Table 1). We regard as fixed parameters those that were treated as fixed parameters in previous versions of C-SOB and whose values we did not change; they all pertain to the similarity between representations. We regard as free parameters those that we adjusted manually—either on the basis of independent evidence, as in the case of the rate parameters for encoding and removal, or to find values that generated good model fits to the benchmark data. We set the free parameters to the same values in all simulations reported in this article, except in a few cases, which will be explicitly noted: the threshold and gain parameters of the logistic function that translates energy into encoding strength, e = –1,000 and g = 0.0033; the encoding rate, R = 6; the removal rate, r = 1.5; the confusability parameter for items during retrieval, c = 1.3; and the output interference parameter, N o = 1.5.
Before moving on to describe the application of SOB-CS to data from the complex-span paradigm, we first will briefly summarize an alternative account of complex-span performance, TBRS* (Oberauer & Lewandowsky, 2011), as that model serves as an important baseline for assessing SOB-CS’s account of several key phenomena.
An alternative theory: The time-based resource-sharing (TBRS) model
A new model must at the very least explain the data that constitute the main empirical support for extant theories and models. One contender for explaining performance in complex span is the time-based resource-sharing (TBRS) theory (Barrouillet et al., 2004), which has recently been instantiated in a computational model, TBRS* (Oberauer & Lewandowsky, 2011). TBRS* is the most sophisticated implementation yet of two popular assumptions about working memory: that memory traces decay rapidly over time, and that decay can be prevented by some form of active maintenance (i.e., rehearsal or refreshing). It is clear from the foregoing discussion that those assumptions stand in diametric opposition to the architecture of SOB-CS. Our first goal in this article is therefore to demonstrate that SOB-CS can explain the key phenomena cited in support of TBRS and TBRS* without committing to the core assumptions of the TBRS theory. Here, we summarize the TBRS theory and the key findings in its support.
The TBRS theory rests on two basic assumptions: First, forgetting is driven by time-based decay, and this decay must be offset by reactivation or refreshing of items to prevent loss of that information. Second, working memory has at its disposal a general attentional mechanism that can be devoted to only one task at a time. In the complex-span paradigm, this mechanism must engage with the distracting processing demands in-between encoding items. However, attention can rapidly switch between processing operations (e.g., carrying out an addition in an operation span task) and refreshing memory items, thereby using even small temporal gaps between individual operations to carry out refreshing. As a consequence, the model predicts that memory performance will decline with increasing time during which attention is occupied by distractor processing, and that it will improve with increasing free time that can be devoted to refreshing. These predictions can be summarized by the concept of cognitive load, defined as the proportion of available processing time between two memory items during which attention is captured by the distractor task:
with N representing the number of operations in a processing episode, a the time demand of each individual operation, and T the total time available for that processing episode. The TBRS theory predicts that memory is a monotonically declining function of increasing cognitive load, as less time is proportionally available for refreshing items. Additionally, when cognitive load is held constant, Barrouillet et al. (2004) predicted that the number of distractor operations would have no effect on memory.
To test these predictions, Barrouillet, Camos, and their colleagues developed a version of the complex-span paradigm that increases experimental control over participants’ scheduling of individual processing steps in the task (Barrouillet et al., 2004; Barrouillet et al., 2007). Following presentation of each memory item, participants work through a computer-paced sequence of processing steps (e.g., reading aloud a digit or making a speeded choice judgment). Figure 3 shows the schematic flow of events in this version of complex span. Presentation of each item is followed by a processing episode of fixed duration T, which is broken down into N processing steps. In each processing step, a relatively elementary cognitive operation is carried out on a distractor stimulus (e.g., reading a word, carrying out an arithmetic operation, or classifying a stimulus by a keypress). This operation is assumed to capture central attention for duration a. The remainder of the available time during each processing step is free time that, according to the TBRS theory, is used for refreshing memory traces.
Schematic flow of events of the complex-span paradigm of Barrouillet et al. (2004). Presentation of each memory item is followed by a processing episode that consists of a computer-paced series of distractor stimuli, each demanding a response, followed by a free-time interval until the onset of the next distractor. Operation duration refers to the time for which generation of a response to a distractor captures the central attentional mechanism, which is not directly observable but can be approximately inferred from response latencies. Cognitive load is defined as aN/T, where N is the number of distractors in a processing episode, a is the operation duration, and T is the total time
Experiments within this paradigm have revealed three consistent regularities that lend support to the cognitive-load equation: First, memory performance decreases as the pace at which processing steps are required increases (Barrouillet et al., 2004; Barrouillet et al., 2007). This effect has been found across a large variety of memory materials and distractor tasks (Hudjetz & Oberauer, 2007; Vergauwe, Barrouillet, & Camos, 2010), and with children as well as adults (Barrouillet, Gavens, Vergauwe, Gaillard, & Camos, 2009; Portrat, Camos, & Barrouillet, 2009). In terms of the cognitive-load equation, increasing the pace means increasing the ratio of aN to T by increasing N, reducing T, or both.
Second, when pace is held constant and the time demand of individual operations is increased by making the operations more difficult, memory suffers (Barrouillet et al., 2007). This is predicted by the theory because increasing the time demand a while holding the ratio of N and T constant increases cognitive load. Figure 4 illustrates the first two effects: Memory span declined as the pace of the processing task was increased, and span was lower for the processing task with longer response times overall (i.e., the parity judgment task).
Effect of cognitive load on memory span. Participants remembered consonants and carried out one of two distractor tasks (parity judgment or location judgments) that differed in their mean response times. Pace was manipulated by demanding 4, 6, and 8 judgments within a constant total time of 6.4 s. From “Time and Cognitive Load in Working Memory,” by P. Barrouillet, S. Bernardin, S. Portrat, E. Vergauwe, and V. Camos, 2007, Journal of Experimental Psychology: Learning, Memory, and Cognition, 33, pp. 570–585. Copyright 2007 by the American Psychological Association. Reproduced with permission p. 577
Third, when the pace and the time demands of individual operations are held constant, increasing the number of operations following each memory item—and, hence, the total duration for each processing episode—has often been found to leave memory performance unaffected (Barrouillet et al., 2004; Oberauer & Lewandowsky, 2008). This is predicted by the cognitive-load equation: Increasing the number of operations at a constant pace means increasing both N and T by the same proportion, so cognitive load is unchanged. This third finding, however, needs to be qualified: In a series of experiments using word reading as the distractor task, we varied the number of distractor words to be read aloud after each memory item. If the same word was repeated four times, memory was as good as when reading a single word, but when three different distractor words followed each item, additional forgetting was observed (Lewandowsky, Geiger, Morrell, & Oberauer, 2010).
In sum, the TBRS theory and its computational implementation, TBRS*, currently offer the strongest alternative account to SOB-CS for explaining key experimental results from the complex-span paradigm. We therefore regard the findings that provided initial crucial support for TBRS as the first set of benchmark results that our new model needs to explain.
Complex span: Benchmark findings and new predictions
There are no established criteria for what constitutes a benchmark finding in a field. This is an unfortunate situation, because it enables theorists to focus on those results that their preferred model handles best. To rein in this opportunistic selection of phenomena, we here state our selection criteria explicitly. We argue that benchmark findings should meet two criteria: (1) They should be theoretically informative; that is, they should count as support for, or a challenge to, the most successful theories in the field. (2) They should be robust; that is, they should be replicable across variations of theoretically unimportant features of method and materials. The findings that we selected as benchmarks for a model of complex span, summarized in Table 2, meet both of these criteria.
The benchmarks and the accompanying new predictions can be grouped into four sets. The first set consists of effects related to the interplay between short-term retention and processing, which is a longstanding topic of research and theorizing on working memory (Bayliss et al., 2003; Case et al., 1982; Towse et al., 2000). These are the effects that constitute the empirical support for the TBRS, described above. The second set consists of serial-position curves, error patterns, and transposition gradients. These are findings that, although given relatively little attention so far in the working memory literature, have been important in constraining models of serial recall. The third set pertains to the effects of similarity between memory items and distractors. These similarity effects are diagnostic for the mechanisms of interference in working memory. We test a new prediction arising from the assumptions in SOB-CS about the interference between items and distractors, and address the longstanding question of whether the disruption of immediate memory (“storage”) by distractor processing is domain-general or domain-specific. The fourth set concerns individual differences, which have been a major topic of research with the complex-span task. One of the reasons that so much interest has focused on complex span (and other working memory tasks) is that 50 % of the variance in working memory capacity across individuals is shared with measures of fluid intelligence (Conway et al., 2003). In addition, there has been considerable interest in the patterns of correlations between simple-span and complex-span tasks; we focus on those correlations because they fall within the scope of SOB-CS. In the remainder of this article, we will report the simulations through which we applied SOB-CS to these four groups of benchmark findings and present new model predictions, together with data testing them.
Cognitive load and the number of operations
The cognitive-load effect (Barrouillet et al., 2004) is an important regularity concerning the interplay between memory and processing in working memory. It implies that whereas the processing of distractors impairs memory, more generous intervals of free time between individual processing steps can be used to restore memory. The TBRS theory (Barrouillet et al., 2004) identifies decay as the cause of forgetting during processing operations, and refreshing as the beneficial force in the free intervals between operations. In contrast, SOB-CS assumes that distractor processing damages memory via the interference introduced from distractor representations entering working memory (Eqs. 13–15), and that the beneficial effect of free time arises from the gradual removal of distractor representations in-between processing steps (Eqs. 16–18).
In Simulation 1, we investigated the behavior of SOB-CS by simulating a hypothetical experiment that combined the three independent variables that have been manipulated in separate behavioral experiments to establish the first set of benchmark findings. The simulated experiment was the same as the one we used to demonstrate the feasibility of TBRS* (Oberauer & Lewandowsky, 2011, Simulation 1). The independent variables were (1) number of distractor operations per episode (zero, one, four, or eight), where zero operations defines the simple-span baseline; (2) operation duration (0.3, 0.5, or 0.7 s)—that is, the duration of attentional capture for each operation; and (3) free time following each operation (0, 0.1, 0.6, 1.2, or 2 s). Crossing of the latter two variables generated 15 levels of cognitive load, computed as operation duration divided by the sum of operation duration and free time (for a summary of the cognitive-load values, see Table 3). The simulated experiment used letters as memory items and digits as distractors, as did most of the experiments of Barrouillet et al. (2004). The simulated experiment involved 500 virtual participants, each of whom completed three trials for each list length (one to nine) in each condition.
Cognitive load
Figure 5 shows memory performance as a function of cognitive load for the four levels of number of operations (the simple-span baseline was replicated 15 times, generating one data point plotted at each level of load; the variability between these 15 identical replications provides an estimate of random noise in the simulated data). The top panel presents performance expressed as span, computed as in Barrouillet et al. (2004), and the bottom panel presents results as the proportions of items recalled in correct order for seven-item lists. Both figures show that memory accuracy declined in an approximately linear fashion with increasing cognitive load, in accordance with the data.
Results of Simulation 1. Top: Memory span as a function of cognitive load and number of distractor operations. Bottom: Proportions of correct-in-position recall as a function of cognitive load and number of operations. Dashed lines are best-fitting linear regression slopes. The 15 data points for “0 operations” are exact replications because cognitive load was not defined for that condition; their variability reflects the amount of random noise in the simulated data. The highest level of cognitive load is represented by three data points for each level of number of operations, because for all three operation durations, load = 1 when free time = 0
The span-over-load function produced by SOB-CS is not entirely linear; it contains small but systematic nonmonotonicities. These deviations from linearity can be explained by looking at the effects of the two variables that constitute cognitive load, the duration of each operation and the free time following it. Figure 6 plots span as a function of operation duration and free time (averaging conditions with one, four, and eight operations). Operation duration has only a very small effect, and hardly any effect beyond 0.5 s, because after 0.5 s the strength of distractor encoding has nearly reached asymptote. Free time has a much larger effect, albeit with diminishing returns. The comparatively small effect of operation duration explains the nonmonotonicity in the span-over-load function.Footnote 5
The results of Simulation 1 clarify how SOB-CS accounts for the first two of the three benchmark results cited in support of the TBRS theory. First, increasing the pace of processing for a fixed total processing duration decreases the free time after each distractor operation, thereby leaving less time to remove the preceding distractor. Second, increasing the duration of individual operations while holding their pace constant has two effects in SOB-CS. One is that longer attention to each distractor leads to stronger encoding, thereby creating more interference. This effect is small and levels off after 500 ms. The other, more pronounced effect is that as more of the fixed time between two operations is spent on processing the distractor, less time is left for removing it.
Unpacking cognitive load: Operation duration and free time
Cognitive load is determined by two temporal variables, the duration of distractor operations and the free time in between them. These components play different roles in SOB-CS and TBRS*. In SOB-CS, increasing the operation duration has only a limited effect through increasing the strength of encoding of interfering distractors (up to about 500 ms), whereas increasing the free time has a more pronounced beneficial effect because removal of the preceding distractor is a relatively slow process. In TBRS*, extending the operation duration leads to more decay, which continues as long as attention is captured by the operation, and extending the free time enables more refreshing of memory items. The two models differ in that SOB-CS predicts only a very small effect of operation duration if free time is held constant, whereas TBRS* predicts a much larger effect of operation duration (Oberauer & Lewandowsky, 2011, Fig. 6).
To empirically dissociate operation time and free time, we carried out three new experiments, using a method introduced by Portrat, Barrouillet, and Camos (2008). Participants remembered letters or words, and in between each pair of memoranda they carried out a size judgment task on words presented as distractors, deciding for each distractor whether the object it represented was larger or smaller than a soccer ball. Operation duration was varied between trials by selecting objects close or distant in size to a soccer ball. After each keypress indicating a decision, a predetermined free-time interval was added before display of the next distractor (i.e., the next word to be judged). The amount of free time was varied orthogonally to operation duration. These experiments are described in detail in Electronic Supplementary Material. The top panel of Fig. 7 shows correct-in-position recall accuracy. Whereas free time had a consistent and sizeable effect across all three experiments, the manipulation of operation duration had only negligible (Exps. 1 and 2) or small (Exp. 3) effects.
Top panel: Mean proportions of correct recall from three experiments varying operation duration (via difficulty: distant vs. close words) and free time (short vs. long) independently. Error bars are 95 % confidence intervals for within-subjects comparisons. Middle panel: Predictions of SOB-CS (Simulation 2). Bottom panel: Predictions of TBRS* (parameters: decay rate = 0.4, processing rate = 6, rate SD = 1.0, refreshing operation = 80 ms, retrieval threshold = 0.05, noise = 0.02)
In Simulation 2, we modeled these experiments with SOB-CS and, for comparison, with TBRS*. We used the response latencies for size judgments to estimate the operation duration (separate estimates were taken for the first operation after each memory item and for successive operations because their latencies differed substantially; see Electronic Supplementary Material). Overt response latencies do not reflect the time for which a cognitive operation captures central attention (Barrouillet et al., 2007; Pashler, 1994) because sensory and motor processing components can be carried out independently of central attention. Estimates of the duration of those noncentral processing components are consistently between 350 and 550 ms (S. D. Brown & Heathcote, 2008; Ratcliff, Thapar, & McKoon, 2004, 2010). We therefore subtracted a noncentral component of 500 ms from the measured times to obtain an estimate of central processing duration per size judgment. The noncentral 500 ms were added to the nominal free time because this time could be used to remove distractors (SOB-CS) or to refresh memory items (TBRS*). In other words, we extended the nominal free time by 500 ms and reduced the distractor-processing time by the same amount in order to reflect the likelihood that some proportion of the distractor time did not involve the attentional bottleneck. Without this assumption, both models would predict greatly exaggerated effects of free time, and TBRS* would underpredict memory performance.
Figure 7 also shows the predictions of SOB-CS (middle panel) and those of TBRS* (bottom panel). For SOB-CS, we used the default parameter values, except for the discrimination parameter c, which we raised to 2.0 to bring the predictions into the overall accuracy range of the data. For TBRS*, we also used the default parameter values (Oberauer & Lewandowsky, 2011), except for the decay rate, which we reduced from 0.5 to 0.4 to raise performance to the empirical accuracy level. The simulation results of SOB-CS confirm what we saw in Simulation 1: Free time had a relatively large effect, whereas the effect of operation duration was tiny. The simulation with TBRS* shows much larger effects of operation duration than does SOB-CS. This is because in TBRS*, longer operations lead to more decay, which results in substantial forgetting.
For a quantitative comparison of the data with the predictions of the two models, we focused on the critical effect of operation duration. Across the three experiments, the mean effect of the manipulation of operation duration (i.e., size judgment difficulty) on memory was a 2.3-percentage-point loss of performance, with a 95 % confidence interval of [0.8, 3.8]. The predicted effect from SOB-CS was 1.0 percentage points, falling inside the confidence interval of the data. The predicted effect of TBRS* was 8.6 percentage points, clearly outside the confidence interval. Therefore, the data support the unique prediction of SOB-CS that the effect of cognitive load primarily reflects a beneficial effect of free time following a distractor, whereas the duration required to process the distractor plays only a minor role.
One potential objection to our model comparison in this section is that our simulations were contingent on our estimate of the time for sensory and motor processes (500 ms), during which central attention was not occupied. With different estimates for the duration of noncentral processes, TBRS* might give a better account of the data, and SOB-CS might look worse. To investigate this issue, we ran the simulations with different values for the assumed duration of noncentral processes, ranging from an implausibly short 0.1 s to an implausibly long 0.8 s. The results of these simulations are presented in Electronic Supplementary Material; they show that, irrespective of the particular estimate of the noncentral component in the size-judgment latencies, SOB-CS gives a better account of the data than does TBRS*.
The effect of the number of operations
The third benchmark finding cited in support of the TBRS is that the number of operations in between memoranda has no effect on memory. Barrouillet et al. (2004) predicted from their model that as long as cognitive load was held constant, the number of successive distractor operations in a complex-span task should not affect memory performance. This prediction plays an important role in the TBRS theory, because it protects the theory against a challenge that other decay-based theories face. Much evidence against decay has come from studies showing that extending a distractor-filled retention interval has no effect on memory (for a review, see Lewandowsky, Oberauer, & Brown, 2009). The TBRS theory apparently escapes this challenge by predicting that the retention interval will have no effect as long as cognitive load is held constant. Therefore, it is important to examine this prediction carefully.
Simulations with TBRS* have revealed a deviation from the predictions derived by Barrouillet et al. (2004), for reasons that are intuitively obvious upon closer inspection. TBRS* predicts that memory will decline with an increasing number of operations when cognitive load is at least moderately high (Oberauer & Lewandowsky, 2011). Brief reflection reveals this prediction to be inevitable within the TBRS theory: The only circumstance under which performance can be independent of the number of operations is when the time for refreshing exactly balances the decay experienced during processing. Whenever the effect of decay is stronger than that of refreshing during an individual processing operation (and the free time following it), the TBRS theory must predict that increasing the number of operations will lead to worse memory. We confirmed this prediction by simulation with TBRS* (Oberauer & Lewandowsky, 2011). We next consider the empirical pattern involving the effects of the number of operations, before we turn to simulations of SOB-CS to investigate whether the model can reproduce that empirical pattern.
Empirically, the effect of increasing the number of operations is quite nuanced and is determined by the relationship between the successive distractors in a processing episode (Lewandowsky et al., 2010; Lewandowsky, Geiger, & Oberauer, 2008). When the distractors are all identical (e.g., “April, April, April”), saying them three or four times does not lead to more forgetting than does saying them once. In contrast, when three different distractors (e.g., “April, May, June”) follow each memory item at encoding, recall is substantially impaired relative to a single distractor. Thus, any forgetting that could be attributed to decay is turned on or off depending on properties of the stimuli that are not considered relevant by the TBRS theory.
By contrast, these effects are predicted by a key principle of the SOB model series—namely, novelty-gated encoding: After processing and encoding the first distractor, each further identical distractor has negligible novelty, and hence is encoded with negligible strength. In contrast, when successive distractors differ from one another, each of them is to some degree novel, and therefore is encoded with substantial strength, thus adding to interference. When a series of different distractors follows each memory item, SOB predicts that memory will suffer when more of them are added.
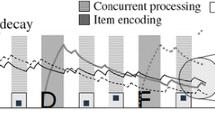
To illustrate this pattern, the top panel of Fig. 8 shows representative data from an experiment with four conditions (Lewandowsky et al., 2010, Exp. 3). The experiment involved a simple-span condition (no distractors), a condition with a single word to be read aloud after each memory item, a condition with four identical words to be read after each item, and a condition with three different words to be read after each item (four identical and three different words took an approximately equal amount of time to articulate). Participants were asked to read the distractors as quickly as possible, and the experimenter continued the sequence of events as soon as participants had finished speaking. The data in Fig. 8 show that performance dropped substantially from simple span to the condition with a single distractor, an effect that was largely additive with serial position. Reading the same word four times produced little additional forgetting; the small additional loss of memory was confined to the primacy part of the list. Reading three different words, in contrast, incurred a substantial further loss of memory. This effect was again largely additive with serial position.
Top panel: Serial-position curves for simple span (“No Distractors”) and complex span with three conditions of word reading: a single word (“1 Distractor”), the same word four times (“4 Identical”), and three different words (“3 Different”). The data are from Experiment 3 of “Turning Simple Span Into Complex Span: Time for Decay or Interference From Distractors?” by S. Lewandowsky, S. M. Geiger, D. B. Morrell, and K. Oberauer, 2010, Journal of Experimental Psychology: Learning, Memory, and Cognition, 36, pp. 958–978. Copyright 2010 by the American Psychological Association. Adapted with permission. Error bars are 95 % confidence intervals for within-subjects comparisons. Middle panel: Predictions of SOB-CS (Simulation 3). Bottom panel: Predictions of TBRS*. From “Modeling Working Memory: A Computational Implementation of the Time-Based Resource-Sharing Theory,” by K. Oberauer and S. Lewandowsky, 2011, Psychonomic Bulletin & Review, 18, pp. 10–45. Copyright 2011 by the Psychonomic Society. Reproduced with permission p. 38
The middle panel of Fig. 8 shows the results of Simulation 3, in which we applied SOB-CS to the same experimental conditions. The simulation used letters as memoranda and words as distractors to match the materials in the experiment. Representations were generated such that different words had an average similarity (i.e., vector cosine) of .5 with each other, and words overall had an average similarity of approximately .1 with the letters. Operation duration was set to 0.5 s, the value that results in near-asymptotic encoding of each distractor, in accordance with the measured word-reading latencies (>2 s for three words). Free time was set to 0.1 s to reflect the fact that there was hardly any temporal gap between the reading of successive words, as enforced by the experimenter, who urged participants to speak continuously without pauses and advanced the display sequence as soon as they had finished speaking.
With the exception of the recency effect for the single-distractor condition (which was predicted but absent in the data), the simulation closely matched the empirical data. In particular, SOB-CS accurately reproduced the interaction between number of distractor operations and distractor similarity: Increasing the number of distractors had an adverse effect on memory if and only if the distractors differed. This interaction presents a challenge for TBRS, which has no mechanisms sensitive to the similarity between distractors. This raises the question: how well could TBRS* account for the data of Experiment 3 in Lewandowsky et al. (2010) if additional assumptions were made that were particularly favorable to the model?
The bottom panel of Fig. 8 reproduces a simulation with TBRS* for that experiment (Oberauer & Lewandowsky, 2011). For this simulation, we assumed that whereas reading a new word occupies the attentional bottleneck for 0.3 s, repeating the same word does not require any further attention after the first word. Thus, cognitive load is assumed to be substantially lower in the condition with four identical than with three different distractors. It is important to realize that those assumptions are maximally favorable to TBRS*: In actual fact, reading-aloud repetitions of a word off the screen are unlikely to be completely attention-free. Only if we make this favorable assumption can TBRS* account for the relative accuracies of the four experimental conditions, averaged across serial positions. However, even under these favorable circumstances, TBRS* erroneously predicts that the effects of distractors will be entirely absent at the first list position and will increase strongly over serial positions, particularly at the last position. We will explore the reason for this erroneous prediction in the next section, when we discuss serial-position effects.
To summarize, SOB-CS correctly predicts that the effect of the number of distractor operations is modulated by the similarity of successive distractors. TBRS* can provide a post-hoc explanation for this modulation, but still it accounts for the detailed pattern of data less well than does SOB-CS.
Discussion: Cognitive load and number of operations
The strong and approximately linear relationship between memory performance and cognitive load (Barrouillet et al., 2004; Barrouillet et al., 2011) has been one of the important discoveries of the last decade in the field of working memory. There is little doubt that this function results from the interplay of two opposing processes: one that is detrimental to memory and occurs during distractor processing, and one that is beneficial to memory and occurs during brief pauses in between processing of the memoranda and distractors.
To date, the only available explanation for the cognitive-load effect has identified time-based decay and refreshing of memory traces, respectively, as those two opposing processes. This explanation lies at the core of the TBRS model. Independent evidence, however, strongly speaks against a major role of time-based decay in short-term or working memory (Lewandowsky, Oberauer, & Brown, 2009). This raises the question of whether the effect of cognitive load on immediate memory can be explained without assuming decay. Our simulations have established that SOB-CS reproduces the benchmark cognitive-load findings from complex-span tasks without invoking decay, and without invoking rehearsal or refreshing. These simulation results show that the crucial finding upon which the TBRS was built—the cognitive-load function—does not constitute unique evidence for that theory. On the contrary, when cognitive load is broken down into its two temporal components—operation duration and free time—SOB-CS arguably provides a better quantitative account of their individual effects than does TBRS*.
SOB-CS also accounts for the detailed pattern of results concerning the third benchmark, the effect of the number of operations. A previous version of C-SOB correctly predicted that under high cognitive loads, the number of operations would matter if and only if the distractors differed from each other; SOB-CS reproduced that pattern here. TBRS* can explain this finding only with the addition of favorable assumptions about variations in operation duration, and even then it mispredicts the interaction of the distractor effect with serial position.
The success of SOB-CS in modeling the first three benchmark findings lends support to the assumptions responsible for this success: Forgetting in working memory is primarily due to interference; concurrent processing adds to interference because distractor information is encoded into working memory; and the strength of distractor encoding is modulated by the distractor’s novelty, whereas free time following distractor operations can be used to reduce interference by gradually unbinding the preceding distractor from its context marker.
Inside complex span: Serial-position curves and error patterns
Our second set of empirical benchmarks involves the serial-position curve for the conventional method of scoring (i.e., recall of the correct item in the correct position), as well as for item errors and order errors within the complex-span task. SOB-CS makes two novel predictions for these benchmarks, both of which pertain to a comparison of simple to complex span. Our search of the literature revealed that the experiments of Lewandowsky et al. (2010) are the only ones that afford a controlled comparison of the serial-position curves for simple and complex span. Simulation 3 above demonstrated that SOB-CS accurately reproduces these serial-position curves. For the present discussion, we will focus on the condition without distractors (simple span) and on the condition with three different distractors following each letter, because that condition is most representative of complex-span tasks.
Serial-position curves
One prediction from SOB-CS is that the serial-position curves of simple span and complex span are largely parallel, as is shown in the middle panel of Fig. 8. This prediction is important because it distinguishes SOB-CS from models assuming decay together with rehearsal or refreshing to counteract it, such as the TBRS* model. As noted above, TBRS* predicts a strong interaction of the contrast between simple and complex span with serial position, with hardly any effect of distractor processing on recall of the first list item, and increasingly adverse effects for later list items. The reason for this prediction is that TBRS* must assume cumulative refreshing; that is, in each free-time interval, refreshing starts with the first list item. Decay models of complex span must assume cumulative rehearsal or refreshing, because decay alone imposes a strong recency gradient on memory strength (i.e., early list items decay more than later items). Cumulative refreshing, which prioritizes earlier list items, is needed to overcome this recency gradient and instead to produce a primacy effect on recall (Oberauer & Lewandowsky, 2011).Footnote 6
Cumulative refreshing largely protects the first item from decay in complex span. As cognitive load in complex span increases, refreshing progresses less far into the list (because less free time is available), but as long as cognitive load is not extremely high, the first item is always refreshed. In consequence, TBRS* must predict that the first list item is largely immune to manipulations of interference or cognitive load, but that those effects will increase across serial positions. As we noted in the introduction, any theory assuming decay needs a mechanism of rehearsal or refreshing, and therefore faces this problem.
SOB-CS does not predict this strong interaction, because it does not require cumulative refreshing to maintain a list in memory. Instead, distractor interference and distractor removal apply in the same way to each list position. As is shown in the top panel of Fig. 8, the prediction of largely parallel serial-position curves for simple and complex span was borne out by the data. This confirms the first new prediction of SOB-CS.
Item and order errors
The second new prediction concerns the relative frequencies of item errors and order errors in simple and complex span. An error is regarded as an order error if a list item is recalled in the wrong position, whereas all other errors (recalling a nonlist item or failing to recall anything and saying “pass,” if this is allowed in the experiment) are counted as item errors. An analysis of error types generated by SOB-CS in Simulation 3 showed that, whereas order errors predominate in simple span, item errors are more frequent than order errors in complex span. Figure 9 presents these predictions (top panel) and corresponding data (bottom panel) from Experiment 3 of Lewandowsky et al. (2010). As predicted, order errors were more frequent than item errors for simple span (a common finding; see Henson, Norris, Page, & Baddeley, 1996), but this relation reversed for complex span, where item errors were equally frequent at the early list positions, and were even more frequent than order errors at the later list positions. For both span tasks, order errors showed marked recency (i.e., a decline of order errors in the last output position), whereas item errors showed hardly any decline toward the end of the list. Again, this is a known pattern for simple span (Henson, 1996), and was also observed in a reanalysis of reading span and operation span data (Oberauer & Lewandowsky, 2011).Footnote 7
Item errors (intrusions) and order errors (transpositions). Top: Predictions generated by Simulation 3. Bottom: Data from Experiment 3 of Lewandowsky et al. (2010), simple span (no distractor) and complex span (three different distractors). From “Turning Simple Span Into Complex Span: Time for Decay or Interference From Distractors?” by S. Lewandowsky, S. M. Geiger, D. B. Morrell, and K. Oberauer, 2010, pp. 958–978. Copyright 2010 by the American Psychological Association
Figure 10 breaks down the order errors further by plotting the transposition gradient; that is, it shows order errors (“transpositions”) broken down by direction and distance of migration. For instance, if the item presented in List Position 4 is recalled in List Position 3, that would be an anticipation by one position (i.e., a migration of –1). Model predictions, calculated from Simulation 3, are presented in the top panel, and corresponding data from Lewandowsky et al. (2010) in the bottom panel. In both the simulated and observed data, the transposition gradients of simple and complex span are remarkably parallel. They are characterized by two effects. First, they reflect the well-known “locality constraint” (Henson et al., 1996), such that migrations become increasingly rare with larger migration distance. Second, anticipations (i.e., negative migrations) are more frequent than postponements. This is an asymmetry that has been reported before for simple span, although it is not found as consistently as the locality effect (Haberlandt, Thomas, Lawrence, & Krohn, 2005).
Transposition gradients, showing transpositions by direction and distance of migration. Top: Data generated by Simulation 3. Bottom: Data from Experiment 3 of “Turning Simple Span Into Complex Span: Time for Decay or Interference From Distractors?” by S. Lewandowsky, S. M. Geiger, D. B. Morrell, and K. Oberauer, 2010, pp. 958–978. Copyright 2010 by the American Psychological Association. Negative migrations are anticipations, and positive migrations are postponements. The values plotted are proportions of responses in each migration category, averaged across those output positions for which a given migration category is logically possible. For instance, anticipations by one position (migration = –1) are possible for Output Positions 1–4 but not for 5, because there is no item in Input Position 6. For analogous reasons, anticipations by three positions are possible only for Output Positions 1 and 2, so we averaged only across these two output positions for calculating the proportion of migrations by –3. This procedure corrects the transposition gradients for chance
In the model, the locality constraint results from the association of items to position markers, together with the overlap of neighboring position markers, which decreases over positional distance. Therefore, each position marker cues not only the item associated with it, but also items associated with neighboring positions to the degree that the position markers overlap. As a consequence, the retrieved vector is similar not only to the correct item but also, to some degree, to the neighboring items, such that close neighbors have a higher chance of being confused with the correct item than do more distant neighbors.
Discussion: Serial-position effects and error types
To conclude, SOB-CS accurately predicted detailed patterns of behavior in simple and complex span: the serial-position curve, the proportions of item and order errors as a function of serial position, and the transposition gradients. The results of these simulations confirm a number of assumptions in SOB-CS. Complex span and simple span use the same basic mechanisms for remembering lists in serial order: Items are associated with position markers that overlap as a function of their ordinal distance. In complex span, as in simple span, position markers are advanced with every new list item, not with every event (i.e., not by distractors) or by the passage of time alone. If position markers changed with every distractor, or with the passage of time (as is assumed in temporal-distinctiveness models; G. D. A. Brown, Neath, & Chater, 2007), the position markers of neighboring items would be much more dissimilar in complex span than in simple span, and the transposition gradient of complex span would be flatter.
The main difference between the two paradigms is the added interference to item representations from the superposition of distractor information in complex span. Encoding of distractors distorts the associations of memory items with their positions, thereby impairing the reconstruction of the original item from the retrieved approximation v i '. Interference from distractors does not render the retrieved item representations more similar to each other, it only makes them less similar to their original representations; this is why the distractors increase item errors more than order errors. Because distractors are associated with the preceding item’s position, each list item suffers about the same degree of distractor interference in complex span. Therefore, the effect of distractors is largely additive with serial position. As we have seen in the simulations with TBRS*, the additive effect of distractors is not easily explained in the context of models that rely on decay and cumulative rehearsal or refreshing.
Similarity between items and distractors
Interference is commonly assumed to depend on similarity between the interfering materials. Therefore, every interference model should predict similarity effects in working memory correctly. Similarity between list items is known to have a detrimental effect on serial recall, and previous versions of SOB have accounted for these similarity effects in great detail (Farrell, 2006; Farrell & Lewandowsky, 2003). We therefore do not address interitem similarity within memory lists again, but instead focus on a similarity relation that is pertinent particularly to complex span—namely, the similarity between memory items and distractors—as our third set of benchmark results.
The investigation of item–distractor similarity has a long history in memory research (e.g., Corman & Wickens, 1968; Dale & Gregory, 1966; Murray, 1967; Posner & Konick, 1966), with results that have been mixed and difficult to interpret because of the large variety of ways in which similarity has been manipulated. For our discussion, we distinguish three kinds of similarity between items and distractors. They can be explained by thinking of each item or distractor as a point in a multidimensional feature space (see Fig. 11). In distributed representations, as used by SOB-CS, each feature dimension could be represented by one unit, with different feature values coded by different activation values on that unit.
Illustration of three kinds of similarity. Each box represents the feature space (showing only two dimensions) for one representational domain. The curved line in the “verbal” feature space is a category boundary (e.g., the difference between digits and nondigit words). Items A, B, C, and D are represented as points in their feature space. The proximity in feature space between A, B, and C is about the same, but C differs categorically from A and B. Item D is a visual object that is placed in the “visual” feature space, which has different feature dimensions than the “verbal” space. Proximity between D and the verbal items is not defined, because they cannot be compared on the same feature dimensions. If D can be compared to A, B, or C on some but not all of its feature dimensions, then their feature spaces partially overlap (not shown in this figure, but see Fig. 14)
The first kind of similarity is proximity in feature space. When an item and a distractor come from the same broad category (e.g., both are words), they share the same feature space, which means that they can be meaningfully compared on the same feature dimensions. Their similarity can be evaluated as the proportions of features that they share (e.g., shared semantic features or shared rhyme), which is reflected in their proximity in feature space (see objects A and B in Fig. 11). This is the kind of similarity relation usually manipulated between memory items in simple-span paradigms.
The second kind is categorical similarity: Research on the relation between memory and distractor materials often manipulates whether they come from the same broad category. For instance, when words are used as the memory items, the distractors in the similar conditions would also be words (or sentences), and the distractors in the dissimilar condition could be digits (or equations). In this case, the items and distractors might still have a large degree of feature overlap (e.g., words and digits share many phonemes), but they would nevertheless be clearly distinct by their category membership (e.g., objects B and C in Fig. 11). This can be expressed by a category boundary in feature space.
A third kind of relation, which can also be thought of as similarity in a broad sense, is the degree of feature-space overlap. When items and distractors are from different representational domains (e.g., verbal vs. visuospatial), they cannot be meaningfully compared within the same feature space, because their features are values on different dimensions (e.g., objects A and D in Fig. 11). For instance, the question of how many features a phonological and a spatial representation share does not even arise, because spatial representations do not include phonemes, and phonological representations do not include spatial features. In what follows, we will investigate all three kinds of similarity through simulations in SOB-CS.
Proximity in feature space between items and distractors
When items and distractors come from the same stimulus category (e.g., words), similarity between items and distractors can be manipulated in the same way as similarity within lists. We recently explored this kind of similarity manipulation through simulations with SOB-CS and in a series of experiments (Oberauer, Farrell, Jarrold, Pasiecznik, & Greaves, 2012). We discovered that, under certain conditions, SOB-CS predicts better memory with higher item–distractor similarity. This similarity benefit arises if and only if the distractors immediately follow the items that they are similar to.
The item–distractor similarity benefit is a counterintuitive prediction that arises from the conjunction of two assumptions that are unique to SOB-CS: First, representations of items, distractors, and their positions are distributed, and second, each distractor is encoded by associating it with the position of the preceding item. The distributed nature of representations in SOB-CS implies interference by superposition. Each item–position association, and likewise, each distractor–position association, creates a distributed pattern of changes to the same weight matrix. Thus, all associations are superimposed, and each individual association is distorted by all others present in the weight matrix. This interference by superposition is the main cause of forgetting in SOB-CS.
An item–position association is distorted by the subsequent association of a distractor with the same position. The degree of distortion—and, hence, of interference—is larger if the pattern of weight changes induced by encoding the distractor differs substantially from the pattern of weight changes induced by encoding the preceding item. If a distractor following an item is similar to that item, it induces a pattern of weight changes that is largely congruent with the item–position association, distorting it less than does a distractor that is dissimilar to the item. This is illustrated in Fig. 12. For this reason, SOB-CS predicts that interference from distractors in complex span is less severe if the distractors are similar to the immediately preceding items. No such similarity benefit is predicted in case distractors are similar to the items following them. The reason for this asymmetry is that in SOB-CS, distractors are associated but this relation reversed for complex span, where with the position of the preceding item, so it is their similarity to the preceding item that matters, and they have a diminished effect on the subsequent encoding of items that are associated with a different context marker.
Illustration of the beneficial effect of item–distractor similarity through superposition in the weight matrix. The state after encoding the item v i is shown at the top. To the left is the situation in which a similar distractor following that item is associated with the same position p i . The weight matrix is changed (strengthened connections become bolder, weakened ones thinner) by superimposing the distractor–position association upon the item–position association (and all previously encoded associations). This change does not seriously distort the pattern of connection weights. On the right, a dissimilar distractor is instead associated with the same position, distorting the weight matrix toward a diffuse pattern. At retrieval (bottom row), a vector similar to the original item v i is retrieved on the left, but a more blurred vector that is less similar to the original is retrieved on the right
We tested these predictions with four experiments manipulating the phonological similarity between nonword items and nonword distractors (Oberauer et al., 2012). Each memorandum was followed by two distractors to be read aloud. In the similar-following condition, each item was followed by two distractors similar to it. Using capital letters for memoranda and lowercase letters for distractors, such a sequence would be AaaBbbCccDdd, with each letter denoting a set of similar nonwords. In the similar-preceding condition, the items and distractors were still similar to each other, but the distractors were followed by the items similar to them: AbbBccCddDaa. In the control condition, the items and distractors were dissimilar throughout: AeeBffCggDhh.
Figure 13 shows the predictions from SOB-CS (left panels) and the data (right panels) from the similar-following condition (top) and the similar-preceding condition (bottom), each paired with a control condition. The experiments confirmed the model’s prediction that similarity enhances recall in the similarity-following condition but not in the similarity-preceding condition (Oberauer et al., 2012). In addition, a detailed analysis of distractor intrusions (not reproduced here) showed that distractors tended to intrude in the list position of the immediately preceding item, as predicted from the assumption that distractors are associated with the position of the preceding item. In addition, recall of a distractor in place of an item was more likely if that distractor was similar to the item. Thus, high item–distractor similarity increases the chance of one particular kind of error, even when it leads to better recall overall. This pattern is precisely as predicted by SOB-CS (Oberauer et al., 2012). It reflects two kinds of interference occurring in SOB-CS, which are affected in opposite ways by similarity: High similarity (i.e., proximity in feature space) increases the chance of confusion between representations, if they are both recall candidates. At the same time, high similarity also reduces interference by superposition if both representations are associated with the same positional context.
Serial-position curves for reconstruction of lists of nonwords combined with similar or dissimilar nonword distractors. Top: Distractors follow the items that they are similar to. Bottom: Distractors precede the items that they are similar to. Predictions from Simulation 8 are on the left; experimental data are on the right (with error bars reflecting 95 % confidence intervals for within-subjects comparisons). They are from Oberauer et al. (2012), p. 9 (our top row of figures) and p. 13 (bottom row)
Categorical similarity between items and distractors
Categorical similarity of items and distractors is varied when items and distractors are drawn from the same versus from two different categories. For instance, Turner and Engle (1989) created four versions of complex span by combining memory lists of words or of digits with distractor tasks involving words (reading sentences) or involving digits (verifying equations). Memory was worse for the combinations in which the items and distractors came from the same category. Conlin, Gathercole, and Adams (2005) replicated this pattern. These data show that whereas high feature-space proximity of items and distractors within a category is neutral or even helpful for memory, as discussed in the immediately preceding section (Oberauer et al., 2012), high categorical similarity between them is detrimental.
SOB-CS treats these two forms of item–distractor similarity differently. When distractors come from a different category than the items and people represent them as such (such that they are separated by a represented category boundary), we assume that people exclude the distractors from the set of recall candidates. Even if the representation retrieved at a given position were very blurry, people would not report a digit if they knew that all of the memoranda were words; the category boundary prevents interference by confusion. Therefore, in our simulations we included the distractors in the candidate set if and only if they came from the same stimulus category as the items (with digits, letters, and words constituting the three available categories for verbal materials). These categories are so clearly distinct that people arguably represent them as such, and this enables them to exclude distractors from the candidate set if they come from a different category than the memoranda. As a consequence, item–distractor combinations from the same stimulus category are disadvantaged because of an increased chance of intrusion errors from the distractor set. Simulation 4 involved the four combinations of Turner and Engle (1989). We simulated recall of six-item lists with four operations after each item at an intermediate level of cognitive load (0.5 s of operation duration, followed by 0.5 s of free time). The mean accuracy for recalling digits was .75 when digits were used as the distractors, but it increased to .80 when the distractors were words. In contrast, the mean accuracy for recalling words was .52 with digit distractors, which fell to .46 when words were used as the distractors. Thus, SOB-CS reproduces the finding that memory is worse when the distractors come from the same broad category as the items.
Feature-space overlap between items and distractors
One longstanding question in working memory research has been whether working memory is a unitary system or should be conceived of as fractionated into separate, domain-specific subsystems. Much research along these lines has been guided by Baddeley’s (1986) tripartite model of working memory that proposes different subsystems for verbal (in particular, phonological) and visuospatial maintenance. Numerous studies have been conducted in search of double dissociations between verbal (including numerical) and visuospatial working memory with dual-task combinations that cross the content domain of the primary task (verbal vs. visuospatial) with that of the secondary task (see Jarrold, Tam, Baddeley, & Harvey, 2011).
We focus here only on those studies that have investigated complex-span performance with verbal and with visuospatial memory items, combining each with either verbal or visuospatial distractor tasks. The results have been mixed. Some experiments have found that distractor processing in the same domain impaired memory, whereas distractor processing in the other domain had no effect on memory at all (Hale, Myerson, Rhee, Weiss, & Abrams, 1996; Myerson, Hale, Rhee, & Jenkins, 1999), or had a substantially reduced effect (Chein, Moore, & Conway, 2011; Shah & Miyake, 1996). Other researchers have found only partial dissociations, such that verbal memory was impaired more by verbal than by visuospatial processing, but visuospatial memory was impaired approximately equally by processing in both domains (Bayliss et al., 2003; Vergauwe et al., 2010).
Different representational domains can be characterized as separate feature spaces (illustrated by the rectangular and diamond-shaped spaces in Fig. 11), which are implemented in distributed neural networks such as SOB-CS as nonoverlapping sets of units in the item layer. When items and distractors have no shared feature dimensions (i.e., are represented by nonoverlapping feature spaces), they differ in similarity in a different way than when they have no shared features (i.e., they have low proximity within a feature space). Two phonologically very dissimilar words might share no features but still be located in the same feature space. They are represented as different patterns across the same set of units in the item layer, such that they distort each other when superimposed. In contrast, a phonological representation of a word and a visuospatial representation of orientation cannot even be compared on any shared feature dimension. Instead they are represented as patterns across nonoverlapping sets of units, and therefore don’t interfere with each other.
Thus, if the representations involved in the processing activity of a complex-span task are from a domain entirely different from that of the memory items, SOB-CS predicts no interference between them. The problem with evaluating this strong prediction against the existing data is that we cannot be confident that a nominally visuospatial processing task involves only visual or spatial representations, and that a nominally verbal task involves only verbal representations, for at least four reasons.
First, some of the distractor tasks used in complex span require processing of both verbal and visuospatial information. For instance, the verbal processing task of Bayliss et al. (2003) involved searching a visual display for an object whose color matched that of an object named verbally. Even an easy search task such as theirs involves moving attention in space and processing the objects’ colors, thus generating spatial and visual representations. Second, the presentation and response modalities of nominally verbal processing tasks often involve visual and spatial features. For instance, word reading involves processing of the visual word form; sentence reading in addition involves eye movements. Distractor tasks often require manual responses to keys distinguished by their spatial locations (e.g., Vergauwe et al., 2010). Both eye movements and limb movements to spatial targets are known to disrupt spatial working memory (Lawrence, Myerson, Oonk, & Abrams, 2001). Third, it is usually not known to what degree people maintain in working memory a verbal representation of the task instruction for a nominally visuospatial processing task. For instance, the processing component of complex-span tasks sometimes involves choice tasks with arbitrary stimulus–response mappings (e.g., Vergauwe et al., 2010), and participants might use verbal self-instruction to remind themselves of which response key belongs to which stimulus category. Verbal self-instruction has also been shown to assist in task switching (Emerson & Miyake, 2003; Kray, Eber, & Karbach, 2008), and the complex-span paradigm requires frequent switches between encoding of memory items and working on the processing component. Finally, representations of memory items are often not domain-pure. Visual and spatial stimuli are often encoded in verbal format (e.g., by describing the position of a dot in a matrix as “middle-left”). Verbal items (in particular, words) are often represented semantically, and the meanings of many words are suffused with spatial aspects, both literally and metaphorically (Bar-Anan, Liberman, Trope, & Algom, 2007; Lakoff & Johnson, 1980). This impurity of stimulus representations can also apply to the stimuli involved in the processing task.
Accordingly, there are numerous reasons to believe that a nominally verbal processing task does not involve purely verbal representations, and that a nominally visuospatial task does not involve purely visual or spatial representations. Therefore, the strong prediction of SOB-CS that processing tasks from a different representational domain should not interfere at all with memory is very difficult to test in practice. Realistically, for most experiments we can only make the weaker prediction that processing tasks should interfere more with memory items in the same domain than with memory items in a different domain. On balance, the extant evidence summarized above is consistent with that prediction: There is some cross-domain interference, but it is weaker than within-domain interference (Jarrold et al., 2011).
In SOB-CS, we model tasks involving stimuli from both verbal and nonverbal (e.g., visuospatial) domains by extending the item layer, as illustrated in Fig. 14. Assuming that the original 150 units of the item layer serve to hold verbal representations, a second set of 150 units is added to the item layer to hold visuospatial representations. Purely verbal representations would be vectors with nonzero values in the first 150 units and zeros in the remaining units; purely visuospatial representations would have nonzero values only in the second set of 150 units. In our simulations, we allowed for a variable degree of domain impurity in the representations of memory items and distractors. This impurity was implemented by shifting the representations toward the middle of the item layer, so that a visuospatial representation would invade the verbal section to some degree, and vice versa (see Fig. 14).
Extended architecture of SOB-CS, with an item layer covering both verbal (first 150 units) and visuospatial (second 150 units) representations. The whole item layer is connected by a weight matrix to the position layer, so that verbal and visuospatial contents are associated with the same position representations by different subsets of the weight matrix (marked by horizontal–vertical shading for the verbal subset and diagonal shading for the visuospatial subset). Representations involved in nominally “visuospatial” tasks are assumed to contain variable amounts of verbal contents, thus recruiting a variable proportion of verbal units, and vice versa. The figure illustrates the representation of a nominally visuospatial distractor by a vector of 150 nonzero values, projected primarily over the visuospatial units but shifted slightly into the verbal domain of the item layer. As a consequence, weight changes imposed by encoding the distractor affect part of the verbal section of the weight matrix (dark shading), thus creating interference with verbal memory items
Simulation 5 served to investigate the interference between memory items and distractors from different domains under the assumption of different proportions of shared feature dimensions. The simulation used a design similar to that of Simulation 1, testing memory span for the same 15 levels of cognitive load but holding the number of operations constant at four. The memory items were letters; for simplicity and consistency with the preceding simulations, we assumed purely verbal representations for the letters. The distractors were modeled as primarily visuospatial representations, with their degree of impurity (i.e., overlap with the verbal section of the item layer) varied over six levels: 0, 5, 10, 20, 30, and 50 percent of the 150 units of the verbal section were recruited for the distractor representations.
The resulting span-over-load functions for different proportions of overlap are displayed in Fig. 15. They show that, with no or very low overlap, distractors from a different domain do not interfere with memory—as reflected in the flat cognitive load function when the overlap is 0 %—whereas with increasing overlap, the span-over-load functions become steeper, approaching the degree of interference obtained with distractors from the same domain (see the predictions for four operations in the upper panel of Fig. 5).
We conclude that SOB-CS can explain the occasional finding of cross-domain interference between memory and processing by assuming some degree of task impurity. Specifically, SOB-CS can explain the results of Vergauwe et al. (2010), who demonstrated cross-domain interference that increases linearly with cognitive load; this is shown in the declining span-over-load curves in Fig. 15. At the same time, the model can also reproduce the double dissociation of verbal and visuospatial working memory: With less-than-perfect overlap of feature dimensions, cross-domain interference is smaller than within-domain interference, as can be seen by comparing Fig. 15 to Fig. 5. With no overlap, there is no cross-domain interference at all. Thus, SOB-CS can explain the main experimental evidence for the distinction of domain-specific subsystems in working memory. SOB-CS does not require such domain-specific subsystems, it only requires the straightforward assumption that entities in different domains are represented in different feature spaces, such that their representations use different sets of units.
Discussion: Variety of item–distractor similarity
To summarize, SOB-CS accounts for the effects of three kinds of similarity (or dissimilarity) between items and distractors (see Fig. 11). The most radical form of dissimilarity is a change of content domain. When distractors come from a different content domain from that of the items, their representations use only partially overlapping sets of units, and therefore interference between them will be reduced and, in extreme cases of no overlap, eliminated. In this way, SOB-CS explains the frequently observed double dissociation between verbal and visuospatial working memory tests without assuming separate subsystems.
A second form of dissimilarity, combining items and distractors from different categories within a content domain, also reduces the amount of interference, because it facilitates exclusion of distractors from the set of recall candidates.
Whereas the first two kinds of similarity increase interference, SOB-CS predicts that the third kind, proximity between items and distractors within the same feature space, reduces interference under some conditions. Our experiments (Oberauer et al., 2012) have confirmed this counterintuitive prediction, lending strong support to the assumptions about item–distractor interference in SOB-CS.
To understand the effects of the three kinds of similarity on memory, it is important to consider how they modulate the two kinds of interference in SOB-CS: interference from superposition and interference by confusion. Interference from superposition determines how much the retrieved vector v i ' is distorted relative to the vector v i representing the originally encoded stimulus. The extent of mutual distortion of two representations is larger, the more that their feature spaces overlap. Within the feature space they have in common, however, higher similarity (i.e., higher proximity) implies less distortion.
The second form of interference occurs through confusion of the correct item with another recall candidate. This occurs when the retrieved vector v i ' is compared to all recall candidates. The chance of interference by confusion depends on which elements are included in the candidate set; this is why excluding distractors from a different category than the memoranda improves complex-span performance. The probability of confusion also increases with the proximity among the candidates in feature space. Thus, proximity in feature space has two opposing effects: It reduces the degree of interference from superposition, and it increases the chance of interference by confusion. Both effects were shown in experiments in which we varied the phonological similarity of items and distractors (Oberauer et al., 2012): Higher similarity improved memory overall, but also led to a specific increase of intrusions from distractors replacing the items that they were similar to.
Individual differences
Much of the appeal of the complex-span paradigm comes from its impressive success as a tool for assessing working memory capacity as an individual-differences variable, both within an age group (Conway et al., 2005; Engle, Tuholski, Laughlin, & Conway, 1999; Kane, Bleckley, Conway, & Engle, 2001) and across age groups at both ends of the life span (Bayliss, Jarrold, Baddeley, Gunn, & Leigh, 2005; Gathercole, Pickering, Ambridge, & Wearing, 2004; J. McCabe & Hartman, 2003). Our final simulation thus addressed individual differences in simple- and complex-span performance.
Findings from correlational studies with span tasks can be grouped into two sets: those concerning correlations between different kinds of simple and complex span, and those concerning correlations of span tasks to external criteria, such as measures of intelligence or academic achievement, or to experimental tasks measuring various cognitive constructs. The latter set, though undoubtedly theoretically highly relevant, are currently outside the scope of our modeling, because modeling these relationships would require modeling not only the span task but also the external criteria (e.g., performance on intelligence tests). Therefore, we will focus here on the first group of findings.
Within our chosen set, two phenomena are well established: First, complex-span tasks and simple-span tasks load on separate but correlated factors (Bayliss et al., 2003; Conway, Cowan, Bunting, Therriault, & Minkoff, 2002; Gathercole et al., 2004; Kane et al., 2004). Second, when span tasks with contents from different domains (i.e., verbal–numerical vs. visuospatial) are used, they load on separate but highly correlated factors. Both of these benchmark findings are reflected in the largest existing data set on the factor structure of span tasks, the study by Kane et al. (2004). We therefore used the factor structure in their study, reproduced in the top panel of Fig. 16, as the target for Simulation 6.
Factor structure of simple and complex span. The top figure is reproduced with permission from the original article of Kane et al. (2004) Top: Measurement model of Kane et al. (2004). Bottom: Measurement model applied to the data of Simulation 5 [fit of the measurement model: χ 2(48) = 62.1, CFI = .998, RMSEA = .012, SRMR = .014]. WMC = working memory capacity, reflecting complex span (Cspan); STM = short-term memory capacity, reflecting simple span (Sspan); V = verbal (including numerical), S = spatial. Numbers are standardized parameters; correlations between the factors are shown on the correlation paths; loadings of the manifest variables on the factors are shown alongside the manifest variables. Error terms are omitted for simplicity
One noteworthy feature of the four-factor structure of Kane et al. is that the two complex-span factors are more closely correlated (.83) than are the two simple-span factors (.63). This pattern has also been observed in a large correlational study of working memory in children (Alloway, Gathercole, & Pickering, 2006). This finding can be interpreted as reflecting a domain-general source of variance that affects complex span more strongly than simple span.
In computational models such as SOB-CS, individual differences in task performance arise naturally from individual differences in parameter values. In Simulation 6, we introduced variance across the simulated subjects in the c parameter (which determines the discriminability between retrieval candidates) and the r parameter (removal rate). We chose differences in c as a source of variance shared between simple and complex span but specific to each content domain, because it is plausible that the discriminability of representations in the set of recall candidates is domain specific: Individuals might have highly distinct verbal representations but less distinct visuospatial representations, or the other way around. Therefore, we assumed two uncorrelated c parameters, one for verbal and one for spatial span tasks.
We chose differences in the removal rate r as a source of variance that plays a larger role in complex than in simple span, and thereby accounts for the distinction between complex-span and simple-span measures. Recall that in complex span, removal affects all distractors as well as list items after their recall, whereas in simple span, removal is limited to postrecall response suppression.
Simulation 6 reproduced the design of Kane et al. (2004), crossing content domain (verbal–numerical vs. visuospatial) with span type (simple vs. complex), representing each design cell with three independent tasks. We created a normal distribution of parameter values across subjects (N = 2,000), adding Gaussian noise with a mean of zero and a standard deviation of 0.15 to the c parameter, and adding Gaussian noise with a mean of zero and a standard deviation of 0.5 to the r parameter. Two uncorrelated distributions of c were created in that way, one for the six verbal span tasks and one for the six visuospatial span tasks. A single distribution of r applied to all tasks. The means of c and r, as well as the values of all other parameters, were the same as in Simulation 1.
The complex-span tasks of Kane et al. (2004) differed in the processing tasks that they involved, and little information is available about the operation durations and free time in these tasks. For simplicity, we used the same time values for all six complex-span tasks, assuming intermediate values (i.e., 0.5 s operation duration followed by 0.5 s free time). Each complex-span task involved four operations following each item.
The three span tasks in each design cell (e.g., the three verbal complex spans) were simulated as three independent replications with the same parameter values for each subject; they differed only in the stimulus sets, which were generated anew for each task, and the random noise introduced by output interference. The tasks from different content domains in addition differed by the individual parameter values of the distinctiveness parameter c. As in Kane et al. (2004), each subject completed three trials of each memory-set size for each task; whereas in the original study the range of set sizes was calibrated to each task’s difficulty, in the simulation we ran all set sizes from one to nine for all tasks. Performance was scored, as in Kane et al. (2004), by calculating the proportions of items recalled in correct position, averaged across all trials of each task.
The bottom panel of Fig. 16 shows the results of fitting a four-factor structural-equation model to the simulated data. The model gave an excellent fit for the data, χ 2(48) = 62.1, CFI = .998, RMSEA = .012, SRMR = .014. Simulation 6 reproduced the key results of Kane et al. (2004): Spans from different content domains loaded on separate but substantially correlated factors. Within each domain, complex-span factors were separate from, but highly correlated with, those for simple span. This correlation was driven by the shared variance of c. The cross-domain correlation was larger for complex than for simple span. Because the c parameters for the verbal and spatial tasks were uncorrelated, the positive correlation across domains could only come from variations in r. The removal parameter r had a larger effect on cross-domain correlations in complex span than on those in simple span, because in simple span it only governed the effectiveness of response suppression, whereas in complex span it also governed the effectiveness of distractor removal.
Simulation 6 demonstrated that SOB-CS can reproduce benchmark findings from individual-differences studies concerning the factorial structure of span tasks. The simulation showed that variation in two model parameters—the discriminability of representations in the recall candidate set, c, and the rate of removal, r—was sufficient to generate the benchmark pattern of correlations. We do not claim that variations in this particular pair of the parameters are uniquely necessary to explain the data.
Evidence for a role of the distractor removal parameter r in explaining individual differences in complex span comes from a study by Carretti, Cornoldi, De Beni, and Palladino (2004). They used a version of complex span in which, on each trial, participants listened to several short word lists, remembering the last word of each list. Whenever participants heard an animal word, they had to tap on the table. At recall of the list-final words, people made more intrusions of animal than of nonanimal distractors (replicating a previous finding by De Beni, Palladino, Pazzaglia, & Cornoldi, 1998). Animal-distractor intrusions were specifically increased in people with low working memory capacity. Low-capacity participants also showed a larger priming effect for the complex-span distractors in a subsequent lexical decision task, and a larger latency advantage for accepting animal distractors in a recognition test, when these tests were carried out right after a complex-span trial. These findings show that individual differences in how strongly distractors remain in working memory at the end of a trial are related to individual differences in capacity, as would be expected if individual differences in the efficiency of removing distractors (parameter r) were in part responsible for variation in measures of working memory capacity.
General discussion
Working memory is one of the core constructs of cognitive psychology. So far, theorizing in the field has primarily involved the verbal description of components and mechanisms. Our goal for this article was to apply the conceptual rigor of computational modeling of serial-recall tasks to complex span, one of the major paradigms for studying working memory. This computational approach is embodied in our interference model of working memory, SOB-CS. We now discuss the key assumptions of the new model, its limitations, its relations to other theories, and the most important theoretical conclusions from our work.
New assumptions in SOB-CS: Distractor encoding and removal
Our new model, SOB-CS, introduces two assumptions that go beyond existing theories and models of working memory.
The first new assumption is that distractors create interference by being encoded into working memory. In particular, distractors are associated with the position of the immediately preceding item, using the same mechanisms as item encoding. This assumption is motivated by a host of findings showing that memory encoding is an obligatory byproduct of processing (Craik & Lockhart, 1972; Hyde & Jenkins, 1969; Logan, 1988). In the field of immediate recall, Phaf and Wolters (1993) provided direct evidence that distractor words spoken aloud are incidentally encoded into memory to the degree that they attract attention (see also Aldridge, Garcia, & Mena, 1987). Therefore, we assumed that the strength of distractor encoding is a function of how long attention is devoted to processing them, as well as of the novelty of the distractor. Evidence for the fact that distractors are associated with the immediately preceding item’s position marker comes from our finding that, when distractors intrude into recall, they are more likely to replace the immediately preceding item than another list item (Oberauer et al., 2012).
The second new assumption in SOB-CS is particularly novel and unique. During the free-time interval following encoding of a distractor, that distractor’s association with the currently focused position is gradually removed from memory. This assumption is supported by three lines of reasoning. First, distractor removal is a natural extension of the mechanism of response suppression in SOB, a process for which there is strong evidence. For example, people are very unlikely to commit repetition errors, even if lists contain repeated items (Duncan & Lewandowsky, 2005; Henson, 1998a; Jahnke, 1969). Our assumption in SOB-CS simply generalizes the rationale and the already-existing mechanism of response suppression: Representations that are no longer relevant are removed by Hebbian antilearning. Thus, similar to the way in which a just-recalled item is suppressed because it has become irrelevant, the just-processed distractor is removed by an identical process because it, too, has become irrelevant.
Second, removal of no-longer-relevant contents is a necessary mechanism for a functioning working memory system that does not rely on decay. Hasher, Zacks, and their colleagues have argued that removal (in their terms, “deletion”) of irrelevant working memory contents is one of the inhibitory functions that becomes deficient as we reach old age, and as a consequence, working memory becomes cluttered and is rendered inefficient (Hasher & Zacks, 1988; Hasher et al., 1999). Direct evidence for the removal of irrelevant subsets of memory items comes from experiments in which people encoded two sets of digits or words and were then informed which of them was (temporarily or permanently) irrelevant for the upcoming task. The effect of the number of items in the irrelevant set on latencies for accessing elements from the remaining set diminished gradually over the time, disappearing 1–2 s after the cue (Oberauer, 2001, 2002, 2005b). The time course of the vanishing irrelevant set-size effect guided our decision to set the removal rate parameter r to a value according to which removal was nearly complete after 2 s. A neuroimaging study with the same paradigm showed that the neural activity associated with the irrelevant set rapidly declines to baseline shortly after the cue and reemerges when the same set is cued as relevant later, directly demonstrating flexible control of the contents of working memory (Lewis-Peacock, Drysdale, Oberauer, & Postle, 2011).
Third, independent evidence has emerged for the notion that selective removal is an active process that not only takes time but also competes with other processes. Fawcett and Taylor (2008) combined an item-wise directed-forgetting paradigm with detection of a visual probe as a secondary task. The visual probe appeared at variable intervals after the cue, which indicated for each item whether it should be remembered or forgotten. Response times to the visual probe were delayed more after a forget cue than after a remember cue, demonstrating that forgetting is an active process that delays response to an attention-demanding secondary task. This effect was obtained only at delays of less than 2 s after the cue, in agreement with our estimate that removing a representation from memory is completed after about 2 s. Wylie, Foxe, and Taylor (2007) added further evidence that instructed forgetting of a just-encoded item is an active process that recruits brain regions not involved in active remembering or in unintended forgetting. These findings provide evidence that removal of irrelevant information is different from selective maintenance of relevant information, and they point to the fact that an attentional bottleneck is necessary for the removal of information.
Distractor removal in SOB-CS takes the beneficial role that in other theories of working memory is taken by rehearsal or refreshing. For instance, in the TBRS theory, free time following a distractor operation is used to refresh memory items, and refreshing is a crucial component of how the TBRS theory explains the cognitive-load effect. In contrast, SOB-CS does not invoke rehearsal or refreshing to explain any of the benchmark findings.
The present authors differ in the extents to which they believe that rehearsal or refreshing plays a role for maintenance in working memory. So far, we have not implemented these processes in SOB-CS for two reasons. The first and most obvious reason is that a restoration process is not needed to explain the benchmark findings modeled here. We have demonstrated that the cognitive-load effect, one important piece of evidence cited in support of refreshing, can be explained without appeal to that mechanism. The second reason is that rehearsal or refreshing is not easily integrated with the other mechanisms of SOB-CS. Rehearsal or refreshing in its simplest form would mean that items are retrieved, using a position cue, and then reencoded by associating them again with the same position cue. Such a mechanism would be fairly ineffectual, because encoding an item for a second time in the same position is dampened by novelty gating. The expected increase in memory strength therefore would be minor, at best. This small expected gain stands against a substantial risk: If the wrong item were retrieved in a given position, the wrong item would be encoded in that position, and because that item was encoded in that position for the first time, it would be encoded fairly strongly, thus creating substantial interference. In sum, in the context of SOB-CS, there is little to gain and much to lose from such a mechanism of rehearsal or refreshing.Footnote 8
That said, we must underscore that we do not rule out a role for rehearsal in working memory. It is abundantly clear that people do rehearse; a substantial proportion of people, when asked about their strategies on complex-span tasks, report some form of rehearsal. About one third of participants report repeating the memory items to themselves as their main strategy, whereas another third report using no strategy except for reading the memoranda. The final third of participants report more elaborate strategies, such as generating visual images for the to-be-remembered words or trying to combine the words into sentences (Bailey, Dunlosky, & Kane, 2008; Dunlosky & Kane, 2007). Thus, rehearsal as a behavioral phenomenon is well established, and we do not question its occurrence. Nonetheless, our simulations show that rehearsal is not necessary as a causal explanatory construct to account for complex-span performance. New data or other data not yet addressed by SOB-CS may eventually require the addition of such a mechanism (e.g., Jarrold, Tam, Baddeley, & Harvey, 2010).
In this context, it is illuminating that the performance of those individuals who report rehearsal by repetition is hardly better than the performance of people who report merely reading the items as they are presented, lending support to our contention that rote rehearsal is not needed to explain memory performance in complex span. Unlike rote rehearsal, more elaborate strategies are associated with better performance (Dunlosky & Kane, 2007; Kaakinen & Hyönä, 2007). This pattern of results meshes well with the earlier analysis that mere retrieval and reencoding of items is bound to be fairly ineffective in SOB-CS. Exploring the possibility that elaborative rehearsal might prove more successful in the model is a task for the future.
In contrast to rehearsal, removal of distractors has not figured prominently in self-reported strategies. We do not regard this as problematic for our model. One trivial explanation could be that no researcher ever considered the need for active removal. However, we believe that there is more to this conspicuous absence. Removal is unlikely to be the subject of self-reports because people report cognitive processes to the extent that they pay attention to them and remember them. Removing a no-longer relevant representation implies that it fades from the focus of attention and vanishes from working memory. By removing distractors, increasingly clean and distinct representations of the memory items emerge, which then have an increasing chance to be remembered later, not only when it comes to recalling the items, but also when it comes to reconstructing a memory of one’s own strategy. When asked what they did during a complex-span trial, participants will remember that, after processing a distractor, their attention eventually switched away from that distractor and to one or more of the items. The experience of this transition, which we argue is facilitated by removal of the distractors, can plausibly be described by participants as “refreshing the items” or “rehearsal.” The more efficient a person is in removing distractors from memory, the more rapidly and clearly the memory of the items would emerge from the fog of interference, and the more opportunity the person would then have to engage in further elaborative processes, such as visualizing the meanings of words or creating sentences from the words. Thus, faster distractor removal might be the common cause of better memory and of more elaborate processing of the items.
Limitations
SOB-CS is an attempt to formulate a precise and empirically adequate model of one particularly popular and fruitful experimental paradigm of working memory research. Modeling complex span is clearly a necessary part of what it means to model working memory. At the same time, we recognize that it is only a small part of the theoretical and empirical landscape.
Computational models that spell out assumptions about representations and processes in as much detail as SOB are often limited to a single experimental paradigm, such as immediate serial recall. With the development of SOB-CS, we are generalizing the model, extending it from simple span to complex span. Nonetheless, to become a complete model of working memory, SOB-CS will have to be extended further to account for behavior on other prototypical working memory tasks, such as the Brown–Peterson paradigm and variations thereof (J. Brown, 1958; Jarrold et al., 2010; Peterson & Peterson, 1959) and memory-updating tasks (Ecker, Lewandowsky, Oberauer, & Chee, 2010; Pollack, Johnson, & Knaff, 1959; Yntema & Mueser, 1962). The model also needs to be extended to other response formats beyond serial recall and reconstruction, such as free recall (Bhatarah, Ward, & Tan, 2008; Farrell, 2012), probed recall (Tehan & Humphreys, 1995), and recognition (McElree, 2001; Oberauer, 2005a). We believe that the model is well suited for at least some of these extensions. For instance, updating of working memory requires efficient, targeted removal of representations that must be replaced (cf. Kessler & Meiran, 2008); SOB-CS already includes such a mechanism. Recognition requires a quick assessment of the familiarity of a probe; the computation of energy in SOB-CS offers a potential mechanism.
SOB-CS is also limited in that it does not make explicit how working memory relates to long-term memory. We are not committed to a strong distinction between working memory and long-term memory as separate systems, so we use these terms pragmatically as referring to memory phenomena over short time spans (on the order of seconds) and longer time spans; so far, SOB-CS has addressed only the former. The role of long-term memory is particularly pertinent to modeling the complex-span task. The complex-span paradigm is strikingly similar to the continuous-distractor paradigm (Bjork & Whitten, 1974) that has been commonly interpreted as reflecting recall entirely from long-term memory. Meanwhile, a substantial body of evidence from experimental (D. McCabe, 2008) and correlational (Unsworth, 2010; Unsworth, Brewer, & Spillers, 2009) studies, as well as from neuroscience (Chein et al., 2011), confirms that processes and performance on complex-span tasks are related to long-term memory (Unsworth & Engle, 2007).
The relation of working memory to long-term memory most likely goes in both directions: On the one hand, knowledge in long-term memory contributes to recall in working memory tasks. This is already acknowledged by all models that assume redintegration of distorted memory traces (e.g., Nairne, 1990; Schweickert, 1993), because redintegration requires intact long-term memory representations of recall candidates. Our simulation of individual differences in span tasks assumes that these individual differences arise in part from variation in the c parameter, which can be interpreted as reflecting the discriminability of representations in long-term memory. On the other hand, processes on working memory tasks generate memory traces that long outlast the individual trial (D. McCabe, 2008), exerting effects across trials that are sometimes beneficial, as in the so-called Hebb effect (Hebb, 1961), and sometimes harmful, as in proactive interference (Bunting, 2006).
So far, SOB-CS models only individual trials. After every trial, the weight matrix is reset to a state that reflects previous learning events in a very generic fashion (i.e., simply adding random noise to all weights with standard deviation N o ). Therefore, SOB-CS cannot yet account for interference or facilitation across trials. An obvious first step to account for effects beyond single trials would be to assume that the weight matrix is not reset after each trial, but instead squashed (i.e., multiplied by a value between 0 and 1). Squashing would be a mechanism for removing no-longer-relevant information in a wholesale manner, which is different from the targeted removal of individual representations. Incomplete squashing would leave traces of previous trials, giving rise to proactive interference. We anticipate that more sophisticated mechanisms will be needed to account for other aspects of the link between long-term and working memory.
One set of mechanisms has been proposed by one of us to explain the relationship between working memory and episodic memory (Farrell, 2012). Like SOB-CS, this model assumes that items are associated with a representation of temporal context, but that some portion of the context is used to bind together temporally adjacent items into episodic clusters. Successive lists in a working memory experiment would be partially separated by temporal context, which contributes to reducing interference between them. In simulating the effects of distractor activity in free recall (analogous to the complex-span tasks simulated here), Farrell assumed that distractors are clustered together with the item that they immediately follow, such that they are associated with the same cluster-level context as the preceding item. This parallels the assumptions made in SOB-CS and opens some avenues of integration across the two models. Other neural-network models of serial recall are making progress in explaining the effects of long-term learning on immediate recall (Botvinick & Plaut, 2006; Burgess & Hitch, 2006; Page & Norris, 2009), and we see this as an encouraging development from which we hope to learn for a future extension of our model.
Relation to other theories of working memory
In this section, we compare SOB-CS to other theories of short-term and working memory, beginning with a brief review of other computational models, followed by an attempt to relate our model to some of the most influential verbal theories of working memory.
Computational models
As already noted, SOB-CS is closely related to other formal models of serial recall because it originated in that tradition. As a consequence, SOB-CS retains the achievements of previous versions of SOB in accounting for a multitude of phenomena in simple span (Lewandowsky & Farrell, 2008b), thus constituting the first computational model of working memory that generalizes across two paradigms, serial recall and complex span.
Several other computational models have addressed working memory, but they are concerned with paradigms that are beyond the current scope of SOB-CS (Ashby, Ell, Valentin, & Casale, 2005; O’Reilly & Frank, 2005; Oberauer & Kliegl, 2006). We are aware of only two other models that address complex span, and that are therefore direct competitors with SOB-CS: the ACT-R-based model of Daily et al. (2001) and our computational implementation of TBRS (Oberauer & Lewandowsky, 2011).
Daily et al. (2001) explained capacity limits in working memory through two factors, one being decay and the other a limited resource for activating representations that limits the degree to which, during rehearsal and retrieval, the correct item can be activated more strongly than competing items. The model accounts reasonably well for some of the benchmark phenomena known at the time: the decline of accuracy with memory-list length and the serial-position curve. The model also gives an account of individual differences in serial-position curves for different list lengths by varying a single parameter—namely, the amount of available resources. Daily et al. published their model before the benchmark findings related to cognitive load emerged, but their model has the potential to account for these effects in a way similar to the TBRS* model, because the model includes decay and rehearsal, and it includes a processing bottleneck so that the model can rehearse only when it is not engaged in processing a distractor.
We regard TBRS*, our computational implementation of TBRS, as the strongest competitor to SOB-CS for explaining experimental results with complex-span tasks, and we therefore focused initially on addressing evidence that has been cited as being uniquely supportive of TBRS (viz., the cognitive-load function). We have shown that SOB-CS successfully handles those data—and in two regards does so even more successfully than TBRS*. First, SOB-CS gives a better account of the cognitive-load effect when it is broken down into the effects of operation duration and free time (Fig. 7). Second, SOB-CS correctly predicts the joint effects of number of distractor operations, similarity between successive distractors, and serial position, whereas TBRS* could not reproduce the pattern of results even with favorable ad-hoc assumptions (see Fig. 8).
We acknowledge that the comparison between SOB-CS and TBRS* can be regarded as unfair, because TBRS* was implemented by ourselves rather than by the authors of the TBRS theory. Thus, despite our best efforts to make TBRS* as strong as possible, it is conceivable that a better way exists of implementing the TBRS theory as a computational model. The mere possibility that this is the case does not render irrelevant the challenges arising for the TBRS theory from the present results. If the TBRS theory is to explain the benchmark data of complex span, then there must be at least one computational implementation of the theory that can coherently explain them. In other words, among the many different ways in which all of the details left out by the verbal theory can be filled in, there should be at least one that works. It is now incumbent on proponents of the theory to show that there is an implementation that fixes the problems noted above and at the same time retains the success of TBRS* in accounting for a broad range of other findings (Oberauer & Lewandowsky, 2011).
Verbal theories of working memory
Many readers will ask: Where do I find in SOB-CS the familiar concepts of contemporary theories of working memory? The best-known theories of working memory today are only verbally formulated. They are often broader in scope than computational models, but lack the precision of computational models. Here we relate SOB-CS to some of the better-known verbal theories of working memory.
The working memory theory of Baddeley (1986, 2000)
Probably the most popular theory of working memory is the one introduced by Baddeley and Hitch (1974) and developed further by Baddeley (1986, 2000). It consists of four interacting components: a central executive, an episodic buffer, and two slave systems for domain-specific maintenance, namely the phonological loop (for verbal information) and the visuospatial sketch pad (for visual object information and spatial location). The episodic buffer serves as a device for maintaining integrated representations that cut across domain boundaries. At first glance, it might be tempting to relate the memory mechanism of SOB-CS—that is, the two-layer architecture, the principles of Hebbian association, and the redintegration mechanism—to the two slave systems in Baddeley’s model. However, in SOB-CS the distinction of two domain-specific subsystems is unnecessary, because the double dissociations of verbal and visuospatial contents emerges from the model through the lack of superposition interference between disjoint representational domains. For the same reason, SOB-CS does not need a separate memory system for entities integrating verbal and nonverbal features, such as the episodic buffer; verbal and nonverbal features can be bound together simply by associating them with the same context representation. SOB-CS decidedly differs from Baddeley’s model in that it assumes no time-based decay of phonological (or other) memory traces. We regard this as a strength of our model, because there is no convincing evidence for decay in verbal short-term and working memory (Lewandowsky, Oberauer, & Brown, 2009).
Nothing in SOB-CS corresponds to the central executive in Baddeley’s (1986, 2000) model. Clearly, a complete model of working memory will have to spell out explicitly the executive processes that control its contents. We have only begun to do so by formalizing the basic processes of encoding and removal of representations from memory. Eventually, models of the memory component of working memory such as SOB-CS will have to be combined with computational models of the executive processes working on the memory contents (e.g., Botvinick, Braver, Barch, Carter, & Cohen, 2001; Chatham et al., 2011; Verguts & Notebaert, 2008).
The embedded-process theory of Cowan (1995, 2005)
Cowan (1995, 2005) conceptualized working memory as consisting of two embedded components, the activated part of long-term memory and the focus of attention. Activated long-term memory has no capacity limit, but its contents are prone to forgetting due to decay and interference. The focus has a limited capacity of approximately four chunks that it protects from decay and interference.
It is not obvious how to map SOB-CS onto the main constructs in Cowan’s theory. The focus of attention in SOB-CS is limited to a single content–context conjunction at any time, akin to the notion of a one-chunk focus of attention in other, related theories (McElree, 2006; Oberauer, 2002), not to a focus encompassing up to four chunks. The two-layer architecture and its connecting-weight matrix, which serves to maintain memory of several items, does not fit the notion of Cowan’s focus, either: In contrast to Cowan’s focus, the weight-based memory of SOB-CS is not limited to a discrete number of chunks, it is not immune to interference, and it bears no conceptual relation to attention. If anything, the weight matrix of SOB-CS could be considered as fleshing out the contribution of ancillary mechanisms serving maintenance functions over and above the focus of attention in Cowan’s theory. Thus, there is currently no counterpart for Cowan’s focus of attention in SOB-CS. This might be a weakness of our model, insofar as there is evidence for the characteristic features of Cowan’s focus—a fixed capacity limit of four chunks and immunity to interference for those chunks—that cannot be explained within SOB-CS. The main evidence for a focus with these characteristics comes from recognition paradigms that are, so far, outside the scope of SOB-CS (Cowan, Johnson, & Saults, 2005; Rouder et al., 2008; Saults & Cowan, 2007); this observation underscores the need to extend our model to these paradigms.
One of us (Oberauer, 2002, 2009) has proposed a framework similar to Cowan’s in which the region of direct access roughly corresponds to Cowan’s focus of attention. In contrast to Cowan’s focus, the region of direct access is not assumed to have a fixed capacity limit in terms of a “magical number” of chunks, and it is not assumed to be immune to interference. Rather, the capacity limit of the direct-access region is attributed to interference between different item–context bindings that are maintained simultaneously. In keeping with this idea, interference between item–context associations plays the main role in explaining the limitations on retrieval in SOB-CS. Thus, the associative memory mechanism of SOB-CS can be tentatively interpreted as a model of the direct-access region, and the current contents of the item and position layers can be regarded as the contents of the one-chunk focus of attention in the theory of Oberauer (2002, 2009).
The theory of executive attention of Engle and Kane
Engle, Kane, and their colleagues developed a theory of working memory addressing primarily individual differences (Engle et al., 1999; Kane et al., 2007; Kane & Engle, 2002). They described performance on the complex-span task as reflecting contributions from domain-specific storage systems, plus a general resource for controlled, or executive, attention. They define executive attention as the ability to maintain goal-relevant representations in the face of distraction. In the context of SOB-CS, removal of no-longer-relevant representations from memory is the mechanism for minimizing interference from potentially distracting representations. Therefore, individual differences in the removal parameter could provide an explanation for the associations between complex-span and executive-attention measures without any memory component, such as the Stroop effect (Kane & Engle, 2003) and the antisaccade task (Unsworth et al., 2004). At this point of model development, distractor removal is the only control mechanism explicitly modelled, but other control mechanisms, such as the degree to which irrelevant information can be prevented from entering working memory, are also likely to contribute to individual differences in working memory performance (Awh & Vogel, 2008; Hasher et al., 1999; Jost et al., 2010). We envision that a parameter for the degree of filtering at encoding will be added in a later extension of the model.
The executive-attention view could be interpreted in the context of SOB-CS as the claim that shared variance between complex span and measures of fluid intelligence comes primarily from variance in the efficiency of the executive-control parameters. An alternative view has been advanced by Colom, Rebollo, Abad, and Shih (2006), who argued that variance in the “storage” component of complex (as well as simple) span is responsible for the strong correlation with fluid intelligence. In the context of SOB-CS, this view would imply that fluid intelligence is mostly related to the memory parameters (e.g., the distinctiveness parameter c). A future analysis of individual differences in complex span in terms of the parameters of SOB-CS might be instrumental in moving beyond the dichotomy of “storage” versus “executive attention” and provide insights into which mechanisms and processes are responsible for the differences between individuals with high and with low complex span.
Neuroscientific theories of working memory
Theories about the neuronal substrate of working memory can be divided into two classes. The majority of theories assume that retention in working memory relies on persistent neural firing. An alternative view is that the contents of working memory are maintained by rapid changes of synaptic weights (e.g., Mongillo, Barak, & Tsodyks, 2008). In SOB-CS, memory is entirely based on the connection weights, and as such our model is most compatible with synaptic-change-based theories of working memory. Whereas there is compelling evidence for load-dependent neural activity during working memory retention (Curtis & D’Esposito, 2003; Vogel et al., 2005), recent evidence has suggested that this neural activity might not directly code the contents of working memory. Rather than remaining active during the entire retention interval, the patterns of neural activity correlated with working memory contents are reactivated when needed for processing (Barak, Tsodyks, & Romo, 2010; Lewis-Peacock et al., 2011). These findings support weight-based models such as SOB-CS, which (approximately) reproduce item representations as activation patterns from the weight matrix when given a cue related to that item.
At the same time, mapping mechanisms in SOB-CS to neuronal processes is far from straightforward. For instance, there is no obvious counterpart in SOB-CS for load-dependent neural activity during the retention interval. One possibility arises from the model of short-term synaptic potentiation of Mongillo et al. (2008), according to which rapid weight changes require recurrent nonspecific neural activity to be upheld over time. As more items are encoded, the weights in the weight matrix deviate further from zero, and as a consequence, more neural activity might be needed to uphold the weight matrix. Obviously, this is a very speculative attempt to reconcile our model with neuroscientific evidence. An important step toward tightening the link between weight-based models of working memory and neuronal mechanisms would be to investigate the neural substrates of rapid synaptic weight changes.
Conclusions
SOB-CS provides new answers to a number of pressing questions in working memory research.
First, with SOB-CS we offer a computational model of complex span that explains forgetting entirely through interference. Thus, we provide a simple answer to one of the key questions of working memory research: Why is working memory capacity limited? In SOB-CS, the capacity limit arises entirely from interference. This explanation is more parsimonious than any alternative, because all theories of working memory acknowledge the existence of interference, and those that explain the capacity limit by other processes, such as decay or limited resources, must assume these processes in addition to interference. We have shown that a purely interference-based model can explain benchmark data, such as the cognitive-load effect, that constitute the empirical foundation for the currently most viable decay-based theory (Barrouillet et al., 2007; Barrouillet et al., 2011).
Our computational model provides a clear, unambiguous formulation of the mechanisms of interference in working memory, which serves as a starting point for a detailed empirical investigation of these processes. We distinguish two kinds of interference, one arising from superposition, the other arising from confusion. We show that different kinds of similarity modulate these two kinds of interference in different ways. The model generates new and in part counterintuitive predictions about the effect of item–distractor similarity, which were experimentally confirmed (Oberauer et al., 2012).
A second question that has long been debated in the working memory literature concerns the relation between memory and processing. SOB-CS accounts for the full range of benchmark findings relating to this issue. The key pair of assumptions that we make is that all information attended to during a concurrent processing task is encoded into memory, and thereby potentially interferes with other memories, and that interference can be reduced by gradual removal of irrelevant information. These assumptions lead to the correct predictions that the cognitive-load effect is primarily an effect of the free time between distractor operations (Simulation 2) and that the number of distractors has an effect on memory if and only if the distractors differ from each other (Simulation 3).
A new theoretical discovery emerging from our modeling efforts is the strong link between interference and removal. Any model that explains the limited capacity of working memory without appealing to decay must assume some form of removal of no-longer-relevant information. Without removal, the available capacity would soon be cluttered with irrelevant information. SOB-CS is the first model with an explicit, well-defined mechanism of removal.
Our modeling results also pose a challenge to theories assuming that memory representations are actively maintained by rehearsal or refreshing. As discussed above, we do not deny a potential role for these processes. However, our modeling results have shown that benchmark findings that so far have been interpreted as strong evidence for rehearsal or refreshing (in particular, the cognitive-load effect) can be explained without those processes. This finding raises the question of which phenomena demand the assumption of rehearsal or refreshing. Other modeling work (Oberauer & Lewandowsky, 2008, 2011) has shown that, even in the context of decay-based models, rehearsal is effective only in a narrow set of circumstances. Taken together, these demonstrations imply that rehearsal and refreshing are not the only conceivable processes of active restoration; removal of irrelevant information should be taken seriously as a contender. We have developed an explicit computational model of how removal could work; we hope that this encourages proponents of rehearsal or refreshing to specify with equal precision what happens when people rehearse or refresh.
Another longstanding question is whether working memory is a unitary system or should be conceptualized as consisting of several domain-specific subsystems. Proponents of both views can point to considerable evidence in their favor. Within our distributed connectionist modeling framework, we offer a principled explanation that accommodates the evidence cited in favor of both sides of the debate. Working memory is a unitary system that operates with representations from different content domains. Different content domains are characterized by different feature dimensions, which are represented by different sets of units in the content layer. To the degree that the contents of tasks carried out concurrently use representations from different domains, these tasks do not interfere, because the representations do not overlap in the neural network. In practice, however, hardly any task is content-pure, and therefore even nominally “visuospatial” tasks involve some verbal features, and nominally “verbal” tasks involve some visuospatial features. This explains why tasks used to represent different content domains nevertheless interfere with each other to some degree.
Evidence for both domain-general and domain-specific aspects of working memory also comes from correlational studies. Various measures of working memory capacity share a large proportion of their variance, thus pointing to a nonnegligible source of variance reflecting general working memory capacity. At the same time, verbal and visuospatial span tasks load on separate, though correlated, factors. We have shown that the patterns of correlations between various simple- and complex-span tasks can be explained with SOB-CS by assuming individual differences in two parameters, one domain-specific parameter that governs the distinctiveness of memory representations in simple- and complex-span tasks, and one general parameter affecting the removal of irrelevant information, which is particularly important in tasks combining memory with processing demands. Again, a unitary system operating on domain-specific representations explains the full range of results.
In conclusion, we have proposed the first purely interference-based computational model for a key paradigm in research on working memory. The model explicitly describes the basic mechanisms of working memory: encoding of items in their relative positions, retrieval of individual items by positional cueing, interference from concurrent processing, and the control of interference by removal of no-longer-relevant information. The model successfully accounts for a number of benchmark findings from complex-span tasks and makes successful new predictions. We hope that our work will encourage other researchers to make competing theoretical ideas equally explicit, so that the debate about the mechanisms of working memory can be advanced to a greater level of precision.
Notes
The program code is also available at our web pages: www.cogsciwa.com; www.psychologie.uzh.ch/fachrichtungen/allgpsy/Team/Oberauer_en.html; http://seis.bris.ac.uk/~pssaf/publications.html.
The similarity between neighboring positions was labeled t c in previous publications; here we rename it to s p to avoid confusion with the time parameters.
The actual similarity between items and distractors is lower (e.g., about 0.1 in the case of letters and digits) because items are derived from the item prototype and distractors are derived from the distractor prototype.
Jolicœur and Dell’Acqua (1998) fitted a model to the data of three of their experiments. In that model one parameter, τ 1 i, is the mean of an exponentially distributed time variable that represents the sum of the times for sensory and perceptual processing and for short-term consolidation of a single item. These means were estimated to be 0.304, 0.150, and 0.275 s for the three modeled experiments (4, 6, and 7), respectively. The rate of the exponential function is the inverse of the mean: that is, 3.3, 6.7, and 3.6, respectively, for the three experiments. The rate is higher for Experiment 6 than for the other experiments, and Jolicœur and Dell’Acqua argued that this could be because in Experiment 6, a single letter was to be encoded into memory on every trial, whereas the other experiments involved a mixture of trials with one and with three letters. In this regard, Experiment 6 might be the most representative one for the encoding of single letters in a serial-recall task.
For instance, span at a cognitive-load level .33 is worse than expected from a strictly linear function, and span at the following load level (.37) is better than expected. Between the first and the second of these data points, operation duration is more than doubled (from 0.3 to 0.7), and free time is doubled (from 0.6 to 1.2). The increase of operation duration, however, has only a negligible effect, whereas the increase of free time has a more substantial effect. Therefore, span at the higher load level exceeds that at the lower load level in this particular comparison, and in the others that generate nonmonotonicities in Fig. 5.
We investigated other refreshing schedules in the context of TBRS* (Oberauer & Lewandowsky, 2011), such as selecting items for refreshing at random or refreshing only the last-presented item. These resulted in a serial-position curve with strong recency and little if any primacy, because early list items have the longest retention intervals, and therefore suffer most from decay. We believe that we investigated all simple and straightforward refreshing schedules, although other, more elaborate schedules might be compatible with the largely additive effects of serial positions and distractors, and at the same time still generate the correct shape of the serial-position curve. As the space of possible refreshing schedules is vast, it is impossible to explore them all. The onus is now on decay theorists to propose a schedule that brings their theory in line with the data.
Unsworth and Engle (2006), reanalyzing data from Kane et al. (2004), reported serial-position effects on correct recall, intrusions, and omissions that differed in some regards from published data with simple span tasks and from our data from complex-span tasks. Unsworth and Engle (2006) found that the probability of omissions was largest at the first and last output positions and that the probability of intrusions was largest at the second output position, and from that point decreased monotonically with output position. We believe that this unusual pattern was a consequence of the lack of control over output order: Participants were asked to write the memoranda into slots on an answer sheet; they could fill the slots in any order. It is likely that participants often began recall by putting the last list item in the last slot (Lewandowsky, Brown, & Thomas, 2009), thereby avoiding intrusion errors at that position. Because of the apparently uncontrolled output order in the study of Unsworth and Engle (2006), we do not compare our simulations to their detailed analysis of errors. This critique does not invalidate the analyses of Kane et al. (2004), which relied on scores aggregated across serial positions.
There are reasons to believe that this problem is not specific to SOB-CS. Existing computational models of working memory, including those that assume a central role for rehearsal, do not model it in detail (Page & Norris, 1998). In a previous modeling study, we found that even in the context of a decay-based model, rehearsal can be detrimental rather than beneficial (Oberauer & Lewandowsky, 2008).
References
Aldridge, J. W., Garcia, H. R., & Mena, G. (1987). Habituation as a necessary condition for maintenance rehearsal. Journal of Memory and Language, 26, 632–637.
Alloway, T. P., Gathercole, S., & Pickering, S. J. (2006). Verbal and visuospatial short-term and working memory in children: Are they separable? Child Development, 77, 1698–1716.
Anderson, J. A. (1991). Why, having so many neurons, do we have so few thoughts? In W. E. Hockley & S. Lewandowsky (Eds.), Relating theory and data: Essays on human memory in honor of Bennet B. Murdock (pp. 477–507). Hillsdale: Erlbaum.
Anderson, J. A. (1995). An introduction to neural networks. Cambridge, MA: MIT Press.
Anderson, J. A., Silverstein, J. W., Ritz, S. A., & Jones, R. S. (1977). Distinctive features, categorical perception, and probability learning: Some applications of a neural model. Psychological Review, 84, 413–451. doi:10.1037/0033-295X.84.5.413
Ashby, F. G., Ell, S. W., Valentin, V. V., & Casale, M. B. (2005). FROST: A distributed neurocomputational model of working memory maintenance. Journal of Cognitive Neuroscience, 17, 1728–1743.
Awh, E., & Vogel, E. K. (2008). The bouncer in the brain. Nature Neuroscience, 11, 5–6.
Baddeley, A. (1986). Working memory. Oxford, U.K.: Oxford University Press, Clarendon Press.
Baddeley, A. D. (2000). The episodic buffer: A new component of working memory? Trends in Cognitive Sciences, 4, 417–423. doi:10.1016/S1364-6613(00)01538-2
Baddeley, A. D., & Hitch, G. J. (1974). Working memory. In G. H. Bower (Ed.), The psychology of learning and motivation: Advances in research and theory (Vol. 8, pp. 47–89). New York, NY: Academic Press.
Bailey, H., Dunlosky, J., & Kane, M. J. (2008). Why does working memory span predict complex cognition? Testing the strategy affordance hypothesis. Memory & Cognition, 36, 1383–1390.
Bar-Anan, Y., Liberman, N., Trope, Y., & Algom, D. (2007). Automatic processing of psychological distance: Evidence from a Stroop task. Journal of Experimental Psychology: General, 136, 610–622.
Barak, O., Tsodyks, M., & Romo, R. (2010). Neuronal population coding of parametric working memory. Journal of Neuroscience, 30, 9424–9430.
Barrouillet, P., Bernardin, S., & Camos, V. (2004). Time constraints and resource sharing in adults’ working memory spans. Journal of Experimental Psychology: General, 133, 83–100. doi:10.1037/0096-3445.133.1.83
Barrouillet, P., Bernardin, S., Portrat, S., Vergauwe, E., & Camos, V. (2007). Time and cognitive load in working memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 33, 570–585. doi:10.1037/0278-7393.33.3.570
Barrouillet, P., Gavens, N., Vergauwe, E., Gaillard, V., & Camos, V. (2009). Working memory span development: A time-based resource-sharing model account. Developmental Psychology, 45, 477–490. doi:10.1037/a0014615
Barrouillet, P., Portrat, S., & Camos, V. (2011). On the law relating processing to storage in working memory. Psychological Review, 118, 175–192. doi:10.1037/a0022324
Bayliss, D. M., Jarrold, C., Baddeley, A. D., Gunn, D. M., & Leigh, E. (2005). Mapping the developmental constraints on working memory span performance. Developmental Psychology, 41, 579–597. doi:10.1037/0012-1649.41.4.579
Bayliss, D. M., Jarrold, C., Gunn, D. M., & Baddeley, A. D. (2003). The complexities of complex span: Explaining individual differences in working memory in children and adults. Journal of Experimental Psychology: General, 132, 71–92. doi:10.1037/0096-3445.132.1.71
Bhatarah, P., Ward, G., & Tan, L. (2008). Examining the relationship between free recall and immediate serial recall: The serial nature of recall and the effect of test expectancy. Memory & Cognition, 36, 20–34. doi:10.3758/MC.36.1.20
Bjork, R. A., & Whitten, W. B. (1974). Recency-sensitive retrieval processes in long-term free recall. Cognitive Psychology, 6, 173–189. doi:10.1016/0010-0285(74)90009-7
Botvinick, M. M., Braver, T. S., Barch, D. M., Carter, C. S., & Cohen, J. D. (2001). Conflict monitoring and cognitive control. Psychological Review, 108, 624–652. doi:10.1037/0033-295X.108.3.624
Botvinick, M. M., & Plaut, D. C. (2006). Short-term memory for serial order: A recurrent neural network model. Psychological Review, 113, 201–233.
Brown, G. D. A., Neath, I., & Chater, N. (2007). A temporal ratio model of memory. Psychological Review, 114, 539–576. doi:10.1037/0033-295X.114.3.539
Brown, G. D. A., Preece, T., & Hulme, C. (2000). Oscillator-based memory for serial order. Psychological Review, 107, 127–181. doi:10.1037/0033-295X.107.1.127
Brown, J. (1958). Some tests of the decay theory of immediate memory. Quarterly Journal of Experimental Psychology, 10, 12–21.
Brown, S. D., & Heathcote, A. (2008). The simplest complete model of choice response time: Linear ballistic accumulation. Cognitive Psychology, 57, 153–178. doi:10.1016/j.cogpsych.2007.12.002
Bunting, M. F. (2006). Proactive interference and item similarity in working memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 32, 183–196.
Burgess, N., & Hitch, G. J. (1999). Memory for serial order: A network model of the phonological loop and its timing. Psychological Review, 106, 551–581. doi:10.1037/0033-295X.106.3.551
Burgess, N., & Hitch, G. J. (2006). A revised model of short-term memory and long-term learning of verbal sequences. Journal of Memory and Language, 55, 627–652.
Carretti, B., Cornoldi, C., De Beni, R., & Palladino, P. (2004). What happens to information to be suppressed in working memory tasks? Short and long term effects. Quarterly Journal of Experimental Psychology, 57A, 1059–1084.
Case, R., Kurland, M., & Goldberg, J. (1982). Operational efficiency and the growth of short-term memory span. Journal of Experimental Child Psychology, 33, 386–404.
Chatham, C. H., Herd, S. A., Brant, A. M., Hazy, T. E., Miyake, A., O’Reilly, R., & Friedman, N. P. (2011). From an executive network to executive control: A computational model of the n-back task. Journal of Cognitive Neuroscience, 23, 3598–3619. doi:10.1162/jocn_a_00047
Chein, J. M., Moore, A. B., & Conway, A. R. A. (2011). Domain-general mechanisms of complex working memory span. NeuroImage, 54, 550–559.
Colom, R., Rebollo, I., Abad, F. J., & Shih, P. C. (2006). Complex span tasks, simple span tasks, and cognitive abilities: A reanalysis of key studies. Memory & Cognition, 34, 158–171.
Conlin, J. A., Gathercole, S. E., & Adams, J. W. (2005). Stimulus similarity decrements in children’s working memory span. Quarterly Journal of Experimental Psychology, 58A, 1434–1446.
Conway, A. R. A., Cowan, N., Bunting, M. F., Therriault, D. J., & Minkoff, S. R. B. (2002). A latent variable analysis of working memory capacity, short-term memory capacity, processing speed, and general fluid intelligence. Intelligence, 30, 163–183.
Conway, A. R. A., Jarrold, C., Kane, M. J., Miyake, A., & Towse, J. N. (Eds.). (2007). Variation in working memory. New York, NY: Oxford University Press.
Conway, A. R. A., Kane, M. J., Bunting, M. F., Hambrick, D. Z., Wilhelm, O., & Engle, R. W. (2005). Working memory span tasks: A methodological review and user’s guide. Psychonomic Bulletin & Review, 12, 769–786. doi:10.3758/BF03196772
Conway, A. R. A., Kane, M. J., & Engle, R. W. (2003). Working memory capacity and its relation to general intelligence. Trends in Cognitive Sciences, 7, 547–552. doi:10.1016/j.tics.2003.10.005
Corman, C. D., & Wickens, D. D. (1968). Retroactive inhibition in short-term memory. Journal of Verbal Learning and Verbal Behavior, 7, 16–19.
Cowan, N. (1995). Attention and memory: An integrated framework. New York, NY: Oxford University Press.
Cowan, N. (2005). Working memory capacity. New York, NY: Psychology Press.
Cowan, N., Johnson, T. D., & Saults, J. S. (2005). Capacity limits in list item recognition: Evidence from proactive interference. Memory, 13, 293–299.
Cowan, N., Saults, J. S., Elliott, E. M., & Moreno, M. V. (2002). Deconfounding serial recall. Journal of Memory and Language, 46, 153–177.
Craik, F. I. M., & Lockhart, R. S. (1972). Levels of processing: A framework for memory research. Journal of Verbal Learning and Verbal Behavior, 11, 671–684. doi:10.1016/S0022-5371(72)80001-X
Curtis, C. E., & D’Esposito, M. (2003). Persistent activity in the prefrontal cortex during working memory. Trends in Cognitive Sciences, 7, 415–423. doi:10.1016/S1364-6613(03)00197-9
Daily, L. Z., Lovett, M. C., & Reder, L. M. (2001). Modeling individual differences in working memory performance: A source activation account. Cognitive Science, 25, 315–353.
Dale, H. C. A., & Gregory, M. (1966). Evidence of semantic coding in short-term memory. Psychonomic Science, 5, 153–154.
Daneman, M., & Carpenter, P. A. (1980). Individual differences in working memory and reading. Journal of Verbal Learning and Verbal Behavior, 19, 450–466.
Daneman, M., & Merikle, P. M. (1996). Working memory and language comprehension: A meta-analysis. Psychonomic Bulletin & Review, 3, 422–433. doi:10.3758/BF03214546
De Beni, R., Palladino, P., Pazzaglia, P., & Cornoldi, C. (1998). Increases in intrusion errors and working memory deficit of poor comprehenders. Quarterly Journal of Experimental Psychology, 51A, 305–320.
Duncan, M., & Lewandowsky, S. (2005). The time course of response suppression: No evidence for a gradual release from inhibition. Memory, 13, 236–246.
Dunlosky, J., & Kane, M. J. (2007). The contributions of strategy use to working memory span: A comparison of strategy assessment methods. Quarterly Journal of Experimental Psychology, 60, 1227–1245.
Ecker, U. K. H., Lewandowsky, S., Oberauer, K., & Chee, A. E. H. (2010). The components of working memory updating: An experimental decomposition and individual differences. Journal of Experimental Psychology: Learning, Memory, and Cognition, 36, 170–189.
Emerson, M. J., & Miyake, A. (2003). The role of inner speech in task switching: A dual-task investigation. Journal of Memory and Language, 48, 148–168.
Engle, R. W., Cantor, J., & Carullo, J. J. (1992). Individual differences in working memory and comprehension: A test of four hypotheses. Journal of Experimental Psychology: Learning, Memory, and Cognition, 18, 972–992.
Engle, R. W., Tuholski, S. W., Laughlin, J. E., & Conway, A. R. A. (1999). Working memory, short-term memory, and general fluid intelligence: A latent-variable approach. Journal of Experimental Psychology: General, 128, 309–331. doi:10.1037/0096-3445.128.3.309
Farrell, S. (2006). Mixed-list phonological similarity effects in delayed serial recall. Journal of Memory and Language, 55, 587–600.
Farrell, S. (2012). Temporal clustering and sequencing in short-term memory and episodic memory. Psychological Review, 119, 223–271. doi:10.1037/a0027371
Farrell, S., & Lewandowsky, S. (2002). An endogenous distributed model of ordering in serial recall. Psychonomic Bulletin & Review, 9, 59–79. doi:10.3758/BF03196257
Farrell, S., & Lewandowsky, S. (2003). Dissimilar items benefit from phonological similarity in serial recall. Journal of Experimental Psychology: Learning, Memory, and Cognition, 29, 838–849. doi:10.1037/0278-7393.29.5.838
Farrell, S., & Lewandowsky, S. (2004). Modelling transposition latencies: Constraints for theories of serial order memory. Journal of Memory and Language, 51, 115–135. doi:10.1016/j.jml.2004.03.007
Farrell, S., & Lewandowsky, S. (2010). Computational models as aids to better reasoning in psychology. Current Directions in Psychological Science, 19, 329–335.
Fawcett, J. M., & Taylor, T. L. (2008). Forgetting is effortful: Evidence from reaction time probes in an item-method directed forgetting task. Memory & Cognition, 36, 1168–1181.
Fitzgerald, P., & Broadbent, D. E. (1985). Order of report and the structure of temporary memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 11, 217–228.
Garavan, H. (1998). Serial attention within working memory. Memory & Cognition, 26, 263–276.
Gathercole, S. E., Pickering, S. J., Ambridge, B., & Wearing, H. (2004). The structure of working memory from 4 to 15 years of age. Developmental Psychology, 40, 177–190. doi:10.1037/0012-1649.40.2.177
Haberlandt, K., Thomas, J. G., Lawrence, H., & Krohn, T. (2005). Transposition asymmetry in immediate serial recall. Memory, 13, 274–282.
Hale, S., Myerson, J., Rhee, S. H., Weiss, G. S., & Abrams, R. A. (1996). Selective interference with the maintenance of location information in working memory. Neuropsychology, 10, 228–240.
Hasher, L., & Zacks, R. T. (1988). Working memory, comprehension, and aging: A review and a new view. In G. H. Bower (Ed.), The psychology of learning and motivation: Advances in research and theory (Vol. 2, pp. 193–225). San Diego: Academic Press. doi:10.1016/S0079-7421(08)60041-9
Hasher, L., Zacks, R. T., & May, C. P. (1999). Inhibitory control, circadian arousal, and age. In D. Gopher & A. Koriat (Eds.), Attention and performance XVII: Cognitive regulation of performance. Interaction of research and theory (pp. 653–675). Cambridge: MIT Press.
Hebb, D. O. (1961). Distinctive features of learning in the higher animal. In J. F. Delafresnaye (Ed.), Brain mechanisms and learning (pp. 37–46). Oxford, U.K.: Blackwell.
Henson, R. N. A. (1996). Short-term memory for serial order. Dissertation, University of Cambridge. Retrieved from www.mrc-cbu.cam.ac.uk/~rh01/thesis.html
Henson, R. N. A. (1998a). Item repetition in short-term memory: Ranschburg repeated. Journal of Experimental Psychology: Learning, Memory, and Cognition, 24, 1162–1181. doi:10.1037/0278-7393.24.5.1162
Henson, R. N. A. (1998b). Short-term memory for serial order: The start–end model. Cognitive Psychology, 36, 73–137.
Henson, R. N. A., Norris, D. G., Page, M. P. A., & Baddeley, A. D. (1996). Unchained memory: Error patterns rule out chaining models of immediate serial recall. Quarterly Journal of Experimental Psychology, 49A, 80–115.
Hudjetz, A., & Oberauer, K. (2007). The effects of processing time and processing rate on forgetting in working memory: Testing four models of the complex span paradigm. Memory & Cognition, 35, 1675–1684.
Hull, A. J. (1973). A letter-digit matrix of auditory confusions. British Journal of Psychology, 64, 579–585.
Hyde, T. S., & Jenkins, J. J. (1969). Differential effects of incidental tasks on the organization of recall of a list of highly associated words. Journal of Experimental Psychology, 82, 472–481.
Jacobs, J. (1887). Experiments on “prehension. Mind, 12, 75–59.
Jahnke, J. C. (1969). Output interference and the Ranschburg effect. Journal of Verbal Learning and Verbal Behavior, 8, 614–621.
Jarrold, C., Tam, H., Baddeley, A. D., & Harvey, C. E. (2010). The nature and the position of processing determines why forgetting occurs in working memory tasks. Psychonomic Bulletin & Review, 17, 772–777. doi:10.3758/PBR.17.6.772
Jarrold, C., Tam, H., Baddeley, A. D., & Harvey, C. E. (2011). How does processing affect storage in working memory tasks? Evidence for both domain-general and domain-specific effects. Journal of Experimental Psychology: Learning, Memory, and Cognition, 37, 688–705.
Jolicœur, P., & Dell’Acqua, R. (1998). The demonstration of short-term consolidation. Cognitive Psychology, 36, 138–202. doi:10.1006/cogp. 1998.0684
Jonides, J., Lewis, R. L., Nee, D. E., Lustig, C. A., Berman, M. G., & Moore, K. S. (2008). The mind and brain of short-term memory. Annual Review of Psychology, 59, 193–224. doi:10.1146/annurev.psych.59.103006.093615
Jost, K., Bryck, R. L., Vogel, E. K., & Mayr, U. (2010). Are old adults just like low working memory young adults? Filtering efficiency and age differences in visual working memory. Cerebral Cortex, 21, 147–1154.
Kaakinen, J. K., & Hyönä, J. (2007). Strategy use in the reading span test: An analysis of eye movements and reported encoding strategies. Memory, 15, 634–646.
Kane, M. J., Bleckley, M. K., Conway, A. R. A., & Engle, R. W. (2001). A controlled-attention view of working-memory capacity. Journal of Experimental Psychology: General, 130, 169–183. doi:10.1037/0096-3445.130.2.169
Kane, M. J., Conway, A. R. A., Hambrick, D. Z., & Engle, R. W. (2007). Variation in working memory capacity as variation in executive attention and control. In A. R. A. Conway, C. Jarrold, M. J. Kane, A. Miyake, & J. N. Towse (Eds.), Variation in working memory (pp. 21–48). New York, NY: Oxford University Press.
Kane, M. J., & Engle, R. W. (2002). The role of prefrontal cortex in working-memory capacity, executive attention, and general fluid intelligence: An individual-differences perspective. Psychonomic Bulletin and Review, 9, 637–671. doi:10.3758/BF03196323
Kane, M. J., & Engle, R. W. (2003). Working-memory capacity and the control of attention: The contributions of goal neglect, response competition, and task set to Stroop interference. Journal of Experimental Psychology: General, 132, 47–70. doi:10.1037/0096-3445.132.1.47
Kane, M. J., Hambrick, D. Z., Tuholski, S. W., Wilhelm, O., Payne, T. W., & Engle, R. W. (2004). The generality of working memory capacity: A latent-variable approach to verbal and visuospatial memory span and reasoning. Journal of Experimental Psychology: General, 133, 189–217. doi:10.1037/0096-3445.133.2.189
Kessler, Y., & Meiran, N. (2008). Two dissociable updating processes in working memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 34, 1339–1348. doi:10.1037/a0013078
Kray, J., Eber, J., & Karbach, J. (2008). Verbal self-instructions in task switching: A compensatory tool for action-control deficits in childhood and old age? Developmental Science, 11, 223–236.
Kumaran, D., & Maguire, E. A. (2007). Which computational mechanisms operate in the hippocampus during novelty detection? Hippocampus, 17, 735–748.
Lakoff, G., & Johnson, M. (1980). Metaphors we live by. Chicago, IL: University of Chicago Press.
Lawrence, B. M., Myerson, J., Oonk, H. M., & Abrams, R. A. (2001). The effects of eye and limb movements on working memory. Memory, 9, 433–444.
Lewandowsky, S., Brown, G. D. A., & Thomas, J. L. (2009). Traveling economically through memory space: Characterizing output order in memory for serial order. Memory & Cognition, 37, 181–193. doi:10.3758/MC.37.2.181
Lewandowsky, S., & Farrell, S. (2008a). Phonological similarity in serial recall: Constraints on theories of memory. Journal of Memory and Language, 58, 429–448. doi:10.1016/j.jml.2007.01.005
Lewandowsky, S., & Farrell, S. (2008b). Short-term memory: New data and a model. In B. H. Ross (Ed.), The psychology of learning and motivation: Advances in research and theory (Vol. 49, pp. 1–48). San Diego, CA: Elsevier Academic Press.
Lewandowsky, S., & Farrell, S. (2011). Computational modeling in cognition: Principles and practice. Thousand Oaks, CA: Sage.
Lewandowsky, S., Geiger, S. M., Morrell, D. B., & Oberauer, K. (2010). Turning simple span into complex span: Time for decay or interference from distractors? Journal of Experimental Psychology: Learning, Memory, and Cognition, 36, 958–978. doi:10.1037/a0019764
Lewandowsky, S., Geiger, S. M., & Oberauer, K. (2008). Interference-based forgetting in short-term memory. Journal of Memory and Language, 59, 200–222.
Lewandowsky, S., Oberauer, K., & Brown, G. D. A. (2009). No temporal decay in verbal short-term memory. Trends in Cognitive Sciences, 13, 120–126. doi:10.1016/j.tics.2008.12.003
Lewis-Peacock, J. A., Drysdale, A. T., Oberauer, K., & Postle, B. R. (2011). Neural evidence for a distinction between short-term memory and the focus of attention. Journal of Cognitive Neuroscience, 24, 61–79.
Liefooghe, B., Barrouillet, P., Vandierendonck, A., & Camos, V. (2008). Working memory costs of task switching. Journal of Experimental Psychology: Learning, Memory, and Cognition, 34, 478–494. doi:10.1037/0278-7393.34.3.478
Logan, G. D. (1988). Toward an instance theory of automatization. Psychological Review, 95, 492–527. doi:10.1037/0033-295X.95.4.492
McCabe, D. (2008). The role of covert retrieval in working memory span tasks: Evidence from delayed recall tests. Journal of Memory and Language, 58, 480–494.
McCabe, J., & Hartman, M. (2003). Examining the locus of age effects on complex span tasks. Psychology and Aging, 18, 562–572.
McElree, B. (2001). Working memory and the focus of attention. Journal of Experimental Psychology: Learning, Memory, and Cognition, 27, 817–835.
McElree, B. (2006). Accessing recent events. In B. H. Ross (Ed.), The psychology of learning and motivation: Advances in research and theory (Vol. 46, pp. 155–200). San Diego, CA: Academic Press.
Mongillo, G., Barak, O., & Tsodyks, M. (2008). Synaptic theory of working memory. Science, 319, 1543–1546. doi:10.1126/science.1150769
Moyer, R., Bradley, D. R., Sorensen, M. H., Whiting, J. C., & Mansfield, D. P. (1978). Psychophysical functions for perceived and rememberedsize. Science, 200, 330–332.
Murray, D. J. (1967). The role of speech responses in short-term memory. Canadian Journal of Psychology, 21, 263–276.
Myerson, J., Hale, S., Rhee, S. H., & Jenkins, L. (1999). Selective interference with verbal and spatial working memory in young and older adults. Journals of Gerontology, 54B, P161–P164.
Nairne, J. S. (1990). A feature model of immediate memory. Memory & Cognition, 18, 251–269. doi:10.3758/BF03213879
Nairne, J. S. (2002). Remembering over the short-term: The case against the standard model. Annual Review of Psychology, 53, 53–81. doi:10.1146/annurev.psych.53.100901.135131
O’Reilly, R. C., & Frank, M. J. (2005). Making working memory work: A computational model of learning in the prefrontal cortex and the basal ganglia. Neural Computation, 18, 283–328.
Oberauer, K. (2001). Removing irrelevant information from working memory: A cognitive aging study with the modified Sternberg task. Journal of Experimental Psychology: Learning, Memory, and Cognition, 27, 948–957. doi:10.1037/0278-7393.27.4.948
Oberauer, K. (2002). Access to information in working memory: Exploring the focus of attention. Journal of Experimental Psychology: Learning, Memory, and Cognition, 28, 411–421. doi:10.1037/0278-7393.28.3.411
Oberauer, K. (2003a). Selective attention to elements in working memory. Experimental Psychology, 50, 257–269.
Oberauer, K. (2003b). Understanding serial position curves in short-term recognition and recall. Journal of Memory and Language, 49, 469–483.
Oberauer, K. (2005a). Binding and inhibition in working memory: Individual and age differences in short-term recognition. Journal of Experimental Psychology: General, 134, 368–387. doi:10.1037/0096-3445.134.3.368
Oberauer, K. (2005b). Control of the contents of working memory—A comparison of two paradigms and two age groups. Journal of Experimental Psychology: Learning, Memory, and Cognition, 31, 714–728. doi:10.1037/0278-7393.31.4.714
Oberauer, K. (2009). Design for a working memory. In B. H. Ross (Ed.), The psychology of learning and motivation: Advances in research and theory (Vol. 51, pp. 45–100). San Diego: Elsevier Academic Press. doi:10.1016/S0079-7421(09)51002-X
Oberauer, K., Farrell, S., Jarrold, C., Pasiecznik, K., & Greaves, M. (2012). Interference between maintenance and processing in working memory: The effect of item–distractor similarity in complex span. Journal of Experimental Psychology: Learning. Memory, and Cognition, 38, 665–685. doi:10.1037/a0026337
Oberauer, K., & Kliegl, R. (2006). A formal model of capacity limits in working memory. Journal of Memory and Language, 55, 601–626.
Oberauer, K., & Lewandowsky, S. (2008). Forgetting in immediate serial recall: Decay, temporal distinctiveness, or interference? Psychological Review, 115, 544–576. doi:10.1037/0033-295X.115.3.544
Oberauer, K., & Lewandowsky, S. (2011). Modeling working memory: A computational implementation of the Time-Based Resource-Sharing theory. Psychonomic Bulletin & Review, 18, 10–45. doi:10.3758/s13423-010-0020-6
Oberauer, K., Süß, H.-M., Schulze, R., Wilhelm, O., & Wittmann, W. W. (2000). Working memory capacity—Facets of a cognitive ability construct. Personality and Individual Differences, 29, 1017–1045.
Oberauer, K., & Vockenberg, K. (2009). Updating of working memory: Lingering bindings. Quarterly Journal of Experimental Psychology, 62, 967–987.
Page, M. P. A., & Norris, D. (1998). The primacy model: A new model of immediate serial recall. Psychological Review, 105, 761–781. doi:10.1037/0033-295X.105.4.761-781
Page, M. P. A., & Norris, D. (2009). A model linking immediate serial recall, the Hebb repetition effect and the learning of phonological word forms. Philosophical Transactions of the Royal Society B, 364, 3737–3753. doi:10.1098/rstb.2009.0173
Pashler, H. (1994). Dual-task interference in simple tasks: Data and theory. Psychological Bulletin, 116, 220–244. doi:10.1037/0033-2909.116.2.220
Peterson, L. R., & Peterson, M. J. (1959). Short-term retention of individual verbal items. Journal of Experimental Psychology, 58, 193–198.
Phaf, R. H., & Wolters, G. (1993). Attentional shifts in maintenance rehearsal. American Journal of Psychology, 106, 353–382.
Pollack, I., Johnson, L. B., & Knaff, P. R. (1959). Running memory span. Journal of Experimental Psychology, 57, 137–146.
Portrat, S., Barrouillet, P., & Camos, V. (2008). Time-related decay or interference-based forgetting in working memory? Journal of Experimental Psychology: Learning, Memory, and Cognition, 34, 1561–1564. doi:10.1037/a0013356
Portrat, S., Camos, V., & Barrouillet, P. (2009). Working memory in children: A time-constrained functioning similar to adults. Journal of Experimental Child Psychology, 102, 368–374. doi:10.1016/j.jecp. 2008.05.005
Posner, M. I., & Konick, A. W. (1966). On the role of interference in short-term retention. Journal of Experimental Psychology, 72, 221–231.
Ratcliff, R., Thapar, A., & McKoon, G. (2004). A diffusion model analysis of the effects of aging on recognition memory. Journal of Memory and Language, 50, 408–424.
Ratcliff, R., Thapar, A., & McKoon, G. (2010). Individual differences, aging, and IQ in two-choice tasks. Cognitive Psychology, 60, 127–157. doi:10.1016/j.cogpsych.2009.09.001
Rouder, J. N., Morey, R. D., Cowan, N., Zwilling, C. E., Morey, C. C., & Pratte, M. S. (2008). An assessment of fixed-capacity models of visual working memory. Proceedings of the National Academy of Sciences, 105, 5975–5979.
Saito, S., & Miyake, A. (2004). On the nature of forgetting and the processing-storage relationship in reading span performance. Journal of Memory and Language, 50, 425–443.
Saults, J. S., & Cowan, N. (2007). A central capacity limit to the simultaneous storage of visual and auditory arrays in working memory. Journal of Experimental Psychology: General, 136, 663–684. doi:10.1037/0096-3445.136.4.663
Schmiedek, F., Hildebrandt, A., Lövdén, M., Wilhelm, O., & Lindenberger, U. (2009). Complex span versus updating tasks of working memory: The gap is not that deep. Journal of Experimental Psychology: Learning, Memory, and Cognition, 35, 1089–1096. doi:10.1037/a0015730
Schweickert, R. (1993). A multinomial processing tree model for degradation and redintegration in immediate recall. Memory & Cognition, 21, 168–173.
Shah, P., & Miyake, A. (1996). The separability of working memory resources for spatial thinking and language processing: An individual differences approach. Journal of Experimental Psychology: General, 125, 4–27. doi:10.1037/0096-3445.125.1.4
Tehan, G., & Humphreys, M. S. (1995). Transient phonemic codes and immunity to proactive interference. Memory & Cognition, 23, 181–191.
Towse, J. N., Hitch, G. J., & Hutton, U. (2000). On the interpretation of working memory span in adults. Memory & Cognition, 28, 341–348.
Turner, M. L., & Engle, R. W. (1989). Is working memory capacity task dependent? Journal of Memory and Language, 28, 127–154.
Unsworth, N. (2010). On the division of working memory and long-term memory and their relation to intelligence: A latent variable approach. Acta Psychologica, 134, 16–28. doi:10.1016/j.actpsy.2009.11.010
Unsworth, N., Brewer, G. A., & Spillers, G. J. (2009). There’s more to the working memory–Fluid intelligence relationship than just secondary memory. Psychonomic Bulletin & Review, 16, 931–937. doi:10.3758/PBR.16.5.931
Unsworth, N., & Engle, R. W. (2005). Individual differences in working memory capacity and learning: Evidence from the serial reaction time task. Memory & Cognition, 33, 213–220. doi:10.3758/BF03195310
Unsworth, N., & Engle, R. W. (2006). A temporal-contextual retrieval account of complex span: An analysis of errors. Journal of Memory and Language, 54, 346–362.
Unsworth, N., & Engle, R. W. (2007). The nature of individual differences in working memory capacity: Active maintenance in primary memory and controlled search from secondary memory. Psychological Review, 114, 104–132. doi:10.1037/0033-295X.114.1.104
Unsworth, N., Schrock, J. C., & Engle, R. W. (2004). Working memory capacity and the antisaccade task: Individual differences in voluntary saccade control. Journal of Experimental Psychology: Learning, Memory, and Cognition, 30, 1302–1321. doi:10.1037/0278-7393.30.6.1302
Vergauwe, E., Barrouillet, P., & Camos, V. (2010). Do mental processes share a domain-general resource? Psychological Science, 21, 384–390. doi:10.1177/0956797610361340
Verguts, T., & Notebaert, W. (2008). Hebbian learning of cognitive control: Dealing with specific and nonspecific adaptation. Psychological Review, 115, 518–525. doi:10.1037/0033-295X.115.2.518
Vogel, E. K., McCollough, A. W., & Machizawa, M. G. (2005). Neural measures reveal individual differences in controlling access to working memory. Nature, 438, 500–503. doi:10.1038/nature04171
Vogel, E. K., Woodman, G. F., & Luck, S. J. (2006). The time course of consolidation in visual working memory. Journal of Experimental Psychology: Human Perception and Performance, 32, 1436–1451. doi:10.1037/0096-1523.32.6.1436
Wylie, G. R., Foxe, J. J., & Taylor, T. T. (2007). Forgetting as an active process: An fMRI investigation of item-method-directed forgetting. Cerebral Cortex, 18, 670–682.
Yntema, D. B., & Mueser, G. E. (1962). Keeping track of variables that have few or many states. Journal of Experimental Psychology, 63, 391–395.
Author note
K.O., S.F., and C.J. were supported by Grant RES-062-23-1199 from the Economic and Social Research Council (ESRC). S.L. was supported by a Discovery Grant from the Australian Research Council (ARC) and an Australian Professorial Fellowship. The help of Charles Hanich with collecting the data is greatly appreciated.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Oberauer, K., Lewandowsky, S., Farrell, S. et al. Modeling working memory: An interference model of complex span. Psychon Bull Rev 19, 779–819 (2012). https://doi.org/10.3758/s13423-012-0272-4
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13423-012-0272-4