Skip to main content
SpringerLink
Log in

Determination of Interference Invariants in a Deep-Water Waveguide by Amplitude and Phase Methods

  • HYDRODYNAMICS AND UNDERWATER ACOUSTICS
  • Published:
Physics of Wave Phenomena Aims and scope Submit manuscript

Abstract—

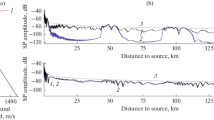
It is established that the interference invariant can be calculated not only by analyzing the frequency and spatial distribution of the intensity field but also by studying the phase-gradient field. It is found that the interference structure of the intensity field and the field of value inverse to the phase gradient (effective phase velocity) can be described by identical dependences, based on the use of invariant. It is shown that, in contrast to shallow water, which is characterized by relative stability of invariant values, the interference invariant in deep water changes significantly with variation in distance. In the shadow zone, with detectors and sources located at real depths (less than 400 m), the interference invariant can be described by an analytical dependence, which is in essence affected by only the water depth and distance; it is affected by neither sound frequency, nor source depth, nor detector depth and is only slightly affected by the characteristics of speed-of-sound vertical profile. Hence, the thus obtained analytical dependence can be referred to as invariant.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.

Similar content being viewed by others

REFERENCES

  1. S. D. Chuprov, “Interference structure of a sound field in a layered ocean,” in Ocean Acoustics, Current Status, Ed. by L. M. Brekhovskikh and I. B. Andreyeva (Nauka, Moscow, 1982), pp. 71–91 [in Russian].

    Google Scholar 

  2. L. M. Brekhovskikh and Yu. P. Lysanov, Theoretical Foundations of Ocean Acoustics (Nauka, Moscow, 2007) [in Russian].

    MATH  Google Scholar 

  3. K. L. Cockrell and H. Schmidt, “A modal Wentzel–Kramers–Brillouin approach to calculating the waveguide invariant for non-ideal waveguides,” J. Acoust. Soc. Am. 130 (1), 72–83 (2011). https://doi.org/10.1121/1.3592236

    Article  ADS  Google Scholar 

  4. G. A. Grachev, “On theory of acoustic field invariants in layered waveguides,” Acoust. Phys. 39 (1), 33–35 (1993).

    ADS  Google Scholar 

  5. A. M. Thode, W. A. Kuperman, G. L. D’Spain, and W. S. Hodgkiss, “Localization using Barlett matched-field processor sidelobes,” J. Acoust. Soc. Am. 107 (1), 278–286 (2000). https://doi.org/10.1121/1.428304

    Article  ADS  Google Scholar 

  6. V. M. Kuz’kin, Yu. V. Matvienko, S. A. Pereselkov, and E. S. Kaznacheeva, “Interferometric processing by using a vertical linear antenna,” Vestn. Voronezh Gos. Univ. Ser. Fiz. Matem. No. 2, 14–23 (2020).

    Google Scholar 

  7. H. C. Song and Gihoon Byun, “Extrapolating Green’s functions using the waveguide invariant theory,” J. Acoust. Soc. Am. 147 (4), 2150–2158 (2020). https://doi.org/10.1121/10.0000969

    Article  ADS  Google Scholar 

  8. Qian-Qian Li, Zheng-Lin Li, and Ren-He Zhang, “Applications of waveguide invariant theory to the analysis of interference phenomena in deep water,” Chin. Phys. Lett. 28 (3), 034303 (2011). https://doi.org/10.1088/0256-307X/28/3/034303

    Article  ADS  Google Scholar 

  9. R. Emmetiere, J. Bonnel, M. Géhant, X. Cristol, and T. Chonavel, “Understanding deep-water striation patterns and predicting the waveguide invariant as a distribution depending on range and depth,” J. Acoust. Soc. Am. 143 (6), 3444–3454 (2018). https://doi.org/10.1121/1.5040982

    Article  ADS  Google Scholar 

  10. G. A. Grachev and G. N. Kuznetsov, “Average rate of change of the phase of a sound field along a planer waveguide,” Sov. Phys.-Acoust. 31 (2), 154–156 (1985).

    Google Scholar 

  11. G. N. Kuznetsov and O. V. Lebedev, “The possibility of using the equivalent plane wave model to increase the efficiency of taking bearings of low-frequency signals in shallow water,” Acoust. Phys. 58 (5), 575 (2012). https://doi.org/10.1134/S1063771012030098

    Article  ADS  Google Scholar 

  12. S. P. Aksenov and G. N. Kuznetsov, “Invariance of the effective phase velocity of a hydroacoustic field in the deep ocean,” Dokl. Phys. 65 (7), 261–264 (2020). https://doi.org/10.1134/S1028335820050043

    Article  ADS  Google Scholar 

  13. G. N. Kuznetsov, O. V. Lebedev, and A. N. Stepanov, “Vertical amplitude phase structure of a low-frequency acoustic field in shallow water,” Acoust. Phys. 62 (6), 717–728 (2016). https://doi.org/10.1134/S1063771016050092

    Article  ADS  Google Scholar 

  14. A. K. Novikov, Correlation Measurements in Ship Acoustics (Sudostroenie, Leningrad, 1971) [in Russian].

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Prokhorov General Physics Institute of the Russian Academy of Sciences, 119991, Moscow, Russia

    S. P. Aksenov & G. N. Kuznetsov

Authors
  1. S. P. Aksenov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. N. Kuznetsov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. N. Kuznetsov.

Additional information

Translated by Yu. Sin’kov

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Aksenov, S.P., Kuznetsov, G.N. Determination of Interference Invariants in a Deep-Water Waveguide by Amplitude and Phase Methods. Phys. Wave Phen. 29, 81–87 (2021). https://doi.org/10.3103/S1541308X21010015

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S1541308X21010015

Keywords:

Search

Navigation