Skip to main content
SpringerLink
Log in

Speed Stabilization of Mechatronic Systems of Interval Type

  • Published:
Russian Engineering Research Aims and scope

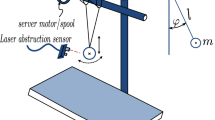
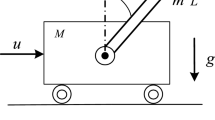
Abstract

A method is proposed for adjusting the regulators of dynamic quadratic systems in which the state variables influence one another, with retardation of the kinematic deviations from the reference (program) trajectory, in the case where the parameters are integrally indeterminate. This approach is based on decomposition of the initial system and the direct Lyapunov method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.

Similar content being viewed by others

REFERENCES

  1. Asanov, A.Z. and Dem’yanov, D.N., Choice of the optimal structure of the output matrix during changing the spectrum of transfer zeros of a multiply connected dynamic system, Vestn. Ufimsk. Gos. Aviats. Tekh. Univ., 2009, vol. 13, no. 2 (35), pp. 11–17.

  2. Lizina, E.A. and Shchennikov, V.N., Stabilization of a multiply-connected controlled hybrid dynamic system with non-overlapping decompositions, Izv. Vyssh. Uchebn. Zaved., Povolzh. Reg., Fiz.-Mat. Nauki, 2011, no. 4 (20), pp. 14–23.

  3. Stebulyanin, M.M., The decomposition method in the stability analysis of a multi-connected mechatronic system, Vestn. Mosk. Gos. Tekhnol. Univ., Stankin, 2008, no. 4, pp. 39–44.

  4. Stebulyanin, M.M., The synthesis of stabilizers of mechatronic systems within parametric uncertainty, Vestn. Mosk. Gos. Tekhnol. Univ., Stankin, 2016, no. 4 (39), pp. 90–93.

  5. Lizina, E.A. and Shchennikova, E.V., Stabilization of a multi-connected continuously-discrete non-autonomous system, Vestn. Mordovsk. Univ., Fiz.-Mat. Nauki, 2012, no. 2, pp. 98–103.

  6. Pshikhonov, V.Kh. and Medvedev, M.Yu., Synthesis of control systems for submerged vehicles with nonlinear characteristics of executive bodies, Izv. Yuzhn. Fed. Univ., Tekh. Nauki, 2011, no. 3 (116), pp. 147–156.

  7. Stebulyanin, M.M. and Sinitsyn, A.G., The principle of contour control by an industrial robot in the mode of technological uncertainty, Vestn. Mosk. Gos. Tekhnol. Univ., Stankin, 2011, no. 3 (15), pp. 161–163.

  8. Makarova, T.A. and Stebulyanin, M.M., Robust algorithm for stabilization of the movement of a three-link robot with a gearless drive, Vestn. Mosk. Gos. Tekhnol. Univ., Stankin, 2013, no. 2 (25), pp. 74–79.

  9. Lezhnina, Yu.A. and Ternovaya, G.N., Robust decentralized control with compensation of disturbances by nonlinear multi-connected objects with state delay, Vestn. Astrakh. Gos. Tekh. Univ., Ser.: Upr., Vychisl. Tekh. Inf., 2012, no. 2, pp. 47–55.

  10. Stebulyanin, M.M., The derivation of the equations of perturbed motion of the class of mechatronic systems, Vestn. Mosk. Gos. Tekhnol. Univ., Stankin, 2011, no. 3 (15), pp. 131–136.

  11. Zimenko, K.A., Kremlev, A.S., Polyakov, A.E., and Efimov, D.V., Robust stabilization of a two-rotor multichannel object, Nauchn.-Tekh. Vestn. Inf. Tekhnol., Mekh. Opt., 2018, vol. 18, no. 3, pp. 392–398.

    Google Scholar 

  12. Kalyadin, V.A. and Stebulyanin, M.M., Dynamic model of a doubly coupled mechatronic system with elasticity and free play, Russ. Eng. Res., 2013, vol. 33, no. 6, pp. 372–374.

    Article  Google Scholar 

  13. Kravchenko, S.A., Nabilkin, A.Yu., and Biryukov, V.P., Multiconnected control system of cutting force and the position of the cutter along the transverse axis, Vestn. Sarat. Gos. Tekh. Univ., 2011, no. 3 (58), pp. 202–205.

  14. Kirillov, A.N., Dynamic decomposition method in modeling of control systems with structural changes, Inf.-Upr. Sist., 2009, no. 1, pp. 20–24.

  15. Rodionov, V.I., Decomposition and research method of gyroscopic systems based on the guidance-stabilization principle, Izv. Tul’sk. Gos. Univ., Tekh. Nauki, 2016, no. 10, pp. 301–310.

  16. Eshenko, A.A., Synthesis of automatic control devices of a doubly-connected control system for servo-drives of manipulators, Sovrem. Tekhnol. Sist. Anal. Model., 2014, no. 1 (41), pp. 76–83.

  17. Aleksandrov, A.Yu. and Kosov, A.A., Stability analysis of equilibrium positions of nonlinear mechanical systems based on decomposition, Vestn. S.-Peterb. Univ., Ser. 10: Prikl. Matem. Inf. Protsess. Upr., 2009, no. 1, pp. 143–154.

  18. Stebulyanin, M.M., Combinated synthesis of the law of control of multiconnected mechatronic systems in dynamic positioning mode, Mekhatronika, Avtom., Upr., 2009, no. 10, pp. 31–35.

Download references

Author information

Authors and Affiliations

  1. Stankin Moscow State Technical University, Moscow, Russia

    M. M. Stebulyanin & A. V. Malyarenko

Authors
  1. M. M. Stebulyanin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. V. Malyarenko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. M. Stebulyanin.

Additional information

Translated by B. Gilbert

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Stebulyanin, M.M., Malyarenko, A.V. Speed Stabilization of Mechatronic Systems of Interval Type. Russ. Engin. Res. 39, 1001–1007 (2019). https://doi.org/10.3103/S1068798X19120219

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S1068798X19120219

Keywords:

Search

Navigation