Skip to main content
SpringerLink
Log in

A data assimilation technique based on the π-algorithm

  • Published:
Russian Meteorology and Hydrology Aims and scope Submit manuscript

Abstract

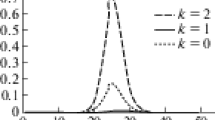
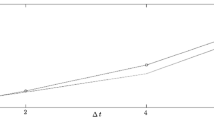
A practical implementation of the data assimilation algorithm based on the Kalman filter in its complete formulation is impossible due to high dimension of the associated equation sets and to nonlinearity of the predicted processes. The main direction in the implementation of the Kalman filter is an ensemble approach. Under the assumption of ergodicity of random forecast errors, an alternative algorithm with respect to the ensemble Kalman filter can be considered, in which probability averaging is replaced by time averaging. The proposes algorithm is based this assumption. The algorithm is easy to implement; however, its convergence, applicability to the data assimilation problems, and connection to the Kalman filter have not been studied. In the paper, applicability of the π-algorithm to data assimilation is considered on an example of a simple one-dimensional advection equation. Use of this simple equation allows comparing the classical Kalman filter algorithm with various practical approaches to its implementation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. V. Balakrishnan, Kalman Filtering Theory (Mir, Moscow, 1988) [in Russian].

    Google Scholar 

  2. E. G. Klimova, “Algorithm for Data Assimilation Based on Adaptive Suboptimum Kalman Filter,” Meteorol. Gidrol., No. 3 (2005) [Russ. Meteorol. Hydrol., No. 3 (2005)].

  3. E. G. Klimova, “An Asymptotic Behavior of Meteorological Data Assimilation Scheme Based on the Kalman Filter Algorithm,” Meteorol. Gidrol., No. 8 (1999) [Russ. Meteorol. Hydrol., No. 8 (1999)].

  4. E. G. Klimova, “The Algorithm of Meteorological Data Assimilation Based on the Extended Suboptimal Kalman Filter,” Meteorol. Gidrol., No. 11 (1997) [Russ. Meteorol. Hydrol., No. 11 (1997)].

  5. E. G. Klimova, “A Model to Calculate the Covariance of Homogeneous Isotropic Stochastic Fields of Forecast Errors,” Meteorol. Gidrol., No. 10 (2001) [Russ. Meteorol. Hydrol., No. 10 (2001)].

  6. E. G. Klimova, “A Primitive-Equation Model for Calculation of Forecast Error Covariances in the Kalman Filter Algorithm,” Meteorol. Gidrol., No. 11 (2001) [Russ. Meteorol. Hydrol., No. 11 (2001)].

  7. E. G. Klimova, “Simplified Models of Computation of the Covariance Matrices in the Kalman Filter Algorithm,” Meteorol. Gidrol., No. 6 (2000) [Russ. Meteorol. Hydrol., No. 6 (2000)].

  8. E. G. Klimova, “Numerical Experiments on Meteorological Data Assimilation Using a Suboptimal Kalman Filter,” Meteorol. Gidrol., No. 10 (2003) [Russ. Meteorol. Hydrol., No. 10 (2003)].

  9. A. A. Krasovskii, I. N. Beloglazov, and G. P. Chigin, Theory of Correlation-extreme Navigation Systems (Nauka, Moscow, 1979) [in Russian].

    Google Scholar 

  10. D. M. Sonechkin, “Dynamical-statistical Approach to the Problem of Objective Analysis of Heterogeneous Meteorological Observations,” Trudy Gidromettsentra SSSR, No. 181 (1976) [Trans. Hydrometeorological Res. Center of the USSR, No. 181 (1976)].

  11. Reference Book on Automated Control, Ed. by A.A. Krasovskii (Nauka, Moscow, 1987) [in Russian].

    Google Scholar 

  12. A. M. Yaglom, Correlation Theory of Stationary Random Functions (Gidrometeoizdat, Leningrad, 1981) [in Russian].

    Google Scholar 

  13. M. Fisher and E. Andersson, Development in 4D-Var and Kalman Filtering, Technical Memorandum No. 357 (ECMWF, Reading, England, 2001).

    Google Scholar 

  14. A. H. Jazwinski, Stochastic Processes and Filtering Theory (Academic Press, New York, 1970).

    Google Scholar 

  15. P. L. Houtekamer and H. L. Mitchell, “Data Assimilation Using an Ensemble Kalman Filter Technique,” Mon. Wea. Rev., 126 (1998).

  16. P. L. Houtekamer and H. L. Mitchell, “Ensemble Kalman Filtering,” Quart. J. Roy. Meteorol. Soc., 131 (2005).

  17. M. Ghil and P. Malanotte-Rizzolli, “Data Assimilation in Meteorology and Oceanography,” Adv. Geophys., 33 (1991).

  18. E. Kalnay, B. R. Hunt, E. J. Kostelich, et al., “Four-dimensional Ensemble Kalman Filtering,” Tellus, 56A (2004).

  19. F. Rabier, P. Courtier, J. Pailleux, et al., “Comparison of Four-dimensional Variational Assimilation with Simplified Sequential Assimilation,” in Proc. of ECMWF Workshop “Variational Assimilation, with Special Emphasis on Three-Dimensional Aspects,” November 9–12, 1992.

  20. O. Talagrand and P. Courtier, “Variational Assimilation of Meteorological Observations with the Adjoint Vorticity Equation. I: Theory,” Quart. J. Roy. Meteorol. Soc., 113 (1987).

  21. R. Todling and S. Cohn, “Suboptimal Schemes for Atmospheric Data Assimilation Based on the Kalman Filter,” Mon. Wea. Rev., 124 (1996).

Download references

Author information

Authors and Affiliations

  1. Institute for Computational Technologies, Siberian Division, Russian Academy of Sciences, pr. Lavrent’eva 6, Novosibirsk, 630090, Russia

    E. G. Klimova

Authors
  1. E. G. Klimova
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Original Russian Text © E.G. Klimova, 2008, published in Meteorologiya i Gidrologiya, 2008, No. 3, pp. 16–26.

About this article

Cite this article

Klimova, E.G. A data assimilation technique based on the π-algorithm. Russ. Meteorol. Hydrol. 33, 143–150 (2008). https://doi.org/10.3103/S1068373908030023

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S1068373908030023

Keywords

Search

Navigation