Skip to main content
SpringerLink
Log in

Cardinal splines in nonparametric regression

  • Published:
Mathematical Methods of Statistics Aims and scope Submit manuscript

Abstract

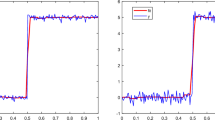
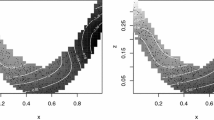
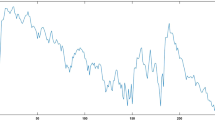
We discuss a nonparametric regression model on an equidistant grid of the real line. A class of kernel type estimates based on the so-called fundamental cardinal splines will be introduced. Asymptotic optimality of these estimates will be established for certain functional classes. This model explains the often mentioned heuristic fact that cubic splines are adequate for most practical applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. N. I. Akhiezer, Theory of Approximation (Frederick Ungar Publ., New York, 1956).

    MATH  Google Scholar 

  2. L. Artiles and B. Levit, “Adaptive Regression on the Real Line in Classes of Smooth Functions”, Austrian J. Statist. 32, 99–129 (2003).

    Google Scholar 

  3. R. L. Eubank, Spline Smoothing and Nonparametric Regression, 2nd ed. (Marcel Dekker, New York, 1999).

    MATH  Google Scholar 

  4. W. Feller, An Introduction to Probability Theory and Its Applications, (Wiley, New York, 1966), Vol. II.

    MATH  Google Scholar 

  5. O. Lepski and B. Levit, “Adaptive Minimax Estimation of Infinitely Differentiable Functions”, Math. Methods Statist. 7, 123–156 (1998).

    MATH  MathSciNet  Google Scholar 

  6. M. J. Marsden, F. B. Richards, and S. D. Riemenschneider, “Cardinal Spline Interpolation Operators on l p Data”, J. Math., Indiana Univ. 24, 667–689 (1975).

    Google Scholar 

  7. C. A. Micchelli, “Infinite Spline Interpolation”, in Approximation in Theorie and Praxis (Bibliographisches Institute, Mannheim, 1979), pp. 209–238.

    Google Scholar 

  8. M. Reimer, “The Main Roots of the Euler-Frobenius Polynomials”, J. Approximation Theory 45, 358–362 (1985).

    Article  MATH  MathSciNet  Google Scholar 

  9. I. J. Schoenberg, Cardinal Spline Interpolation (SIAM, New York, 1973).

    MATH  Google Scholar 

  10. I. J. Schoenberg, “Cardinal Interpolation and Spline Functions, II”, J. Approximation Theory 6, 404–420 (1974).

    Article  MathSciNet  Google Scholar 

  11. I. J. Schoenberg, Selected Papers, Ed. by Carl de Boor (Birkhäuser, Boston, 1988).

    Google Scholar 

  12. I. J. Schoenberg and A. Sharma, “The Interpolatory Background of the Maclaurin Quadrature Formula”, Bull. Amer. Math. Soc. 77, 1034–1038 (1971).

    Article  MATH  MathSciNet  Google Scholar 

  13. L. L. Schumaker, Spline Functions: Basic Theory (Wiley, New York, 1981).

    MATH  Google Scholar 

  14. E. C. Titchmarsh, Introduction to the Theory of Fourier Integrals (Oxford Univ. Press, Oxford, 1962).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dept. of Statistics, Seoul National University, Seoul, Korea

    J. Cho

  2. Dept. of Mathematics and Statistics, Queen’s University, Kingston, ON, Canada

    B. Levit

Authors
  1. J. Cho
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. B. Levit
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to B. Levit.

About this article

Cite this article

Cho, J., Levit, B. Cardinal splines in nonparametric regression. Math. Meth. Stat. 17, 19–34 (2008). https://doi.org/10.3103/S106653070801002X

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S106653070801002X

Key words

2000 Mathematics Subject Classification

Search

Navigation