Skip to main content
SpringerLink
Log in

Lebesgue functions corresponding to a family of Lagrange interpolation polynomials

  • Published:
Russian Mathematics Aims and scope Submit manuscript

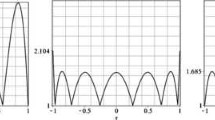
Abstract

In this paper we obtain various explicit forms of the Lebesgue function corresponding to a family of Lagrange interpolation polynomials defined at an even number of nodes. We study these forms by using the derivatives up to the second order inclusive. We estimate exact values of Lebesgue constants for this family from below and above in terms of known parameters. In a particular case we obtain new convenient formulas for calculating these estimates.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. Zygmund, Trigonometrical Series (Warszawa-Lwow, 1935; Mir, Moscow, 1965), Vol. 2.

    Google Scholar 

  2. I. A. Shakirov, “The Lagrange Trigonometric Interpolation Polynomial With the Minimal Norm Considered as an Operator from {ie76-1},” Izv. Vyssh. Uchebn. Zaved. Mat., No. 10, 60–68 (2010) [Russian Mathematics (Iz. VUZ) 54 (10), 52–59 (2010)].

    Google Scholar 

  3. I. A. Shakirov, “A Complete Description of the Lebesgue Functions for Classical Lagrange Interpolation Polynomials,” Izv. Vyssh. Uchebn. Zaved. Mat., No. 10, 80–88 (2011) [Russian Mathematics (Iz. VUZ) 55 (10), 70–77 (2011)].

    Google Scholar 

  4. N. P. Korneichuk, Sharp Constants in Approximation Theory (Nauka, Moscow, 1987) [in Russian].

    Google Scholar 

  5. V. K. Dzyadyk, Approximation Methods for Solutions of Differential and Integral Equations (Naukova Dumka, Kiev, 1988) [in Russian].

    Google Scholar 

  6. Yu. N. Subbotin and S. A. Telyakovskii, “Asymptotics of the Lebesgue Constants for Periodic Interpolation Splines on Uniform Grids,” Matem. Sborn. 191(8), 131–140 (2000).

    Article  MathSciNet  Google Scholar 

  7. K. I. Babenko, Principles of Numerical Analysis (NITs of Regular and Chaotic Dynamics, Moscow-Izhevsk, 2002) [in Russian].

    Google Scholar 

  8. V. A. Kim, “Sharp Lebesgue Constants for Bounded Cubic Interpolation L-Splines,” Sib. Matem. Zhurn. 51(2), 330–341 (2010).

    Article  Google Scholar 

  9. N. V. Baidakova, “Lower Bound for the Lebesgue Function of an Interpolation Process with Algebraic Polynomials on Equidistant Nodes of a Simplex,” Matem. Zametki 92(1), 19–26 (2012).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Naberezhnye Chelny Institute of Social Pedagogical Technologies and Resources, 28 Nizametdinova str., Naberezhnye Chelny, 423806, Russia

    I. A. Shakirov

Authors
  1. I. A. Shakirov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to I. A. Shakirov.

Additional information

Original Russian Text © I.A. Shakirov, 2013, published in Izvestiya Vysshikh Uchebnykh Zavedenii. Matematika, 2013, No. 7, pp. 77–89.

About this article

Cite this article

Shakirov, I.A. Lebesgue functions corresponding to a family of Lagrange interpolation polynomials. Russ Math. 57, 66–76 (2013). https://doi.org/10.3103/S1066369X13070074

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S1066369X13070074

Keywords and phrases

Search

Navigation