Abstract
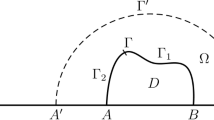
In this paper we consider an over-determined Cauchy problem for the Helmholtz equation in a semiinfinite domain with a piecewise smooth curvilinear boundary. Applying the Fourier transform method in the space of distributions of slow growth, we establish the necessary and sufficient solvability conditions which connect the boundary functions. We construct integral representations of a solution.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
B. Zhang and S. N. Chandler-Wilde, “Acoustic Scattering by an Inhomogeneous Layer on a Rigid Plate,” SIAM J. Appl.Math. 58(6), 1931–1950 (1998).
D. Colton and R. Kress, Integral Equations Methods in Scattering Theory (John Wiley & Sons, New York, 1983; Mir, Moscow, 1987).
A. Benali, J. Chandezon, and J. Fontaine, “A New Theory for Scattering of Electromagnetic Waves from Conducting or Dielectric Rough Surfaces,” IEEE Trans. Antennas and Propagation. 40, 141–148 (1992).
P. Cao and C. Macaskill, “Iterative Techniques for Rough Surface Scattering Problems,” Wave Motion 21, 209–229 (1995).
E. K. Lipachev, On an Approximation Solution of the Boundary Value Problem of Wave Diffraction on Domains with Infinite Boundary,” Izv. Vyssh. Uchebn. Zaved. Mat., No. 4, 69–72 (2001) [RussianMathematics (Iz. VUZ) 45 (4), 67–70 (2001)].
E. K. Lipachev, “On an Approximate Solution of a Boundary Value Problem of Wave Diffraction by Domains with an Infinite Boundary,” Preprint No. PMF-05-01 (Kazan Math. Soc., Kazan, 2005).
E. K. Lipachev, “Solution of the Dirichlet Problem for the Helmholtz Equation in Domains with a Rough Boundary,” Izv. Vyssh. Uchebn. Zaved.Mat., No. 9, 43–49 (2006). [RussianMathematics (Iz. VUZ) 50 (9), 41–46 (2006).
D. N. Tumakov, “Integral Equations of the Problem of Diffraction of ElectromagneticWaves on a Curvilinear Metal Screen,” in Proceeding of N. I. Lobachevskii Math. Center.’ Numerical Solution Methods for Linear and Nonlinear Boundary-Value Problems’ (Kazan Math. Soc., Kazan, 2001), Vol. 13, pp. 218–225 [in Russian].
V. S. Vladimirov, Equations of Mathematical Physics (Nauka, Moscow, 1971) [in Russian].
Yu. A. Brychkov and A. P. Prudnikov, Integral Transforms of Generalized Functions (Nauka, Moscow, 1977) [in Russian].
H. Honl, A. Maue, and K. Westphal, Diffraction Theory (Springer Göttingen, Heidelberg, Berlin, 1961; Mir, Moscow, 1964).
N. B. Pleshchinskii and D. N. Tumakov, “Boundary Value Problems for the Helmholtz Equation in a Quadrant and in a Half-Plane Formed from Two Quadrants,” Izv. Vyssh. Uchebn. Zaved. Mat., No. 7, 63–74 (2004) [Russian Mathematics (Iz. VUZ) 52 (7), 61–72 (2004).
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © D.N. Tumakov, 2010, published in Izvestiya Vysshikh Uchebnykh Zavedenii. Matematika, 2010, No. 2, pp. 77–85.
About this article
Cite this article
Tumakov, D.N. An over-determined boundary problem for the Helmholtz equation in a semiinfinite domain with a curvilinear boundary. Russ Math. 54, 66–73 (2010). https://doi.org/10.3103/S1066369X10020088
Received:
Published:
Issue Date:
DOI: https://doi.org/10.3103/S1066369X10020088