Skip to main content
SpringerLink
Log in

Multidimensional Signal Interpolation Based on Factorization and Dimension Reduction of Decision Rules

  • Published:
Optical Memory and Neural Networks Aims and scope Submit manuscript

Abstract

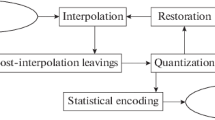
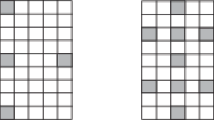
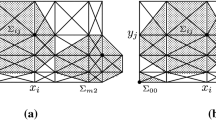
We research adaptive multidimensional signal interpolators based on switching between several interpolating functions at each signal sample. We perform the switching by decision rule, which is optimized for each signal in the parameter space of this decision rule. Algorithms for factorization and dimension reduction of decision rules are proposed. We investigate new classes of interpolating functions and systems of local features. We propose fitting procedures for adaptive interpolators. We perform the software implementation of the developed algorithms. A numerical experiment in natural multidimensional signals (video, remote sensing data and hyperspectral data) confirms the gain of the adaptive interpolator.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.

Similar content being viewed by others

REFERENCES

  1. Woods, J., Multidimensional Signal, Image, and Video Processing and Coding, Academic Press, 2011, 2th ed.

    Google Scholar 

  2. Yao, W., Video Processing and Communications, New York: Prentice Hall, 2002.

    Google Scholar 

  3. Borengasser, M., Hyperspectral Remote Sensing: Principles and Applications, New York: CRC Press, 2007.

    Book  Google Scholar 

  4. Lillesand, T., Remote Sensing and Image Interpretation, John Wiley & Sons, 2015, 7th ed.

    Google Scholar 

  5. Chang, C., Hyperspectral Data Exploitation: Theory and Applications, Wiley-Interscience, 2007.

    Book  Google Scholar 

  6. Vaganov, S.E. and Khashin, S.I., Comparison of doubling the size of image algorithms, Model. Anal. Inf. Sist., 2016, vol. 23, no. 4, pp. 382–400.

    Article  Google Scholar 

  7. Computer Image Processing, Part II: Methods and Algorithms, Soifer, V.A., Ed., VDM Verlag, 2010.

    Google Scholar 

  8. Li, X. and Orchard, M.T., New edge-directed interpolation, IEEE Trans. Image Process., 2001, vol. 10, no. 10, pp. 1521–1527.

    Article  Google Scholar 

  9. Gashnikov, M.V., Context interpolation of multidimensional digital signals in problem of compression, Opt. Mem. Neural Networks, 2018, vol. 27, no. 3, pp. 183–190.

    Article  Google Scholar 

  10. Zhou, D., Shen, X. and Dong, W., Image zooming using directional cubic convolution interpolation, IET Image Processing., 2012, vol. 6, no. 6, pp. 627–634.

    Article  MathSciNet  Google Scholar 

  11. Dong, C., Loy, C., He, K., and Tang, X., Image super-resolution using deep convolutional networks, IEEE Trans. Pattern Anal. Mach. Intell., 2016, vol. 38, no. 2, pp. 295–307.

    Article  Google Scholar 

  12. Eldar, Y.C., Compressed Sensing: Theory and Applications and Signal Processing, Cambridge University Press, 2012.

    Book  Google Scholar 

  13. Gonzalez, R.C., Digital Image Processing, Prentice Hall, 2007, 3th ed.

    Google Scholar 

  14. Gashnikov, M.V., A differential image compression method using adaptive parameterized extrapolation, Opt. Mem. Neural Networks, 2017, vol. 26, no. 2, pp. 137–144.

    Article  Google Scholar 

  15. Maksimov, A.I. and Gashnikov, M.V., Parameterization of the nonlinear interpolator invariant to four directions contours for multidimensional digital signals, CEUR Workshop Proc., 2018, vol. 2210, pp. 21–28.

    Google Scholar 

  16. Wu, S. and Lew, M., Image correspondences matching using multiple features fusion, Computer Vision – ECCV 2016 Workshops, 2016.

  17. Sayood, K., Introduction to Data Compression, Morgan Kaufmann Publishers, 2012, 4th ed.

    MATH  Google Scholar 

  18. Sergeev, V.V., Glumov, N.I., and Gashnikov, M.V., The informational technique of image compression in operative remote sensing systems, Izv. Samar. Nauchn. Tsentra. Ross. Akad. Nauk, 1999, no. 1, pp. 99–107.

  19. Glumov, N.I. and Gashnikov, M.V., Onboard processing of hyperspectral data in the remote sensing systems based on hierarchical compression, Comput. Opt., 2016, vol. 40, no. 4, pp. 543–551.

    Article  Google Scholar 

  20. Feichtenhofer, C., Pinz, A., and Wildes, R.P., Dynamic Scenes Data Set. http://vision.eecs.yorku.ca/research/dynamic-scenes.

  21. TokyoTech 31-band Hyperspectral Image Dataset. http://www.ok.sc.e.titech.ac.jp/res/MSI/MSIdata31.html.

  22. AVIRIS Data—Ordering Free AVIRIS Standard Data Products. Jet Propulsion Laboratory. http://aviris.jpl.nasa.gov/data/free_data.html.

  23. SpecTIR Data—Advanced Hyperspectral and Geospatial Solutions Corporate Headquarters SpecTIR Remote Sensing Division. http://www.spectir.com/free-data-samples.

Download references

Funding

The work was partly funded:

by RFBR according to the research project 18-01-00667 in parts of “1 Interpolator decision rule parameterization”—“8 Experimental study of the adaptive interpolator”;

by the Russian Federation Ministry of Science and Higher Education within a state contract with the “Crystallography and Photonics” Research Center of the RAS under agreement 007-ГЗ/Ч3363/26 in part of “Introduction”.

Author information

Authors and Affiliations

  1. Samara National Research University, 443086, Samara, Russia

    M. V. Gashnikov

  2. IPSI RAS—Branch of the FSRC “Crystallography and Photonics,” Russian Academy of Sciences, 443001, Samara, Russia

    M. V. Gashnikov

Authors
  1. M. V. Gashnikov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. V. Gashnikov.

Ethics declarations

The authors declare that they have no conflicts of interest.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gashnikov, M.V. Multidimensional Signal Interpolation Based on Factorization and Dimension Reduction of Decision Rules. Opt. Mem. Neural Networks 28, 332–342 (2019). https://doi.org/10.3103/S1060992X1904009X

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S1060992X1904009X

Keywords:

Search

Navigation