Skip to main content
SpringerLink
Log in

Perturbations in Coriolis and Centrifugal Forces and N-R Basins of Convergence of Photogravitational Magnetic-Binary Problem with Variable Mass

  • POSITIONAL AND THEORETICAL ASTRONOMY
  • Published:
Kinematics and Physics of Celestial Bodies Aims and scope Submit manuscript

Abstract

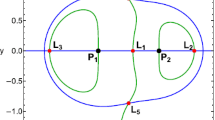
In this paper, we have investigated the effect of small perturbations in the Coriolis (ϕ) and centrifugal (ψ) forces in the Photogravitational magnetic binary problem including the effect of third body as variable mass. The objective of this work is to analyse the effect of ψ and other parameters (magnetic moments (λ) and radiation pressure (q)) on the existence and evolution of equilibrium points, basins of convergence (BoC), degree of unpredictability in BoC. In addition, to examine the effect of ϕ and ψ (in the presence of other parameters) on the stability of equilibrium points are also one of the aspect of this work. For different values of parameters, a total number of cases of non-collinear equilibrium points are 3, 5 and 7. The effect of various parameters on the evolution of equilibrium points are explained with the help of graphs. All non-collinear equilibrium points are found to be unstable for permissible range of parameters present in this model. The change in geometry of BoC’s is also shown and explained using graphs. The effect of ψ, q and λ on the degree of unpredictability in BoC’s is examined using the method of basin entropy. It is found that for the complete range of λ and q, the BoC’s are in fractal region. Also, for the values of ψ = 1.37, 1.38 and 1.40 to 1.44, the boundaries of BoC’s are in non-fractal region.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.

Similar content being viewed by others

REFERENCES

  1. R. Aggarwal, A. Mittal, M. S. Suraj, and V. Bisht, “The effect of small perturbations in the Coriolis and centrifugal forces on the existence of libration points in the restricted four-body problem with variable mass,” Astron. Nachr. 339, 492–512 (2018). https://doi.org/10.1002/asna.201813411

    Article  ADS  Google Scholar 

  2. K. B. Bhatnagar and P. P. Hallan, “Effect of perturbations in Coriolis and centrifugal forces on the stability of libration points in the restricted problem,” Celestial Mech. 18, 105–112 (1978). https://doi.org/10.1007/BF01228710

    Article  ADS  MathSciNet  MATH  Google Scholar 

  3. K. B. Bhatnagar and P. P. Hallan, “The effect of perturbations in Coriolis and centrifugal forces on the nonlinear stability of equilibrium points in the restricted problem of three bodies,” Celestial Mech. 30, 97–114 (1983). https://doi.org/10.1007/BF01231105

    Article  ADS  MathSciNet  MATH  Google Scholar 

  4. A. Daza, G. Bertrand, D. Guery-Odelin, A. Wagemakers, and M. A. F. Sanjuan, “Chaotic dynamics and fractal structures in experiments with cold atoms,” Phys. Rev. A 95, 013629 (2017). https://doi.org/10.1103/PhysRevA.95.013629

    Article  ADS  Google Scholar 

  5. A. Daza, A. Wagemakers, B. Georgeot, D. Guery-Odelin, and M. A. F. Sanjuan, “Basin entropy: A new tool to analyze uncertainty in dynamical systems,” Sci. Rep. 6, 31416 (2016). https://doi.org/10.1038/srep31416

    Article  ADS  Google Scholar 

  6. M. J. Idrisi, M. S. Ullah, and A. Sikkandhar, “Effect of perturbations in Coriolis and centrifugal forces on libration points in the restricted six-body problem,” J. Astronaut. Sci. 68, 4–25 (2021). https://doi.org/10.1007/s40295-021-00254-3

    Article  ADS  Google Scholar 

  7. J. H. Jeans, Astronomy and Cosmogony (Cambridge Univ. Press, Cambridge, 1928). https://doi.org/10.1017/S0016756800107861

    Book  MATH  Google Scholar 

  8. V. Kumar, M. Arif, and M. S. Ullah, “Capricious basins of attraction in photogravitational magnetic binary problem,” New Astron. 83, 101475 (2021). https://doi.org/10.1016/j.newast.2020.101475

    Article  Google Scholar 

  9. V. Kumar, M. J. Idrisi, and M. S. Ullah, “Unpredictable basin boundaries in restricted six-body problem with square configuration,” New Astron. 82, 101451 (2021). https://doi.org/10.1016/j.newast.2020.101451

    Article  Google Scholar 

  10. V. Kumar and S. K. Marig, “Effect of variable mass on N–R basins of convergence in photogravitational magnetic binary problem,” Astron. Rep. 67, 194–208 (2023). https://doi.org/10.1134/S1063772923020105

    Article  ADS  Google Scholar 

  11. V. Kumar, P. Sharma, R. Aggarwal, S. Yadav, and B. Kaur, “The unpredictability of the basins of attraction in photogravitational Chermnykh’s problem,” Astrophys. Space Sci. 365, 1–19 (2020). https://doi.org/10.1007/s10509-020-03815-4

    Article  MathSciNet  Google Scholar 

  12. I. V. Meshcherskii, Studies on the Mechanics of Bodies of Variable Mass (Gostekhizdat, Moscow, 1949) [in Russian].

    MATH  Google Scholar 

  13. A. K. Shrivastava and B. Ishwar, “Equations of motion of the restricted problem of three bodies with variable mass,” Celestial Mech. 30, 323–328 (1983). https://doi.org/10.1007/BF01232197

    Article  ADS  MathSciNet  MATH  Google Scholar 

  14. J. Singh and B. Ishwar, “Effect of perturbations on the location of equilibrium points in the restricted problem of three bodies with variable mass,” Celestial Mech. 32, 297–305 (1984). https://doi.org/10.1007/BF01229086

    Article  ADS  MathSciNet  MATH  Google Scholar 

  15. J. Singh and B. Ishwar, “Effect of perturbations on the stability of triangular points. In the restricted problem of three bodies with variable mass,” Celestial Mech. 35, 201–207 (1985). https://doi.org/10.1007/BF01227652

    Article  ADS  MATH  Google Scholar 

  16. J. Singh and A. E. Vincent, “Effect of perturbations in the Coriolis and centrifugal forces on the stability of equilibrium points in the restricted four-body problem,” Few-Body Syst. 56, 713–723 (2015). https://doi.org/10.1007/s00601-015-1019-3

    Article  ADS  Google Scholar 

  17. M. S. Suraj, R. Aggarwal, and M. Arora, “On the restricted four-body problem with the effect of small perturbations in the Coriolis and centrifugal forces,” Astrophys. Space Sci. 362, 1–11 (2017). https://doi.org/10.1007/s10509-017-3123-y

    Article  MathSciNet  Google Scholar 

  18. M. S. Suraj, R. Aggarwal, M. C. Asique, and A. Mittal, “On the basins of convergence in the magnetic-binary problem with angular velocity,” Comput. Math. Meth. 3, e1161 (2021). https://doi.org/10.1002/cmm4.1161

    Article  MathSciNet  Google Scholar 

  19. M. S. Suraj, P. Sachan, A. Mittal, and R. Aggarwal, “The effect of small perturbations in the Coriolis and centrifugal forces in the axisymmetric restricted five-body problem,” Astrophys. Space Sci. 364, 44 (2019). https://doi.org/10.1007/s10509-019-3528-x

    Article  MathSciNet  Google Scholar 

  20. V. Szebehely, “Stability of the points of equilibrium in the restricted problem,” Astron. J. 72, 7–41 (1967). https://doi.org/10.1016/B978-0-12-395732-0.50007-6

    Article  ADS  Google Scholar 

  21. A. Wintner, The Analytical Foundations of Celestial Mechanics (Princeton Univ. Press, Princeton, 1941). https://doi.org/10.1038/149534a0

    Book  MATH  Google Scholar 

  22. Mathematica, Version 12.0 (Wolfram Research, Champaign, Ill., 2019).

  23. E. E. Zotos, “Determining the Newton–Raphson basins of attraction in the electromagnetic Copenhagen problem,” Int. J. Non-Linear Mech. 90, 111–123 (2017). https://doi.org/10.1016/j.ijnonlinmec.2017.01.009

    Article  ADS  Google Scholar 

  24. E. E. Zotos, E. I. Abouelmagd, and Abd E1 N. S. Motelp, “Introducing a new version of the restricted three-body problem with a continuation fraction potential,” New Astron. 81, 101444 (2020). https://doi.org/10.1016/j.newast.2020.101444

    Article  Google Scholar 

  25. E. E. Zotos, W. Chen, E. I. Abouelmagd, and H. Han, “Basins of convergence of equilibrium points in the restricted three-body problem with modified gravitational potential,” Chaos, Solitons Fractals 134, 109704 (2020). https://doi.org/10.1016/j.chaos.2020.109704

    Article  MathSciNet  MATH  Google Scholar 

Download references

ACKNOWLEDGMENTS

Authors owe sincere thanks to Center for Fundamental Research in Space dynamics and Celestial mechanics (CFRSC), New Delhi, India for providing research facilities to complete this paper.

Funding

This work was supported by ongoing institutional funding. No additional grants to carry out or direct thisparticular research were obtained.

Author information

Authors and Affiliations

  1. Department of Mathematics, Zakir Husain Delhi College, University of Delhi, 110001, Delhi, India

    Vinay Kumar

  2. Department of Mathematics, Ramjas College, University of Delhi, 110007, Delhi, India

    Sawan Kumar Marig

Authors
  1. Vinay Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sawan Kumar Marig
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sawan Kumar Marig.

Ethics declarations

The authors declare that they have no conflicts of interest.

Additional information

Publisher’s Note.

Allerton Press remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vinay Kumar, Sawan Kumar Marig Perturbations in Coriolis and Centrifugal Forces and N-R Basins of Convergence of Photogravitational Magnetic-Binary Problem with Variable Mass. Kinemat. Phys. Celest. Bodies 39, 325–341 (2023). https://doi.org/10.3103/S0884591323060065

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S0884591323060065

Keywords:

Search

Navigation