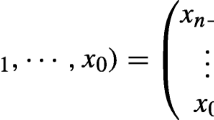Skip to main content
SpringerLink
Log in

Extending Nyberg construction on Galois fields of odd characteristic

  • Published:
Radioelectronics and Communications Systems Aims and scope Submit manuscript

Abstract

As is known, the Nyberg design S-boxes possess the cryptographic properties valuable for practical application. Up to date this construction has been considered only for fields of characteristic 2. This paper presents an extension of the Nyberg construction to the fields of odd characteristic. The notion of nonlinearity distance of p-function is introduced, and the affine ternary code is built. The Nyberg design S-boxes with fields characteristic p = 3 for all lengths N ≤ 243 are built. The nonlinearity distances are calculated, and it is shown that with an increase of S-box length, these distances increase essentially faster as compared to the fields of characteristic p = 2.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. O. N. Zhdanov, The Technique of Core Information Selection for Block Encryption Algorithm [in Russian] (INFRA-M, Moscow, 2013).

    Google Scholar 

  2. A. V. Sokolov, New Methods for Synthesis of Nonlinear Transformations of Modern Ciphers [in Russian] (Lap Lambert Academic Publishing, Germany, 2015).

    Google Scholar 

  3. Standard GOST 28147-89. Data Processing Systems. Cryptographic Security. Cryptographic Transformation Algorithm (IPK Izdatel’stvo standartov, Moscow, 1996).

    Google Scholar 

  4. S. Mister, C. Adams, “Practical S-box design,” Proc. of Workshop in Selected Areas of Cryptography, SAC’96, (1996), pp. 61–76. URI: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.40.7715&rep=rep1&type=pdf.

    Google Scholar 

  5. T. E. Medvedeva, “The S-boxes cryptography robustness assessment of GOST 28147-89 algorithm,” Reshetnevskie Chteniya, 666 (2012). URI: http://disk.sibsau.ru/website/reshetnevsite/materials/2012_2.pdf.

    Google Scholar 

  6. T. A. Chalkin, “Development of the parameter selection technique for the algorithm of constructing S-boxes of the block cipher standard GOST 28147-89,” Proc. of III Int. Conf. on Pressing Security Problems of Information Technologies, 2009, Sib. Gos. Aerokosmich. Un-t, Russia. Krasnoyarsk (2009).

    Google Scholar 

  7. FIPS 197. Advanced encryption standard, 2001. URI: http://csrc.nist.gov/publications/.

    Google Scholar 

  8. K. Nyberg, “Differentially uniform mappings for cryptography,” Advances in cryptology. Proc. of EUROCRYPT’93, Lecture Notes in Computer Science 765, 55 (1994). DOI: 10.1007/3-540-482 85-7_6.

    Article  MathSciNet  MATH  Google Scholar 

  9. M. I. Mazurkov and A. V. Sokolov, “Nonlinear transformations based on complete classes of isomorphic and automorphic representations of field GF(256),” Radioelectron. Commun. Syst. 56, No. 11, 513 (2013). DOI: 10.3103/S0735272713110022.

    Article  Google Scholar 

  10. M. I. Mazurkov and A. V. Sokolov, “Cryptographic properties of nonlinear transform of Rijndael cipher based on complete classes of irreducible polynomials,” Odes’kyi Politechnichnyi Universystet. Pratsi, No. 2, 183 (2012). URI: http://pratsi.opu.ua/articles/show/864.

    Google Scholar 

  11. A. S. Ambrosimov, “Properties of bent functions of q-valued logic over finite fields,” Discrete Math. Appl. 4, No. 4, 341 (1994). DOI: 10.1515/dma.1994.4.4.341.

    Article  MathSciNet  MATH  Google Scholar 

  12. R. Lidl and H. Niederreiter, Finite Fields, 2nd ed. CUP, 1994.

    MATH  Google Scholar 

  13. Y.-S. Kim, J.-W. Jang, J.-S. No, T. Helleseth, “On p-ary bent functions defined on finite fields,” Mathematical Properties of Sequences and Other Combinatorial Structures. The Springer International Series in Engineering and Computer Science, vol. 726 (Springer, Boston, MA, 2002), pp. 65–76. DOI: 10.1007/978-1-4615-0304-0_8.

    Google Scholar 

  14. O. N. Zhdanov, A. V. Sokolov, “Block symmetric cryptographic algorithm based on principles of variable block length and many-valued logic,” Far East J. Electronics Commun. 16, No. 3, 573 (2016). DOI: 10.17654/EC016030573.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Siberian State Aerospace University, Krasnoyarsk, Russia

    O. N. Zhdanov

  2. Odessa National Polytechnic University, Odessa, Ukraine

    A. V. Sokolov

Authors
  1. O. N. Zhdanov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. V. Sokolov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. V. Sokolov.

Additional information

Original Russian Text © O.N. Zhdanov, A.V. Sokolov, 2017, published in Izvestiya Vysshikh Uchebnykh Zavedenii, Radioelektronika, 2017, Vol. 60, No. 12, pp. 696–703.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhdanov, O.N., Sokolov, A.V. Extending Nyberg construction on Galois fields of odd characteristic. Radioelectron.Commun.Syst. 60, 538–544 (2017). https://doi.org/10.3103/S0735272717120032

Download citation

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S0735272717120032

Search

Navigation