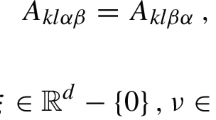Abstract
We construct a two-dimensional linear homogeneous differential system with piecewise continuous bounded coefficients whose set of all wanderability indicator values at various solutions consists of zero and a previously given finite set of positive numbers, and all those values are essential.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
I. N. Sergeev, “Determining the Wandering Characteristics of Solutions of a Linear System,” Diff. Uravn. 46 (6), 902 (2010).
I. N. Sergeev, “Oscillation and Wandering Characteristics of Solutions of a Linear Differential System,” Izvestiya Rus. Akad. Nauk, Ser. Matem. 76 (1), 149 (2012), [Izvestiya: Math. 76 (1), 139 (2012)].
E. M. Shishlyannikov, “The Example of a Differential System with Continual Spectrum of Wandering Exponent,” Vestn. Mosk. Univ., Matem. Mekhan., No. 1, 64 (2017).
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © E.M. Shishlyannikov, 2017, published in Vestnik Moskovskogo Universiteta, Matematika. Mekhanika, 2017, Vol. 72, No. 5, pp. 14–21.
About this article
Cite this article
Shishlyannikov, E.M. Two-dimensional differential systems with arbitrary finite spectra of wandering exponent. Moscow Univ. Math. Bull. 72, 192–198 (2017). https://doi.org/10.3103/S0027132217050023
Received:
Published:
Issue Date:
DOI: https://doi.org/10.3103/S0027132217050023