Skip to main content
SpringerLink
Log in

Optimal use of components of a dyadic wavelet representation

  • Published:
Moscow University Mathematics Bulletin Aims and scope

Abstract

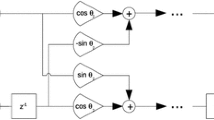
In practice, one may encounter linear transforms whose result is important for a certain set of vector components only. In particular this relates to vector components restored from its dyadic wavelet representation. In this paper we study optimization of the index set of the dyadic wavelet representation which can be used to restore required original vector components.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. S. Mallat, A Wavelet Tour of Signal Processing (Academic Press, 1999; Mir, Moscow, 2005).

  2. A. V. Mikhalev and A. V. Shokurov, “Optimal Use of Wavelet Components,” Uspekhi Matem. Nauk 62(4), 171 (2007) [Russ. Math. Surveys 62 (4), 816 (2007)].

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Moscow State University, Faculty of Mechanics and Mathematics, Leninskie Gory, Moscow, 119991, Russia

    A. V. Shokurov

Authors
  1. A. V. Shokurov
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Original Russian Text © A.V. Shokurov, 2009, published in Vestnik Moskovskogo Universiteta, Matematika. Mekhanika, 2009, Vol. 64, No. 5, pp. 3–6.

About this article

Cite this article

Shokurov, A.V. Optimal use of components of a dyadic wavelet representation. Moscow Univ. Math. Bull. 64, 179–182 (2009). https://doi.org/10.3103/S0027132209050015

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S0027132209050015

Keywords

Search

Navigation