Skip to main content
SpringerLink
Log in

Scattering of Plane SH Waves Around a Lined Tunnel in the Covering Layer of Composite Strata

  • Published:
Mechanics of Solids Aims and scope Submit manuscript

Abstract

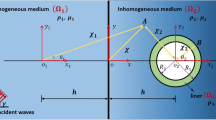
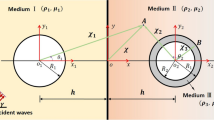
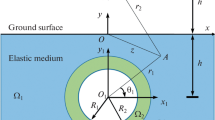
This paper presents analytical solutions to the dynamic response of a lined tunnel in the covering soil layer of composite strata under the incident SH waves by using the complex function method and conformal mapping technique. It is more important to analyze the scattering of elastic waves in the composite stratum because of the existence of boundaries between the soil layers. By applying the conformal mapping technique instead of the large-arc assumption method, the straight boundaries of the covering layer and the circular boundaries of a lined tunnel are transformed into several circles on other complex planes. An infinite linear equation system is established and is solved based on the stress and displacement boundary conditions at the boundaries of the composite stratum and the tunnel lining. The impacts on the dynamic response of a lined tunnel in several types of composite strata, “soft-over-hard” and “hard-over-soft” with “flexible lining” and “rigid lining” are analyzed through the calculation examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.
Fig. 9.
Fig. 10.

Similar content being viewed by others

REFERENCES

  1. Y. H. Pao and C. C. Mow, “The diffraction of elastic waves and dynamic stress concentration,” J. Appl. Mech. 40 (4), 872 (1973). https://doi.org/10.1115/1.3423178

    Article  ADS  Google Scholar 

  2. M. D. Trifunac, “Scattering of plane SH waves by a semi-cylindrical canyon,” Earthq. Eng. Struct. Dyn. 1, 267–281 (1973). https://doi.org/10.1002/eqe.4290010307

    Article  Google Scholar 

  3. M. D. Trifunac and V. W. Lee, “Response of tunnels to incident SH waves,” J. Eng. Mech. Div. 105 (4), 643–659 (1979). https://doi.org/10.1061/jmcea3.0002511

    Article  Google Scholar 

  4. J. Liang, L. Yan, and V. W. Lee, “Scattering of plane P waves by circular-arc layered alluvial valleys: An analytical solution,” Acta Seismol. Sinica 14 (2), 176–195 (2001).

    Article  ADS  Google Scholar 

  5. J. Liang, L. Yan, and V. W. Lee, “Effects of a covering layer in a circular-arc canyon on incident plane SV waves,” Acta Seismol. Sinica 14 (2), 660–675 (2001).

    Article  ADS  Google Scholar 

  6. J. Yang and H. Qi, “The scattering of steady-state SH waves in a bi-material half space with multiple cylindrical elastic inclusions,” Wave Random Complex 29 (1), 162–177 (2019). https://doi.org/10.1080/17455030.2017.1418541

    Article  ADS  MATH  Google Scholar 

  7. W. Scheidl and F. Zieglar, “Interaction of a pulsed Rayleigh surface wave and a rigid cylindrical inclusion,” in Modern Problems in Elastic Wave Propagation (JohnWiley & Sons, New York, 1978), Vol. 99, pp. 145–169.

    Google Scholar 

  8. H. P. Brandow and V. Lee, “Scattering and diffraction of plane P-waves in a 2-D elastic half-space II: Shallow arbitrary shaped canyon,” Earthq. Eng. Eng. Vib. 16, 459–485 (2017). https://doi.org/10.1007/s11803-017-0395-8

    Article  Google Scholar 

  9. D. Liu, B. Gai, and G. Tao, “Applications of the method of complex functions to dynamic stress concentrations,” Wave Motion 4, 293–304 (1982). https://doi.org/10.1016/0165-2125(82)90025-7

    Article  ADS  MathSciNet  MATH  Google Scholar 

  10. M. Dravinski and R. Sheikhhassani, “Scattering of a plane harmonic SH wave by a rough multilayered inclusion of arbitrary shape,” Wave Motion 50 (4), 836–851 (2013). https://doi.org/10.1016/j.wavemoti.2013.02.014

    Article  ADS  MathSciNet  MATH  Google Scholar 

  11. R. Sheikhhassani and M. Dravinski, “Scattering of a plane harmonic SH wave by multiple layered inclusions,” Wave Motion 51 (3), 517–532 (2014). https://doi.org/10.1016/j.wavemoti.2013.12.002

    Article  ADS  MathSciNet  MATH  Google Scholar 

  12. M. Dravinski and R. Sheikhhassani, “Dynamic stress concentration for multiple multilayered inclusions embedded in an elastic half-space subjected to SH-waves,” Wave Motion 62, 20–40 (2016). https://doi.org/10.1016/j.wavemoti.2015.11.002

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. S. Gupta and N. Bhengra, “Influence of magnetoelasticity on frequency equation of shear wave propagation in a multilayered magnetoelastic anisotropic monoclinic medium,” Appl. Math. Comput. 355, 366–384 (2019). https://doi.org/10.1016/j.amc.2019.03.006

    Article  MathSciNet  MATH  Google Scholar 

  14. W. Shyu, T. Teng, and C. Chou, “Anti-plane response caused by interactions between a dike and the surrounding soil,” Soil Dyn. Earthq. Eng. 92, 408–418 (2017). https://doi.org/10.1016/j.soildyn.2016.10.014

    Article  Google Scholar 

  15. W. Shyu, C. Chou, and C. Lu, “Anti-plane responses of acceleration by a shallow hill next to an alluvial valley,” Eng. Geol. 277, 105777 (2020). https://doi.org/10.1016/j.enggeo.2020.105777

  16. J. Liang, Z. Liu, L. Huang, and G. Yang, “The indirect boundary integral equation method for the broadband scattering of plane P, SV and Rayleigh waves by a hill topography,” Eng. Anal. Boundary Elem. 98, 184-202 (2019). https://doi.org/10.1016/j.enganabound.2018.09.018

    Article  MathSciNet  MATH  Google Scholar 

  17. Z. Ba, Y. Wang, J. Liang, and V. W. Lee, “Wave scattering of plane P, SV, and SH waves by a 3D alluvial basin in a multilayered half-space,” Bull. Seismolog. Soc. Am. 110 (2), 576–595 (2020). https://doi.org/10.1785/0120190090

    Article  Google Scholar 

  18. Z. Ba, E. Zhang, J. Liang, et al., “Two-dimensional scattering of plane waves by irregularities in a multilayered transversely isotropic saturated half-space,” Eng. Anal. Boundary Elem. 118, 169–187 (2020). https://doi.org/10.1016/j.enganabound.2020.06.006

    Article  MathSciNet  MATH  Google Scholar 

  19. H. Qi, Y. Zhang, F. Chu, and J. Guo, “Scattering of SH waves by a partially debonded cylindrical inclusion in the covering layer,” Math. Probl. Eng. 2020, 1–13 (2020). https://doi.org/10.1155/2020/2614574

    Article  MathSciNet  Google Scholar 

  20. H. Qi, Y. Zhang, J. Guo, and F. Chu, “Dynamic stress analysis of a circular-lined tunnel in composite strata-SH wave incidence,” Adv. Civil Eng. 2020, 1–13 (2020). https://doi.org/10.1155/2020/8827737

    Article  Google Scholar 

  21. M. Xiang, H. Qi, and J. Guo, “The anti-plane scattering of sh waves by the non-circular cavity in an infinite strip,” J. Earthquake Eng. 26 (6), 3228–3245 (2022). https://doi.org/10.1080/13632469.2020.1793843

    Article  Google Scholar 

Download references

ACKNOWLEDGMENTS

This work was conducted with jointly supports from the National Natural Science Foundation of China (Grant nos. 52004052;51808100;U1602232), the Key Research and Development Program of Science and Technology in Liaoning Province, China (2019JH2/10100035).

Author information

Authors and Affiliations

  1. School of Resource and Civil Engineering, Northeastern University, 110819, Shenyang, China

    Song-Chol Ri & Shuhong Wang

  2. Department of Mechanical Science, Kim Chaek University of Technology, 950003, Pyongyang, Democratic People’s Republic of Korea

    Song-Chol Ri

  3. Key Laboratory of Ministry of Education on Safe Mining of Deep Metal Mines, Northeastern University, 110819, Shenyang, China

    Shuhong Wang

  4. Faculty of Energy Science, Kim Il Sung University, 950003, Pyongyang, Democratic People’s Republic of Korea

    Hak-Son Jin

Authors
  1. Song-Chol Ri
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shuhong Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hak-Son Jin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Song-Chol Ri or Shuhong Wang.

Ethics declarations

The authors declare that they have no conflicts of interest.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ri, SC., Wang, S. & Jin, HS. Scattering of Plane SH Waves Around a Lined Tunnel in the Covering Layer of Composite Strata. Mech. Solids 58, 1806–1820 (2023). https://doi.org/10.3103/S002565442360112X

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S002565442360112X

Keywords:

Search

Navigation