Abstract
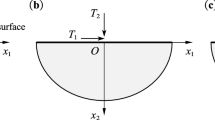
The axisymmetric contact problem of interaction between a two-layer foundation and a rigid annular punch is considered under the assumption that the surface nonuniformity of the upper layer and the shape of the punch base are described by rapidly varying functions. The integral equation of the problem containing two rapidly varying functions is derived, and two versions of the problem are considered. Their solutions were first constructed by the generalized projection method. As an illustration, the model problem is analyzed numerically to demonstrate the high efficiency of the method.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. M. Alexandrov and S. M. Mkhitaryan, Contact Problems for Bodies with Thin Covers and Interlayers (Nauka, Moscow, 1983) [in Russian].
A. V. Manzhirov, “Axisymmetric Contact Problems for Non-Uniformly Aging Layered Viscoelastic Foundations,” Prikl. Mat. Mekh. 47 (4), 684–693 (1983) [J. Appl. Math. Mech. (Engl. Transl.) 47 (4), 558–566 (1983)].
V. M. Alexandrov, “Contact Problems on Soft and Rigid Coatings of an Elastic Half-Plane,” Izv. Ross. Akad. Nauk. Mekh. Tverd. Tela, No. 1, 42–50 (2010) [Mech. Solids (Engl. Transl.) 45 (1), 34–40 (2010)].
N. F. Morozov and P. E. Tovstik, “BucklingModes of a CompressedPlate on an Elastic Substrate,” Izv. Ross. Akad. Nauk. Mekh. Tverd. Tela, No. 6, 30–36 (2012) [Mech. Solids (Engl. Transl.) 47 (6), 622–627 (2012)].
A. V. Manzhirov, “On a Method of Solving Two-Dimensional Integral Equations of Axisymmetric Contact Problems for Bodies with Complex Rheology,” Prikl. Mat. Mekh. 49 (6), 1019–1025 (1985) [J. Appl.Math. Mech. (Engl. Transl.) 49 (6), 777–782 (1985)].
K. E. Kazakov, “Contact Problems for Coated Bodies,” Vestnik SamGU. Estestvennonauch. Ser., No. 4, 176–196 (2007).
K. E. Kazakov and A. V. Manzhirov, “Conformal Contact between Layered Foundations and Punches,” Izv. Ross. Akad. Nauk.Mekh. Tverd. Tela, No. 3, 227–240 (2008) [Mech. Solids (Engl. Transl.) 43 (3), 512–524 (2008)].
A. V. Manzhirov and K. E. Kazakov, “Contact Problem for a Foundation with a Rough Coating,” Lect. Notes Eng. Comput. Sci. 2224, 877–882 (2016).
A. V. Manzhirov, “A Mixed Integral Equation of Mechanics and a Generalized Projection Method of Its Solution,” Dokl. Ross. Akad. Nauk 470 (4), 401–405 (2016) [Dokl. Phys. (Engl. Transl.) 61 (10), 489–493 (2016)].
E. Goursat, Cours d’Analyse Mathéematique, Tome III. Intéegrales Infiniment Voisines; Équations aux Dérivées Partielles du Second Ordre; Équations Intégrales; Calcul des Variations (Gauthier–Villars, Paris, 1927; GTTI, Moscow–Leningrad, 1934).
S. G. Mikhlin, N. F. Morozov, and M. V. Paukshto, Integral Equations in Theory of Elasticity (Izdat. St. Peterburg Univ., St. Peterburg, 1994) [in Russian].
I. I. Vorovich, V. M. Alexandrov, and V. A. Babeshko, Nonclassical Mixed Problems of Elasticity (Nauka, Moscow, 1974) [in Russian].
V. S. Vladimirov, Equations of Mathematical Physics (Nauka, Moscow, 1981) [in Russian].
G. Szegö, Orthogonal Polynomials (Amer. Math. Soc, Providence, 1959; Fizmatgiz, Moscow, 1962).
A. N. Kolmogorov and S. V. Fomin, Elements of the Theory of Functions and Functional Analysis (Nauka, Moscow, 1976; Dover Publications, New York, 1999).
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © K.E. Kazakov, A.V. Manzhirov, 2017, published in Izvestiya Akademii Nauk, Mekhanika Tverdogo Tela, 2017, No. 4, pp. 112–120.
About this article
Cite this article
Kazakov, K.E., Manzhirov, A.V. Axisymmetric contact between an annular rough punch and a surface nonuniform foundation. Mech. Solids 52, 444–451 (2017). https://doi.org/10.3103/S0025654417040112
Received:
Published:
Issue Date:
DOI: https://doi.org/10.3103/S0025654417040112