Skip to main content
SpringerLink
Log in

Dynamics of a homogeneous ball on a horizontal plane with sliding, spinning, and rolling friction taken into account

  • Published:
Mechanics of Solids Aims and scope Submit manuscript

Abstract

We analyze the dynamics of a homogeneous ball on a horizontal plane with friction of all kinds, namely, sliding, spinning, and rolling friction, taken into account. The qualitative-analytic study of the ball dynamics is supplemented with numerical experiments.

The problem on the motion of a homogeneous ball on a horizontal plane with friction was apparently first studied in 1758 by I. Euler (Leonard Euler’s son) with sliding friction taken into account in the framework of the Coulomb model. I. Euler showed that the ball sliding ceases in finite time, after which the ball uniformly rolls along a fixed straight line and uniformly spins about the vertical. This result has long become classical and is described in many textbooks on theoretical mechanics.

In 1998, V. F. Zhuravlev considered the problem of motion of a homogeneous ball on a horizontal plane with sliding and spinning friction taken into account in the framework of the Contensou-Zhuravlev model [1, 2] and showed that the ball sliding and spinning cease simultaneously, after which the ball uniformly rolls along a fixed straight line. The Contensou-Zhuravlev theory was further developed in [3–7].

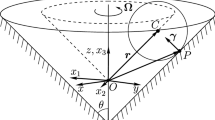
In the present paper, we consider themotion of a homogeneous ball on a horizontal plane with friction of all kinds taken into account in the framework of the model proposed in [8]. We show that, in one and the same time, both the sliding velocity and the angular velocity of the ball become zero. Our studies are based on the results obtained in [2], the properties of the friction model proposed in [8], and the method for qualitative analysis of dynamics of dissipative systems [9, 10]. The qualitative-analytic study is supplemented with numerical experiments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. P. Contensou, “Couplage Entre Frottenment de Glissement et Frottenment de PivotementDans la Théorie de la Toupie,” in Kreiselprobleme Gyrodynamics (IUTAM Symp.Celerina, Berlin etc., Springer; Mir, Moscow, 1967), pp. 201–216 (60–77).

    Google Scholar 

  2. V. Ph. Zhuravlev, “The Model of Dry Friction in the Problem of the Rolling of Rigid Bodies,” Prikl. Mat. Mekh. 62(5), 762–767 (1998) [J. Appl. Math. Mech. (Engl. Transl.) 62 (5), 705–710 (1998)].

    MathSciNet  Google Scholar 

  3. A. A. Kireenkov, “A Method for the Calculation of the Force and Torque of Friction in a Combined Model of Dry Friction for Circular Contact Areas,” Izv. Akad. Nauk. Mekh. Tverd. Tela, No. 3, 51–56 (2003) [Mech. Solids (Engl. Transl.) 38 (3), 39–43 (2003)].

  4. V. Ph. Zhuravlev, “Friction Laws in the Case of Combination of Slip and Spin,” Izv. Akad. Nauk. Mekh. Tverd. Tela, No. 4, 81–88 (2003) [Mech. Solids (Engl. Transl.) 38 (4), 52–58 (2003)].

  5. V. Ph. Zhuravlev, “Dynamics of a Heavy Homogeneous Ball on a Rough Plane,” Izv. Ross. Akad. Nauk, Mekh. Tverd. Tela, No. 6, 3–9 (2006) [Mech. Solids (Engl. Transl.) 41 (6), 1–5 (2006)].

  6. A. A. Kireenkov, “Coupled Models of Sliding and Rolling Friction,” Dokl. Ross. Akad. Nauk 419(6), 759–762 (2008) [Dokl. Phys. (Engl. Transl.) 53 (4), 233–236 (2008)].

    Google Scholar 

  7. A. A. Kireenkov, “Combined Model of Sliding and Rolling Friction in Dynamics of Bodies on a Rough Plane,” Izv. Akad. Nauk. Mekh. Tverd. Tela, No. 3, 116–131 (2008) [Mech. Solids (Engl. Transl.) 43 (3), 412–425 (2008)].

  8. A. V. Karapetyan, “A Two-Parameter Friction Model,” Prikl. Mat. Mekh. 73(4), 515–519 (2009) [J. Appl. Math. Mech. (Engl. Transl.) 73 (4), 367–370 (2009)].

    MathSciNet  Google Scholar 

  9. A. V. Karapetyan, “Global Qualitative Analysis of Tippe Top Dynamics,” Izv. Akad. Nauk. Mekh. Tverd. Tela, No. 3, 33–41 (2008) [Mech. Solids (Engl. Transl.) 43 (3), 342–348 (2008)].

  10. A. V. Karapetyan, “Qualitative Analysis od Dynamics of Dissipative Systems with Symmetry on the Basis of the Method of Generalized Smale Diagrams,” in Contemporary Problems in Mathematics and Mechanics, Vol. 2: Mechanics, No. 2 (Izd-vo MGU, Moscow, 2009), pp. 192–200 [in Russian].

    Google Scholar 

  11. M. V. Ishkhanyan, “Dynamics of a Homogeneous Ball on the Surface with Friction,” in Proc. Conference—Competition of Young Scientists of Institute of Mechanics, MSU (Izd-vo MGU, Moscow, 2009), pp. 99–105 [in Russian].

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Lomonosov Moscow State University, GSP-2, Leninskie Gory, Moscow, 119992, Russia

    M. V. Ishkhanyan & A. V. Karapetyan

Authors
  1. M. V. Ishkhanyan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. V. Karapetyan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. V. Ishkhanyan.

Additional information

Original Russian Text © M.V. Ishkhanyan, A.V. Karapetyan, 2010, published in Izvestiya Akademii Nauk. Mekhanika Tverdogo Tela, 2010, No. 2, pp. 3–14.

About this article

Cite this article

Ishkhanyan, M.V., Karapetyan, A.V. Dynamics of a homogeneous ball on a horizontal plane with sliding, spinning, and rolling friction taken into account. Mech. Solids 45, 155–165 (2010). https://doi.org/10.3103/S0025654410020019

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S0025654410020019

Key words

Search

Navigation