Introduction

Clay minerals are among the most abundant materials in the world. The use of natural clay minerals in mostly high-tech application areas is hampered by the fact that they typically occur together with other mineral contaminants, and also exhibit inhomogeneities and defects in the structure.1–3 Thus, for using these materials in high-tech applications, defect-free pure clay without contamination is needed in the first step. One very familiar example of a clay mineral-based dielectric material is mica,4,5 one of the longest known dielectric materials,5 which exhibits a wide bandgap of 7.85 eV. Exfoliated mica is very useful as a highly insulating nanosheet for deposition of conductive single nanosheets, such as graphene.6–8 However, delamination of mica nanosheets is not driven by thermodynamics, and can only be obtained by liquid-phase exfoliation, and in the only small amounts when applying high-energy ultrasonication.9 When reducing the number of layers in mica, the bandgap energy (E\(_g\)) increases due to quantum size effects, as is typical for such materials, for instance hBN, dichalcogenides, black phosphorus, transition-metal oxides such as \(\hbox {MoO}_2\), \(\hbox {MoO}_3\), perovskites, topological insulators, and others.10 However, despite the confirmed insulating property of bulk mica and few-layer mica,4,5,8,11 there is one report suggesting that exfoliation of K-mica reduces E\(_g\) from 7.85 to 2.5 eV with reduction of the number of nanosheets.12 As tunneling might occur across thin nanosheets,13 we propose that the reported counter intuitive result12 likely could be due to the tunneling effects rather than the narrowing of the bandgap.13 Apart from this one exception, all other published data show an insulating character of single mica nanosheets.5,8,11 To avoid parasitic effects from impurities or defects in the experimental studies and interpretations, and further on in applications, we study here the highly crystalline and pure synthetic fluorohectorite clay (Fh), which is a close sibling of natural clay minerals and mica.14,15

The band structure of Fh nanosheets has not yet been examined. One of the most powerful techniques for E\(_g\) determination, electron energy-loss spectroscopy (EELS)16,17 is utilized. The high energy resolution offered by EELS combined with the high spatial resolution of transmission electron microscopy (TEM) allows direct determination of the bandgap, without any manipulations. In EELS, fast electrons from a beam interact with the sample, causing a number of various sample excitations, including excitation of valence electrons to the conduction band. Apart from bandgap excitation, the low loss region in EELS can possibly also include bulk and surface plasmons, excitation from interband transitions or light guided modes, and Cerenkov losses.18,19 However, the low refractive index (app. 1.49–1.521,20) and limited thickness of the synthetic Fh nanosheets combined with relatively low electron-beam energies used (80-kV electrons) totally suppress Cerenkov loss and losses from guided modes. In our samples, an increase of intensity in measured spectra, for example, dependence of the intensity on energy, I(E), thus ideally corresponds directly to the bandgap of the examined material if surface plasmons are not present.

Here, we report both a measured and DFT calculated E\(_g\) for the high-aspect ratio single Fh nanosheets proving it to be a wide-bandgap insulator.

Results and discussion

Figure 1
figure 1

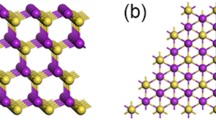
Unit-cell structure of non-hydrated Fh (without interlayer cations). In the pristine crystalline sample, nanosheets of 0.95-nm thickness are kept together by interlayer cations (Na+). At ambient humidity, Na+ is always hydrated.21 The Fh nanosheet consists of three sheets—one octahedral (orange octahedra) and two tetrahedral (blue tetrahedra) sheets, with the octahedral sheet sandwiched between the two tetrahedral sheets. The tetrahedra consist of \(\hbox {SiO}_2\) and octahedra of \(\hbox {Mg}_{2.5}\) \(\hbox {Li}_{0.5}\) \(\hbox {O}_4\) \(\hbox {F}_2\). Lattice parameters are a = 5.240 Å, b = 9.094 Å, c = 9.40, 12.371, and 13.60 Å, for the 0, 1, and 2 water layer hydrated clay, respectively.21

Full size image

Synthetic Fh shown in Figure 1 is a 2:1 phyllosilicate, which typically has nominal chemical formula per half-unit-cell \(\hbox {Na}_{0.5}\)-[\(\hbox {Mg}_{(2.5)}\) \(\hbox {Li}_{0.5}\)]\(\hbox {Si}_4\) \(\hbox {O}_{10}\) \(\hbox {F}_2.\)14,15 Fh from a synthesis consists of the stacks of these 0.95-nm thin, negatively charged single nanosheets22,23 kept together by charge compensating cations in the interlayer. The individual crystalline nanosheet is a “sandwich of sub-sheets” comprising three types of atomic sheets—two tetrahedral sheets of the \(\hbox {SiO}_2\) sandwiching one octahedral sheet, including metal elements inside (Figure 1). In Fh, the metallic sites are fully occupied by Mg and may be dopped by Li, for instance.15

Fh stacks have high affinity for water intercalation in the interlayers.24,25 Also, other types of molecules that are either positively charged, dipolar, or quadrupolar can be intercalated into the interlayers, depending on detailed interactions with the interlayer charges and species.26,27 Examples are green house gases28–32 (\(\hbox {CO}_2\), \(\hbox {CH}_4\)) or pharmaceutics.33,34

Fh crystallizes in a monoclinic crystal structure with the space group C2/m and exhibits three different hydration states (non-hydrated, 1, and 2 water layer hydrated). Lattice parameters are a = 5.240 Å, b = 9.094 Å, and c = 9.40, 12.371, and 13.60 Å for the 0, 1, and 2 water layer hydrated clay, respectively. After immersion into liquid water, Fh exhibits complete delamination by thermodynamically driven repulsive osmotic swelling into separate single nanosheets that can form a nematic structure with parallel alignment of suspended nanosheets.14,20,23

Fh can be delaminated by thermodynamically driven repulsive osmotic swelling into high-aspect ratio single nanosheets, as shown in the AFM image (Figure 2). Delaminated nanosheets appear to have a thickness of about 1.2 nm. Nominal XRD thickness of single nanosheets is 0.95 nm, and the larger thickness obtained by the AFM is due to adsorbed water layer underneath the Fh single nanosheet.

Figure 2
figure 2

The atomic force microscopy topography (top) and phase (bottom) images. Scale bar on the upper image determines height of the objects, in the lower image phase shift. Atomic force microscopy thickness of the nanosheets is approximately 1.2 nm.

Full size image

TEM images showed multiple nanosheets deposited on the lacey carbon foil. Selected nanosheets were examined by EELS. Spectra from two different regions are shown in Figure 3. Different points of the Brillouin zone (BZ) were studied (Figure 4). EEL spectra from the BZ center (i.e., direct bandgap excitations are probed), half way to the 1st BZ boundary (probing indirect transitions), and at the edge of the 1st Brillouin zone were also acquired (Figure 4).

The various EELS spectra exhibit an increase of intensity at selected energies, that can be attributed to valence to conduction band excitations. The onset of the peak in the EELS spectrum corresponds to transitions from the top of the valence band to the bottom of the conduction band.35 The EELS intensity at energies above the bandgap shows however a complex profile that does not correspond to the typical parabolic shape of the free electron gas. This is attributed to contributions from plasmons and potentially other types of excitations that change the shape of intensity profile. Additionally, the captured spectra exhibit a small increase of the intensity bellow 7 eV. This so-called pre-absorption edge can be attributed to the formation of excitons near the minimum of the valence band, or the presence of defect states located in the bandgap.

Figure 3
figure 3

Electron energy-loss spectroscopy spectra of single (blue) and few-layer (black) nanosheets. Bandgap energies determined from individual spectra are marked in the image.

Full size image
Figure 4
figure 4

Electron energy-loss spectroscopy spectra of Fh nanosheets in the center, half way, and at the boundary of the 1st Brillouin zone (BZ). Determined values of the bandgap are listed in the figure. ZLP is the zero-loss peak.

Full size image
Figure 5
figure 5

Irradiation damage by the electron beam, with dose corresponding to 15 s. With increasing dose, exposure of Fh increases by 15 s for each dose. Electron energy-loss spectroscopy spectra correspond to consecutively increasing dose, starting from nondamaged nanosheets (red spectrum, dose 1) all the way to completely amorphized nanosheets (purple spectrum, dose 7). Time scale of radiation damage is in the range of 2 minutes.

Full size image

All spectra were background subtracted by removal of the tail of the zero-loss peak (ZLP) by deconvolution of the exponential decay function in the Gatan digital micrograph software. The position of the minimum of the conduction band, which is directly attributed to E\(_g\), was approximated by a linear fit for the signal above the peak onset,35 as demonstrated in Figure 3, because the real data are far from a common theoretical model that obeying a \(I(E)\approx E^{1/2}\) dependence for the direct and a \(I(E)\approx ~E{^3/2}\) dependence for the indirect bandgap. The determined value of E\(_g\) is thus expected to slightly underestimate the real bandgap width. Moreover, direct and indirect bandgaps cannot be differentiated. All measured individual nanosheets and regions within the same nanosheet exhibit a spread of the E\(_g\) in the range of 7.1–7.5 eV, which shows that a Fh nanosheet is a wide-bandgap insulator. When scanning over the 1st Brillouin zone of Fh, E\(_g\) value ranges of 7.0–8.2 eV were found (Figure 4). This experimentally determined value of E\(_g\) is not surprising if we compare it with the E\(_g\) of individual bulk oxides forming the Fh, namely insulating MgO, and \(\hbox {SiO}_2\), with the ab initio calculated bandgaps of 3.82–7.6 for MgO,36,37 and 5.67 eV35,38,39 for \(\hbox {SiO}_2\), respectively. Experimental bandgaps of \(\hbox {SiO}_2\) and MgO are 7.5–9.6 eV40,41 and 5–7.6,37,42,43 respectively. Considering these E\(_g\) values, we can conclude that a wide bandgap of Fh can arise both from the \(\hbox {SiO}_2\) tetrahedral sheets and the metal oxides in the sandwiched octahedra.

Moreover, Fh nanosheets are prone to radiation damage by the electron beam, as can be seen in Figure 5. With increasing duration of irradiation, a gradual amorphization by beam damage was observed. Dose 7 (purple) in Figure 5 corresponds to a completely amorphized region of the sample. With increasing dose, the band E\(_g\) shifts from 7.3 eV up to 7.9 eV, approaching the value of the E\(_g\) of the \(\hbox {SiO}_2\) and MgO.

The determined bandgap of Fh nanosheets is also close to the bulk value for mica4 (7.85 eV) suggesting that it may be a good replacement for mica in applications. With readily available nanosheets, it will moreover enable faster fabrication of 2D heterostructures. Taking advantage of self-assembly properties of single Fh nanosheets, this will allow for upscaling rapid fabrication of sandwiched nanolayered structures.

Figure 6
figure 6

Band structure and density of states of Fh, obtained with the standard density functional theory approach. Inset panel shows the symmetry points in the 1st Brillouin zone for the Pmmm space group. The Fermi energy (E\(_f\)) is fixed in the middle gap. PDOS, projected density of states.

Full size image

To support experimental results by DFT, we estimate the Fh energy gap by calculating the band structure along the directions passing through the symmetry points of the Pmmm space group in the 1st Brillouin zone (see Figure 6). The flat structure observed in both valence and conduction bands reveals the high effective mass and localized condition of the electrons in the system. Analysis of projected density of states (PDOS) further reveals that the highest valence bands are mainly due to the contributions of Si and O electronic states. The highest valence and lowest conduction bands are separated by an energy bandgap of 5.55 eV at the same k-vector (direct bandgap). It is already well established that such DFT calculations underestimate the energy bandgap because it is a ground state approach.44 For instance, in the case of hexagonal boron nitride (h-BN), the DFT approach returns a value in the range 4.6445,46−4.96 eV,46,46–48 whereas the experimental data are in the range of 5.9549−6.8 eV50 for the single h-BN sheet. Considering the differences observed in other insulators, the energy bandgap obtained for the Fh system is reasonable compared to the experimental result. Despite these differences, it is a reliable finding that the energy bandgap for the Fh is greater than the one observed in wide-gap h-BN.

Figure 7
figure 7

(a) Dependence of the bandgap energy for different charges of fluorohectorite nanosheets (charge per unit cell). (b) Bandgap energy dependence on the number of nanosheets.

Full size image

We also explored the possibility of modifying the energy gap through point defects. The gradual replacement of Mg atoms by Li creates a charge imbalance in the system51 and modifies the crystal symmetry. As a consequence, the energy bandgap increases as a function of the number of substitutional atoms, according to Figure 7a. Moreover, following standard observation of increase of the bandgap with decreasing number of nanosheets typical in 2D materials, DFT showed expected behavior also for our Fh (Figure 7b).

Methods

Synthetic Fh has been prepared as described in Reference 15. Single clay nanosheets were obtained by delamination in deionized water. The delamination was obtained by continuously shaking the 1 wt% suspension for two days. Atomic force microscope (AFM) images of the single nanosheet were obtained with a Dimension Icon (Bruker) SPM, nanoscope IV controller (Veeco–Bruker) in the tapping mode. RTESP-150 probes (with \(\hbox {f}_0\) =150 kHz, r < 5 nm, Bruker probes) were used, minimizing wear of the tips. To prepare samples for the AFM measurements, a very dilute (0.5 × 10\(^{-3}\) M) nematic suspension was drop cast on clean Si and Si@\(\hbox {SiO}_2\)(100 nm) substrates and dried overnight. Samples for EELS were prepared by drop casting the same nematic suspension on Cu TEM grids coated by “lacey carbon” films (TedPella). EELS was performed with a double Cs aberration-corrected cold FEG JEOL ARM200FC, operated at 80 kV. This instrument is equipped with a GIF Quantum ER. All EELS acquisitions were done with dual EELS and the low loss spectrum, containing the zero-loss peak (ZLP), was used to calibrate the energy scale of the bandgap spectrum. The energy resolution was measured to be 0.50 eV, based on the full width at half maximum of the ZLP. All EELS spectra were acquired in diffraction mode with a broad beam (to avoid electron-beam damage) and where a selected-area diffraction aperture (covering a circular region of 150 nm in diameter on the sample) was used to determine what part of the sample should contribute to the EELS spectrum. All acquisitions (15 s) were taken at regions without any carbon film. All spectra were background subtracted by the removal of the tail of the zero-loss peak (ZLP) by deconvolution of the exponential decay function in the Gatan digital micrograph software. To support experimental results, we performed first-principles calculations within the DFT approach 52,53 to evaluate the E\(_g\) of the freestanding Fh nanosheets. To account for the dispersion of van der Waals interactions, we considered the state-of-the-art density functional developed by Berland and Hyldgaard54 as implemented in the Siesta package.55 The localized double-zeta polarized basis set with converged 400 Ry Mesh cutoff was adopted. The reciprocal space was represented by a grid of 16 × 16 × 1 k-points sampled with the Monkhorst–Pack scheme.

Conclusion

For the first time, the bandgap of single fluorohectorite nanosheets has been determined, using electron energy-loss spectroscopy (EELS) and DFT calculations. The energy of the bandgap was found experimentally to be in the range of 7.1–8.2 eV, supported by DFT calculations of bandgap at 5.5 eV, which establishes that this ideal high-aspect ratio insulating single nanosheet material has one of the largest bandgap in the world. These nanosheets (0.95-nm thin, aspect ratio up to 50,000) can be used as an insulating nanosheet for deposition of graphene and various (semi)conductive 2D materials, which make them interesting candidates for fabrication of 2D-based electronic heterostructures by self-assembly or manually. The information provided in this work can be essential for the growing community focused on the study of 2D materials and their wide range of applications.