Skip to main content
SpringerLink
Log in

Using Lattice Energies to Model the Physical/Chemical Behavior of a Doped Refractory Oxide

  • Refractories
  • Published:
MRS Bulletin Aims and scope Submit manuscript

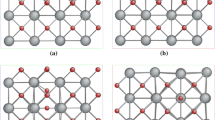
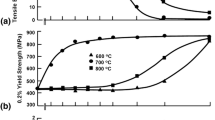
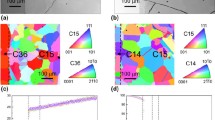
Conclusions

The calculated lattice energies apparently reflect the hydration susceptibility as a function of dopant species. While the experimental work done in this area is limited, what is reported in the literature supports the present work. The calculated lattice energies are also a function of dopant concentration. Experimental results would be useful in determining the accuracy of this observation. A degree of ordering has been imposed due to the relatively small supercell used in this study. The 2×2×2 models used in these studies imposed a high degree of order on the defects in the system. We are in the process of investigating the dependence of doped lattice energy estimates on the size of the supercell. We plan to use a supercell which contains 64 unit cells, which will open up the number of possible defect configurations. We also plan to correlate future results to systematic measurements of hydration susceptibility, sintering behavior, surface microhardness, as well as elasticity and strength properties. A more accurate portrayal of these structures will require a significant amount of computing time. Indications are that these types of studies can be profitable.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. M.J. Gildersleeve and R.J. Brook, “Fast Firing of Sea-Water Magnesia Materials,” Trans J. Brit. Ceram. Soc. 83 (1984) p. 154–157.

    CAS  Google Scholar 

  2. B.L. Fletched, J.R. Stevenson, and A. Whitaker, “Phase Equilibria in the System CaO-MgO-B2O3 at 900°C,” Trans J. Brit. Ceram. Soc. 69 (1970) p. 95–97.

    Article  Google Scholar 

  3. H.J.S. Kriek, W.F. Ford, and J. White, “The Effect of Additions on the Sintering and Dead-Burning of Magnesia,” Trans. Brit. Ceram. Soc. 58 (1959) p. 1–34.

    CAS  Google Scholar 

  4. E.A. Hyleraas, “Gleichgewichtslage der Atome, Doppelbrechung und Optisches Drehungsvermogen von β-Quartz,” Z. Physik 44 (1927) p. 871–876.

    Article  Google Scholar 

  5. Q.C. Johnson and D.H. Templeton, “Madelung Constants for Several Structures,” J. Chem. Phys. 34 (1961) p. 2004–2007.

    Article  CAS  Google Scholar 

  6. R.F. Giese, Jr., “Electrostatic Energy of Columbite and Ixiolite,” Nature 256 p. 31–32.

  7. G.E. Brown and P.M. Fenn, “Structure Energies of the Alkali Feldspars,” Physics and Chemistry of Minerals 4 (1979) p. 83–100.

    Article  CAS  Google Scholar 

  8. J.E. Post and C.W. Burnham, “Disordering on High Albite-Insights from Electrostatic Energy Minimizations,” Geological Soc. of America Absts. with Programs 16 (1984) p. 625.

    Google Scholar 

  9. J.E. Post and C.W. Burnham, “Ionic Modeling of Mineral Structures and Energies in the Electron Gas Approximarion-TiO2 Polymorphs, Quartz, Forsterite, Diopside,” American Mineralogist 71 (1986) p. 142–150.

    CAS  Google Scholar 

  10. Chamberlain, “Scapolite-Alkali Atom Configurations, Antiphase Domains, and Compositional Variations,” American Mineralogist 70 (1985) p. 134–140.

    CAS  Google Scholar 

  11. R.E. Cohen and C.W. Burnham, “Energetics of Ordering in Aluminous Pyroxines,” American Mineralogist 70 (1985) p. 559–567.

    CAS  Google Scholar 

  12. J.E. Post and C.W. Burnham, “Modeling Tunnel-Cation Displacements in Hollandites Using Structure-Energy Calculations,” American Mineralogist 71 (1986) p. 1178–1185.

    CAS  Google Scholar 

  13. W.R. Busing, “WMIN, A Computer Program to Model Molecules and Crystals in Terms of Potential Energy Functions,” U.S. National Technical Information Service, ORNL-5747.

  14. F. Bertaut, “L’Energie Electrostatique de Reseaux Ioniques,” J. Phys. Radium 13 (1952) p. 499–505.

    Article  CAS  Google Scholar 

  15. C. Kittel, Introduction to Solid State Physics, 5th ed. (1976) p. 88.

  16. T.L. Gilbert, “Soft-Sphere Model for Closed Shell Atoms and Ions,” J. Chem. Phys. 49 (1968) p. 2640.

    Article  CAS  Google Scholar 

  17. P. Kofstad, Nonstoichiometry, Diffusion, and Electrical Conductivity in Binary Metal Oxides (Wiley Interscience, John Wiley & Sons, NY, 1972).

    Google Scholar 

  18. C. Butterfield and E.H. Carlson, “Ionic Soft Sphere Parameters from Hartree-Fock-Slater Calculations,” J. Chem. Phys. 56 (1972) p. 4907–4911.

    Article  CAS  Google Scholar 

  19. G.K. Layden and M.C. McQurrie, “Effect of Minor Additions on Sintering of MgO,” J. Amer. Ceram. Soc. 42(2) (1959) p. 89–92.

    Article  CAS  Google Scholar 

  20. J.W. Nelson and I.B. Cutler, “Effect of Oxide Additions on Sintering of MgO,” J. Amer. Ceram. Soc. 41(10) (1958) p. 406–409.

    Article  CAS  Google Scholar 

Download references

Authors
  1. Scott A. Howard
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Soon-Ho Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Robert E. Moore
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Howard, S.A., Lee, SH. & Moore, R.E. Using Lattice Energies to Model the Physical/Chemical Behavior of a Doped Refractory Oxide. MRS Bulletin 14, 60–64 (1989). https://doi.org/10.1557/S0883769400061224

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1557/S0883769400061224

Search

Navigation