Skip to main content
SpringerLink
Log in

A model for front evolution with a nonlocal growth rate

  • Rapid Communications
  • Published:
Journal of Materials Research Aims and scope Submit manuscript

Abstract

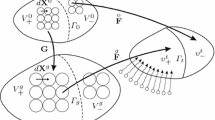
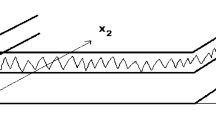
In this paper we provide a new mathematical model for front propagation with a nonlocal growth law in any space dimension. Such a problem arises in composite fabrication using the vapor infiltration process and in other physical problems involving transport and reaction. Our model, based on the level set equation coupled with a boundary value problem of the Laplace equation, is an Eulerian formulation, which allows robust treatment for topological changes such as merging and formation of pores without artificially tracking them. When applied to the fabrication of continuous filament ceramic matrix composites using chemical vapor infiltration, this model accurately predicts not only residual porosity but also the precise locations and shapes of all pores.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. M. Avrami, J. Chem. Phys. 7, 1103–1112 (1939); 8, 212–224 (1940).

    Article  CAS  Google Scholar 

  2. T.M. Besmann, B.W. Sheldon, R.A. Lowden, and D.P. Stinton, Science 253, 1104 (1991).

    Article  CAS  Google Scholar 

  3. M.G. Crandall and P.L. Lions, Trans. Am. Math. Soc. 277, 1–42, (1983).

  4. L.C. Evans, Partial Differential Equations (Amer. Math. Soc., Providence, RI, 1998).

    Google Scholar 

  5. W.A. Johnson and P.A. Mehl, Trans. Am. Inst. Min. Metall. Eng. 135, 416 (1939).

    Google Scholar 

  6. A.N. Kolmogorov, Bull. Acad. Sci., USSR Phys. Ser 1, 355 (1937).

    Google Scholar 

  7. S. Osher and J.A. Sethian, J. Comp. Phys. 78, 12–49 (1988).

    Article  Google Scholar 

  8. M. Sahimi, Applications of Percolation Theory (Taylor & Francis, London, 1994).

    Book  Google Scholar 

  9. J.A. Sethian, Level Set Methods (Cambridge University Press, New York, 1996).

  10. S. Sotirchos and S. Zarkanitis, Chem. Eng. Sci. 48(8), 1487–1502 (1993).

  11. D. Stauffer and A. Aharony, Introduction to Percolation Theory (Taylor & Francis, London, 1992).

    Google Scholar 

  12. G.B. Whitham, Linear and Nonlinear Waves (John Wiley & Sons, New York, 1974).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics, Georgia Institute of Technology, 30332, Atlanta, Georgia, USA

    Shi Jin

  2. Department of Chemical Engineering, University of Louisville, 40292, Louisville, Kentucky, USA

    Xuelei Wang & Thomas L. Starr

Authors
  1. Shi Jin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xuelei Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Thomas L. Starr
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jin, S., Wang, X. & Starr, T.L. A model for front evolution with a nonlocal growth rate. Journal of Materials Research 14, 3829–3832 (1999). https://doi.org/10.1557/JMR.1999.0515

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1557/JMR.1999.0515

Search

Navigation