Skip to main content
SpringerLink
Log in

Analysis of ball-indentation load-depth data: Part I. Determining elastic modulus

  • Articles
  • Published:
Journal of Materials Research Aims and scope Submit manuscript

Abstract

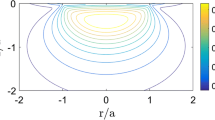
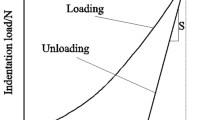
Analysis of ball-indentation process was made by the finite element (FE) method. A series of indentation FE analyses were made on materials with different elastic modulus (E), and a simple relationship between E and the load-depth (F-h) unloading data is presented. In order to check for the influence of other material properties, thorough research has been performed, introducing a combination of response surface (RS) and FE analysis. As a result, a relationship between the indentation unloading slope, E, and the strain hardening exponent was derived. Also, the indenter compliance effect has been investigated. The indenter compliance correction was calculated and applied to the experimentally measured F-h results. Experimental testing was made on three materials with essentially different elastic moduli. Comparison of the results obtained by newly developed equations with the results from other well-known equations is also presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. H. Hertz, Miscellaneous Papers by H. Hertz, edited by Jones and Schott (Macmillan, London, 1896).

    Google Scholar 

  2. D. Tabor, The Hardness of Metals (Clarendon Press, Oxford, 1951).

    Google Scholar 

  3. I. N. Sneddon, Int. J. Eng. Sci. 3, 47–57 (1965).

    Article  Google Scholar 

  4. I. N. Sneddon, Proc. Cambridge Philos. Soc. 42, 29 (1946).

    Article  Google Scholar 

  5. I. N. Sneddon, Proc. Cambridge Philos. Soc. 44, 429 (1948).

    Google Scholar 

  6. G. M. Pharr, W. C. Oliver, and F. R. Brotzen, J. Mater. Res. 7, 613–617 (1992).

    Article  CAS  Google Scholar 

  7. W. C. Oliver and G. M. Pharr, J. Mater. Res. 7, 1564–1583 (1992).

    Article  CAS  Google Scholar 

  8. H. A. Francis, Trans. ASME, J. Eng. Mater. Technol., 272–281 (July 1976).

  9. A. K. Bhattacharya and W. D. Nix, Int. J. Solids Structures 27 (8), 1047–1058 (1991).

    Article  Google Scholar 

  10. A. E. Giannakopoulos, P. L. Larson, and R. Vestergaard, Int. J. Solids Structures 31 (19), 2679–2708 (1994).

    Article  Google Scholar 

  11. B. Taljat, Determining Stress-Strain Curves of Metals by Nondestructive Continuous Ball-Indentation Method, Ph.D. Thesis, University of Ljubljana, Slovenia.

  12. S. P. Timoshenko and J. N. Goodier, Theory of Elasticity, 3rd ed. (McGraw-Hill, New York, 1970).

    Google Scholar 

  13. R. H. Myers, Response Surface Methodology (Allyn and Bacon Inc., Boston, New York, 1971).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Oak Ridge National Laboratory, Metals and Ceramics Division, 37831-6140, Oak Ridge, Tennessee, USA

    B. Taljat, T. Zacharia & F. M. Haggag

  2. Currently at Advanced Technology Corporation, 115 Clemson Drive, 37830-7665, Oak Ridge, Tennessee, USA

    F. M. Haggag

Authors
  1. B. Taljat
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. Zacharia
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. F. M. Haggag
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Taljat, B., Zacharia, T. & Haggag, F.M. Analysis of ball-indentation load-depth data: Part I. Determining elastic modulus. Journal of Materials Research 12, 965–974 (1997). https://doi.org/10.1557/JMR.1997.0137

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1557/JMR.1997.0137

Search

Navigation