Abstract
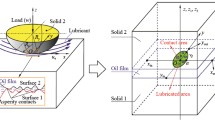
The numerical simulation of temperature distribution of point contacts in mixed lubrication is presented. The calculating includes two steps. First, temperature rises on two surfaces are obtained by a temperature integration method of transient point heat source. Second, the partition coefficients of heat flux are determined by matching the temperature of two surfaces. Similar to the calculation of elastic deformation, double linear interpolation function is used to get a better accuracy, and moving grid method is used to increase the efficiency of the computation. Due to the symmetry of influence coefficient matrix in the direction perpendicular to the velocity, storage and computational work are further reduced by 50%. Numerical samples validate the algorithm and program. The calculating results of the cases of smooth surface and isotropic sinusoidal surface are presented.
Similar content being viewed by others
Abbreviations
- a :
-
Hertzian contact radius
- c :
-
specific heat of solid
- C1, C2:
-
influence coefficients of body 1 and body 2. f. heat partition coefficient
- h, \(\bar h\):
-
oil film thickness and its dimensionless parameter, \(\bar h = h/a\)
- Ks, Kf:
-
thermal conductivities of solid and fluid
- p, \(\bar p\):
-
pressure and its dimensionless parameter, \(\bar p = p/p_h \)
- P h :
-
maximum Hertzian pressure, q, \(\bar q\), heat flux density and its dimensionless parameter, q=μpV s , \(\bar q = \mu \bar p\bar V_s \); S=π 3/2 K s/K f
- t, \(\bar t\):
-
time and its dimensionaless parameter, \(\bar t = t \cdot 4\alpha /a^2 \)
- \(T_{1b} ,T_{2b} ,\bar T_{1b} ,\bar T_{2b} \) :
-
bulk temperatures of body 1 and body 2 and the dimensionless forms, \(\bar T = T \cdot \pi ^{3/2} \rho c/(2p_h )\)
- \(\Delta \bar T_1 ,\Delta \bar T_2 \) :
-
dimensionless temperatures rises of body 1 and body 2; \(u = \bar t - \bar t'\)
- \(V_1 ,V_2 ,\bar V_1 ,\bar V_2 \) :
-
velocities of body 1 and body 2 and the dimensionless forms \(\bar V = Va/(4\alpha )\)
- V s , \(\bar V_s \):
-
sliding velocity and its dimensionless parameter, V a=|V 1−V 2|, \(\bar V_s = \left| {\bar V_1 - \bar V_2 } \right|\)
- x, y, \(\bar x,\bar y\):
-
Cartesian coordinates and nondimensional, \(\bar x = x/a, \bar y = y/a\)
- \(\Delta \bar x,\Delta \bar y\) :
-
mesh spacing in the direction of \(\bar x\) and \(\bar y\) axis
- α=K g/gc :
-
thermal diffusivity of solid
- μ:
-
friction coefficient
- σ:
-
density of solid
- μ:
-
solution domain
- Pe=Va/2α) :
-
Peclet number
References
Tian Xuefeng, Kennedy, F. E., Contact surface temperature models for finite bodies in dry and boundary lubricated sliding. ASME. Journal of Tribology, 1993, 115(3): 411.
Zhu Dong, Wen Shizhu, A full numerical solution for the thermoelastohydrodynamic problem in elliptical contacts. ASME. Journal of Tribology, 1984, 106(2): 246.
Vilmos, S.: Thermal elastohydrodynamic lubrication of rider rings. ASME, Journal of Tribology, 1984, 106(4): 492–498.
Guo Feng, Yang Peiran, Influence of a ring flat zone in the point contact surface in thermal elastohydyodynamic lubrication. Tribology International 1999, 32: 167.
Carslaw, H. S., Jeager, J. C., Conduction of Heat in Solids, 2nd ed. London: Oxford Press, 1959, 266–270.
Bruggemann, H., Kollmann, F. G., A numerical solution of the thermal elastohydrodynamic lubrication in an elliptical contact, ASME, Journal of Tribology, 1982, 104(3): 392.
Ghosh, M. K., Harmrock, B. J., Thermal elastohydrodynamic lubrication of line contacts, ASLE Transaction, 1984, 28(2): 159.
Zhu, D., Cheng, H. S., An analysis and computational procedure for EHL film thickness, friction and flash temperature in line and point contacts, Tribology Transaction, 1989, 32(3): 364.
Blok, H. Theoretical study of temperature rise at surfaces of actual contact under oiliness conditions. Proc. General discussion on lubrication, London: Inst. Mech. Engrs., 1937, 14: 222.
Francis, H. A., Interfacial temperature distribution within a sliding Hertzian contact. ASLE Transaction, 1970, 14(1): 41.
Tian Xuefeng, Kennedy, F.E.: Maximum and average flash temperature in sliding contacts. ASME. Journal of Tribology 1994, 116: 167.
Zhai Xuejun, Chang, L., A transient thrmal model for mixed-film contacts, Tribology Transaction, 2000, 43(3): 427.
Qiu, Liangheng, Cheng, H. S., Temperature rise simulation of three-dimensional rough surface in mixed lubricated contact, ASME. Journal of Tribology, 1998, 120(2): 310.
Hu Yuanzhong, Zhu Dong, A full numerical solution to the mixed lubrication in point contact, Tribology Transaction, 2000. 44(1): 1.
Ren Ning, Lee, S. C., Contact simulation of three dimensional rough surfaces using moving grid method. ASME, Journal of Tribology, 1993, 115(4): 597.
Lai, W. T., Cheng, H. S., Temperature analysis in lubricated simple sliding rough contacts. ASLE Transaction 1984, 128(3): 302.
Gao, Jianjun, Lee, S. C., Ai Xiaolan et al., An FFT-based transient flash temperature model of general three-dimensional rough surface contacts. ASME. Journal of Tribology, 2000, 122(3): 519.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Liu, Y., Hu, Y., Wang, W. et al. Simulation of temperature distribution of point contacts in mixed lubrication. Sci. China Ser. E-Technol. Sci. 45, 365–372 (2002). https://doi.org/10.1360/02ye9043
Received:
Issue Date:
DOI: https://doi.org/10.1360/02ye9043