Abstract
Equal-arm detectors of gravitational radiation allow phase measurements many orders of magnitude below the intrinsic phase stability of the laser injecting light into their arms. This is because the noise in the laser light is common to both arms, experiencing exactly the same delay, and thus cancels when it is differenced at the photo detector. In this situation, much lower level secondary noises then set the overall performance. If, however, the two arms have different lengths (as will necessarily be the case with space-borne interferometers), the laser noise experiences different delays in the two arms and will hence not directly cancel at the detector. In order to solve this problem, a technique involving heterodyne interferometry with unequal arm lengths and independent phase-difference readouts has been proposed. It relies on properly time-shifting and linearly combining independent Doppler measurements, and for this reason it has been called time-delay interferometry (TDI).
This article provides an overview of the theory, mathematical foundations, and experimental aspects associated with the implementation of TDI. Although emphasis on the application of TDI to the Laser Interferometer Space Antenna (LISA) mission appears throughout this article, TDI can be incorporated into the design of any future space-based mission aiming to search for gravitational waves via interferometric measurements. We have purposely left out all theoretical aspects that data analysts will need to account for when analyzing the TDI data combinations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Breakthroughs in modern technology have made possible the construction of extremely large interferometers both on the ground and in space for the detection and observation of gravitational waves (GWs). Several ground-based detectors around the globe have been operational for several years, and are now in the process of being upgraded to achieve even higher sensitivities. These are the LIGO and VIRGO interferometers, which have arm lengths of 4 km and 3 km, respectively, and the GEO and TAMA interferometers with arm lengths of 600 m and 300 m, respectively. These upgraded detectors will operate in the high frequency range of GWs of ∼ 1 Hz to a few kHz. A natural limit occurs on decreasing the lower frequency cut-off because it is not practical to increase the arm lengths on ground and also because of the gravity gradient noise which is difficult to eliminate below 1 Hz. Thus the ground based interferometers will not be sensitive below this limiting frequency. But, on the other hand, in the cosmos there exist interesting astrophysical GW sources which emit GWs below this frequency such as the galactic binaries, massive and super-massive black-hole binaries, etc. If we wish to observe these sources, we need to go to lower frequencies. The solution is to build an interferometer in space, where such noises will be absent and allow the detection of GWs in the low frequency regime. The Laser Interferometer Space Antenna (LISA) mission, and more recent variations of its design [13, 35], is the typical example of a space-based interferometer aiming to detect and study gravitational radiation in the millihertz band. In order to make such observations LISA relied on coherent laser beams exchanged between three identical spacecraft forming a giant (almost) equilateral triangle of side 5 × 106 km to observe and detect low frequency cosmic GWs. Ground- and space-based detectors will complement each other in the observation of GWs in an essential way, analogous to the way optical, radio, X-ray, γ-ray, etc. observations do for the electromagnetic spectrum. As these detectors begin to make their observations, a new era of gravitational astronomy is on the horizon and a radically different view of the Universe is expected to emerge.
The astrophysical sources observable in the mHz band include galactic binaries, extra-galactic super-massive black-hole binaries and coalescences, and stochastic GW background from the early Universe. Coalescing binaries are one of the important sources in this frequency region. These include galactic and extra galactic stellar mass binaries, and massive and super-massive blackhole binaries. The frequency of the GWs emitted by such a system is twice its orbital frequency. Population synthesis studies indicate a large number of stellar mass binaries in the frequency range below 2–3 mHz [4, 34]. In the lower frequency range (≤ 1 mHz) there is a large number of such unresolvable sources in each of the frequency bins. These sources effectively form a stochastic GW background referred to as binary confusion noise.
Massive black-hole binaries are interesting both from the astrophysical and theoretical points of view. Coalescences of massive black holes from different galaxies after their merger during growth of the present galaxies would provide unique new information on galaxy formation. Coalescence of binaries involving intermediate mass black holes could help to understand the formation and growth of massive black holes. The super-massive black-hole binaries are strong emitters of GWs and these spectacular events can be detectable beyond red-shift of z = 10. These systems would help to determine the cosmological parameters independently. And, just as the cosmic microwave background is left over from the big bang, so too should there be a background of gravitational waves. Unlike electromagnetic waves, gravitational waves do not interact with matter after a few Planck times after the big bang, so they do not thermalize. Their spectrum today, therefore, is simply a red-shifted version of the spectrum they formed with, which would throw light on the physical conditions at the epoch of the early Universe.
Interferometric non-resonant detectors of gravitational radiation with frequency content f1 < f < fu (f1, fu being respectively the lower and upper frequency cut-offs characterizing the detector’s operational bandwidth) use a coherent train of electromagnetic waves (of nominal frequency ν0 ≫ fu) folded into several beams, and at one or more points where these intersect, monitor relative fluctuations of frequency or phase (homodyne detection). The observed low-frequency fluctuations are due to several causes:
-
1.
frequency variations of the source of the electromagnetic signal about ν0,
-
2.
relative motions of the electromagnetic source and the mirrors (or amplifying transponders) that do the folding,
-
3.
temporal variations of the index of refraction along the beams, and
-
4.
according to general relativity, to any time-variable gravitational fields present, such as the transverse-traceless metric curvature of a passing plane gravitational-wave train.
To observe gravitational waves in this way, it is thus necessary to control, or monitor, the other sources of relative frequency fluctuations, and, in the data analysis, to use optimal algorithms based on the different characteristic interferometer responses to gravitational waves (the signal) and to the other sources (the noise) [55]. By comparing phases of electromagnetic beams referenced to the same frequency generator and propagated along non-parallel equal-length arms, frequency fluctuations of the frequency reference can be removed, and gravitational-wave signals at levels many orders of magnitude lower can be detected.
In the present single-spacecraft Doppler tracking observations, for instance, many of the noise sources can be either reduced or calibrated by implementing appropriate microwave frequency links and by using specialized electronics [52], so the fundamental limitation is imposed by the frequency (time-keeping) fluctuations inherent to the reference clock that controls the microwave system. Hydrogen maser clocks, currently used in Doppler tracking experiments, achieve their best performance at about 1000 s integration time, with a fractional frequency stability of a few parts in 10−16. This is the reason why these one-arm interferometers in space (which have one Doppler readout and a “3-pulse” response to gravitational waves [14]) are most sensitive to mHz gravitational waves. This integration time is also comparable to the microwave propagation (or “storage”) time 2L/c to spacecraft en route to the outer solar system (for example L ≃ 5−8 AU for the Cassini spacecraft) [52].
Low-frequency interferometric gravitational-wave detectors in solar orbits, such as the LISA mission and the currently considered eLISA/NGO mission [5, 13, 35], have been proposed to achieve greater sensitivity to mHz gravitational waves. However, since the armlengths of these space-based interferometers can differ by a few percent, the direct recombination of the two beams at a photo detector will not effectively remove the laser frequency noise. This is because the frequency fluctuations of the laser will be delayed by different amounts within the two arms of unequal length. In order to cancel the laser frequency noise, the time-varying Doppler data must be recorded and post-processed to allow for arm-length differences [53]. The data streams will have temporal structure, which can be described as due to many-pulse responses to δ-function excitations, depending on time-of-flight delays in the response functions of the instrumental Doppler noises and in the response to incident plane-parallel, transverse, and traceless gravitational waves.
Although the theory of TDI can be used by any future space-based interferometer aiming to detect gravitational radiation, this article will focus on its implementation by the LISA mission [5].
The LISA design envisioned a constellation of three spacecraft orbiting the Sun. Each spacecraft was to be equipped with two lasers sending beams to the other two (∼ 0.03 AU away) while simultaneously measuring the beat frequencies between the local laser and the laser beams received from the other two spacecraft. The analysis of TDI presented in this article will assume a successful prior removal of any first-order Doppler beat notes due to relative motions [57], giving six residual Doppler time series as the raw data of a stationary time delay space interferometer. Following [51, 2, 10], we will regard LISA not as constituting one or more conventional Michelson interferometers, but rather, in a symmetrical way, a closed array of six one-arm delay lines between the test masses. In this way, during the course of the article, we will show that it is possible to synthesize new data combinations that cancel laser frequency noises, and estimate achievable sensitivities of these combinations in terms of the separate and relatively simple single arm responses both to gravitational wave and instrumental noise (cf. [51, 2, 10]).
In contrast to Earth-based interferometers, which operate in the long-wavelength limit (LWL) (arm lengths ≪ gravitational wavelength ∼ c/f0, where f0 is a characteristic frequency of the GW), LISA does not operate in the LWL over much of its frequency band. When the physical scale of a free mass optical interferometer intended to detect gravitational waves is comparable to or larger than the GW wavelength, time delays in the response of the instrument to the waves, and travel times along beams in the instrument, cannot be ignored and must be allowed for in computing the detector response used for data interpretation. It is convenient to formulate the instrumental responses in terms of observed differential frequency shifts — for short, Doppler shifts — rather than in terms of phase shifts usually used in interferometry, although of course these data, as functions of time, are inter-convertible.
This second review article on TDI is organized as follows. In Section 2 we provide an overview of the physical and historical motivations of TDI. In Section 3 we summarize the one-arm Doppler transfer functions of an optical beam between two carefully shielded test masses inside each spacecraft resulting from (i) frequency fluctuations of the lasers used in transmission and reception, (ii) fluctuations due to non-inertial motions of the spacecraft, and (iii) beam-pointing fluctuations and shot noise [15]. Among these, the dominant noise is from the frequency fluctuations of the lasers and is several orders of magnitude (perhaps 7 or 8) above the other noises. This noise must be very precisely removed from the data in order to achieve the GW sensitivity at the level set by the remaining Doppler noise sources which are at a much lower level and which constitute the noise floor after the laser frequency noise is suppressed. We show that this can be accomplished by shifting and linearly combining the twelve one-way Doppler data measured by LISA. The actual procedure can easily be understood in terms of properly defined time-delay operators that act on the one-way Doppler measurements. In Section 4 we develop a formalism involving the algebra of the time-delay operators which is based on the theory of rings and modules and computational commutative algebra. We show that the space of all possible interferometric combinations canceling the laser frequency noise is a module over the polynomial ring in which the time-delay operators play the role of the indeterminates [10]. In the literature, the module is called the module of syzygies [3, 29]. We show that the module can be generated from four generators, so that any data combination canceling the laser frequency noise is simply a linear combination formed from these generators. We would like to emphasize that this is the mathematical structure underlying TDI for LISA.
Also in Section 4 specific interferometric combinations are derived, and their physical interpretations are discussed. The expressions for the Sagnac interferometric combinations (α, β, γ, ζ) are first obtained; in particular, the symmetric Sagnac combination ζ, for which each raw data set needs to be delayed by only a single arm transit time, distinguishes itself against all the other TDI combinations by having a higher order response to gravitational radiation in the LWL when the spacecraft separations are equal. We then express the unequal-arm Michelson combinations (X, Y, Z) in terms of the α, β, γ, and ζ combinations with further transit time delays. One of these interferometric data combinations would still be available if the links between one pair of spacecraft were lost. Other TDI combinations, which rely on only four of the possible six inter-spacecraft Doppler measurements (denoted P, E, and U) are also presented. They would of course be quite useful in case of potential loss of any two inter-spacecraft Doppler measurements.
TDI so formulated presumes the spacecraft-to-spacecraft light-travel-times to be constant in time, and independent from being up- or down-links. Reduction of data from moving interferometric laser arrays in solar orbit will in fact encounter non-symmetric up- and downlink light time differences that are significant, and need to be accounted for in order to exactly cancel the laser frequency fluctuations [44, 7, 45, 41, 9]. In Section 5 we show that, by introducing a set of non-commuting time-delay operators, there exists a quite general procedure for deriving generalized TDI combinations that account for the effects of time-dependence of the arms. Using this approach it is possible to derive “flex-free” expression for the unequal-arm Michelson combinations X1, and obtain the generalized expressions for all the TDI combinations [58]. Alternatively, a rigorous mathematical formulation can be given in terms of rings and modules. But because of the non-commutativity of operators the polynomial ring is non-commutative. Thus the algebraic problem becomes extremely complex and a general solution seems difficult to obtain [9]. But we show that for the special case when one arm of LISA is dysfunctional a plethora of solutions can be found [11]. Such a possibility must be envisaged because of reasons such as technical failure or even operating costs.
In Section 6 we address the question of maximization of the LISA signal-to-noise-ratio (SNR) to any gravitational-wave signal present in its data. This is done by treating the SNR as a functional over the space of all possible TDI combinations. As a simple application of the general formula we have derived, we apply our results to the case of sinusoidal signals randomly polarized and randomly distributed on the celestial sphere. We find that the standard LISA sensitivity figure derived for a single Michelson interferometer [15, 38, 40] can be improved by a factor of \(\sqrt 2\) in the low-part of the frequency band, and by more than \(\sqrt 3\) in the remaining part of the accessible band. Further, we also show that if the location of the GW source is known, then as the source appears to move in the LISA reference frame, it is possible to optimally track the source, by appropriately changing the data combinations during the course of its trajectory [38, 39]. As an example of such type of source, we consider known binaries within our own galaxy.
In Section 7, we finally address aspects of TDI of more practical and experimental nature, and provide a list of references where more details about these topics can be found. It is worth mentioning that, as of today, TDI has already gone through several successful experimental tests [8, 32, 48, 33, 25] and that it has been endorsed by the eLISA/NGO [13, 35] project as its baseline technique for achieving its required sensitivity to gravitational radiation.
We emphasize that, although this article will use as baseline mission reference the LISA mission, the results here presented can easily be extended to other space mission concepts.
2 Physical and Historical Motivations of TDI
Equal-arm interferometer detectors of gravitational waves can observe gravitational radiation by canceling the laser frequency fluctuations affecting the light injected into their arms. This is done by comparing phases of split beams propagated along the equal (but non-parallel) arms of the detector. The laser frequency fluctuations affecting the two beams experience the same delay within the two equal-length arms and cancel out at the photodetector where relative phases are measured. This way gravitational-wave signals of dimensionless amplitude less than 10−20 can be observed when using lasers whose frequency stability can be as large as roughly a few parts in 10−13.
If the arms of the interferometer have different lengths, however, the exact cancellation of the laser frequency fluctuations, say C(t), will no longer take place at the photodetector. In fact, the larger the difference between the two arms, the larger will be the magnitude of the laser frequency fluctuations affecting the detector response. If L1 and L2 are the lengths of the two arms, it is easy to see that the amount of laser relative frequency fluctuations remaining in the response is equal to (units in which the speed of light c = 1)
In the case of a space-based interferometer such as LISA, whose lasers are expected to display relative frequency fluctuations equal to about \({10^{- 13}}/\sqrt {{\rm{Hz}}}\) in the mHz band, and whose arms will differ by a few percent [5, 13, 35], Eq. (1) implies the following expression for the amplitude of the Fourier components of the uncanceled laser frequency fluctuations (an over-imposed tilde denotes the operation of Fourier transform):
At f = 10−3 Hz, for instance, and assuming ∣L1 − L2∣ ≃ 0.5 s, the uncanceled fluctuations from the laser are equal to \(6.3 \times {10^{- 16}}/\sqrt {{\rm{Hz}}}\). Since the LISA sensitivity goal was about \({10^{- 20}}/\sqrt {{\rm{Hz}}}\) in this part of the frequency band, it is clear that an alternative experimental approach for canceling the laser frequency fluctuations is needed.
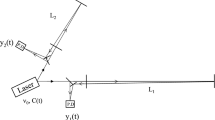
A first attempt to solve this problem was presented by Faller et al. [17, 19, 18], and the scheme proposed there can be understood through Figure 1. In this idealized model the two beams exiting the two arms are not made to interfere at a common photodetector. Rather, each is made to interfere with the incoming light from the laser at a photodetector, decoupling in this way the phase fluctuations experienced by the two beams in the two arms. Now two Doppler measurements are available in digital form, and the problem now becomes one of identifying an algorithm for digitally canceling the laser frequency fluctuations from a resulting new data combination.
Light from a laser is split into two beams, each injected into an arm formed by pairs of free-falling mirrors. Since the length of the two arms, L1 and L2, are different, now the light beams from the two arms are not recombined at one photo detector. Instead each is separately made to interfere with the light that is injected into the arms. Two distinct photo detectors are now used, and phase (or frequency) fluctuations are then monitored and recorded there.
The algorithm they first proposed, and refined subsequently in [24], required processing the two Doppler measurements, say y1(t) and y2(t), in the Fourier domain. If we denote with h1(t), h2(t) the gravitational-wave signals entering into the Doppler data y1, y2, respectively, and with n1, n2 any other remaining noise affecting y1 and y2, respectively, then the expressions for the Doppler observables y1, y2 can be written in the following form:
From Eqs. (3) and (4) it is important to note the characteristic time signature of the random process C(t) in the Doppler responses y1, y2. The time signature of the noise C(t) in y1(t), for instance, can be understood by observing that the frequency of the signal received at time t contains laser frequency fluctuations transmitted 2L1 s earlier. By subtracting from the frequency of the received signal the frequency of the signal transmitted at time t, we also subtract the frequency fluctuations C(t) with the net result shown in Eq. (3).
The algorithm for canceling the laser noise in the Fourier domain suggested in [17] works as follows. If we take an infinitely long Fourier transform of the data y1, the resulting expression of y1 in the Fourier domain becomes (see Eq. (3))
If the arm length L1 is known exactly, we can use the y1 data to estimate the laser frequency fluctuations \(\tilde C(f)\). This can be done by dividing y1 by the transfer function of the laser noise C into the observable y1 itself. By then further multiplying \({\tilde y_1}/[{e^{4\pi if{L_1}}} - 1]\) by the transfer function of the laser noise into the other observable \({\tilde y_2}\), i.e., \([{e^{4\pi if{L_2}}} - 1]\), and then subtract the resulting expression from \({\tilde y_2}\) one accomplishes the cancellation of the laser frequency fluctuations.
The problem with this procedure is the underlying assumption of being able to take an infinitely long Fourier transform of the data. Even if one neglects the variation in time of the LISA arms, by taking a finite-length Fourier transform of, say, y1(t) over a time interval T, the resulting transfer function of the laser noise C into y1 no longer will be equal to \([{e^{4\pi if{L_1}}} - 1]\). This can be seen by writing the expression of the finite length Fourier transform of y1 in the following way:
where we have denoted with H(t) the function that is equal to 1 in the interval [−T, +T], and zero everywhere else. Eq. (6) implies that the finite-length Fourier transform \(\tilde y_1^T\) of y1(t) is equal to the convolution in the Fourier domain of the infinitely long Fourier transform of y1(t), \({\tilde y_1}\), with the Fourier transform of H(t) [28] (i.e., the “Sinc Function” of width 1/T). The key point here is that we can no longer use the transfer function \([{e^{4\pi if{L_i}}} - 1]\), i = 1, 2, for estimating the laser noise fluctuations from one of the measured Doppler data, without retaining residual laser noise into the combination of the two Doppler data y1, y2 valid in the case of infinite integration time. The amount of residual laser noise remaining in the Fourier-based combination described above, as a function of the integration time T and type of “window function” used, was derived in the appendix of [53]. There it was shown that, in order to suppress the residual laser noise below the LISA sensitivity level identified by secondary noises (such as proof-mass and optical path noises) with the use of the Fourier-based algorithm an integration time of about six months was needed.
A solution to this problem was suggested in [53], which works entirely in the time-domain. From Eqs. (3) and (4) we may notice that, by taking the difference of the two Doppler data y1(t), y2(t), the frequency fluctuations of the laser now enter into this new data set in the following way:
If we now compare how the laser frequency fluctuations enter into Eq. (7) against how they appear in Eqs. (3) and (4), we can further make the following observation. If we time-shift the data y1(t) by the round trip light time in arm 2, y1(t − 2L2), and subtract from it the data y2(t) after it has been time-shifted by the round trip light time in arm 1, y2(t − 2L1), we obtain the following data set:
In other words, the laser frequency fluctuations enter into y1(t)−y2(t) and y1(t−2L2)−y2(t−2L1) with the same time structure. This implies that, by subtracting Eq. (8) from Eq. (7) we can generate a new data set that does not contain the laser frequency fluctuations C(t),
The expression above of the X combination shows that it is possible to cancel the laser frequency noise in the time domain by properly time-shifting and linearly combining Doppler measurements recorded by different Doppler readouts. This in essence is what TDI amounts to.
In order to gain a better physical understanding of how TDI works, let’s rewrite the above X combination in the following form
where we have simply rearranged the terms in Eq. (9 [45].
Equation (10) shows that X is the difference of two sums of relative frequency changes, each corresponding to a specific light path (the continuous and dashed lines in Figure 2). The continuous line, corresponding to the first square-bracket term in Eq. (10), represents a light-beam transmitted from spacecraft 1 and made to bounce once at spacecraft 3 and 2 respectively. Since the other beam (dashed line) experiences the same overall delay as the first beam (although by bouncing off spacecraft 2 first and then spacecraft 3) when they are recombined they will cancel the laser phase fluctuations exactly, having both experienced the same total delays (assuming stationary spacecraft). For this reason the combination X can be regarded as a synthesized (via TDI) zero-area Sagnac interferometer, with each beam experiencing a delay equal to (2L1 + 2L2). In reality, there are only two beams in each arm (one in each direction) and the lines in Figure 2 represent the paths of relative frequency changes rather than paths of distinct light beams.
In the following sections we will further elaborate and generalize TDI to the realistic LISA configuration.
3 Time-Delay Interferometry
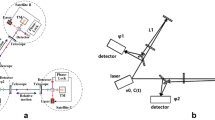
The description of TDI for LISA is greatly simplified if we adopt the notation shown in Figure 3, where the overall geometry of the LISA detector is defined. There are three spacecraft, six optical benches, six lasers, six proof-masses, and twelve photodetectors. There are also six phase difference data going clock-wise and counter-clockwise around the LISA triangle. For the moment we will make the simplifying assumption that the array is stationary, i.e., the back and forth optical paths between pairs of spacecraft are simply equal to their relative distances [44, 7, 45, 58].
Several notations have been used in this context. The double index notation recently employed in [45], where six quantities are involved, is self-evident. However, when algebraic manipulations are involved the following notation seems more convenient to use. The spacecraft are labeled 1, 2, 3 and their separating distances are denoted L1, L2, L3, with Li being opposite spacecraft i. We orient the vertices 1, 2, 3 clockwise in Figure 3. Unit vectors between spacecraft are \({\hat n_i}\), oriented as indicated in Figure 3. We index the phase difference data to be analyzed as follows: The beam arriving at spacecraft has subscript i and is primed or unprimed depending on whether the beam is traveling clockwise or counter-clockwise (the sense defined here with reference to Figure 3) around the LISA triangle, respectively. Thus, as seen from the figure, s1 is the phase difference time series measured at reception at spacecraft 1 with transmission from spacecraft 2 (along L3).
Similarly, s′1 is the phase difference series derived from reception at spacecraft 1 with transmission from spacecraft 3. The other four one-way phase difference time series from signals exchanged between the spacecraft are obtained by cyclic permutation of the indices: 1 → 2 → 3 → 1. We also adopt a notation for delayed data streams, which will be convenient later for algebraic manipulations. We define the three time-delay operators \({{\mathcal D}_i},i = 1,2,3\) where for any data stream x(t)
where Li, i = 1, 2, 3, are the light travel times along the three arms of the LISA triangle (the speed of light c is assumed to be unity in this article). Thus, for example, \({{\mathcal D}_{2{s_1}}}(t) = {s_1}(t - {L_2}),{{\mathcal D}_2}{{\mathcal D}_{3{s_1}}}(t) = {s_1}(t - {L_2} - {L_3}) = {{\mathcal D}_3}{{\mathcal D}_{2{s_1}}}(t)\), etc. Note that the operators commute here. This is because the arm lengths have been assumed to be constant in time. If the Li are functions of time then the operators no longer commute [7, 58], as will be described in Section 4. Six more phase difference series result from laser beams exchanged between adjacent optical benches within each spacecraft; these are similarly indexed as τi, τ′i, i = 1, 2, 3. The proof-mass-plus-optical-bench assemblies for LISA spacecraft number 1 are shown schematically in Figure 4. The photo receivers that generate the data s1, s′1, τ1, and τ′1 at spacecraft 1 are shown. The phase fluctuations from the six lasers, which need to be canceled, can be represented by six random processes pi, p′i, where Pi, p′i are the phases of the lasers in spacecraft i on the left and right optical benches, respectively, as shown in the figure. Note that this notation is in the same spirit as in [57, 45] in which moving spacecraft arrays have been analyzed.
Schematic diagram of proof-masses-plus-optical-benches for a LISA spacecraft. The left-hand bench reads out the phase signals s1 and τ1. The right-hand bench analogously reads out s′1 and τ′1. The random displacements of the two proof masses and two optical benches are indicated (lower case \({\vec \delta _i},{\vec \delta ^{\prime}_i}\) for the proof masses, upper case \({\vec \Delta _i}\), Δ′i for the optical benches).
We extend the cyclic terminology so that at vertex i, i = 1, 2, 3, the random displacement vectors of the two proof masses are respectively denoted by \({\vec \delta _i}(t),{\vec \delta ^{\prime}_i}(t)\), and the random displacements (perhaps several orders of magnitude greater) of their optical benches are correspondingly denoted by \({\vec \Delta _i}(t),\;{\vec \Delta ^{\prime}_i}(t)\) where the primed and unprimed indices correspond to the right and left optical benches, respectively. As pointed out in [15], the analysis does not assume that pairs of optical benches are rigidly connected, i.e., \({\vec \Delta _i} \neq {\vec \Delta ^{\prime}_i}\), in general. The present LISA design shows optical fibers transmitting signals both ways between adjacent benches. We ignore time-delay effects for these signals and will simply denote by μi(t) the phase fluctuations upon transmission through the fibers of the laser beams with frequencies νi, and ν′i. The μi(t) phase shifts within a given spacecraft might not be the same for large frequency differences νi−ν′i For the envisioned frequency differences (a few hundred MHz), however, the remaining fluctuations due to the optical fiber can be neglected [15]. It is also assumed that the phase noise added by the fibers is independent of the direction of light propagation through them. For ease of presentation, in what follows we will assume the center frequencies of the lasers to be the same, and denote this frequency by ν0.
The laser phase noise in s′3 is therefore equal to \({{\mathcal D}_1}{p_2}(t) - {p^{\prime}_3}(t)\). Similarly, since s2 is the phase shift measured on arrival at spacecraft 2 along arm 1 of a signal transmitted from spacecraft 3, the laser phase noises enter into it with the following time signature: \({{\mathcal D}_1}{p^{\prime}_3}(t) - {p_2}(t)\). Figure 4 endeavors to make the detailed light paths for these observations clear. An outgoing light beam transmitted to a distant spacecraft is routed from the laser on the local optical bench using mirrors and beam splitters; this beam does not interact with the local proof mass. Conversely, an incoming light beam from a distant spacecraft is bounced off the local proof mass before being reflected onto the photo receiver where it is mixed with light from the laser on that same optical bench. The inter-spacecraft phase data are denoted s1 and s′1 in Figure 4.
Beams between adjacent optical benches within a single spacecraft are bounced off proof masses in the opposite way. Light to be transmitted from the laser on an optical bench is first bounced off the proof mass it encloses and then directed to the other optical bench. Upon reception it does not interact with the proof mass there, but is directly mixed with local laser light, and again down converted. These data are denoted τ1 and τ′1 in Figure 4.
The expressions for the si, s′i and τi, τ′1 phase measurements can now be developed from Figures 3 and 4, and they are for the particular LISA configuration in which all the lasers have the same nominal frequency ν0, and the spacecraft are stationary with respect to each other.Footnote 1 Consider the s′1(t) process (Eq. (14) below). The photo receiver on the right bench of spacecraft 1, which (in the spacecraft frame) experiences a time-varying displacement \({\vec \Delta ^{\prime}_1}\), measures the phase difference s′1 by first mixing the beam from the distant optical bench 3 in direction \({\hat n_2}\), and laser phase noise p3 and optical bench motion \({\vec \Delta _3}\) that have been delayed by propagation along L2, after one bounce off the proof mass \(({\vec \delta ^{\prime}_1})\), with the local laser light (with phase noise p′1). Since for this simplified configuration no frequency offsets are present, there is of course no need for any heterodyne conversion [57].
In Eq. (13) the τ1 measurement results from light originating at the right-bench laser \(({p^{\prime}_1},\;{\vec \Delta ^{\prime}_1})\), bounced once off the right proof mass \(({\vec \delta ^{\prime}_1})\), and directed through the fiber (incurring phase shift μ1(t)), to the left bench, where it is mixed with laser light (p1). Similarly the right bench records the phase differences s′1 and τ′1. The laser noises, the gravitational-wave signals, the optical path noises, and proof-mass and bench noises, enter into the four data streams recorded at vertex 1 according to the following expressions [15]:
Eight other relations, for the readouts at vertices 2 and 3, are given by cyclic permutation of the indices in Eqs. (12), (13), (14), and (15).
The gravitational-wave phase signal components \(s^{gw}_{i},s\prime^{gw}_{i},i=1,2,3\) in Eqs. (12) and (14) are given by integrating with respect to time the Eqs. (1) and (2) of reference [2], which relate metric perturbations to optical frequency shifts. The optical path phase noise contributions \(s_{i}^{optical\;path},s\prime_{i}^{optical\;path}\) which include shot noise from the low SNR in the links between the distant spacecraft, can be derived from the corresponding term given in [15]. The τi, τ′i measurements will be made with high SNR so that for them the shot noise is negligible.
4 Algebraic Approach for Canceling Laser and Optical Bench Noises
In ground-based detectors the arms are chosen to be of equal length so that the laser light experiences identical delay in each arm of the interferometer. This arrangement precisely cancels the laser frequency/phase noise at the photodetector. The required sensitivity of the instrument can thus only be achieved by near exact cancellation of the laser frequency noise. However, in LISA it is impossible to achieve equal distances between spacecraft, and the laser noise cannot be canceled in this way. It is possible to combine the recorded data linearly with suitable time-delays corresponding to the three arm lengths of the giant triangular interferometer so that the laser phase noise is canceled. Here we present a systematic method based on modules over polynomial rings which guarantees all the data combinations that cancel both the laser phase and the optical bench motion noises.
We first consider the simpler case, where we ignore the optical-bench motion noise and consider only the laser phase noise. We do this because the algebra is somewhat simpler and the method is easy to apply. The simplification amounts to physically considering each spacecraft rigidly carrying the assembly of lasers, beam-splitters, and photodetectors. The two lasers on each spacecraft could be considered to be locked, so effectively there would be only one laser on each spacecraft. This mathematically amounts to setting \({\vec \Delta _i} = {\vec \Delta ^{\prime}_i} = 0\) and pi = p′i. The scheme we describe here for laser phase noise can be extended in a straight-forward way to include optical bench motion noise, which we address in the last part of this section.
The data combinations, when only the laser phase noise is considered, consist of the six suitably delayed data streams (inter-spacecraft), the delays being integer multiples of the light travel times between spacecraft, which can be conveniently expressed in terms of polynomials in the three delay operators \({{\mathcal D}_1},{{\mathcal D}_2},{{\mathcal D}_3}\). The laser noise cancellation condition puts three constraints on the six polynomials of the delay operators corresponding to the six data streams. The problem, therefore, consists of finding six-tuples of polynomials which satisfy the laser noise cancellation constraints. These polynomial tuples form a moduleFootnote 2 called the module of syzygies. There exist standard methods for obtaining the module, by which we mean methods for obtaining the generators of the module so that the linear combinations of the generators generate the entire module. The procedure first consists of obtaining a Gröbner basis for the ideal generated by the coefficients appearing in the constraints. This ideal is in the polynomial ring in the variables \({{\mathcal D}_1},{{\mathcal D}_2},{{\mathcal D}_3}\) over the domain of rational numbers (or integers if one gets rid of the denominators). To obtain the Gröbner basis for the ideal, one may use the Buchberger algorithm or use an application such as Mathematica [65]. From the Gröbner basis there is a standard way to obtain a generating set for the required module. This procedure has been described in the literature [3, 29]. We thus obtain seven generators for the module. However, the method does not guarantee a minimal set and we find that a generating set of 4 polynomial six-tuples suffice to generate the required module. Alternatively, we can obtain generating sets by using the software Macaulay 2.
The importance of obtaining more data combinations is evident: They provide the necessary redundancy — different data combinations produce different transfer functions for GWs and the system noises so specific data combinations could be optimal for given astrophysical source parameters in the context of maximizing SNR, detection probability, improving parameter estimates, etc.
4.1 Cancellation of laser phase noise
We now only have six data streams si and s′i, where i = 1, 2, 3. These can be regarded as 3 component vectors s and s′, respectively. The six data streams with terms containing only the laser frequency noise are
and their cyclic permutations.
Note that we have intentionally excluded from the data additional phase fluctuations due to the GW signal, and noises such as the optical-path noise, proof-mass noise, etc. Since our immediate goal is to cancel the laser frequency noise we have only kept the relevant terms. Combining the streams for canceling the laser frequency noise will introduce transfer functions for the other noises and the GW signal. This is important and will be discussed subsequently in the article.
The goal of the analysis is to add suitably delayed beams together so that the laser frequency noise terms add up to zero. This amounts to seeking data combinations that cancel the laser frequency noise. In the notation/formalism that we have invoked, the delay is obtained by applying the operators \({{\mathcal D}_k}\). to the beams si and s′i. A delay of k1L1 + k2L2 + k3L3 is represented by the operator \({\mathcal D}_1^{{k_1}}{\mathcal D}_2^{k2}{\mathcal D}_3^{{k_3}}\) acting on the data, where k1, k2, and k3 are integers. In general, a polynomial in \({{\mathcal D}_k}\), which is a polynomial in three variables, applied to, say, s1 combines the same data stream s1(t) with different time-delays of the form k1L1 + k2L2 + k3L3. This notation conveniently rephrases the problem. One must find six polynomials say \({q_i}({{\mathcal D}_1},{{\mathcal D}_2},{{\mathcal D}_3}),{q^{\prime}_i}({{\mathcal D}_1},{{\mathcal D}_2},{{\mathcal D}_3}),\;i = 1,2,3\) such that
The zero on the right-hand side of the above equation signifies zero laser phase noise.
It is useful to express Eq. (16) in matrix form. This allows us to obtain a matrix operator equation whose solutions are q and q′, where qi and q′i are written as column vectors. We can similarly express si, s′i, pi as column vectors s, s′, p, respectively. In matrix form Eq. (16) becomes
where D is a 3 × 3 matrix given by
The exponent ‘T’ represents the transpose of the matrix. Eq. (17) becomes
where we have taken care to put p on the right-hand side of the operators. Since the above equation must be satisfied for an arbitrary vector p, we obtain a matrix equation for the polynomials (q, q′):
Note that since the \({{\mathcal D}_k}\). commute, the order in writing these operators is unimportant. In mathematical terms, the polynomials form a commutative ring.
4.2 Cancellation of laser phase noise in the unequal-arm interferometer
The use of commutative algebra is very conveniently illustrated with the help of the simpler example of the unequal-arm interferometer. Here there are only two arms instead of three as we have for LISA, and the mathematics is much simpler and so it easy to see both physically and mathematically how commutative algebra can be applied to this problem of laser phase noise cancellation. The procedure is well known for the unequal-arm interferometer, but here we will describe the same method but in terms of the delay operators that we have introduced.
Let ϕ(t) denote the laser phase noise entering the laser cavity as shown in Figure 5. Consider this light ϕ(t) making a round trip around arm 1 whose length we take to be L1. If we interfere this phase with the incoming light we get the phase ϕ1(t), where
The second expression we have written in terms of the delay operators. This makes the procedure transparent as we shall see. We can do the same for the arm 2 to get another phase ϕ2(t), where
Clearly, if L1 ≠ L2, then the difference in phase ϕ2(t) − ϕ1(t) is not zero and the laser phase noise does not cancel out. However, if one further delays the phases ϕ1(t) and ϕ2() and constructs the following combination,
then the laser phase noise does cancel out. We have already encountered this combination at the end of Section 2. It was first proposed by Tinto and Armstrong in [53].
Schematic diagram of the unequal-arm Michelson interferometer. The beam shown corresponds to the term \(({\mathcal D}_2^2 - 1)({\mathcal D}_1^2 - 1)\phi (t)\) in X(t) which is first sent around arm 1 followed by arm 2. The second beam (not shown) is first sent around arm 2 and then through arm 1. The difference in these two beams constitutes X(t).
The cancellation of laser frequency noise becomes obvious from the operator algebra in the following way. In the operator notation,
From this one immediately sees that just the commutativity of the operators has been used to cancel the laser phase noise. The basic idea was to compute the lowest common multiple (L.C.M.) of the polynomials \({\mathcal D}_1^2 - 1\) and \({\mathcal D}_2^2 - 1\) (in this case the L.C.M. is just the product, because the polynomials are relatively prime) and use this fact to construct X(t) in which the laser phase noise is canceled. The operation is shown physically in Figure 5.
The notions of commutativity of polynomials, L.C.M., etc. belong to the field of commutative algebra. In fact we will be using the notion of a Groöbner basis which is in a sense the generalization of the notion of the greatest common divisor (gcd). Since LISA has three spacecraft and six inter-spacecraft beams, the problem of the unequal-arm interferometer only gets technically more complex; in principle the problem is the same as in this simpler case. Thus, the simple operations which were performed here to obtain a laser noise free combination X(t) are not sufficient and more sophisticated methods need to be adopted from the field of commutative algebra. We address this problem in the forthcoming text.
4.3 The module of syzygies
Equation (21) has non-trivial solutions. Several solutions have been exhibited in [2, 15]. We merely mention these solutions here; in the forthcoming text we will discuss them in detail. The solution ζ is given by \(- {{\rm{q}}^{\rm{T}}} = {{\rm{q^{\prime}}}^T} = ({{\mathcal D}_1},{{\mathcal D}_2},{{\mathcal D}_3})\). The solution α is described by \({{\rm{q}}^T} = - (1,{{\mathcal D}_3},{{\mathcal D}_1},{{\mathcal D}_3})\) and \({{\rm{q^{\prime}}}^T} = (1,{{\mathcal D}_1},{{\mathcal D}_2},{{\mathcal D}_2})\). The solutions β and γ are obtained from α by cyclically permuting the indices of \({{\mathcal D}_k},{\rm{q}}\) and q′. These solutions are important, because they consist of polynomials with lowest possible degrees and thus are simple. Other solutions containing higher degree polynomials can be generated conveniently from these solutions. Since the system of equations is linear, linear combinations of these solutions are also solutions to Eq. (21).
However, it is important to realize that we do not have a vector space here. Three independent constraints on a six-tuple do not produce a space which is necessarily generated by three basis elements. This conclusion would follow if the solutions formed a vector space but they do not. The polynomial six-tuple q, q′ can be multiplied by polynomials in \({{\mathcal D}_1},{{\mathcal D}_2},{{\mathcal D}_3}\) (scalars) which do not form a field. Thus, the inverse in general does not exist within the ring of polynomials. We, therefore, have a module over the ring of polynomials in the three variables \({{\mathcal D}_1},{{\mathcal D}_2},{{\mathcal D}_3}\). First we present the general methodology for obtaining the solutions to Eq. (21) and then apply it to Eq. (21).
There are three linear constraints on the polynomials given by Eq. (21). Since the equations are linear, the solutions space is a submodule of the module of six-tuples of polynomials. The module of six-tuples is a free module, i.e., it has six basis elements that not only generate the module but are linearly independent. A natural choice of the basis is fm = (0, …, 1, …, 0) with 1 in the m-th place and 0 everywhere else; m runs from 1 to 6. The definitions of generation (spanning) and linear independence are the same as that for vector spaces. A free module is essentially like a vector space. But our interest lies in its submodule which need not be free and need not have just three generators as it would seem if we were dealing with vector spaces.
The problem at hand is of finding the generators of this submodule, i.e., any element of the submodule should be expressible as a linear combination of the generating set. In this way the generators are capable of spanning the full submodule or generating the submodule. In order to achieve our goal, we rewrite Eq. (21) explicitly component-wise:
The first step is to use Gaussian elimination to obtain q1 and q2 in terms of q3, q′1, q′2, q′3,
and then substitute these values in the third equation to obtain a linear implicit relation between q3, q′1, q′2, q′3. We then have:
Obtaining solutions to Eq. (28) amounts to solving the problem since the remaining polynomials q1, q2 have been expressed in terms of q3, q′1, q′2, q′3 in Eq. (27). Note that we cannot carry on the Gaussian elimination process any further, because none of the polynomial coefficients appearing in Eq. (28) have an inverse in the ring.
We will assume that the polynomials have rational coefficients, i.e., the coefficients belong to \({\mathcal Q}\), the field of the rational numbers. The set of polynomials form a ring — the polynomial ring in three variables, which we denote by \({\mathcal R} = {\mathcal Q}[{{\mathcal D}_1},{{\mathcal D}_2},{{\mathcal D}_3}]\). The polynomial vector \(({q_3},{q^{\prime}_1},{q^{\prime}_2},{q^{\prime}_3})\;\;\in \;{{\mathcal R}^4}\). The set of solutions to Eq. (28) is just the kernel of the homomorphism \(\varphi \;:{{\mathcal R}^4}\; \rightarrow {\mathcal R}\), where the polynomial vector (q3, q′1, q′2, q′3) is mapped to the polynomial \((1 - {{\mathcal D}_1}{{\mathcal D}_2}{{\mathcal D}_3}){q_3}\; + ({{\mathcal D}_1}{{\mathcal D}_3} - {{\mathcal D}_2}){q^{\prime}_1} + {{\mathcal D}_1}(1 - {\mathcal D}_3^2){q^{\prime}_2}\; + (1 - {\mathcal D}_1^2){q^{\prime}_3}\). Thus, the solution space ker φ is a submodule of \({{\mathcal R}^4}\). It is called the module of syzygies. The generators of this module can be obtained from standard methods available in the literature. We briefly outline the method given in the books by Becker et al. [3], and Kreuzer and Robbiano [29] below. The details have been included in Appendix A.
4.4 Gröbner basis
The first step is to obtain the Gröbner basis for the ideal \({\mathcal U}\) generated by the coefficients in Eq. (28):
The ideal \({\mathcal U}\) consists of linear combinations of the form ∑viui where vi, i = 1,…, 4 are polynomials in the ring \({\mathcal R}\). There can be several sets of generators for \({\mathcal U}\). A Gröbner basis is a set of generators which is ‘small’ in a specific sense.
There are several ways to look at the theory of Gröbner basis. One way is the following: Suppose we are given polynomials g1, g2, …, gm in one variable over say \({\mathcal Q}\) and we would like to know whether another polynomial f belongs to the ideal generated by the g’s. A good way to decide the issue would be to first compute the gcd g of g1, g2, …, gm and check whether f is a multiple of g. One can achieve this by doing the long division of f by g and checking whether the remainder is zero. All this is possible because \({\mathcal Q}[x]\) is a Euclidean domain and also a principle ideal domain (PID) wherein any ideal is generated by a single element. Therefore we have essentially just one polynomial — the gcd — which generates the ideal generated by g1, g2, …, gm. The ring of integers or the ring of polynomials in one variable over any field are examples of PIDs whose ideals are generated by single elements. However, when we consider more general rings (not PIDs) like the one we are dealing with here, we do not have a single gcd but a set of several polynomials which generates an ideal in general. A Gröbner basis of an ideal can be thought of as a generalization of the gcd. In the univariate case, the Gröbner basis reduces to the gcd.
Gröbner basis theory generalizes these ideas to multivariate polynomials which are neither Euclidean rings nor PIDs. Since there is in general not a single generator for an ideal, Gröbner basis theory comes up with the idea of dividing a polynomial with a set of polynomials, the set of generators of the ideal, so that by successive divisions by the polynomials in this generating set of the given polynomial, the remainder becomes zero. Clearly, every generating set of polynomials need not possess this property. Those special generating sets that do possess this property (and they exist!) are called Gröbner bases. In order for a division to be carried out in a sensible manner, an order must be put on the ring of polynomials, so that the final remainder after every division is strictly smaller than each of the divisors in the generating set. A natural order exists on the ring of integers or on the polynomial ring \({\mathcal Q}(x)\); the degree of the polynomial decides the order in \({\mathcal Q}(x)\). However, even for polynomials in two variables there is no natural order a priori (is x2 + y greater or smaller than x + y2?). But one can, by hand as it were, put an order on such a ring by saying x ≫ y, where ≫ is an order, called the lexicographical order. We follow this type of order, \({{\mathcal D}_1} \gg {{\mathcal D}_2} \gg {{\mathcal D}_3}\) and ordering polynomials by considering their highest degree terms. It is possible to put different orderings on a given ring which then produce different Gröbner bases. Clearly, a Gröbner basis must have ‘small’ elements so that division is possible and every element of the ideal when divided by the Gröbner basis elements leaves zero remainder, i.e., every element modulo the Gröbner basis reduces to zero.
In the literature, there exists a well-known algorithm called the Buchberger algorithm, which may be used to obtain the Gröbner basis for a given set of polynomials in the ring. So a Gröbner basis of \({\mathcal U}\) can be obtained from the generators ui given in Eq. (29) using this algorithm. It is essentially again a generalization of the usual long division that we perform on univariate polynomials. More conveniently, we prefer to use the well known application Mathematica. Mathematica yields a 3-element Gröbner basis \({\mathcal G}\) for \({\mathcal U}\):
One can easily check that all the ui of Eq. (29) are linear combinations of the polynomials in \({\mathcal G}\) and hence \({\mathcal G}\) generates \({\mathcal U}\). One also observes that the elements look ‘small’ in the order mentioned above. However, one can satisfy oneself that \({\mathcal G}\) is a Gröbner basis by using the standard methods available in the literature. One method consists of computing the S-polynomials (see Appendix A) for all the pairs of the Gröbner basis elements and checking whether these reduce to zero modulo \({\mathcal G}\).
This Gröbner basis of the ideal \({\mathcal U}\) is then used to obtain the generators for the module of syzygies. Note that although the Gröbner basis depends on the order we choose among the \({{\mathcal D}_k}\), the module itself is independent of the order [3].
4.5 Generating set for the module of syzygies
The generating set for the module is obtained by further following the procedure in the literature [3, 29]. The details are given in Appendix A, specifically for our case. We obtain seven generators for the module. These generators do not form a minimal set and there are relations between them; in fact this method does not guarantee a minimum set of generators. These generators can be expressed as linear combinations of α, β, γ, ζ and also in terms of X(1), X(2), X(3), X(4) given below in Eq. (31). The importance in obtaining the seven generators is that the standard theorems guarantee that these seven generators do in fact generate the required module. Therefore, from this proven set of generators we can check whether a particular set is in fact a generating set. We present several generating sets below.
Alternatively, we may use a software package called Macaulay 2 which directly calculates the generators given the Eqs. (26). Using Macaulay 2, we obtain six generators. Again, Macaulay’s algorithm does not yield a minimal set; we can express the last two generators in terms of the first four. Below we list this smaller set of four generators in the order X = (q1, q2, q3, q′1, q′2, q′3):
Note that the last three generators are just X(2) = ζ, X(3) = α, X(4) = β. An extra generator X(1) is needed to generate all the solutions.
Another set of generators which may be useful for further work is a Gröbner basis of a module. The concept of a Gröbner basis of an ideal can be extended to that of a Gröbner basis of a submodule of (K[x1, x2, …, xn])m where K is a field, since a module over the polynomial ring can be considered as generalization of an ideal in a polynomial ring. Just as in the case of an ideal, a Gröbner basis for a module is a generating set with special properties. For the module under consideration we obtain a Gröbner basis using Macaulay 2:
Note that in this Gröbner basis G(1) = ζ = X(2), G(2) = X(1), G(3) = β = X(4), G(4) = α = X(3). Only G(5) is the new generator.
Another set of generators are just α, β, γ, and ζ. This can be checked using Macaulay 2, or one can relate α, β, γ, and ζ to the generators X(A), A = 1, 2, 3, 4, by polynomial matrices. In Appendix B, we express the seven generators we obtained following the literature, in terms of α, β, γ, and ζ. Also we express α, β, γ, and ζ in terms of X(A). This proves that all these sets generate the required module of syzygies.
The question now arises as to which set of generators we should choose which facilitates further analysis. The analysis is simplified if we choose a smaller number of generators. Also we would prefer low degree polynomials to appear in the generators so as to avoid cancellation of leading terms in the polynomials. By these two criteria we may choose X(A) or α, β, γ, ζ. However, α, β, γ, ζ possess the additional property that this set is left invariant under a cyclic permutation of indices 1, 2, 3. It is found that this set is more convenient to use because of this symmetry.
4.6 Canceling optical bench motion noise
There are now twelve Doppler data streams which have to be combined in an appropriate manner in order to cancel the noise from the laser as well as from the motion of the optical benches. As in the previous case of canceling laser phase noise, here too, we keep the relevant terms only, namely those terms containing laser phase noise and optical bench motion noise. We then have the following expressions for the four data streams on spacecraft 1:
The other eight data streams on spacecraft 2 and 3 are obtained by cyclic permutations of the indices in the above equations. In order to simplify the derivation of the expressions canceling the optical bench noises, we note that by subtracting Eq. (36) from Eq. (35), we can rewriting the resulting expression (and those obtained from it by permutation of the spacecraft indices) in the following form:
where ϕ′1, ϕ1 are defined as
The importance in defining these combinations is that the expressions for the data streams si, s′i simplify into the following form:
If we now combine the si, s′i, and zi in the following way,
we have just reduced the problem of canceling of six laser and six optical bench noises to the equivalent problem of removing the three random processes ϕ1, ϕ2, and ϕ3 from the six linear combinations ηi, η′i of the one-way measurements si, s′i, and zi. By comparing the equations above to Eq. (16) for the simpler configuration with only three lasers, analyzed in the previous Sections 4.1 to 4.4, we see that they are identical in form.
4.7 Physical interpretation of the TDI combinations
It is important to notice that the four interferometric combinations (α, β, γ, ζ), which can be used as a basis for generating the entire TDI space, are actually synthesized Sagnac interferometers. This can be seen by rewriting the expression for α, for instance, in the following form,
and noticing that the first square bracket on the right-hand side of Eq. (43) contains a combination of one-way measurements describing a light beam propagating clockwise around the array, while the other terms in the second square-bracket give the equivalent of another beam propagating counter-clockwise around the constellation.
Contrary to α, β, and γ, ζ can not be visualized as the difference (or interference) of two synthesized beams. However, it should still be regarded as a Sagnac combination since there exists a time-delay relationship between it and α, β, and γ [2]:
As a consequence of the time-structure of this relationship, has been called the symmetrized Sagnac combination.
By using the four generators, it is possible to construct several other interferometric combinations, such as the unequal-arm Michelson (X, Y, Z), the Beacons (P, Q, R), the Monitors (E, F, G), and the Relays (U, V, W). Contrary to the Sagnac combinations, these only use four of the six data combinations ηi, η′i. For this reason they have obvious utility in the event of selected subsystem failures [15].
These observables can be written in terms of the Sagnac observables (α, β, γ, ζ) in the following way,
as it is easy to verify by substituting the expressions for the Sagnac combinations into the above equations. Their physical interpretations are schematically shown in Figure 6.
In the case of the combination X, in particular, by writing it in the following form [2],
one can notice (as pointed out in [49] and [45]) that this combination can be visualized as the difference of two sums of phase measurements, each corresponding to a specific light path from a laser onboard spacecraft 1 having phase noise ϕ1. The first square-bracket term in Eq. (46) represents a synthesized light-beam transmitted from spacecraft 1 and made to bounce once at spacecraft 2 and 3, respectively. The second square-bracket term instead corresponds to another beam also originating from the same laser, experiencing the same overall delay as the first beam, but bouncing off spacecraft 3 first and then spacecraft 2. When they are recombined they will cancel the laser phase fluctuations exactly, having both experienced the same total delay (assuming stationary spacecraft). The X combinations should therefore be regarded as the response of a zero-area Sagnac interferometer.
5 Time-Delay Interferometry with Moving Spacecraft
The rotational motion of the LISA array results in a difference of the light travel times in the two directions around a Sagnac circuit [44, 7]. Two time delays along each arm must be used, say L′i and Li for clockwise or counter-clockwise propagation as they enter in any of the TDI combinations. Furthermore, since Li and L′i not only differ from one another but can be time dependent (they “flex”), it was shown that the “first generation” TDI combinations do not completely cancel the laser phase noise (at least with present laser stability requirements), which can enter at a level above the secondary noises. For LISA, and assuming \({\dot L_i} \simeq \;10{\rm{m/s}}\) [21], the estimated magnitude of the remaining frequency fluctuations from the laser can be about 30 times larger than the level set by the secondary noise sources in the center of the frequency band. In order to solve this potential problem, it has been shown that there exist new TDI combinations that are immune to first order shearing (flexing, or constant rate of change of delay times). These combinations can be derived by using the time-delay operators formalism introduced in the previous Section 4, although one has to keep in mind that now these operators no longer commute [58].
In order to derive the new, “flex-free” TDI combinations we will start by taking specific combinations of the one-way data entering in each of the expressions derived in the previous Section 4. Note, however, that now the expressions for the η-measurements assume the following form
where the ϕi, i = 1, 2, 3 measurements are as given in Eq. (38).
The new TDI combinations are chosen in such a way so as to retain only one of the three noises ϕi, i = 1, 2, 3, if possible. In this way we can then implement an iterative procedure based on the use of these basic combinations and of time-delay operators, to cancel the laser noises after dropping terms that are quadratic in \(\dot L/c\) or linear in the accelerations. This iterative time-delay method, to first order in the velocity, is illustrated abstractly as follows. Given a function of time Ψ = Ψ(t), time delay by Li is now denoted either with the standard comma notation [2] or by applying the delay operator \({{\mathcal D}_i}\) introduced in the previous Section 4,
We then impose a second time delay Li(t):
A third time delay Lk(t) gives
and so on, recursively; each delay generates a first-order correction proportional to its rate of change times the sum of all delays coming after it in the subscripts. Commas have now been replaced with semicolons [45], to remind us that we consider moving arrays. When the sum of these corrections to the terms of a data combination vanishes, the combination is called flex-free.
Also, note that each delay operator \({{\mathcal D}_i}\) has a unique inverse \(D_i^{- 1}\), whose expression can be derived by requiring that \(D_i^{- 1}{{\mathcal D}_i} = I\), and neglecting quadratic and higher order velocity terms. Its action on a time series Ψ(t) is
Note that this is not like an advance operator one might expect, since it advances not by Li(t) but rather Li(t + Li).
5.1 The unequal-arm Michelson
The unequal-arm Michelson combination relies on the four measurements η1, η1′, η2′, and η3. Note that the two combinations η1 + η2′,3, η1′ + η3,2′ represent the two synthesized two-way data measured onboard spacecraft 1, and can be written in the following form (see Eqs. (47), (48), and (49) for deriving the following synthesized two-way measurements)
where is the identity operator. Since in the stationary case any pairs of these operators commute, i.e., \({{\mathcal D}_i}{{\mathcal D}_{{j^\prime}}} - {{\mathcal D}_{{j^\prime}}}{{\mathcal D}_i} = 0\), from Eqs. (54) and (55) it is easy to derive the following expression for the unequal-arm interferometric combination X which eliminates ϕ1:
If, on the other hand, the time-delays depend on time, the expression of the unequal-arm Michelson combination above no longer cancels ϕ1. In order to derive the new expression for the unequal-arm interferometer that accounts for “flexing”, let us first consider the following two combinations of the one-way measurements entering into the X observable given in Eq. (56):
Using Eqs. (57) and (58), we can use the delay technique again to finally derive the following expression for the new unequal-arm Michelson combination X1 that accounts for the flexing effect:
As usual, X2 and X3 are obtained by cyclic permutation of the spacecraft indices. This expression is readily shown to be laser-noise-free to first order of spacecraft separation velocities \({\dot L_i}\): it is “flex-free”.
5.2 The Sagnac combinations
In the above Section 5.1, we have used the same symbol X for the unequal-arm Michelson combination for both the rotating (i.e., constant delay times) and stationary cases. This emphasizes that, for this TDI combination (and, as we will see below, also for all the combinations including only four links) the forms of the equations do not change going from systems at rest to the rotating case. One needs only distinguish between the time-of-flight variations in the clockwise and counter-clockwise senses (primed and unprimed delays).
In the case of the Sagnac variables (α, β, γ, ζ), however, this is not the case as it is easy to understand on simple physical grounds. In the case of α for instance, light originating from spacecraft 1 is simultaneously sent around the array on clockwise and counter-clockwise loops, and the two returning beams are then recombined. If the array is rotating, the two beams experience a different delay (the Sagnac effect), preventing the noise ϕ1 from canceling in the α combination.
In order to find the solution to this problem let us first rewrite α in such a way to explicitly emphasize what it does: attempts to remove the same fluctuations affecting two beams that have been made to propagated clockwise and counter-clockwise around the array,
where we have accounted for clockwise and counter-clockwise light delays. It is straight-forward to verify that this combination no longer cancels the laser and optical bench noises. If, however, we expand the two terms inside the square-brackets on the right-hand side of Eq. (60) we find that they are equal to
If we now apply our iterative scheme to the combinations given in Eq. (62) we finally get the expression for the Sagnac combination α1 that is unaffected by laser noise in presence of rotation,
If the delay-times are also time-dependent, we find that the residual laser noise remaining into the combination α1 is actually equal to
Fortunately, although first order in the relative velocities, the residual is small, as it involves the difference of the clockwise and counter-clockwise rates of change of the propagation delays on the same circuit. For LISA, the remaining laser phase noises in αi, i = 1, 2, 3, are several orders of magnitude below the secondary noises.
In the case of ζ, however, the rotation of the array breaks the symmetry and therefore its uniqueness. However, there still exist three generalized TDI laser-noise-free data combinations that have properties very similar to ζ, and which can be used for the same scientific purposes [54]. These combinations, which we call (ζ1, ζ2, ζ3), can be derived by applying again our time-delay operator approach.
Let us consider the following combination of the ηi, ηi′ measurements, each being delayed only once [2]:
where we have used the commutativity property of the delay operators in order to cancel the ϕ2 and ϕ3 terms. Since both sides of the two equations above contain only the ϕ1 noise, ζ1 is found by the following expression:
If the light-times in the arms are equal in the clockwise and counter-clockwise senses (e.g., no rotation) there is no distinction between primed and unprimed delay times. In this case, ζ1 is related to our original symmetric Sagnac ζ by ζ1 = ζ,23 − ζ,1. Thusm for the LISA case (arm length difference < 1%), the SNR of ζ1 will be the same as the SNR of ζ.
If the delay-times also change with time, the perfect cancellation of the laser noises is no longer achieved in the (ζ1, ζ2, ζ3) combinations. However, it has been shown in [58] that the magnitude of the residual laser noises in these combinations are significantly smaller than the LISA secondary system noises, making their effects entirely negligible.
The expressions for the Monitor, Beacon, and Relay combinations, accounting for the rotation and flexing of the LISA array, have been derived in the literature [58] by applying the time-delay iterative procedure highlighted in this section. The interested reader is referred to that paper for details.
5.3 Algebraic approach to second-generation TDI
In this subsection we present a mathematical formulation of the “second-generation” TDI, which generalizes the one presented in Section 4 for stationary LISA. Although a full solution as in the case of stationary LISA seems difficult to obtain, significant progress can be made.
There is, however, a case in between the 1st and 2nd generation TDI, called modified first-generation TDI, in which only the Sagnac effect is considered [7, 44]. In this case the up-down links are unequal while the delay-times remain constant. The mathematical formulation of Section 4 can be extended in a straight-forward way where now the six time-delays \({{\mathcal D}_i}\) and \({{\mathcal D}_{{i^\prime}}}\) must be taken into account. The polynomial ring still remains commutative but it is now in six variables. The corresponding module of syzygies can be constructed over this larger polynomial ring [41].
When the arms are allowed to flex, that is, the operators themselves are functions of time, the operators no longer commute. One must then resort to non-commutative algebra. We outline the procedure below. Since lot of the discussion has been covered in the previous subsections we just describe the algebraic formulation. The equation Eq. (26) generalizes in two ways: (1) we need to consider now six operators \({{\mathcal D}_i}\) and \({{\mathcal D}_{{i^\prime}}}\), and (2) we need to take into account the non-commutativity of the operators — the order of the operators is important. Accordingly Eq. (26) generalizes to,
Eliminating q1 and q2 from the three Eqs. (68) while respecting the order of the variables we get:
The polynomial ring \({\mathcal Q}({{\mathcal D}_i},{{\mathcal D}_{{i^\prime}}}) \equiv {\mathcal K}\), is non-commutative, of polynomials in the six variables \({{\mathcal D}_i},{{\mathcal D}_{{i^\prime}}}\) and coefficients in the rational field \({\mathcal Q}\). The polynomial vectors (qi, q′i) satisfying the above equations form a left module over \({\mathcal K}\). A left module means that one can multiply a solution (qi, q′i) from the left by any polynomial in \({\mathcal K}\), then it is also a solution to the Eqs. (68) and, therefore, in the module — the module of noise-free TDI observables. For details see [9].
When the operators do not commute, the algebraic problem is far more complex. If we follow on the lines of the commutative case, the first step would be to find a Gröbner basis for the ideal generated by the coefficients appearing in Eq. (69), namely, the set of polynomials \(\{1 - {{\mathcal D}_2}{{\mathcal D}_3}{{\mathcal D}_1},{{\mathcal D}_{{2^\prime}}} - {{\mathcal D}_3}{{\mathcal D}_1},({{\mathcal D}_{{3^\prime}}}{{\mathcal D}_3} - 1){{\mathcal D}_1},{{\mathcal D}_{{1^\prime}}}{{\mathcal D}_1} - 1\} \). Although we may be able to apply non-commutative Gröbner basis methods, the general solution seems quite difficult. However, simplifications are possible because of the inherent symmetries in the problem and so the ring \({\mathcal K}\) can be quotiented by a certain ideal, simplifying the algebraic problem. One then needs to deal with a ‘smaller’ ring, which may be easier to deal with. We describe below how this can achieved with the help of certain commutators.
In general, a commutator of two operators X, Y is defined as the operator [X, Y] = XY − YX. In our situation X and Y are strings of operators built up of the operators \({D_1},{D_2},{D_3},{D_{{1^\prime}}},{D_{{2^\prime}}},{D_{{3^\prime}}}\). For example, in the Sagnac combination the following commutator [12] occurs:
Here X = D1 D2 D3 and Y = D1′ D2′ D3′. This commutator leads to the residual noise term given in Eq. (64) and which happens to be small. In the context of the reasonably optimized model of LISA say given in [12], the residual noise term is small. For this model, we have \(\ddot L \sim {10^{- 6}}{\rm{m/}}{{\rm{s}}^2}\) and thus, even if one considers say 20 successive optical paths, that is, about Δt ∼ 330 s of light travel time, \(\Delta {t^2}\ddot L \sim 0.1\;{\rm{m}}\). This is well below few meters and thus can be neglected in the residual laser noise computation. Moreover, \({\dot L^2}\) terms (and higher order) can be dropped since they are of the order of ≲ 10−15 (they come with a factor 1/c2), which is much smaller than 1 part in 108, which is the level at which the laser frequency noise must be canceled. Thus, we keep terms only to the first degree in \(\dot L\) and also neglect higher time derivative terms in L.
The result for the Sagnac combination can be generalized. In order to simplify notation we write xk or ym for the time-delay operators, where k, m = 1, 2, …, n and n ≥ 2, that is, xk or ym are any of the operators D1, D2, D3, D1′, D2′, D3′. Then a commutator is:
Up to the order of approximation we are working in we compute the effect of the commutator on the phase ϕ(t):
Note that the LHS acts on ϕ(t), while the right-hand side multiplies \(\dot \phi \) at an appropriately delayed time. For the Sagnac combination this is readily seen from Eq. (64). Also the notation on the RHS is obvious: if for some k, we have, \({x_k} = {{\mathcal D}_{{2^\prime}}}\) say, then \({L_{{x_k}}} = {L\prime_2}\) and so on; the same holds for ym for a given m. From this equation it immediately follows that if the operators y1, y2, …, yn are a permutation of the operators x1, x2, …, xn, then the commutator,
up to the order we are working in. We can understand this by the following argument. If y1 … yn is a permutation of x1 … xn then both polynomials trace the same links, except that the nodes (spacecraft) of the links are taken in different orders. If the armlengths were constant, the path-lengths would be identical and the commutator would be zero. But here, by neglecting \(\ddot L\) terms and those of higher orders, we have effectively assumed that \({\dot L_s}\) are constant, so the increments also cancel out, resulting in a vanishing commutator.
These vanishing commutators (in the approximation we are working in) can be used to simplify the algebra. We first construct the ideal \({\mathcal U}\) generated by the commutators such as those given by Eq. (73). Then we quotient the ring \({\mathcal K}\) by \({\mathcal U}\), thereby constructing a smaller ring \({\mathcal K}/{\mathcal U} \equiv \bar {\mathcal K}\). This ring is smaller because it has fewer distinct terms in a polynomial. Although, this reduces the complexity of the problem, a full solution to the TDI problem is still lacking.
In the following Section 5.4, we will consider the case where we have only two arms of LISA in operation, that is one arm is nonfunctional. The algebraic problem simplifies considerably and it turns out to be tractable.
5.4 Solutions with one arm nonfunctional
We must envisage the possibility that not all optical links of LISA can be operating at all times for various reasons like technical failure for instance or even the operating costs. An analysis covering the scientific capabilities achievable by LISA in the eventuality of loosing one and two links has been discussed in [62]. Here we obtain the TDI combinations when one entire arm becomes dysfunctional. See [11] for a full discussion. The results of this section are directly usable by the eLISA/NGO mission.
We arbitrarily choose the non-functional arm to be the one connecting S/C 2 and S/C 3. This means from our labeling that the polynomials are now restricted to only the four operators \({{\mathcal D}_2},{{\mathcal D}_{{2^\prime}}},{{\mathcal D}_3},{{\mathcal D}_{{3^\prime}}}\) and we can set the polynomials q2 = q′3 = 0. This simplifies the Eqs. (68) considerably because the last two equations reduce to \(q_2^\prime = {q_1}{{\mathcal D}_3}\) and \({q_3} = q_1^\prime{{\mathcal D}_{{2^\prime}}}\). Substituting these in the first equation gives just one equation:
If we can solve this equation for q1, q′1 then the full polynomial vector can be obtained because \(q_2^\prime = {q_1}{{\mathcal D}_3}\) and \({q_3} = q_1^\prime{{\mathcal D}_{{2^\prime}}}\). It is clear that solutions are of the Michelson type. Also notice that the coefficients of this equation has the operators \(a = {{\mathcal D}_3}{{\mathcal D}_{{3^\prime}}}\) and \(b = {{\mathcal D}_{{2^\prime}}}{{\mathcal D}_2}\) occurring in them. So the solutions q1, q′1 too will be in terms of a and b only. Physically, the operators a and b correspond to round trips.
One solution has already been given in the literature [1, 61]. This solution in terms of a, b is:
Writing,
we get for Eq. (75), Δ = [ba, ab], which is a commutator that vanishes since ab is a permutation of ba. Thus, it is an element of \({\mathcal U}\) and Eq. (75) is a solution (over the quotient ring).
What we would like to emphasize is that there are more solutions of this type — in fact there are infinite number of such solutions. The solutions are based on vanishing of commutators. In [11] such commutators are enumerated and for each such commutator there is a corresponding solution. Further an algorithm is given to construct such solutions.
We briefly mention some results given in [11]. We start with the solutions q1, q′1 of Eq. (75). Note that these are of degree 3 in a and b. The commutator corresponding to this solution is Δ = [ba, ab] = ba2b − ab2a and is of degree 4. There is only one such commutator at degree 4 and therefore one solution. The next higher degree solutions are found when the commutators have degree 8. The solutions q1, q′1 are of degree 7. There are three such commutators at degree 8. We list the solutions and the commutators below. One solution is:
whose commutator is:
The second solution is:
whose commutator is Δ = [b2 a2, a2 a2].
The third solution corresponds to the commutator [baba, abab]. This solution is given by:
Higher degree solutions can be constructed. An iterative algorithm has been described in [11] for this purpose. The degrees of the commutators are in multiples of 4. If we call the degree of the commutators as 4 where n = 1, 2, …, then the solutions q1, q′1 are of degree 4n − 1. The cases mentioned above, correspond to n = 1 and n = 2. The general formula for the number of commutators of degree 4n is 2n−1Cn−1. So at n = 3 we have 10 commutators and so as many solutions q1, q′1 of degree 11.
These are the degrees of polynomials of q1, q′1 in the operators a, b. But for the full polynomial vector, which has q′2 and q3, we need to go over to the operators expressed in terms of \({{\mathcal D}_i},{{\mathcal D}_{{i^\prime}}}\). Then the degree of each of the q1, q′1 is doubled to 8n − 2, while q′2 and q3 are each of degree 8n − 1. Thus, for a general value of, the solution contains polynomials of maximum degree 8n − 1 in the time-delay operators.
From the mathematical point of view there is an infinite family of solutions. Note that no claim is made on exhaustive listing of solutions. However the family of solutions is sufficiently rich, because we can form linear combinations of these solutions and they also are solutions.
From the physical point of view, since terms in \(\ddot L\) and \({\dot L^2}\) and higher orders have been neglected, a limit on the degree of the polynomial solutions arises. That is up to certain degree of the polynomials, we can safely assume the commutators to vanish. But as the degree of the polynomials increases it is not possible to neglect these higher order terms any longer and then such a limit becomes important. The limit is essentially set by \(\ddot L\). We now investigate this limit and make a very rough estimate of it. As mentioned earlier, the LISA model in [12] gives \(\ddot L \sim {10^{- 6}}{\rm{m/}}{{\rm{s}}^2}\). From \(\ddot L\) we compute the error in L, namely, \(\Delta L \sim {1 \over 2}\Delta {t^2}\ddot L\). If we allow the error to be no more than say 10 meters, then we find Δt ∼ 4500 s. Since each time-delay is about 16.7 s for LISA, the number of successive time-delays is about 270. This is the maximum degree of the polynomials. This means one can go up to n ≲ 30. If we set the limit more stringently at ΔL ∼ 1 m, then the highest degree of the polynomial reduces to about 80, which means one can go up to n = 10. Thus, there are a large number of TDI observables available to do the physics.
Some remarks are in order:
-
A geometric combinatorial approach was adopted in [61] where several solutions were presented. Our approach is algebraic where the operations are algebraic operations on strings of operators. The algebraic approach has the advantage of easy manipulation of data streams, although some geometrical insight could be at a premium.
-
Another important aspect is the GW response of such TDI observables. The GW response to a TDI observable may be calculated in the simplest way by assuming equal arms (the possible differences in lengths would be sensitive to frequencies outside the LISA bandwidth). This leads in the Fourier domain to polynomials in the same phase factor from which the signal to noise ratio can be found. A comprehensive and generic treatment of the responses of second-generation TDI observables can be found in [30].
6 Optimal LISA Sensitivity
All the above interferometric combinations have been shown to individually have rather different sensitivities [15], as a consequence of their different responses to gravitational radiation and system noises. Since LISA has the capability of simultaneously observing a gravitational-wave signal with many different interferometric combinations (all having different antenna patterns and noises), we should no longer regard LISA as a single detector system but rather as an array of gravitational-wave detectors working in coincidence. This suggests that the LISA sensitivity could be improved by optimally combining elements of the TDI space.
Before proceeding with this idea, however, let us consider again the so-called “second-generation” TDI Sagnac observables: (α1, α2, α3). The expressions of the gravitational-wave signal and the secondary noise sources entering into α1 will in general be different from those entering into α, the corresponding Sagnac observable derived under the assumption of a stationary LISA array [2, 15]. However, the other remaining, secondary noises in LISA are so much smaller, and the rotation and systematic velocities in LISA are so intrinsically small, that index permutation may still be done for them [58]. It is therefore easy to derive the following relationship between the signal and secondary noises in α1, and those entering into the stationary TDI combination α [45, 58],
where Li, i = 1, 2, 3, are the unequal-arm lengths of the stationary LISA array. Equation (81) implies that any data analysis procedure and algorithm that will be implemented for the second-generation TDI combinations can actually be derived by considering the corresponding “first-generation” TDI combinations. For this reason, from now on we will focus our attention on the gravitational-wave responses of the first-generation TDI observables (α, β, γ, ζ).
As a consequence of these considerations, we can still regard (α, β, γ, ζ) as the generators of the TDI space, and write the most general expression for an element of the TDI space, η(f), as a linear combination of the Fourier transforms of the four generators \((\tilde \alpha, \tilde \beta, \tilde \gamma, \tilde \zeta)\),
where the \(\{{a_i}(f,\vec \lambda)\} _{i = 1}^4\) are arbitrary complex functions of the Fourier frequency f, and of a vector \(\vec \lambda \) containing parameters characterizing the gravitational-wave signal (source location in the sky, waveform parameters, etc.) and the noises affecting the four responses (noise levels, their correlations, etc.). For a given choice of the four functions \(\{{a_i}\} _{i = 1,}^4\eta \) η gives an element of the functional space of interferometric combinations generated by (α, β, γ, ζ). Our goal is therefore to identify, for a given gravitational-wave signal, the four functions \(\{{a_i}\} _{i = 1}^4\) that maximize the signal-to-noise ratio \({\rm{SNR}}_\eta ^2\) of the combination η,
In Eq. (83) the subscripts s and n refer to the signal and the noise parts of \((\tilde \alpha, \tilde \beta, \tilde \gamma, \tilde \zeta)\), respectively, the angle brackets represent noise ensemble averages, and the interval of integration (f1, fu) corresponds to the frequency band accessible by LISA.
Before proceeding with the maximization of the \({\rm{SNR}}_\eta ^2\) we may notice from Eq. (44) that the Fourier transform of the totally symmetric Sagnac combination, \(\tilde \zeta \), multiplied by the transfer function \(1 - {e^{2\pi if({L_1} + {L_2} + L3)}}\) can be written as a linear combination of the Fourier transforms of the remaining three generators \((\tilde \alpha, \tilde \beta, \tilde \gamma)\). Since the signal-to-noise ratio of η and \((1 - {e^{2\pi if({L_1} + {L_2} + {L_3})}})\eta \) are equal, we may conclude that the optimization of the signal-to-noise ratio of can be performed only on the three observables α, β, γ. This implies the following redefined expression for \({\rm{SNR}}_\eta ^2\):
The \({\rm{SNR}}_\eta ^2\) can be regarded as a functional over the space of the three complex functions \(\{{a_i}\} _{i = 1}^3\), and the particular set of complex functions that extremize it can of course be derived by solving the associated set of Euler-Lagrange equations.
In order to make the derivation of the optimal SNR easier, let us first denote by x(s) and x(n) the two vectors of the signals \(({\tilde \alpha _{\rm{s}}},{\tilde \beta _{\rm{s}}},{\tilde \gamma _{\rm{s}}})\) and the noises \(({\tilde \alpha _{\rm{n}}},{\tilde \beta _{\rm{n}}},{\tilde \gamma _{\rm{n}}})\), respectively. Let us also define a to be the vector of the three functions \(\{{a_i}\} _{i = 1}^3\), and denote with C the Hermitian, non-singular, correlation matrix of the vector random process xn,
If we finally define (A)ij to be the components of the Hermitian matrix \({\rm{x}}_i^{({\rm{s}})}{\rm{x}}_j^{({\rm{s}}) \ast}\), we can rewrite \({\rm{SNR}}_\eta ^2\) in the following form,
where we have adopted the usual convention of summation over repeated indices. Since the noise correlation matrix C is non-singular, and the integrand is positive definite or null, the stationary values of the signal-to-noise ratio will be attained at the stationary values of the integrand, which are given by solving the following set of equations (and their complex conjugated expressions):
After taking the partial derivatives, Eq. (87) can be rewritten in the following form,
which tells us that the stationary values of the signal-to-noise ratio of η are equal to the eigenvalues of the the matrix C−1 · A. The result in Eq. (87) is well known in the theory of quadratic forms, and it is called Rayleigh’s principle [36, 42].
In order now to identify the eigenvalues of the matrix C−1 · A, we first notice that the 3 × 3 matrix A has rank 1. This implies that the matrix C−1 · A has also rank 1, as it is easy to verify. Therefore two of its three eigenvalues are equal to zero, while the remaining non-zero eigenvalue represents the solution we are looking for.
The analytic expression of the third eigenvalue can be obtained by using the property that the trace of the 3 × 3 matrix C−1 · A is equal to the sum of its three eigenvalues, and in our case to the eigenvalue we are looking for. From these considerations we derive the following expression for the optimized signal-to-noise ratio \({\rm{SNR}}_{\eta \;{\rm{opt}}}^2\):
We can summarize the results derived in this section, which are given by Eqs. (84) and (89), in the following way:
-
1.
Among all possible interferometric combinations LISA will be able to synthesize with its four generators α, β, γ, ζ, the particular combination giving maximum signal-to-noise ratio can be obtained by using only three of them, namely (α, β, γ).
-
2.
The expression of the optimal signal-to-noise ratio given by Eq. (89) implies that LISA should be regarded as a network of three interferometer detectors of gravitational radiation (of responses (α, β, γ)) working in coincidence [20, 40].
6.1 General application
As an application of Eq. (89), here we calculate the sensitivity that LISA can reach when observing sinusoidal signals uniformly distributed on the celestial sphere and of random polarization. In order to calculate the optimal signal-to-noise ratio we will also need to use a specific expression for the noise correlation matrix C. As a simplification, we will assume the LISA arm lengths to be equal to their nominal value L = 16.67 s, the optical-path noises to be equal and uncorrelated to each other, and finally the noises due to the proof-mass noises to be also equal, uncorrelated to each other and to the optical-path noises. Under these assumptions the correlation matrix becomes real, its three diagonal elements are equal, and all the off-diagonal terms are equal to each other, as it is easy to verify by direct calculation [15]. The noise correlation matrix C is therefore uniquely identified by two real functions Sα and Sαβ in the following way:
The expression of the optimal signal-to-noise ratio assumes a rather simple form if we diagonalize this correlation matrix by properly “choosing a new basis”. There exists an orthogonal transformation of the generators \((\tilde \alpha, \tilde \beta, \tilde \gamma)\), which will transform the optimal signal-to-noise ratio into the sum of the signal-to-noise ratios of the “transformed” three interferometric combinations. The expressions of the three eigenvalues \(\{{\mu _i}\} _{i = 1}^3\) (which are real) of the noise correlation matrix C can easily be found by using the algebraic manipulator Mathematica, and they are equal to
Note that two of the three real eigenvalues, (μ1, μ2), are equal. This implies that the eigenvector associated to μ3 is orthogonal to the two-dimensional space generated by the eigenvalue μ1, while any chosen pair of eigenvectors corresponding to μ1 will not necessarily be orthogonal. This inconvenience can be avoided by choosing an arbitrary set of vectors in this two-dimensional space, and by ortho-normalizing them. After some simple algebra, we have derived the following three ortho-normalized eigenvectors:
Equation (92) implies the following three linear combinations of the generators \((\tilde \alpha, \tilde \beta, \tilde \gamma)\):
where A, E, and T are italicized to indicate that these are “orthogonal modes”. Although the expressions for the modes A and E depend on our particular choice for the two eigenvectors (v1, v2), it is clear from our earlier considerations that the value of the optimal signal-to-noise ratio is unaffected by such a choice. From Eq. (93) it is also easy to verify that the noise correlation matrix of these three combinations is diagonal, and that its non-zero elements are indeed equal to the eigenvalues given in Eq. (91).
In order to calculate the sensitivity corresponding to the expression of the optimal signal-to-noise ratio, we have proceeded similarly to what was done in [2, 15], and described in more detail in [56]. We assume an equal-arm LISA (L = 16.67 s), and take the one-sided spectra of proof mass and aggregate optical-path-noises (on a single link), expressed as fractional frequency fluctuation spectra, to be \(S_y^{{\rm{proof}}\,{\rm{mass}}} = 2.5 \times {10^{- 48}}{[f/1\,{\rm{Hz}}]^{- 2}}\,{\rm{H}}{{\rm{z}}^{- 1}}\) and \(S_y^{{\rm{optical}}\,{\rm{path}}} = 1.8 \times {10^{- 37}}{[f/1\,{\rm{Hz}}]^2}\,{\rm{H}}{{\rm{z}}^{- 1}}\), respectively (see [15, 5]). We also assume that aggregate optical path noise has the same transfer function as shot noise.
The optimum SNR is the square root of the sum of the squares of the SNRs of the three “orthogonal modes” (A, E, T). To compare with previous sensitivity curves of a single LISA Michelson interferometer, we construct the SNRs as a function of Fourier frequency for sinusoidal waves from sources uniformly distributed on the celestial sphere. To produce the SNR of each of the (A, E, T) modes we need the gravitational-wave response and the noise response as a function of Fourier frequency. We build up the gravitational-wave responses of the three modes (A, E, T) from the gravitational-wave responses of (α, β, γ). For 7000 Fourier frequencies in the ∼ 10−4 Hz to ∼ 1 Hz LISA band, we produce the Fourier transforms of the gravitational-wave response of (α, β, γ) from the formulas in [2, 56]. The averaging over source directions (uniformly distributed on the celestial sphere) and polarization states (uniformly distributed on the Poincaré sphere) is performed via a Monte Carlo method. From the Fourier transforms of the (α, β, γ) responses at each frequency, we construct the Fourier transforms of (A, E, T). We then square and average to compute the mean-squared responses of (A, E, T) at that frequency from 104 realizations of (source position, polarization state) pairs.
We adopt the following terminology: We refer to a single element of the module as a data combination, while a function of the elements of the module, such as taking the maximum over several data combinations in the module or squaring and adding data combinations belonging to the module, is called as an observable. The important point to note is that the laser frequency noise is also suppressed for the observable although it may not be an element of the module.
The noise spectra of (A, E, T) are determined from the raw spectra of proof-mass and optical-path noises, and the transfer functions of these noises to (A, E, T). Using the transfer functions given in [15], the resulting spectra are equal to
Let the amplitude of the sinusoidal gravitational wave be h. The SNR for, e.g., A, SNRA, at each frequency f is equal to h times the ratio of the root-mean-squared gravitational-wave response at that frequency divided by \(\sqrt {{S_A}(f)B} \), where B is the bandwidth conventionally taken to be equal to 1 cycle per year. Finally, if we take the reciprocal of SNRA/h and multiply it by 5 to get the conventional SNR = 5 sensitivity criterion, we obtain the sensitivity curve for this combination, which can then be compared against the corresponding sensitivity curve for the equal-arm Michelson interferometer.
In Figure 7 we show the sensitivity curve for the LISA equal-arm Michelson response (SNR = 5) as a function of the Fourier frequency, and the sensitivity curve from the optimum weighting of the data described above: \(5h/\sqrt {{\rm{SNR}}_A^2 + {\rm{SNR}}_E^2 + {\rm{SNR}}_T^2} \). The SNRs were computed for a bandwidth of 1 cycle/year. Note that at frequencies where the LISA Michelson combination has best sensitivity, the improvement in signal-to-noise ratio provided by the optimal observable is slightly larger than \(\sqrt 2 \).
In Figure 8 we plot the ratio between the optimal SNR and the SNR of a single Michelson interferometer. In the long-wavelength limit, the SNR improvement is \(\sqrt 2 \). For Fourier frequencies greater than or about equal to 1/L, the SNR improvement is larger and varies with the frequency, showing an average value of about \(\sqrt 3 \). In particular, for bands of frequencies centered on integer multiples of 1/L, SNRT contributes strongly and the aggregate SNR in these bands can be greater than 2.
The optimal SNR divided by the SNR of a single Michelson interferometer, as a function of the Fourier frequency f. The sensitivity gain in the low-frequency band is equal to \(\sqrt 2 \), while it can get larger than 2 at selected frequencies in the high-frequency region of the accessible band. The integration time has been assumed to be one year, and the proof mass and optical path noise spectra are the nominal ones. See the main body of the paper for a quantitative discussion of this point.
In order to better understand the contribution from the three different combinations to the optimal combination of the three generators, in Figure 9 we plot the signal-to-noise ratios of (A, E, T) as well as the optimal signal-to-noise ratio. For an assumed h = 10−23, the SNRs of the three modes are plotted versus frequency. For the equal-arm case computed here, the SNRs of A and E are equal across the band. In the long wavelength region of the band, modes A and E have SNRs much greater than mode T, where its contribution to the total SNR is negligible. At higher frequencies, however, the T combination has SNR greater than or comparable to the other modes and can dominate the SNR improvement at selected frequencies. Some of these results have also been obtained in [40].
The SNRs of the three combinations (A, E, T) and their sum as a function of the Fourier frequency f. The SNRs of A and E are equal over the entire frequency band. The SNR of T is significantly smaller than the other two in the low part of the frequency band, while is comparable to (and at times larger than) the SNR of the other two in the high-frequency region. See text for a complete discussion.
6.2 Optimization of SNR for binaries with known direction but with unknown orientation of the orbital plane
Binaries are important sources for LISA and therefore the analysis of such sources is of major importance. One such class is of massive or super-massive binaries whose individual masses could range from 103M⊙ to 108M⊙ and which could be up to a few Gpc away. Another class of interest are known binaries within our own galaxy whose individual masses are of the order of a solar mass but are just at a distance of a few kpc or less. Here the focus will be on this latter class of binaries. It is assumed that the direction of the source is known, which is so for known binaries in our galaxy. However, even for such binaries, the inclination angle of the plane of the orbit of the binary is either poorly estimated or unknown. The optimization problem is now posed differently: The SNR is optimized after averaging over the polarizations of the binary signals, so the results obtained are optimal on the average, that is, the source is tracked with an observable which is optimal on the average [40]. For computing the average, a uniform distribution for the direction of the orbital angular momentum of the binary is assumed.
When the binary masses are of the order of a solar mass and the signal typically has a frequency of a few mHz, the GW frequency of the binary may be taken to be constant over the period of observation, which is typically taken to be of the order of an year. A complete calculation of the signal matrix and the optimization procedure of SNR is given in [39]. Here we briefly mention the main points and the final results.
A source fixed in the Solar System Barycentric reference frame in the direction (θB, ϕB) is considered. But as the LISA constellation moves along its heliocentric orbit, the apparent direction (θL, ϕL) of the source in the LISA reference frame (xL, yL, zL) changes with time. The LISA reference frame (xL, yL, zL) has been defined in [39] as follows: The origin lies at the center of the LISA triangle and the plane of LISA coincides with the (xL, yL) plane with spacecraft 2 lying on the xL axis. Figure (10) displays this apparent motion for a source lying in the ecliptic plane, that is with θB = 90° and ϕB = 0°. The source in the LISA reference frame describes a figure of 8. Optimizing the SNR amounts to tracking the source with an optimal observable as the source apparently moves in the LISA reference frame.
Since an average has been taken over the orientation of the orbital plane of the binary or equivalently over the polarizations, the signal matrix A is now of rank 2 instead of rank 1 as compared with the application in the previous Section 6.1. The mutually orthogonal data combinations A, E, T are convenient in carrying out the computations because in this case as well, they simultaneously diagonalize the signal and the noise covariance matrix. The optimization problem now reduces to an eigenvalue problem with the eigenvalues being the squares of the SNRs. There are two eigen-vectors which are labeled as \({\vec \upsilon _{+, \times}}\) belonging to two non-zero eigenvalues. The two SNRs are labelled as SNR+ and SNR×, corresponding to the two orthogonal (thus statistically independent) eigenvectors \({\vec \upsilon _{+, \times}}\). As was done in the previous Section 6.1 F the two SNRs can be squared and added to yield a network SNR, which is defined through the equation
The corresponding observable is called the network observable. The third eigenvalue is zero and the corresponding eigenvector orthogonal to \({\vec \upsilon _ +}\) and \({\vec \upsilon _ \times}\) gives zero signal.
The eigenvectors and the SNRs are functions of the apparent source direction parameters (θL, ϕL) in the LISA reference frame, which in turn are functions of time. The eigenvectors optimally track the source as it moves in the LISA reference frame. Assuming an observation period of an year, the SNRs are integrated over this period of time. The sensitivities are computed according to the procedure described in the previous Section 6.1. The results of these findings are displayed in Figure 11.
It shows the sensitivity curves of the following observables:
-
1.
The Michelson combination X (faint solid curve).
-
2.
The observable obtained by taking the maximum sensitivity among X, Y, and Z for each direction, where Y and Z are the Michelson observables corresponding to the remaining two pairs of arms of LISA [2]. This maximum is denoted by max[X, Y, Z] (dash-dotted curve) and is operationally given by switching the combinations X, Y, Z so that the best sensitivity is achieved.
-
3.
The eigen-combination \({\vec \upsilon _ +}\) which has the best sensitivity among all data combinations (dashed curve).
-
4.
The network observable (solid curve).
It is observed that the sensitivity over the band-width of LISA increases as one goes from Observable 1 to 4. Also it is seen that the max[X, Y, Z] does not do much better than X. This is because for the source direction chosen θB = 90°, X is reasonably well oriented and switching to Y and Z combinations does not improve the sensitivity significantly. However, the network and \({\vec \upsilon _ +}\) observables show significant improvement in sensitivity over both X and max[X, Y, Z]. This is the typical behavior and the sensitivity curves (except) do not show much variations for other source directions and the plots are similar. Also it may be fair to compare the optimal sensitivities with max[X, Y, Z] rather than X. This comparison of sensitivities is shown in Figure 12, where the network and the eigen-combinations \({\vec \upsilon _{+, \times}}\) are compared with max[X, Y, Z].
Defining
where the subscript a stands for network or +, ×, and SNRmax[X, Y, Z] is the SNR of the observable max[X, Y, Z], the ratios of sensitivities are plotted over the LISA band-width. The improvement in sensitivity for the network observable is about 34% at low frequencies and rises to nearly 90% at about 20 mHz, while at the same time the \({\vec \upsilon _ +}\) combination shows improvement of 12% at low frequencies rising to over 50% at about 20 mHz.
7 Experimental Aspects of TDI
It is clear that the suppression of the laser phase fluctuations by more than nine orders of magnitude with the use of TDI is a very challenging experimental task. It requires developing and building subsystems capable of unprecedented accuracy and precision levels, and test their end-to-end performance in a laboratory environment that naturally precludes the availability of 5 × 106 km delay lines! In what follows we will address some aspects related to the experimental implementation of TDI, and derive the performance specifications for the subsystems involved. We will not address, however, any of the experimental aspects related to the verification of TDI in a laboratory environment. For that, we refer the interested reader to de Vine et al. [8, 32], Spero et al. [48], and Mitryk et al. [33].
From simple physical grounds, it is easy to see that a successful implementation of TDI requires:
-
1.
accurate knowledge of the time shifts, L′i(t), Li(t) i = 1, 2, 3, to be applied to the heterodyne measurements si(t), s′i(t), τi(t), τ′i(t) i = 1, 2, 3;
-
2.
accurate synchronization among the three clocks onboard the three spacecraft as these are used for time-stamping the recorded heterodyne phase measurements;
-
3.
sampling time stability (i.e., clock stability) for successfully suppressing the laser noise to the desired level;
-
4.
an accurate reconstruction algorithm of the phase measurements corresponding to the required time delays as these in general will not be equal to integer multiples of the sampling time;
-
5.
a phase meter capable of a very large dynamic range in order to suppress the laser noise to the required level while still preserving the phase fluctuations induced by a gravitational-wave signal in the TDI combinations.
In the following subsections, we will quantitatively address the issues listed above, and provide the reader with a related list of references where more details can be found.
7.1 Time-delays accuracies
The TDI combinations described in the previous sections (whether of the first- or second-generation) rely on the assumption of knowing the time-delays with infinite accuracy to exactly cancel the laser noise. Since the six delays will in fact be known only within the accuracies δLi, δL′i i = 1, 2, 3, the cancellation of the laser frequency fluctuations in, for instance, the combinations (α, β, γ, ζ) will no longer be exact. In order to estimate the magnitude of the laser fluctuations remaining in these data sets, let us define \({\hat L_i}\;,{\hat L\prime_i}\;i = 1,2,3\) to be the estimated time-delays. They are related to the true delays Li, L′i i = 1, 2, 3, and the accuracies δLi, δL′i i = 1, 2, 3 through the following expressions
and similarly for the primed delays. In what follows we will limit our derivation of the time-delays accuracies to only the first-generation TDI combinations and treat the three common delays Li, i = 1, 2, 3 as constants equal to 16.7 light-seconds. We will also assume to know with infinite accuracies and precisions all the remaining physical quantities (listed at the beginning of Section 7) that are needed to successfully synthesize the TDI generators.
If we now substitute Eq. (98) into the expression for the TDI combination α, for instance, (Eq. (43)) and expand it to first order in δLi, it is easy to derive the following approximate expression for \(\hat \alpha (t)\), which now will show a non-zero contribution from the laser noises
where the symbol denotes time derivative. Time-delay interferometry can be considered effective if the magnitude of the remaining fluctuations from the lasers are much smaller than the fluctuations due to the remaining (proof mass and optical path) noises entering α(t). This requirement implies a limit in the accuracies of the measured delays.
Let us assume the laser phase fluctuations to be uncorrelated to each other, their one-sided power spectral densities to be equal, the three armlengths to differ by a few percent, and the three armlength accuracies also to be equal. By requiring the magnitude of the remaining laser noises to be smaller than the secondary noise sources, it is straightforward to derive, from Eq. (99) and the expressions for the noise spectrum of the α TDI combination given in [15], the following constraint on the common armlength accuracy ∣δLα∣
with similar inequalities also holding for β and γ. Here Sϕ, Sproof mass, Soptical path are the onesided power spectral densities of the relative frequency fluctuations of a stabilized laser, a single proof mass, and a single-link optical path respectively. If we take them to be equal to the following functions of the Fourier frequency f [53, 15]
(where f is in Hz), we find that the right-hand side of the inequality given by Eq. (100) reaches its minimum of about 30 meters at the Fourier frequency fmin = 1.0 × 10−4 Hz, over the assumed (10−4,1) Hz LISA band. This implies that, if the armlength knowledge ∣δLα∣ can be made much smaller than 30 meters, the magnitude of the residual laser noise affecting the α combination can be regarded as negligible over the entire frequency band. This reflects the fact that the armlength accuracy is a decreasing function of the frequency. For instance, at 10−3 Hz the armlength accuracy goes up by almost an order of magnitude to about 155 meters.
A perturbation analysis similar to the one described above can be performed for ζ, resulting into the following inequality for the required delay accuracy, ∣δLζ∣
Equation (104) implies a minimum of the function on the right-hand side equal to about 16 meters at the Fourier frequency fmin = 1.0 × 10−4 Hz, while at 10−3 Hz the armlength accuracy goes up to 154 meters.
Armlength accuracies at the centimeters level have already been demonstrated in the laboratory [16, 50, 64, 26], making us confident that the required level of time-delays accuracy will be available.
In relation to the accuracies derived above, it is interesting to calculate the time scales during which the armlengths will change by an amount equal to the accuracies themselves. This identifies the minimum time required before updating the armlength values in the TDI combinations.
It has been calculated by Folkner et al. [21] that the relative longitudinal speeds between the three pairs of spacecraft, during approximately the first year of the LISA mission, can be written in the following approximate form
where we have denoted with (1, 2), (1, 3), (2, 3) the three possible spacecraft pairs, \(V_{i,j}^{(0)}\) is a constant velocity, and Ti,j is the period for the pair (i, j). In reference [21] it has also been shown that the LISA trajectory can be selected in such a way that two of the three arms’ rates of change are essentially equal during the first year of the mission. Following reference [21], we will assume \(V_{1,2}^{(0)} = V_{1,3}^{(0)} \neq V_{2,3}^{(0)}\), with \(V_{1,2}^{(0)} = 1\;{\rm{m/s,}}\;V_{2,3}^{(0)} = 13\;{\rm{m/s,}}\;{T_{1,2}}\; = {T_{1,3}} \approx 4\) months, and \({T_{2,3}} \approx 1\) year. From Eq. (105) it is easy to derive the variation of each armlength, for example ΔL3(t), as a function of the time and the time scale δt during which it takes place
Equation (106) implies that a variation in armlength ΔL3 ≈ 10 m can take place during different time scales, depending on when during the mission this change takes place. For instance, if t ≪ T1,2 we find that the armlength L3 changes by more than its accuracy (≈ 10 m) after a time δt = 2.3 × 103 s. If however t ≃ T1,2/4, the armlength will change by the same amount after only δt ≃ 10 s instead. As this value is less than the one-way-light-time, one might argue that the measured time-delay will not represent well enough the delay that needs to be applied in the TDI combinations at that particular time.
One way to address this problem is to treat the delays in the TDI combinations as parameters to be determined by a non-linear least-squares procedure, in which the minimum of the minimizer is achieved at the correct delays since that the laser noise will exactly cancel there in the TDI combinations. Such a technique, which was named time-delay interferometric ranging (TDIR) [60], requires a starting point in the time-delays space in order to implement the minimization, and it will work quite effectively jointly with the ranging data available onboard.
7.2 Clocks synchronization
The effectiveness of the TDI data combinations requires the clocks onboard the three spacecraft to be synchronized. In what follows we will identify the minimum level of off-synchronization among the clocks that can be tolerated. In order to proceed with our analysis we will treat one of the three clocks (say the clock onboard spacecraft 1) as the master clock defining the time for LISA, while the other two to be synchronized to it.
The relativistic (Sagnac) time-delay effect due to the fact that the LISA trajectory is a combination of two rotations, each with a period of one year, will have to be accounted for in the synchronization procedure and, as has already been discussed earlier, will be accounted for within the second-generation formulation of TDI.
Here, for simplicity, we will analyze an idealized non-rotating constellation in order to get a sense of the required level of clocks synchronization. Let us denote by δt2, δt3, the time accuracies (time-offsets) for the clocks onboard spacecraft 2 and 3 respectively. If t is the time onboard spacecraft 1, then what is believed to be time t onboard spacecraft 2 and 3 is actually equal to the following times
If we now substitute Eqs. (107 and 108) into the TDI combination ζ, for instance, and expand it to first order in δti, i = 2, 3, it is easy to derive the following approximate expression for \(\hat \zeta (t)\), which shows the following non-zero contribution from the laser noises
By requiring again the magnitude of the remaining fluctuations from the lasers to be smaller than the fluctuations due to the other (secondary) noise sources affecting ζ(t), it is possible to derive an upper limit for the accuracies of the synchronization of the clocks. If we assume again the three laser phase fluctuations to be uncorrelated to each other, their one-sided power spectral densities to be equal, the three armlengths to differ by a few percent, and the two time-offsets’ magnitudes to be equal, by requiring the magnitude of the remaining laser noises to be smaller than the secondary noise sources it is easy to derive the following constraint on the time synchronization accuracy ∣δtζ∣
with Sϕ, Sproof mass, Soptical path again as given in Eqs. (101–103).
We find that the right-hand side of the inequality given by Eq. (110) reaches its minimum of about 47 nanoseconds at the Fourier frequency fmin = 1.0 × 10−4 Hz. This means that clocks synchronized at a level of accuracy significantly better than 47 nanoseconds will result into a residual laser noise that is much smaller than the secondary noise sources entering into the ζ combination.
An analysis similar to the one described above can be performed for the remaining generators (α, β, γ). For them we find that the corresponding inequality for the accuracy in the synchronization of the clocks is now equal to
with equal expressions holding also for β and γ. The function on the right-hand side of Eq. (111) has a minimum equal to 88 nanoseconds at the Fourier frequency fmin = 1.0 × 10−4 Hz. As for the armlength accuracies, also the timing accuracy requirements become less stringent at higher frequencies. At 10−3 Hz, for instance, the timing accuracy for ζ and α, β, γ go up to 446 and 500 ns respectively.
As a final note, a required clock synchronizations of about 40 ns derived in this section translates into a ranging accuracy of 12 meters, which has been experimentally shown to be easily achievable [16, 50, 64, 26].
7.3 Clocks timing jitter
The sampling times of all the measurements needed for synthesizing the TDI combinations will not be constant, due to the intrinsic timing jitters of the onboard measuring system. Among all the subsystems involved in the data measuring process, the onboard clock is expected to be the dominant source of time jitter in the sampled data. Presently existing space qualified clocks can achieve an Allan standard deviation of about 10−13 for integration times from 1 to 10 000 seconds. This timing stability translates into a time jitter of about 10−13 seconds over a period of 1 second. A perturbation analysis including the three sampling time jitters due to the three clocks shows that any laser phase fluctuations remaining in the four TDI generators will also be proportional to the sampling time jitters. Since the latter are approximately four orders of magnitude smaller than the armlength and clocks synchronization accuracies derived earlier, we conclude that the magnitude of laser noise residual into the TDI combinations due to the sampling time jitters is negligible.
7.4 Sampling reconstruction algorithm
The derivations of the time-delays and clocks synchronization accuracies highlighted earlier presumed the availability of the phase measurement samples at the required time-delays. Since this condition will not be true in general, as the time-delays used by the TDI combinations will not be equal to integer-multiples of the sampling time, with a sampling rate of, let us say, 10 Hz, the time delays could be off their correct values by a tenth of a second, way more than the 10 nanoseconds time-delays and clocks synchronization accuracies estimated above.
Earlier suggestions [27] for addressing this problem envisioned sampling the data at very-high rates (perhaps of the order of hundreds of MHz), so reducing the additional error to the estimated time-delays to a few nanoseconds. Although in principle such a solution would allow us to suppress the residual laser noise to the required level, it would create an insurmountable problem for transmitting the science data to the ground due to the limited space-to-ground data rates.
An alternate scheme for obtaining the phase measurement points needed by TDI [59] envisioned sampling the phase measurements at the required delayed times. This scheme naturally requires knowledge of the time-delays and synchronization of the clocks at the required accuracy levels during data acquisition. Although such a procedure could be feasible in principle, it would still leave open the possibility of irreversible corruption of the TDI combinations in the eventuality of performance degradation in the ranging and clock synchronization procedures.
Given that the data will need to be sampled at a rate of 10 Hz, an alternative options is to implement an interpolation scheme for reconstructing the required data points from the sampled measurements. An analysis [59] based on the implementation of the truncated Shannon [47] formula, however, showed that several months of data were required in order to reconstruct the phase samples at the estimated time-delays with a sufficiently high accuracy. This conclusion implied that several months (at the beginning and end) of the entire data records measured by LISA would be of no use, resulting into a significant mission science degradation.
Although the truncated Shannon formula was proved to be impracticable [59] for reconstructing phase samples at the required time-delays, it was then recognized that [46] a more efficient and accurate interpolation technique [31] could be adopted. In what follows, we provide a brief account of this data processing technique, which is known as “fractional-delay filtering” (FDF).
In order to understand how FDF works, let’s write the truncated Shannon formula for the delayed sample, yN(n − D), which we want to construct by filtering the sampled data y(n)
where, as usual, sinc(x) ≡ sin(x)/x, and N is an integer at which the Shannon formula has been truncated to. As pointed out in [46], although the truncated Shannon formula is optimal in the least-squares sense, the sinc-function that appears in it is far from being ideal in reconstructing the transfer function \({e^{2\pi ifD/{f_s}}}\), where fs is the sampling frequency. In fact, over the LISA observational band the sinc-function displays significant ringing, which can only be suppressed by taking N very large (as the error, ϵ, decays slowly as 1/N). It was estimated that, in order to achieve an ϵ < 10−8, an N ≥ 108 is needed.
If, however, we give up on the requirement of minimizing the error in the least-squares sense and replace it with a mini-max criterion error applied to the absolute value of the difference between the ideal transfer function (i.e., \({e^{2\pi ifD/{f_s}}}\)) and a modified sinc-function, we will be able to achieve a rapid convergence while suppressing the ringing effects associated with the sinc function.
One way to achieve this result is to modify the Shannon formula by multiplying the sinc-function by a window-function, W(j), in the following way
where W(j) smoothly decays to zero at j = ±N. In [46] several windows were tested, and the resulting values of N needed to accurately reconstruct the desired delayed samples were estimated, both on theoretical and numerically grounds. It was found that, with windows belonging to the family of Lagrange polynomials [46] a delayed sample could be reconstructed by using N ≃ 25 samples while achieving a mini-max error ϵ < 10−12 between the ideal transfer function \({e^{2\pi ifD/{f_s}}}\), and the kernel of the modified truncated Shannon formula.
7.5 Data digitization and bit-accuracy requirement
It has been shown [59] that the maximum of the ratio between the amplitudes of the laser and the secondary phase fluctuations occurs at the lower end of the LISA bandwidth (i.e., 0.1 mHz) and it is equal to about 1010. This corresponds to the minimum dynamic range for the phasemeters to correctly measure the laser fluctuations and the weaker (gravitational-wave) signals simultaneously. An additional safety factor of ≈ 10 should be sufficient to avoid saturation if the noises are well described by Gaussian statistics. In terms of requirements on the digital signal processing subsystem, this dynamic range implies that approximately 36 bits are needed when combining the signals in TDI, only to bridge the gap between laser frequency noise and the other noises and gravitational-wave signals. More bits might be necessary to provide enough information to efficiently filter the data when extracting weak gravitational-wave signals embedded into noise.
The phasemeters will be the onboard instrument that will perform the phase measurements containing the gravitational signals. They will also need to simultaneously measure the time-delays to be applied to the TDI combinations via ranging tones over-imposed on the laser beams exchanged by the spacecraft. And they will need to have the capability of simultaneously measure additional side-band tones that are required for the calibration of the onboard Ultra-Stable Oscillator used in the down-conversion of heterodyned carrier signal [57, 27].
Work toward the realization of a phasemeter capable of meeting these very stringent performance and operational requirements has aggressively been performed both in the United States and in Europe [43, 23, 22, 6, 63], and we refer the reader interested in the technical details associated with the development studies of such device to the above references and those therein.
8 Concluding Remarks
In this article we have summarized the use of TDI for canceling the laser phase noise from heterodyne phase measurements performed by a constellation of three spacecraft tracking each other along arms of unequal length. Underlying the TDI technique is the mathematical structure of the theory of Gröbner basis and the algebra of modules over polynomial rings. These methods have been motivated and illustrated with the simple example of an unequal-arm interferometer in order to give a physical insight of TDI. Here, these methods have been rigorously applied to the idealized case of a stationary interferometer such as the LISA mission. This allowed us to derive the generators of the module from which the entire TDI data set can be obtained; they can be extended in a straight-forward way to more than three spacecraft for possible future mission concepts. The stationary LISA case was used as a propaedeutical introduction to the physical motivation of TDI, and for further extending it to the realistic LISA configuration of free-falling spacecraft orbiting around the Sun. The TDI data combinations canceling laser phase noise in this general case are referred to as second-generation TDI, and they contain twice as many terms as their corresponding first-generation combinations valid for the stationary configuration.
As a data analysis application we have shown that it is possible to identify specific TDI combinations that will allow LISA to achieve optimal sensitivity to gravitational radiation [38, 40, 39]. The resulting improvement in sensitivity over that of an unequal-arm Michelson interferometer, in the case of monochromatic signals randomly distributed over the celestial sphere and of random polarization, is non-negligible. We have found this to be equal to a factor of \(\sqrt 2 \) in the low-part of the frequency band, and slightly more than \(\sqrt 3 \) in the high-part of the LISA band. The SNR for binaries whose location in the sky is known, but their polarization is not, can also be optimized, and the degree of improvement depends on the location of the source in the sky.
We also addressed several experimental aspects of TDI, and emphasized that it has already been successfully tested experimentally [8, 32, 48, 33].
As of the writing of this second edition of our living review article, it is very gratifying to see how much TDI has matured since the publishing of its first version. The purpose of this second edition review of TDI was to provide the basic mathematical tools and knowledge of the current experimental results needed for working on future TDI projects. We hope to have accomplished this goal, and that others will be stimulated to work in this fascinating field of research.
Notes
It should be noticed that the optical bench design shown in Figure 4 is one the earlier ones proposed for the LISA mission, and it represents one of the possible configurations for integrating the onboard drag-free system with the TDI measurements. Although other optical bench designs will result into different inter-proof-mass phase measurements, they can be accommodated within TDI [37].
A module is an Abelian group over a ring as contrasted with a vector space which is an Abelian group over a field. The scalars form a ring and just like in a vector space, scalar multiplication is defined. However, in a ring the multiplicative inverses do not exist in general for the elements, which makes all the difference!
References
Armstrong, J. W., “Low-Frequency Gravitational Wave Searches Using Spacecraft Doppler Tracking”, Living Rev. Relativity, 9, lrr-2006-1 (2006). [DOI], [ADS]. URL (accessed 25 February 2014): http://www.livingreviews.org/lrr-2006-1. (Cited on page 30.)
Armstrong, J. W., Estabrook, F. B. and Tinto, M., “Time-Delay Interferometry for Space-Based Gravitational Wave Searches”, Astrophys. J., 527, 814–826, (1999). [DOI], [ADS]. (Cited on pages 6, 7, 15, 19, 23, 24, 25, 27, 32, 35, and 39.)
Becker, T. and Weispfenning, V., Gröbner Bases: A Computational Approach to Commutative Algebra, Graduate Texts in Mathematics, 141, (Springer, Berlin; New York, 1993). (Cited on pages 7, 16, 20, 21, and 49.)
Bender, P. L. and Hils, D., “Confusion noise level due to galactic and extragalactic binaries”, Class. Quantum Grav., 14, 1439–1444, (1997). [DOI], [ADS]. (Cited on page 5.)
Bender, P. L. et al. (LISA Study Team), LISA. Laser Interferometer Space Antenna for the detection and observation of gravitational waves. An international project in the field of Fundamental Physics in Space. Pre-Phase A report, MPQ-233, (Max-Planck-Institut für Quantenoptik, Garching, 1998). Online version (accessed 6 July 2005): ftp://ftp.ipp-garching.mpg.de/pub/grav/lisa/pdd/. (Cited on pages 6, 9, and 35.)
Burnett, C. M., Development ofan Ultra-precise Digital Phasemeter for the LISA Gravitational Wave Detector, Master’s thesis, (Lulea University of Technology, Kiruna, Sweden, 2010). Online version (accessed 25 February 2014): http://pure.ltu.se/portal/files/32538169/LTU-EX-2011-32455311.pdf. (Cited on page 46.)
Cornish, N. J. and Hellings, R. W., “The effects of orbital motion on LISA time delay interferometry”, Class. Quantum Grav., 20, 4851–4860, (2003). [DOI]. (Cited on pages 8, 12, 13, 25, and 28.)
de Vine, G., Ware, B., McKenzie, K., Spero, R. E., Klipstein, W. M. and Shaddock, D. A., “Experimental Demonstration of Time-Delay Interferometry for the Laser Interferometer Space Antenna”, Phys. Rev. Lett., 104, 211103 (2010). [DOI], [ADS], [arXiv:1005.2176 [astro-ph.IM]]. (Cited on pages 8, 41, and 47.)
Dhurandhar, S. V., “Time-delay interferometry and the relativistic treatment of LISA optical links”, J. Phys.: Conf. Ser., 154, 012047 (2009). [DOI], [arXiv:0808.2696 [gr-qc]]. (Cited on pages 8 and 28.)
Dhurandhar, S. V., Rajesh Nayak, K. and Vinet, J.-Y., “Algebraic approach to time-delay data analysis for LISA”, Phys. Rev. D, 65, 102002 (2002). [DOI]. (Cited on pages 6 and 7.)
Dhurandhar, S. V., Rajesh Nayak, K. and Vinet, J.-Y., “Time Delay Interferometry for LISA with one arm dysfunctional”, Class. Quantum Grav., 27, 135013 (2010). [DOI], [arXiv:1001.4911 [gr-qc]]. (Cited on pages 8, 30, and 31.)
Dhurandhar, S. V., Vinet, J.-Y. and Rajesh Nayak, K., “General relativistic treatment of LISA optical links”, Class. Quantum Grav., 25, 245002 (2008). [DOI]. (Cited on pages 29 and 31.)
“eLISA”, project homepage, Max Planck Institute for Gravitational Physics (Albert Einstein Institute). URL (accessed 26 February 2014): https://www.elisascience.org/. (Cited on pages 5, 6, 8, and 9.)
Estabrook, F. and Wahlquist, H., “Response of Doppler spacecraft tracking to gravitational radiation”, Gen. Relativ. Gravit., 6, 439–447, (1975). [DOI], [ADS]. (Cited on page 6.)
Estabrook, F. B., Tinto, M. and Armstrong, J. W., “Time-delay analysis of LISA gravitational wave data: Elimination of spacecraft motion effects”, Phys. Rev. D, 62, 042002 (2000). [DOI], [ADS]. (Cited on pages 7, 8, 13, 14, 15, 19, 24, 32, 34, 35, and 42.)
Esteban, J. J., García, A. F., Barke, S., Peinado, A.M, Guzmán Cervantes, F., Bykov, I., Heinzel, G. and Danzmann, K., “Experimental demonstration of weak-light laser ranging and data communication for LISA”, Opt. Express, 19(17), 15937–15946 (2011). [DOI]. (Cited on pages 42 and 44.)
Faller, J. E. and Bender, P. L., “A possible laser gravitational wave experiment in space”, in Taylor, B. N. and Phillips, W. D., eds., Precision Measurement and Fundamental Constants II, Proceedings of the Second International Conference held at the National Bureau of Standards, Gaithersburg, MD, June 8–12, 1981, NBS Special Publication, 617, pp. 689–690, (U.S. Dept. of Commerce / National Bureau of Standards, Washington, DC, 1984). (Cited on pages 9 and 10.)
Faller, J. E., Bender, P. L., Hall, J. L., Hils, D., Stebbins, R. T. and Vincent, M. A., “An antenna for laser gravitational-wave observations in space”, Adv. Space Res., 9, 107–111, (1989). [DOI], [ADS]. COSPAR and IAU, 27th Plenary Meeting, 15th Symposium on Relativistic Gravitation, Espoo, Finland, July 18–29, 1988. (Cited on page 9.)
Faller, J. E., Bender, P. L., Hall, J. L., Hils, D. and Vincent, M. A., “Space antenna for gravitational wave astronomy”, in Longdon, N. and Melita, O., eds., Kilometric Optical Arrays in Space, Proceedings of the Colloquium held 23–25 October 1984, Cargèse, Corsica, France, ESA Conference Proceedings, SP-226, pp. 157–163, (ESA Publications Division, Noordwijk, 1985). (Cited on page 9.)
Finn, L. S., “Aperture synthesis for gravitational-wave data analysis: Deterministic sources”, Phys. Rev. D, 63, 102001 (2001). [DOI], [gr-qc/0010033]. (Cited on page 34.)
Folkner, W. M., Hechler, F., Sweetser, T. H., Vincent, M. A. and Bender, P. L., “LISA orbit selection and stability”, Class. Quantum Grav., 14, 1405–1410, (1997). [DOI]. (Cited on pages 25 and 43.)
Gerberding, O., Sheard, B., Bykov, I., Kullmann, J., Esteban Delgado, J. J., Danzmann, K. and Heinzel, G., “Phasemeter core for intersatellite laser heterodyne interferometry: modelling, simulations and experiments”, Class. Quantum Grav., 30, 235029 (2013). [DOI]. (Cited on page 46.)
Gerberding, O. et al., “Breadboard Model of the LISA Phasemeter”, in Auger, G., Binétruy, P. and Plagnol, E., eds., The 9th LISA Sympsium, Bibliothéque Nationale de France, Paris, 21–25 May 2012, ASP Conference Series, 467, pp. 271–275, (Astronomical Society of the Pacific, San Francisco, 2013). (Cited on page 46.)
Giampieri, G., Hellings, R. W., Tinto, M. and Faller, J. E., “Algorithms for unequal-arm Michelson interferometers”, Opt. Commun., 123, 669–678, (1996). [DOI]. (Cited on page 9.)
Gruning, P., Halloin, H., Prat, P., Baron, S., Brossard, J., Buy, C. and Petiteau, A., “Progress towards an electro-optical simulator for space based, long arms interferometers”, arXiv, e-print, (2013). [ADS], [arXiv:1309.1059 [gr-qc]]. (Cited on page 8.)
Heinzel, G., Esteban, J. J., Barke, S., Otto, M., Wang, Y., Garcia, A. F. and Danzmann, K., “Auxiliary functions of the LISA laser link: ranging, clock noise transfer and data communication”, Class. Quantum Grav., 28, 094008 (2011). [DOI], [ADS]. (Cited on pages 42 and 44.)
Hellings, R. W., “Elimination of clock jitter noise in spaceborne laser interferometers.”, Phys. Rev. D, 64, 022002 (2001). [DOI]. (Cited on pages 45 and 46.)
Jenkins, G. M. and Watts, D. G., Spectral Analysis and its applications, (Holden-Day, San Francisco, 1969). (Cited on page 10.)
Kreuzer, M. and Robbiano, L., Computational Commutative Algebra 1, (Springer, Berlin; New York, 2000). [Google Books]. (Cited on pages 7, 16, 20, and 21.)
Królak, A., Tinto, M. and Vallisneri, M., “Optimal filtering of the LISA data”, Phys. Rev. D, 70, 022003 (2004). [DOI], [arXiv:gr-qc/0401108 [gr-qc]]. Erratum ibid. 76, 069901 (2007). (Cited on page 31.)
Laakso, T. I., Välimäki, V., Karjalainen, M. and Laine, U. K., “Splitting the Unit Delay”, IEEE Signal Proc. Mag., 1(30), 30–60 (1996). [DOI]. (Cited on page 45.)
Miller, J., “Laboratory experiment shows that noise can be lessened for LISA”, Phys. Today, 63, 14–16, (2010). [DOI]. (Cited on pages 8, 41, and 47.)
Mitryk, S. J., Mueller, G. and Sanjuan, J., “Hardware-based demonstration of time-delay interferometry and TDI-ranging with spacecraft motion effects”, Phys. Rev. D, 86, 122006 (2012). [DOI], [ADS], [1205.1934 [astro-ph.IM]]. (Cited on pages 8, 41, and 47.)
Nelemans, G., Yungelson, L. R. and Portegies Zwart, S. F., “The gravitational wave signal from the Galactic disk population of binaries containing two compact objects”, Astron. Astrophys., 375, 890–898, (2001). [DOI], [ADS], [arXiv:astro-ph/0105221]. (Cited on page 5.)
“NGO: The New Gravitational Wave Observatory”, project homepage, European Space Agency. URL (accessed 26 February 2014): http://sci.esa.int/ngo/. (Cited on pages 5, 6, 8, and 9.)
Noble, B., Applied Linear Algebra, (Prentice-Hall, Englewood Cliffs, 1969). (Cited on page 33.)
Otto, M., Heinzel, G. and Danzmann, K., “TDI and clock noise removal for the split interferometry configuration of LISA”, Class. Quantum Grav., 29, 205003 (2012). [DOI], [ADS]. (Cited on page 14.)
Prince, T. A., Tinto, M., Larson, S. L. and Armstrong, J. W., “LISA optimal sensitivity”, Phys. Rev. D, 66, 122002 (2002). [DOI], [ADS], [arXiv:gr-qc/0209039]. (Cited on pages 8 and 47.)
Rajesh Nayak, K., Dhurandhar, S. V., Pai, A. and Vinet, J.-Y., “Optimizing the directional sensitivity of LISA”, Phys. Rev. D, 68, 122001 (2003). [DOI]. (Cited on pages 8, 38, and 47.)
Rajesh Nayak, K., Pai, A., Dhurandhar, S. V. and Vinet, J.-Y., “Improving the sensitivity of LISA”, Class. Quantum Grav., 20, 1217–1231, (2003). (Cited on pages 8, 34, 37, 38, and 47.)
Rajesh Nayak, K. and Vinet, J.-Y., “Algebraic Approach to Time-Delay Data Analysis: Orbiting case”, Class. Quantum Grav., 22, S437–S443, (2005). [DOI]. (Cited on pages 8 and 28.)
Selby, S. M., Standard of Mathematical Tables, (The Chemical Rubber Co., Cleveland, 1964). (Cited on page 33.)
Shaddock, D., Ware, B., Spero, R. E. and Klipstein, B., “Overview of the LISA Phasemeter”, in Merkowitz, S. M. and Livas, J. C., eds., Laser Interferometer Space Antenna: 6th International LISA Symposium, Greenbelt, MD, USA, 19–23 June 2006, AIP Conference Proceedings, 873, pp. 654–660, (American Institute of Physics, Melville, NY, 2006). [DOI], [ADS]. (Cited on page 46.)
Shaddock, D. A., “Operating LISA as a Sagnac interferometer”, Phys. Rev. D, 69, 022001 (2004). [DOI], [ADS]. (Cited on pages 8, 12, 25, and 28.)
Shaddock, D. A., Tinto, M., Estabrook, F. B. and Armstrong, J. W., “Data combinations accounting for LISA spacecraft motion”, Phys. Rev. D, 68, 061303 (2003). [DOI]. (Cited on pages 8, 11, 12, 13, 24, 25, and 32.)
Shaddock, D. A., Ware, B., Spero, R. E. and Vallisneri, M., “Postprocessed time-delay interferometry for LISA”, Phys. Rev. D, 70, 081101(R) (2004). [DOI]. (Cited on pages 45 and 46.)
Shannon, C. E., “Communication in the Presence of Noise”, Proc. IEEE, 86, 0018–9219–98 (1998). [DOI]. (Cited on page 45.)
Spero, R. et al., “Progress in interferometry for LISA at JPL”, Class. Quantum Grav., 28, 094007 (2011). [DOI], [arXiv:1102.0799 [physics.ins-det]]. (Cited on pages 8, 41, and 47.)
Summers, D., “Algorithm tradeoffs”, conference paper, (2003). Talk given at the 3rd progress meeting of the ESA funded LISA PMS Project. ESTEC, NL, February 2003. (Cited on page 24.)
Sutton, A., McKenzie, K., Ware, B. and Shaddock, D. A., “Laser ranging and communications for LISA”, Opt. Express, 18(20), 20759–20773 (2010). [DOI]. (Cited on pages 42 and 44.)
Tinto, M., “Spacecraft to spacecraft coherent laser tracking as a xylophone interferometer detector of gravitational radiation”, Phys. Rev. D, 58, 102001 (1998). [DOI], [ADS]. (Cited on pages 6 and 7.)
Tinto, M., “The Cassini Ka-band gravitational wave experiments”, Class. Quantum Grav., 19, 1767–1773, (2002). [DOI]. (Cited on page 6.)
Tinto, M. and Armstrong, J. W., “Cancellation of laser noise in an unequal-arm interferometer detector of gravitational radiation”, Phys. Rev. D, 59, 102003 (1999). [DOI]. (Cited on pages 6, 11, 18, and 42.)
Tinto, M., Armstrong, J. W. and Estabrook, F. B., “Discriminating a gravitational wave background from instrumental noise in the LISA detector”, Phys. Rev. D, 63, 021101(R) (2001). [DOI], [ADS]. (Cited on page 27.)
Tinto, M. and Estabrook, F. B., “Parallel beam interferometric detectors of gravitational waves”, Phys. Rev. D, 52, 1749–1754, (1995). [DOI]. (Cited on page 6.)
Tinto, M., Estabrook, F. B. and Armstrong, J. W., Time-Delay Interferometry and LISA’s Sensitivity to Sinusoidal Gravitational Waves, (JPL / Caltech, Pasadena, CA, 2002). Online version (accessed 1 November 2013): http://list.caltech.edu/doku.php?id=mission_documents. (Cited on page 35.)
Tinto, M., Estabrook, F. B. and Armstrong, J. W., “Time-delay interferometry for LISA”, Phys. Rev. D, 65, 082003 (2002). [DOI], [ADS]. (Cited on pages 6, 13, 14, and 46.)
Tinto, M., Estabrook, F. B. and Armstrong, J. W., “Time-delay interferometry with moving spacecraft arrays”, Phys. Rev. D, 69, 082001 (2004). [DOI]. (Cited on pages 8, 12, 13, 25, 28, and 32.)
Tinto, M., Shaddock, D. A., Sylvestre, J. and Armstrong, J. W., “Implementation of time-delay interferometry for LISA”, Phys. Rev. D, 67, 122003 (2003). [DOI]. (Cited on pages 45 and 46.)
Tinto, M., Vallisneri, M. and Armstrong, J. W., “Time-delay interferometric ranging for space-borne gravitational-wave detectors”, Phys. Rev. D, 71, 041101 (2005). [DOI]. (Cited on page 43.)
Vallisneri, M., “Geometric time delay interferometry”, Phys. Rev. D, 72, 042003 (2005). [DOI], [ADS], [arXiv:gr-qc/0504145 [gr-qc]]. (Cited on pages 30 and 31.)
Vallisneri, M., Crowder, J. and Tinto, M., “Sensitivity and parameter-estimation precision for alternate LISA configurations”, Class. Quantum Grav., 25, 065005 (2008). [DOI], [ADS], [arXiv:0710.4369]. (Cited on page 30.)
Wang, C., FPGA-based, 4-channel, High-speed Phasemeter for Heterodyne Interferometry, Master’s thesis, (University of Rochester, Rochester, NY, 2013). Online version (accessed 25 February 2014): http://www.me.rochester.edu/projects/jdellis-lab/files/2013_ChenWang_MS_Thesis.pdf. (Cited on page 46.)
Wang, Y., Heinzel, G. and Danzmann, K., “The first stage of LISA data processing: clock synchronization and arm-length determination via a hybrid-extended Kalman filter”, arXiv, e-print, (2014). [ADS], [arXiv:1402.6222 [gr-qc]]. (Cited on pages 42 and 44.)
Wolfram, S., “Wolfram Mathematica”, institutional homepage, Wolfram Research, Inc. URL (accessed 26 February 2014): http://www.wolfram.com/mathematica/. (Cited on page 16.)
Acknowledgement
S.V.D. acknowledges support from IFCPAR, Delhi, India under which the work was carried out in collaboration with J.-Y. Vinet. S.V.D. also thanks IUCAA for a visiting professorship during which this article was updated. This research was performed at the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
Author information
Authors and Affiliations
Corresponding author
Appendices
Generators of the Module of Syzygies
We require the 4-tuple solutions (q3, q′1, q′2, q′3) to the equation
where for convenience we have substituted \(x = {{\mathcal D}_1},y = {{\mathcal D}_2},z = {{\mathcal D}_3}.\;{q_3},\;q_1^\prime,\;q_2^\prime,\;q_3^\prime\) are polynomials in x, y, z with integral coefficients, i.e., in Z[x, y, z]
We now follow the procedure in the book by Becker et al. [3].
Consider the ideal in Z[x, y, z] (or \({\mathcal Q}[x,y,z]\) where \({\mathcal Q}\) denotes the field of rational numbers), formed by taking linear combinations of the coefficients in Eq. (114), f1 = 1 − xyz, f2 = xz − y, f3 = x(1 − z2), f4 = 1 − x2. A Gröbner basis for this ideal is
The above Gröbner basis is obtained using the function GroebnerBasis in Mathematica. One can check that both the fi, i = 1, 2, 3, 4, and gj, j = 1, 2, 3, generate the same ideal because we can express one generating set in terms of the other and vice-versa:
where d and c are 4 × 3 and 3 × 4 polynomial matrices, respectively, and are given by
The generators of the 4-tuple module are given by the set A ∪ B*, where A and B* are the sets described below:
A is the set of row vectors of the matrix I − d · c where the dot denotes the matrix product and I is the identity matrix, 4 × 4 in our case. Thus,
We thus first get four generators. The additional generators are obtained by computing the S-polynomials of the Gröbner basis \({\mathcal G}\). The S-polynomial of two polynomials g1, g2 is obtained by multiplying g1 and g2 by suitable terms and then adding, so that the highest terms cancel. For example in our case g1 = z2 − 1 and g2 = y2 − 1, and the highest terms are z2 for g1 and y2 for g2 Multiply g1 by y2 and g2 by z2 and subtract. Thus, the S-polynomial p12 of g1 and g2 is
Note that order is defined (x ≫ y ≫ z) and the y2z2 term cancels. For the Gröbner basis of 3 elements we get 3 S-polynomials p12, p13, p23. The pij must now be re-expressed in terms of the Gröbner basis \(\mathcal{G}\). This gives a 3 × 3 matrix b. The final step is to transform to four-tuples by multiplying b by the matrix c to obtain b* = b · c. The row vectors b*i, i = 1, 2, 3 of b* form the set B*:
Thus, we obtain three more generators, which gives us a total of seven generators of the required module of syzygies.
Conversion between Generating Sets
We list the three sets of generators and relations among them. We first list below α, β, γ, ζ:
We now express the ai and b*j in terms of α, β, γ, ζ:
Further, we also list below α, β, γ, ζ in terms of X(A):
This proves that since the ai, b*j generate the required module, the α, β, γ, ζ and X(A), A = 1, 2, 3, 4, also generate the same module.
The Gröbner basis is given in terms of the above generators as follows: G(1) = ζ, G(2) = X(1), G(3) = β, G(A) = α, and G(5) = α3.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Tinto, M., Dhurandhar, S.V. Time-Delay Interferometry. Living Rev. Relativ. 17, 6 (2014). https://doi.org/10.12942/lrr-2014-6
Accepted:
Published:
DOI: https://doi.org/10.12942/lrr-2014-6
Keywords
Article history
Latest
Time-delay interferometry- Published:
- 15 December 2020
- Received:
- 17 February 2020
- Accepted:
- 20 October 2020
DOI: https://doi.org/10.1007/s41114-020-00029-6
- Time-Delay Interferometry
- Published:
- 05 August 2014
- Accepted:
- 28 July 2014
DOI: https://doi.org/10.12942/lrr-2014-6
Original
Time-Delay Interferometry- Published:
- 15 July 2005
- Accepted:
- 16 May 2005
DOI: https://doi.org/10.12942/lrr-2005-4