Abstract
Magnetic activity similar to that of the Sun is observed on a variety of cool stars with external convection envelopes. Stellar rotation coupled with convective motions generate strong magnetic fields in the stellar interior and produce a multitude of magnetic phenomena including starspots in the photosphere, chromospheric plages, coronal loops, UV, X-ray, and radio emission and flares. Here I review the phenomenon of starspots on different types of cool stars, observational tools and diagnostic techniques for studying starspots as well as starspot properties including their temperatures, areas, magnetic field strengths, lifetimes, active latitudes and longitudes, etc. Evolution of starspots on various time scales allows us to investigate stellar differential rotation, activity cycles, and global magnetic fields. Together these constitute the basis for our understanding of stellar and solar dynamos and provide valuable constraints for theoretical models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The multitude of activity phenomena on the Sun are related to magnetic fields which are generated by cyclonic turbulence in the outer convection zone and penetrate the solar atmosphere forming sunspots, plages, network, etc. They further expand into the outer atmosphere and exhibit themselves as highly dynamic coronal loops. Thus, a detailed study of solar activity phenomena reveals the structure of underlying magnetic fields and provides valuable constraints for solar dynamo theory. These same activity phenomena are observed on cool stars with outer convection zones.
Studying magnetic activity on stars other than the Sun provides an opportunity for detailed tests of solar dynamo models. Using only solar observations limits the range of the global stellar parameters for such tests, while an extensive sample of stars of various activity levels provides key constraints for stellar and solar dynamo theory.
Stellar activity similar to that of the Sun was first discovered on red dwarfs, a fraction of which exhibit remarkable magnetic activity registered through observations of extremely strong optical flares (UV Cet-type stars). Periodic brightness variations were observed in binary systems of red dwarfs (BY Dra-type) as distortions of the light curves outside eclipses. Kron (1947) was seemingly the first who considered the hypothesis that spottedness of the stellar surface was causing these distortions. Later, light-curve variations due to starspots and other magnetic phenomena were discovered on various types of stars.
It was suggested by Skumanich (1972) that rotation plays a crucial role in the generation of stellar activity. This became evident later from the strong correlation of magnetic activity indicators with stellar rotational velocities and periods. Such relations have been reported between rotation and coronal emission (Pallavicini et al., 1981; Walter and Bowyer, 1981), chromospheric Ca ii and Hα emission (Vaughan et al., 1981; Middelkoop, 1981; Mekkaden, 1985), ultraviolet line fluxes (Vilhu, 1984; Simon and Fekel, 1987), and radio emission (Drake et al., 1989). It was found that cool stars with more rapid rotation show a higher level of magnetic activity. Such active stars are the best choice for testing and developing stellar dynamo theory. Among single stars these are pre-main-sequence stars (T Tau-type) and early-age main-sequence stars of solar type. Evolved binary components which are tidally locked at fast rotation by a close companion are also strongly magnetically active (RS CVn-type, BY Dra-type, W UMa-type, and Algol-like systems). Rapidly rotating single giants of FK Com-type, which are probably formed from coalesced binaries complete the selection of magnetically active stars. An overview of magnetic phenomena on such stars is given in Section 2.
Significant progress in observational tools and diagnostic techniques for studying starspots over the last two decades has advanced our understanding of the nature of stellar activity. Long-term traditional photometric observations reveal active region evolution and stellar activity cycles. Highresolution spectroscopy allows for studies of the structure of active regions and stellar differential rotation with the help of the Doppler imaging technique (Vogt et al., 1987; Rice et al., 1989; Piskunov et al., 1990; Collier Cameron, 1992; Jankov and Foing, 1992; Berdyugina, 1998; Rice and Strassmeier, 2000). Observations of molecular lines provide a unique opportunity for insight into spatially unresolved starspots (Berdyugina, 2002) and unambiguous measurements of starspot temperature (O’Neal et al., 1996). Spectropolarimetry reveals the distribution of magnetic fields on the stellar surface thanks to the Zeeman-Doppler imaging technique (Donati et al., 1997). Novel applications of (spectro-)interferometry, microlensing, asteroseismology, etc., broaden the arsenal of tools and techniques for studying starspots. These are reviewed in Sections 3 and 4.
Since the discovery of rotationally modulated brightness variations due to starspots, a large amount of data has been collected for different types of stars. Brightness and colour variations allow for determining temperature of starspots and their relative area. Doppler images reveal spot distribution which is different from that observed on the Sun. Polarimetric measurements of starspots help to investigate the nature of the underlying magnetic fields. Starspot properties, including their temperature, sizes, magnetic field strengths, lifetimes, and distribution over latitudes and longitudes are reviewed in Section 5.
Time-series observations over decades reveal stellar cycles similar to the 11-year sunspot cycle. On the other hand, persistent active longitudes and a new type of stellar cycle related to them (flip-flop cycle) have been first discovered on cool stars and later on the Sun (Berdyugina and Tuominen, 1998; Berdyugina and Usoskin, 2003). In binaries, orbital period variations suggest long-term changes of the magnetic field distribution in stellar interiors (Hall, 1991b; Rodonò et al., 1995; Lanza et al., 1998a). Such observations provide valuable constraints for stellar and solar dynamo models. An overview of stellar activity cycles and their implications for dynamo theory is given in Sections 6 and 7.
Previous short reviews on starspots and their role in understanding the stellar dynamo were given by Hall (1991a), Lanza and Rodonò (1999a), Berdyugina (2004) and Strassmeier (2005). Also, starspots were thoroughly discussed at the international workshop “Surface Inhomogeneities on Late-Type Stars” (1990, Armagh), IAU Symposium 175 “Stellar Surface Structures” (1995, Vienna) and the First Potsdam Thinkshop “Sunspots and Starspots” (2002, Potsdam). The present review covers main tendencies in starspot research for the last two decades.
2 The Phenomenon of Stellar Activity
2.1 Red dwarfs and BY Dra phenomenon
Red dwarfs are main-sequence stars with the mass range from 0.08 M⊙ to 0.5 M⊙. The lower mass limit is the critical mass for hydrogen burning in the central cores of stars with solar abundances, while the upper limit corresponds to the spectral class M0. The radii of the red dwarfs span from 0.2R⊙ to about 0.6 R⊙ while their effective temperatures are in the range of 2500 K–4000 K. Thus, red dwarf stars are cooler, smaller, and less massive than the Sun. Correspondingly their luminosities range from 0.1% to about 8% of the solar luminosity. They constitute, at least, 80% of the stellar population in the Galaxy.
Remarkable magnetic activity expressed in extremely strong optical flares was first recorded on UV Cet type stars, while periodic brightness variations were observed in binary systems of red dwarfs as distortions of light curves outside eclipses. Kron (1947, 1952) suggested that they are large spots on the stellar surface that cause these distortions. Subsequent observations by Chugainov (1966, 1971) confirmed this hypothesis. Chugainov also showed that spots are much cooler than the undisturbed photosphere and can cover up to 10% of the stellar surface. A spot model for light curve variations developed by Bopp and Evans (1973) supported the previous findings. This appeared to be extraordinary compared to the Sun. The star with such spottedness, BY Dra, became a prototype of a group of stars exhibiting similar behaviour. Also, this type of variability is often called the BY Dra phenomenon. It is common among binaries with G-K dwarfs as well.
A typical light curve of such a star has a near-sinusoidal shape with an amplitude about 0.1 mag. In addition to the starspot activity, these stars possess powerful chromospheres and coronae, whose activity is exhibited in strong UV, X-ray, and radio emissions and flares.
2.2 Solar-type stars
Stars on the lower main-sequence are known to show chromospheric activity similar to that on the Sun which is detected, e.g., in the Ca ii H & K emission (Wilson, 1978). Shortly after the variability of the Sun in the visual continuum (total irradiance) was established during the Solar Maximum Mission (Willson et al., 1981), evidence for continuum variability among single solar-type stars was also revealed (Radick et al., 1982, 1983a,b). The solar variations, which never exceed a few tenths of a percent, are clearly associated with the disk passage of sunspots and result from a blockage of radiant flux (e.g., Fröhlich, 2002). The amplitude of the stellar variability can be as large as several percent in some cases. It appears to be analogous to the solar phenomenon and is caused by starspots. The survey by Radick et al. revealed that with a precision of about 0.003 mag none of the variable stars had a spectral type earlier than F7 or later than K2, although the list of stars included A0 to K8 candidates. Thus, the starspot phenomenon in solar-type stars peaks seemingly at the effective temperature range from 6400 K to 4900 K.
Evidence linking the photometric variability of solar-type stars to the sunspot phenomenon is provided by the fact that continuum variability seems to occur in anti-phase with variations in Hα and Ca ii H & K emission variations (Dorren and Guinan, 1982). The anticorrelation implies that the surface activity of such stars is confined to localised activity centres that include both emission plages and dark spots, similar to active regions observed on the Sun. Moreover, short-term stellar irradiance variations may be largely explained as rotational modulation by active regions which can persist for several rotation periods (Lockwood et al., 1984).
The onset of solar-type activity at F7 stars with subsurface convection zones was firmly established by the survey of Radick et al., while the reality of the limit at K2 seemed to be less certain. For instance, a higher precision of 0.001 mag achieved aboard the Hubble Space Telescope allowed for the detection of periodic brightness variations of the red dwarf Proxima Cen (V645 Cen, M5Ve) with an amplitude of 0.01 mag and a period of 41.6 d, which were interpreted as rotational modulation of starspots in the stellar photosphere (Benedict et al., 1993).
It was firmly established that magnetic activity in solar-type stars declines with age and that it is closely related to a loss of angular momentum throughout the main-sequence lifetime (Skumanich, 1972; Noyes et al., 1984; Baliunas et al., 1995; Güdel et al., 1997). Thus, young stars exhibit high average levels of activity and rapid rotation, while stars as old as the Sun and older have slower rotation rates and lower activity levels.
2.3 T Tauri stars
T Tau stars were discovered and recognised as a new type of variables by Joy (1945). They are associated with interstellar clouds and distinguished by irregular light variations. Emission lines in their spectra resembling the spectrum of the solar chromosphere are superimposed on photospheric absorption spectra of G-M types of low luminosity. Strongly enhanced lithium absorption in their spectra indicates the young age of these stars. T Tau-type stars are, thus, considered as pre-main-sequence stars of about one solar mass at an age of a few million years, still surrounded by disks of gas and dust remaining from their formation. It was admitted that magnetic fields play an important role in the surface activity of T Tau stars similar to sunspots but strongly enhanced in strength (Petrov and Shcherbakov, 1976; Gershberg, 1982; Appenzeller and Dearborn, 1984), in the flare activity (Guenther and Ball, 1999), as well as in accretion processes and stellar wind phenomena (Hartmann, 1990; Königl, 1991).
A subgroup of T Tau stars with weak emission spectra and little, if any, IR excess radiation, called weak-line T Tau stars, show periodic brightness variations with amplitudes up to 0.5 mag which are caused by very large cool active regions (Bouvier and Bertout, 1989; Petrov et al., 1994; Hatzes, 1995; Grankin et al., 1995). Properties of T Tauri type stars were recently reviewed by Petrov (2003).
2.4 RS CVn stars
RS CVn stars represent a class of close detached binaries with the more massive primary component being a G-K giant or subgiant and the secondary a subgiant or dwarf of spectral classes G to M. They show optical variability (outside eclipses) which is characterised by an amplitude up to 0.6 mag in the V band and interpreted as the rotationally modulated effect of cool spots on their surfaces. Because of low luminosity of the secondary many RS CVn systems appear as singleline binaries which is attractive for spectral analysis. In binaries, where both components can be observed, the primary appears more active than the secondary.
The identification of a new class of variable stars, named after the prototype system RS CVn, was proposed by Hall (1976) who identified the following classification signatures:
-
i.
photometric variability;
-
ii.
Ca ii H & K emission lines;
-
iii.
subgiant component well within its Roche lobe;
-
iv.
fast rotation, i.e. almost synchronised binaries with orbital periods of a few days;
-
v.
orbital period variations.
Since they are tidally locked close binaries, they are also fast rotators. Thus, similar to other cool active stars, RS CVn-type variables are remarkable due to strong chromospheric plages, coronal X-ray, and microwave emissions, as well as strong flares in the optical, UV, radio, and X-ray.
Large amplitude brightness variations of RS CVn stars imply the presence of enormous starspots on their surfaces covering up to 50% of the visible disc (see Section 5). Remarkable activity and high luminosity of these stars make them favourite targets for light curve modelling, Doppler imaging and spectral line analysis. Most of the present knowledge on starspots is based on studies of this type stars.
2.5 FK Com stars
FK Comae stars were first defined as a new group of active stars in the early 1980’s (Bopp and Rucinski, 1981; Bopp, 1981; Bopp and Stencel, 1981). FK Comae stars are late-type giants with spectral types ranging from G to K and rotation periods of only a few days. This indicates very rapid rotation rates. Spectroscopic observations reveal υ sin i values of these stars of ∼ 50–150 km s−1. Still, these stars do not show any significant periodic radial velocity variations and are, therefore, most likely single. Three most active stars of this type are FK Com, V1794 Cyg (HD199178), and YY Men. A few other stars have been suggested as candidates for this group, but they exhibit milder activity and slower rotation.
The magnetic activity of FK Comae stars is revealed by rotationally modulated photometric variations with an amplitude in the V-band of 0.1–0.3 mag caused by cool asymmetrically distributed spots on the stellar surface. Other characteristics of these stars include a very strong and variable chromospheric emission in the Ca ii H & K lines and in the Balmer lines. The photometric and spectroscopic characteristics of FK Comae stars are very similar to those of the very active RS CVn stars (see Section 2.4), with the exception that RS CVn stars are close binary systems in which the tidal effects produce synchronous rotation and, therefore, also rapid rotation.
The origin of FK Comae stars is still debated. A few evolutionary scenarios have been proposed for explaining the odd rapid rotation of the late-type single giants. The first idea on the origin of FK Comae stars was that the stars may represent the further evolution of W UMa contact binaries (see Section 2.6) into a coalesced single star (Bopp and Rucinski, 1981; Bopp, 1981; Bopp and Stencel, 1981). Such a scenario was first considered by Webbink (1976) who calculated the evolution of a contact binary and showed that the mass ratio (secondary/primary) can decrease on an evolutionary time scale until the secondary is completely dissipated, during the primary’s initial ascent of the giant branch. The kinematics and age of FK Com support this hypothesis (Guinan and Robinson, 1986). However, as argued by Fekel and Balachandran (1993), the detection of lithium in these active giants is evidence against binary coalescence. They considered a scenario in which the surface convection zone reaches the rapidly rotating core just as a star begins its first ascent of the giant branch, and dredges both high angular momentum material and freshly synthesised Li to the surface. Still, the puzzle is not solved and requires further investigation of these objects.
2.6 W UMa stars
W UMa stars are eclipsing binaries with periods between about 5 and 20 h showing continuous light variations (Selam, 2004). They consist of two solar-type components surrounded by a common envelope. A large-scale energy transfer from the larger, more massive component to the smaller, less massive one results in almost equalising surface temperatures over the entire system. The components of such a contact binary rotate very rapidly in spite of their old ages (v sin i ∼ 100–200 km s−1) as a result of spin-orbit synchronisation due to strong tidal interactions between the stars. W UMa stars are very common, comprising some 95% of eclipsing binary variables in the solar neighbourhood, or one star in every 1000–2000 in the same spectral range (Eggen, 1967).
Observations reveal that there are two subclasses of W UMa stars: A-type and W-type systems. The former have longer periods, are hotter, have larger total mass, and a smaller mass-ratio and are in better contact. The effective temperatures of the primary and secondary stars in W Uma-type variables are not exactly the same. In W-type the temperature difference is larger and the secondary appears hotter, while in A-type the primary is hotter or almost the same temperature as the secondary. Mullan (1975) suggested that the primary stars in W-type systems appear cooler relative to the secondary due to cool magnetic starspots on their surfaces. Following this idea, photometric peculiarities of such systems have been often interpreted with the help of either cool or hot spots on the binary components. A study of the contact binaries with Doppler imaging technique (see Section 4.2) reveals that both components can be covered by cool starspots, with a tendency for the primary to be more active than the secondary (Maceroni et al., 1994; Hendry and Mochnacki, 2000; Barnes et al., 2004).
2.7 Algols
Algols are eclipsing binaries consisting of a hot, main-sequence primary star of spectral class B to F and a cool, evolved, less massive secondary. Cool stars in Algols are usually G or K subgiants with outer convection envelopes which are in contact with their Roche lobes. Tidal interactions force most of these stars to rotate synchronously with their orbital motions, producing typical rotational velocities between about 30 and 100 km s−1. The rapid rotation combined with deep convection envelopes produces a variety of magnetic activity phenomena including starspots in these stars, similar to RS CVn (see Section 2.4), BY Dra (see Section 2.1), and W UMa binaries (see Section 2.6). Hall (1989) summarised observations indicating magnetic activity in Algols. In addition to strong Ca ii H & K emission, X-ray, and radio emission was detected from a number of Algol binaries which indicated the presence of hot coronae associated with the cool stars (White and Marshall, 1983; Stewart et al., 1989; Umana et al., 1989).
Brightness variations due to starspots can be observed in Algols only during primary total eclipses, when the luminous hot components are hidden. Therefore, because of synchronised rotation, only one hemisphere of the cool Algol stars can be observed and the photometric data collected are less detailed than for other spotted binaries. Photospheric continuum variations were nevertheless detected in cool components and attributed to the effect of cool starspots (Richards, 1990; Olson and Etzel, 1993; Varricatt, 2000).
2.8 Degenerate stars
If the magnetic flux is conserved during stellar evolution, white dwarfs should be expected to have magnetic fields of 107–108 G. Yet, isolated magnetic white dwarfs are quite rare, comprising about 5% of all white dwarfs (Wickramasinghe and Ferrario, 2000). Observed spectral variations of magnetic white dwarfs on a timescale of hours or days suggest a complex magnetic field distribution on their surfaces. In some cases, spot-like magnetic field enhancements superimposed on a weaker dipole magnetic field can be identified (Landi Degl’Innocenti, 1976; Maxted et al., 2000). Similar structures are most probably present on the surfaces of neutron stars as well. There is a growing evidence, based on X-ray and radio observations, that besides the large-scale dipolar magnetic field, isolated neutron stars possess small-scale magnetic field enhancements (Geppert et al., 2003). Current theory predicts that such structures can be generated from strong subsurface toroidal fields on both white dwarfs and neutron stars.
3 Observational Tools for Studying Starspots
3.1 Photometry
Since the discovery of the first indications of starspots, photometry remains the most common technique for studying stellar activity. Thanks to efforts of individual observers, more or less regular observations of spotted stars began in 1970’s. They are currently supported by a great number of Automatic Photometric Telescopes (APTs) which provide every-night routine measurements for a big sample of stars. At present, more than a dozen APTs with apertures of 20 cm to 1.2 m operate around the world (see Table 1). The accuracy of ground-based APTs is about 2–5 mmag.
A vast amount of photometric data have been also obtained by the ESA mission HIPPARCOS with the accuracy down to 1 mmag (van Leeuwen et al., 1997). Future space missions aiming at studying stellar oscillations and detection of earth-size exoplanets will also provide immense high-precision photometry of nearby stars which can be used for studying starspots:
-
COROT http://sci.esa.int/science-e/www/area/index.cfm?fareaid=39
-
Gaia http://sci.esa.int/science-e/www/area/index.cfm?fareaid=26
-
MOST http://www.utias-sfl.net/microsatellites/MOST/MOSTIndex.html
3.2 Spectroscopy
Spectroscopy is one of the main tools of modern astrophysics. Almost all we know about the physical properties of astrophysical objects comes from the analysis of their spectra. Studying starspots requires high-resolution spectrographs (Δλ/λ ≥ 50 000) with high-sensitivity detectors which have become available for the past two decades at mid and large aperture telescopes. Among 8–10 m telescopes it is worth tomention UVES at VLT, HIRES at KECK, HRS at the Hobby-Eberly Telescope (HET), and HDS at Subaru. In addition, there are about 10 high-resolution spectrographs on 4 m class telescopes and even more on 2 m class telescopes. Most of them are echelle cross-dispersed spectrographs allowing for a wide wavelength range in the optics. A recent overview of the currently available high-resolution spectrographs and future projects was given by Pallavicini (2002).
A study of starspots involves routine monitoring and data collection for a relatively large sample of stars. A great help comes from using robotic telescopes. The first dedicated robotic telescope T-13 was developed at the Tennessee State University and has started its operation in 2003 at the Fairborn observatory, Arizona (http://schwab.tsuniv.edu/t13/description.html). It is a 2 m telescope with a spectrograph working at two resolutions, 34 000 and 90 000, and full wavelength coverage in the optical. The second spectroscopic robotic telescope STELLA I of 1.2 m is being built by AIP and IAC. It is expected to start operation in 2006 on Tenerife and will be equipped with echelle spectrograph of maximum 50 000 resolution (http://www.aip.de/stella/). The two telescopes are planned to be complementary in studying starspots, as they are separated by about 95° in longitude and, thus, will allow prolonging an observing night by 6 h.
3.3 Polarimetry
The most direct way to detect and study stellar magnetic fields is to use polarimetric techniques. Polarimetry of stars other than the Sun is, however, a rather challenging task and represents a relatively small field of stellar astrophysics. This, on one hand, is due to limited instrumental capabilities and, on the other hand, due to disk-integrated observations of the Stokes parameters. The latter results in significant cancellation of the signal from regions of mixed polarity fields and, thus, only large-scale magnetic fields can be detected from disk-integrated polarimetric measurements, which still requires the accuracy of the order 10−3–10−4. Such low polarimetric signals from starspots require large collecting areas of telescopes. An overview of the existing instruments and future projects was made by Semel and López Ariste (2001). A list of the available instruments is given in Table 2.
The new generation large telescopes are not yet equipped with high-resolution spectropolarimetric capabilities. The only existing project is PEPSI at the double 8 m LBT (Strassmeier et al., 2004). Low-resolution spectropolarimetry is possible with FORS1 at VLT (Appenzeller et al., 1998). A promising approach to high-precision polarimetry is provided by a ZIMPOL-type spectropolarimeter, which is a transportable system being combined with a spectrograph (Stenflo, 2001).
Magnetic fields in G, K, and M main-sequence stars have been deduced from the broadening of line profiles (e.g., Valenti et al., 1995) or even Zeeman-split spectral lines in M-type dwarf flare stars (Johns-Krull and Valenti, 1996). Using SEMPOL at AAT, Donati et al. (1997) reported detection of Zeeman polarisation in several kinds of active stars, including RS CVn systems, a dwarf flare star of BY Dra type, a FK Com star, and a T Tau star. Several new detections have been made with MuSiCoS (Wade, 2003).
3.4 Interferometry
Optical interferometry can be a powerful technique to image inhomogeneities on stellar surfaces. Direct observations of starspots will be the key constraints for models of stellar activity.
A stellar long-baseline interferometer consists of an array of several separate telescopes, which redirect starlight to a central location where interference fringes are formed. The angular resolution that the interferometer can achieve depends on the baseline (the telescope separation), while for a single telescope the resolution is defined by its aperture diameter. The angular resolution is proportional to the ratio of the wavelength to the baseline of the interferometer or the diameter of the telescope. The largest existing telescope is 10 m in diameter, whereas the largest interferometer has a baseline of 600 m, giving the latter a factor of 60 increased resolving power.
If the interferometer is coupled with a spectrograph, fringes can be analysed along spectral domains. Such a spectro-interferometer allows for eliminating disturbances by the Earth atmosphere and measure differential phases between two wavelengths, i.e., carry out colour differential interferometry (Petrov, 1988). For magnetically active stars such observations can provide orientation of the stellar rotation axis with respect to the line of sight (Lagarde et al., 1995), which is important for interpretation of spectroscopic and photometric observations of spotted stars. Also, differential fringe phases can be used to locate spots on the stellar surface (Wittkowski et al., 2002; Jankov et al., 2003; Rousselet-Perraut et al., 2004), even in such difficult cases as pole-on and equator-on orientations of the star which cannot be resolved by traditional Doppler spectroscopy. In addition, the stellar differential rotation rate and the inclination angle can be disentangled (de Souza et al., 2004).
A spectro-interferometer equipped with a polarimeter allows for recording the visibility function and fringe phase for different polarisation states and, thus, can provide measurements of local magnetic fields on the stellar surfaces (Rousselet-Perraut et al., 2004), which is the key information for studying stellar magnetic activity.
A list of the available and planned for the near future instruments is given in Table 3.
3.5 Microlensing
Gravitational imaging of stellar photospheres is a potentially useful tool for stellar astrophysics. Detecting spots in ways different from, e.g., rotationally induced modulations of the stellar brightness or spectral line profiles could bring considerable insight into their properties. For instance, microlensing can help to disentangle the temperature and spot area. Moreover, it provides an opportunity for probing starspots on the surfaces of slow rotating stars, which are unsuitable candidates for the Doppler imaging technique.
A microlensing event has been recently used for high-precision, multicolour measuring a limb darkening profile on the surface of a K3 giant and revealed a significant disagreement between the observed and predicted from atmospheric models disk brightness distribution (Fields et al., 2003). The Optical Gravitational Lensing Experiment (OGLE) survey of bulge giants provided photometric evidence for stellar spots via microlensing events (Udalski et al., 1995). Modelling of the spots on the stars selected from the OGLE database was undertaken by Guinan et al. (1997). Further theoretical investigation of possible detections of stellar spots by gravitational microlensing was carried out by Heyrovský and Sasselov (2000) and Hendry et al. (2002). They concluded that starspots generally produce a clear signature only for transit events. Moreover, this signature is strongly suppressed by limb darkening for spots close to the limb, although spots may still be clearly detected for favourable lens trajectories. It was found also that in order for microlensing events to be an effective starspot imaging tool, intensive temporal sampling throughout the transit is needed.
4 Diagnostic Techniques for Studying Starspots
4.1 Light-curve modelling
Since the discovery of stellar photometric variations due to cool spots, generally two approaches are used to model such variations and to deduce starspot properties. One is based on a trial-and-error direct light-curves modelling (LCM) when assuming a number of circular (or of other pre-defined shape) spots causing the variations. Numerical techniques employing this approach have been developed by Budding (1977), Vogt (1981), Rodonò et al. (1986), Dorren (1987), Strassmeier (1988) and Kiurkchieva (1990). A technique taking into account time evolution of starspots has been proposed by Strassmeier and Bopp (1992). It allowed for detecting spot appearance and disappearance on time scales from a few to a hundred days. A zonal model with (near-)equatorial inhomogeneous bands of spots was considered by Eaton and Hall (1979) and Alekseev and Gershberg (1996).
A disadvantage of the above mentioned models is that they have many free parameters and the shape of spots or of spot distribution has to be assumed. Moreover, the solution is not unique. To avoid many assumptions, an alternative approach performing light-curve inversion (LCI) into an image of the stellar surface has been developed. An inversion technique is usually applied to the photometric light curves in the two temperature approximation. The model assumes that, because of low spatial resolution, the intensity of each pixel on the surface Ii contains contributions from both temperature components, the hot photosphere Ip, and cool spots Is weighted by the fraction of the surface covered with spots fi (spot filling factor):
with 0 ≤ fi ≤ 1. The instantly observed stellar flux is the integral of the intensity contributions from the surface elements seen at a given rotational phase. The inversion of the light curve results in a distribution of the spot filling factor over the stellar surface, i.e., stellar image. Figure 1 shows examples of light curves and maps of the spot filling factor obtained from them for the RS CVn type star σ Gem. Since a light curve represents a one-dimensional time series, the resulting stellar image contains information on the spot distribution only in one direction, in longitudes, while spot extents and locations in latitudes remain uncertain. As a result, maximum spot concentration always appears at the central latitude of the stellar disk whose value depends on the assumed inclination of the rotational axis. Because of the projection effect and limb darkening, images show more well defined structures than the light curves and, therefore, are very useful for determining longitudes of spot concentrations. Numerical techniques based on such an approach have been elaborated by Messina et al. (1999) and Berdyugina et al. (2002).
Light curve inversion results for the RS CVn star σ Gem (Berdyugina & Henry, in preparation). The first and third columns are maps of the spot filling factor. Darker regions indicate larger values. Observed and calculated V-band light curves are shown in the second and fourth columns by crosses and lines, respectively. The images also illustrate a flip-flop event that occurred in 1988: the active region near the phase 0.5 has diminished for about one year, while the region near the phase 0.0 has increased in size (see discussion of the flip-flop phenomenon in Section 6.2).
More detailed information on the spot pattern from light curves can be obtained in the case of eclipsing binaries by the eclipse mapping technique. This method employs the opportunity to scan the stellar disk in finer detail by the eclipsing companion. The inversion techniques based on the Maximum Entropy and Tikhonov regularisation methods (see Section 4.2) were developed by Rodonò et al. (1995), Collier Cameron (1997), and Lanza et al. (1998a).
Inversion or modelling of light-curves is clearly less informative than techniques which are based on spectroscopic observations. Continuous and frequent photometric data allow though for conclusions on longitudinal spot patterns and their long-term evolution (Section 6).
4.2 Doppler Imaging
During the last two decades the Doppler imaging technique has been extensively employed for studying starspots on active stars. The main idea of the technique is to use high-resolution spectral line profiles of rapidly rotating stars for mapping the stellar surface. This idea was first formulated by Deutsch (1958), while the first inversion technique with minimisation was developed by Goncharskii et al. (1977). It was first used for mapping chemical peculiarities on the surface of Ap stars. Modelling of photometric variations of late-type active stars has revealed that cool starspots are often quite large, covering up to 20% of the stellar surface. Such starspots should have resulted in noticeable line profile variations which were first observed in spectra of the RS CVn-type star HR 1099, and from which the first Doppler image of a spotted star was obtained by Vogt and Penrod (1983).
The Doppler imaging technique aims to restore starspot distribution information which is contained in time varying line profiles of rotating stars. If the star rotates rapidly enough, so that the rotation broadening of a line profile is significantly larger than the local line profile at a single point on the stellar surface, then a cool spot on the stellar surface will result in a “bump” in the profile (Figure 2). This “bump” moves across the profile, as the star rotates, with the velocity amplitude depending on the spot latitude. Inversion of a time series of the stellar line profiles results in a map, or image, of the stellar surface.
Spectral line profiles for a model fast rotating star with no spots (dashed line) and with a spot moving across the disk as the star rotates (solid line). See also animation at http://www.astro.phys.ethz.ch/staff/berdyugina/private/StellarActivity/StellarAct.html
An assumption on the nature of starspots is the main part of the model calculations. Cool spots will modify the flux integrated over stellar disk. Therefore, the intensity of radiation I(T(s), λ, μ) emitted by the stellar surface from the point s in the direction μ at the wavelength λ is defined by the local temperature T(s), which is assumed to be the effective temperature of the model atmosphere used for the calculation of the local line profile at the point s. Integration over the stellar disk, given rotational phase ϕ and set of wavelengths, results in the residual flux rλ(ϕ) which contains information on the temperature distribution on the stellar surface T(s) and, therefore, is to be compared with the observed residual flux \(r_{\lambda}^{\rm obs}(\phi)\). Thus, the integration determines the direct transformation for a subsequent inversion. A comparison of the residual fluxes determines the discrepancy function D(T). By minimising D(T), one can obtain a unique solution with minimum variance. Such a solution is not however feasible due to noise in data. Smoothing the noise results in a multitude of different stable solutions. Searching for the unique and stable solution is a so-called ill-posed inverse problem, and there are different approaches and methods developed for solving it.
A common way of choosing the unique solution with a given level of goodness of the fit is to invoke some additional constraints R(T), which usually determine special properties of the solution. Therefore, the original ill-posed minimisation problem is replaced by another, which has a unique solution:
where A is a Lagrange multiplier and R(T) is a regularisation functional, which makes the solution unique. The value of Λ should be selected so that if T(s) minimises Φ(T), then the rms deviation of the fit of the profiles is of the order of the noise in the observations.
Methods developed with such assumptions differ by the definition of R(T). The Tikhonov regularisation method (TRM), applied by Goncharskii et al. (1977) and Piskunov et al. (1990), claims the solution to be with the least gradient of the parameters, and R(T) = grad T. The Maximum Entropy method (MEM) first applied by Vogt et al. (1987) searches for the solution with the largest entropy, and R(T) = T log T. Generally, the two methods assume that the observed phenomena possess properties R(T), which cannot be known a priori. For instance, in case of surface imaging both above assumptions cannot be proved by the observations. In fact, for choosing a unique solution, one indeed needs some additional information, and, if it is not available, it is substituted by some plausible assumptions, which lead to an apparently acceptable solution but with an unknown bias. One should note, however, that in case of data of high quality and quantity the role of the regularisation is reduced, and the solution is approaching to the maximum likelihood solution, which in this case could be also considered as an acceptable result.
An alternative Occamian approach (OA) to inverse problems was developed by Terebizh (1995) and applied to the Doppler imaging problem by Berdyugina (1998). In the Occamian approach the choice of a solution is based on the analysis of information contained in observations and the transformation model. Building the Fisher information matrix F with eigenvectors V one defines a new reference frame with coordinates Y, which are linear combinations of the unknown parameters T:
The new coordinates Y comprise principal components of the solution. Small eigenvalues of F indicate principal components with relatively large errors of the solution, so that the error ellipsoid is extremely elongated in these directions. Moreover, in case of a lack of data some of the eigenvalues become zero, and the corresponding parameters are linearly dependent. Therefore, only a part of the principal components Y(p) completely exhausts the available information on T. In such a case, the Y(p) are estimated instead of T, while other principal components with not enough information are assumed to be zero. Then, the transformation
leads to the desired unique and stable solution \({\tilde T}\). Thus, the solution in the Occamian approach is the one which statistically satisfactorily fits the observed data with a minimum set of \({\tilde Y}^{(p)}\). Such a solution is unique because of the choice of p and stable because of removing those principal components which contain no significant information but noise. It is not constrained with any artificial assumptions. Another advantage of the Occamian approach is that the inverse Fisher information matrix gives estimates of the variances of the solution.
A number of numerical codes for Doppler imaging of cool stars based on the Maximum Entropy method have been developed by Vogt et al. (1987), Rice et al. (1989), Brown et al. (1991), Collier Cameron (1992, 1995), Jankov and Foing (1992), and Rice and Strassmeier (2000). Piskunov et al. (1990) used the Tikhonov regularisation method and Berdyugina (1998) the Occamian approach. A technique based on the CLEAN-like approach was suggested by Kürster (1993) and one based on the interferometry by Jankov et al. (2001). Effects of different numerical methods was investigated by Piskunov et al. (1990) (MEM and TR), Strassmeier et al. (1991) (MEM, TR, trial-and-error), Kürster (1993) (CLEAN and MEM), and Korhonen et al. (1999) (TR and OA). As mentioned above, the difference is diminished when the data used are of high quality.
Important inputs for Doppler imaging which affect significantly the result are stellar atmosphere models, atomic and molecular line lists and stellar parameters. Errors in calculations of local line profiles have a strong effect on the inversion for moderate rotators. They easily cause artificial features in maps, like polar caps and belts of cool and hot spots (Unruh and Collier Cameron, 1995). The same features are obtained in case of a wrong value of the stellar rotational velocity and a wrong estimate of the effective temperature of the star (Berdyugina, 1998). Spot latitudes strongly depend on the inclination angle of the rotational axis to the line of sight. Various tests showed that capabilities of the technique are limited in the equatorial region where spots are recovered with reduced area and contrast. Sub-equatorial spots cannot be restored, especially at lower inclinations. A recent overview of the strengths and weaknesses of the Doppler imaging technique was given by Rice (2002).
Doppler imaging of a single star with the inclination angle of the rotational axis to the line of sight close to 90° (equator-on) experiences difficulties in recovering spots on either side of the stellar equator because of the symmetry of Doppler shifts in line profiles with respect to the equator. In a binary system such an inclination angle of the binary orbit would lead to eclipses of the components. For an eclipsing binary, the equatorial symmetry problem is reduced, and the quality of the mapping can be improved (Vincent et al., 1993).
For the last two decades more than 60 cool stars have been studied with the surface imaging technique (see, for an overview, Strassmeier, 2002). Out of them 29 are single stars and 36 are components in close binaries. A dozen of stars have been monitored for several years. The total number of Doppler images is 245 as of June 2002 (http://www.aip.de/groups/activity/DI/summary/). The results obtained with the Doppler imaging techniques are discussed in Section 5. Examples of stellar Doppler images are shown in Figures 6 and 15.
4.3 Zeeman-Doppler Imaging
As an extension of the temperature and abundance mapping of the stellar surface, a magnetic Zeeman-Doppler imaging (ZDI) method was introduced by Semel (1989) and further developed by Donati et al. (1989), Semel et al. (1993), Brown et al. (1991), and Donati and Brown (1997). The technique is based on the analysis of high-resolution spectropolarimetric data and allows for disentangling magnetic field distribution on the stellar surface due to different Doppler shifts of Zeeman-split local line profiles in the spectrum of a rotating star (Figure 3). In the absence of rotation, the net circular polarisation signal in spectral lines would be zero due to mutual cancellations of contributions of regions of opposite field polarity.
Observed circular polarisation in the spectrum (panel b) is a sum of opposite polarity Stokes V profiles due to spots located at different Doppler shifts (panel a). From Semel (1989). See also explanatory animations by P. Petit at http://webast.ast.obs-mip.fr/people/petit/zdi.html
Zeeman signatures in atomic lines due to starspots are expected to be extremely small, with typical relative amplitudes of 0.1%. Detecting them requires measurements of polarisation with noise level in Stokes V as low as 10−4, while the current instrumentation allows for the best relative noise level of 10−3. Semel (1989) and Semel and Li (1996) proposed a multi-line approach for increasing the signal-to-noise (S/N) ratio of the measured polarisation, which has resulted in first detection of the circular polarisation signal in a cool star (Donati et al., 1997). A combination of Stokes V profiles using a multi-line technique called Least Squares Deconvolution (LSD) is based on the weak field approximation, i.e., one assumes that the magnetic splitting of spectral lines is smaller than their local Doppler broadening. In this case the Stokes V signal is proportional to the derivative of the intensity profile I(υ), i.e.,
where gi is the effective Lande factor and λi is the wavelength of the i-th spectral line. It is assumed further that the local line profiles are self-similar and scale in depth and width with the central depth di and wavelength, i.e.,
where Z(υ) is a so-called mean Zeeman signature, which is constant for all lines. The LSD Stokes V profile can be obtained as a sum over many individual lines:
Blends and splitting patterns should be treated explicitly for each line. The gain factor in the S/N ratio can be as large as 30 when using more than 2000 line profiles. The LSD technique allowed for detection of magnetic fields on various types of cool stars, from pre-main-sequence stars to evolved giants (Donati et al., 1997). It was also used for temperature mapping using Stokes I observations of faint stars with short rotational periods for which high signal-to-noise spectra cannot be obtained through longer exposure times.
Applying an inversion technique, similar to those used for Doppler imaging (see Section 4.2), to all four Stokes parameters, one can recover the distribution of the temperature and magnetic field vector over the stellar surface. Three numerical codes based on the Maximum Entropy method (Brown et al., 1991; Hussain et al., 2000) and the Tikhonov regularisation (Piskunov and Kochukhov, 2002) have presently been developed. In practice, however, measuring the full Stokes vector for cool stars is difficult, because magnetic signatures in Stokes Q and U are considerably smaller than in Stokes V. Obtained Zeeman-Doppler images of cool stars are based on measurements of only Stokes I and V are certainly not unique and provide limited information for the interpretation. A lack of information on different components of the magnetic vector can be overcome by assuming a certain relation between the components. For instance, Hussain et al. (2001) prescribed the field to be potential and reconstruct its distribution from circularly polarized line profiles. Piskunov and Kochukhov (2002) suggested a special type of regularisation based on spherical harmonic expansion. In this case the field distribution is forced to take the form of such an expansion which is acceptable only for stars with clearly dominating multipole structures like, e.g., Ap stars.
In the inversion procedure three components of the magnetic field vector are generally represented by radial, azimuthal, and meridional fields. To some extent they contribute to the line of sight component observed in Stokes V at different rotational phases and different Doppler shifts. For instance, the radial field will dominate the Stokes V near the centre of the stellar disk, while the azimuthal field will be most noticeable in the circular polarisation near the stellar limb. This allows to recover some parts of the magnetic field components from Stokes V observations. An example of such restoration is shown in Figure 4. When interpreting the results of Zeeman-Doppler images obtained only from Stokes I and V, one has to take into account that the magnetic field distribution is underdetermined for each component and that there might be a cross-talk between different components (Donati and Brown, 1997).
Zeeman-Doppler images of the young active K0 dwarf AB Dor. From Donati and Collier Cameron (1997).
4.4 Molecular bands modelling
Molecular lines provide evidence of cool spots on the surfaces of active stars. If the effective temperature of the stellar photosphere is high enough, molecular lines can only be formed in cool starspots. The first detection of molecular bands from starspots was reported by Vogt (1979) for a star whose spectral type K2 was not compatible with the presence of TiO and VO bands. From the relative strengths and overall appearance of the molecular features, an equivalent spectral type of the spot spectrum was estimated as late as M6. A phase-dependent variation in the strength of the TiO band was detected by Huenemoerder et al. (1989), with TiO being strongest at the photometric minimum. This confirmed that the photometric modulation is indeed caused by cool spots. Moreover, a comparison of photometric variations with TiO band strengths provided reliable estimates of unspotted stellar magnitudes (Berdyugina et al., 1998b, 1999b).
A technique for determining spot filling factors and temperatures from molecular band modelling (MBM) was suggested by Huenemoerder and Ramsey (1987) and further developed by Neff et al. (1995) and O’Neal et al. (1996). They modelled the observed spectrum by combining spectra of suitable standard stars of different effective temperatures weighted by spot filling factor and continuum surface flux ratio. For instance, observations in two TiO bands of different temperature sensitivity, at 7055 Å and 8860 Å, were combined to estimate the area and the temperature of spots.
Since TiO lines are only formed in starspots on the surfaces of G-K giants and subgiants, polarisation observations in these lines can provide measurements of magnetic fields directly in spatially unresolved spots. As shown in Figure 5, the TiO lines at 7055 Å are rather strongly magnetically sensitive, having effective Lande factors up to 1 (Berdyugina and Solanki, 2002; Berdyugina et al., 2003). The wavelength separation between rotational lines in the band is small and lines of low rotational numbers (larger splitting) almost coincide with those of high numbers (smaller splitting) in the band head. Nonetheless, a clear Stokes V signal should be measured from starspots Berdyugina (2002).
Calculated (solid line) and observed (dashed line) Stokes V profile for the TiO γ(0,0)R3 band head in a sunspot. The field strength is 3 kG and the filling factor is 0.75 for an angle between the magnetic vector and the line of sight of 0°. Vertical dashes indicate positions of lines included in the spectral synthesis. From Berdyugina (2002).
An excess of the absorption in the infrared OH lines at 1.5 µm due to starspots has been detected by O’Neal and Neff (1997) and O’Neal et al. (2001). Since OH lines can be observed at higher temperature than TiO, starting from 5000 K and below, they can be used for studying starspots on hotter stars. Otherwise, they are contaminated by the photospheric contribution, which should be carefully taken into account. On the other hand, OH lines provide a greater temperature range over which starspots can be detected through molecular absorption features.
4.5 Line depth ratios
Spots on slowly rotating stars can be studied by photometric and spectroscopic molecular line techniques. To discriminate between spot temperature and spot area, these techniques use at least two independent measurements, brightness and colour in photometry and different molecular bands in spectroscopy. The Line Depth Ratio (LDR) technique offers an opportunity to resolve temperature variations with unprecedented accuracy of less than 10 K (Gray, 1996). A technique for studying starspots with LDR was developed by Catalano et al. (2002). It is based on the analysis of depth ratios of a pair of lines, one insensitive and one very sensitive to temperature. Due to presence of a dark spot that produces a decrease of say 10% in the continuum, the depth of both lines would be equally affected and reduced by 10%, while their depth ratio would remain unchanged. Due to the lower temperature of the spot, however, the temperature sensitive line will change its intrinsic depth and, thus, the depth ratio of the two lines will change as well. The amount of depth ratio variation depends on the temperature variation and the fraction of surface covered by spots. Catalano et al. (2002) proposed 10 pairs of lines in the 6100–6200 A wavelength range and calibrated them against effective temperatures of main-sequence stars and giants. Their results for active stars are discussed in Section 5.1. Frasca et al. (2005) combined the LDR technique with the analysis of simultaneous light curves. This technique enables disentangling the spot temperature and area.
4.6 Asteroseismology
Magnetic activity influences the internal stellar structure. In the case of the Sun, this is observed as shifts of eigenfrequencies of global modes of solar oscillations (Woodard and Noyes, 1985). Mode frequencies increase with magnetic activity: for the 11-yr cycle, low-degree mode frequencies are shifted by the order of 10−4. The study of high-degree modes has revealed that frequency shifts are caused by structural perturbations near the solar surface which are localised in latitude (Libbrecht and Woodard, 1990). Thus, measurements of frequency shifts on solar-type stars is a potential tool for studying starspot latitudes. Lanza and Rodonò (2002) studied the possibility for asteroseismic tests of the internal structure of magnetically active close binaries. Gizon (2002) investigated prospects for detecting stellar activity through asteroseismology. He concluded that observations of solar-like oscillations contain measurable information about the latitudinal distribution of stellar activity under the following conditions: The stellar rotation is high enough to resolve frequencies of different azimuthal numbers; stellar activity is strong enough to produce significant spotted area, and the inclination angle of the stellar rotation axis is larger than 40°. Still, observations should be long and continuous, which can be provided by the future space missions COROT (http://iaa13u.iaa.csic.es/~corot/mainE.html) and Kepler (http://www.kepler.arc.nasa.gov/).
Stellar differential rotation for solar-type stars can be measured through asteroseismology as well (Gizon and Solanki, 2004). Rotationally split frequencies of global oscillation provide information about rotation at different latitudes depending on the azimuthal order m of the mode of pulsation. Since the m = ±1 and m = ±2 components of quadrupole oscillations can be observed simultaneously in asteroseismology, rotational frequency splittings can be inverted to provide an estimate of the difference in stellar angular velocity between the equator and 45° latitude. The precision of the method depends on the value of the mean rotation and on the inclination angle between the rotation axis and the line of sight.
5 Starspot Properties
5.1 Temperature and filling factor
Observed amplitudes of the optical brightness modulation imply that a large fraction of the stellar photosphere is covered by cool starspots. The largest ever observed light-curve amplitude ΔV = 0.65 mag of a spotted star was reported for the weak-line T Tauri type star V410 Tau (Strassmeier et al., 1997). Two RS CVn-type stars HD 12545 and II Peg have been observed at the largest ΔV = 0.63 mag by Strassmeier (1999) and Tas and Evren (2000), respectively. Such big amplitudes in brightness variations are accompanied by large in-phase variations of a colour, suggesting the presence of cool spotted areas covering up to 20% of the entire stellar surface or about 40% of the stellar disk (Figure 6).
Doppler image of the RS CVn type star HD 12545 at the time of its largest amplitude of brightness variations. From Strassmeier (1999).
Our current knowledge on starspot temperatures is based on measurements obtained from simultaneous modelling of brightness and colour variations, Doppler imaging results, modelling of molecular bands and atomic line-depth ratios, the latter being the most accurate method. A representative sample of starspot temperatures for active dwarfs, giants and subgiants is collected in Table 5 and plotted in Figure 7. As seen from the plot, there is a clear tendency for spots to be more contrasting with respect to the photosphere in hotter stars: the temperature difference between spots and the photosphere decreases from about 2000 K in G0 stars to 200 K in M4 stars. There seems to be no difference in this property between active dwarfs and giants, at least for G-K stars, that implies the nature of starspots to be the same in all active stars. Also a weak-line T Tauri star V410 Tau seems to follow the relation. The only exception found is a young solar analogue EK Dra whose starspot temperature, estimated from light-curve modelling and Doppler imaging, significantly deviates from the relation. However, the value obtained from molecular band modelling fits the sequence quite well (O’Neal et al., 2004).
Spot temperature contrast with respect to the photospheric temperature in active giants (squares) and dwarfs (circles). Thin lines connect symbols referring to the same star. The thick solid line is a second order polynomial fit to the data excluding EK Dra. Dots in circles indicate solar umbra (ΔT = 1700 K) and penumbra (ΔT = 750 K) (based on data in Table 5).
High filling factors, up to 50% of the stellar disk, have been determined by O’Neal et al. (1996, 1998) from modelling molecular bands observed in the spectra of spotted stars (see Section 4.4). For instance, for the very active RS CVn-type star II Peg they derived a spot temperature of about 3500 K and a filling factor varying between 43% and 55%. Such large spot filling factors were found also for other active stars (O’Neal et al., 1996, 2004). They apparently contradict to Doppler imaging results. This suggests that Doppler images may not easily reveal the absolute spot coverage and, perhaps, leave unnoticed non-modulating and unresolved spots. An excess of the absorption in molecular bands implies that even at the maximum brightness stellar photospheres have a substantial spot occupancy. Note, however, that molecular band modelling is rather sensitive to the assumed photosphere temperature and chemical composition as well as to Doppler shifts accross the spots which may affect the spot filling factor (Berdyugina, 2002; O’Neal et al., 2004).
Large spot areas and spot temperature contrasts recovered on active stars suggest that photometric and spectroscopic variability of these stars is dominated by the starspot umbra. Low temperature contrast of spots and small spot filling factors in M dwarfs, as well as contradictory results for EK Dra obtained by different methods, can be due to a decreasing of individual spot sizes and, thus, increasing relative contribution from the spot penumbra. For instance, the spot contrast obtained from Doppler imaging and light-curve modelling for EK Dra corresponds to the temperature contrast of the sunspot penumbra. Accordingly, we should expect that active late F-type stars possess spots with dominating penumbra and, thus, show lower contrast spots. As in the case of EK Dra, observations in molecular bands are more reliable for detection of starspot umbra.
5.2 Magnetic field
Direct measurements of magnetic fields on the surfaces of cool stars are very difficult. The net circular polarisation of the Sun as a star would be hardly observable with the present observational tools, as the mean magnetic field of the Sun peaks at maximum 8 G.
The ZDI technique (Section 4.3) is an excellent tool for detecting surface magnetic fields. Donati et al. (1999) combined Stokes V of more than thousand lines and obtained a time sequence of mean V profiles which shows clear rotational modulation, as magnetic structures are carried across the visible hemisphere of the star. This technique is useful for rapidly rotating stars as the rotation disentangles surface magnetic structures with opposite polarities, reducing polarisation cancellation (see Figure 3). On slower rotators the ZDI technique can only reveal large-scale unipolar magnetic fields. It has been intensively used for studying three stars: young dwarfs AB Dor and LQ Hya and RS CVn star HR1099 (Donati et al., 2003b, and references therein). An example of the spot and magnetic field distribution obtained with the ZDI technique is shown in Figure 4. The common feature of reconstructions for the three stars is that the magnetic field distribution does not coincide with the darkest spots in the temperature images. The radial field component reveals large mid-latitude regions of mixed polarity, while the azimuthal component appears as almost axisymmetric rings of opposite polarities at higher and lower latitudes. Donati et al. (2003b) interpreted such a field distribution as an indication of large-scale poloidal and toroidal field components on the stellar surface and the underlying dynamo processes distributed throughout the entire convection zone. It was, however, argued by Solanki (2002) that the rings of the azimuthal field may represent large penumbral regions with a predominantly horizontal magnetic field.
Most of our current knowledge about magnetic fields on cool stars and in starspots is, however, based on Zeeman broadening measurements, which reveal the distribution of magnetic field strengths with little dependence on the unknown field geometry (Robinson Jr, 1980; Saar, 1988; Valenti and Johns-Krull, 2001). Zeeman broadening is best measured for slowly rotating stars, in contrast to ZDI. Reliable measurements require Zeeman splitting larger than, or comparable to, line widths in the absence of the field. Zeeman splitting is proportional to the field strength B and effective Lande factor geff as
It is also proportional to the square of the wavelength. For this reason, successful measurements of magnetic field strengths can be carried out using red or IR lines with large geff. Also, only stars with strong magnetic fields and large field areas can be studied with this technique.
In order to derive magnetic field strength B and filling factor f, observed line profiles are fitted by the sum of synthetic spectra for magnetic and non-magnetic regions (Saar, 1994; Valenti and Johns-Krull, 2001):
Such an analysis implicitly assumes that (i) the field is concentrated into flux tubes surrounded by field free regions; (ii) flux tubes are oriented radially in the photosphere; (iii) magnetic regions are distributed uniformly over the surface; (iv) magnetic regions are characterised by a single field strength, and (v) the temperature structure is the same for magnetic and non-magnetic atmosphere (Valenti and Johns-Krull, 2001). In this approach, the field strength being determined from the splitting is usually well constrained, but the filling factor depends on the unknown temperature structure of magnetic regions. In the case when the used spectral line becomes stronger in starspots, the filling factor can be overestimated, and vice versa. Rüedi et al. (1997) concluded that magnetic field strength and filling factor cannot be determined separately for moderately active stars with optical spectra of spectral resolution less than 100000 and S/N≤250.
Magnetic field measurements for active dwarfs and giants are collected in Table 6 and are plotted in Figures 8 and 9 versus the photosphere temperature and filling factor, respectively. These plots indicate a tendency for cooler dwarfs to have stronger magnetic fields and larger areas covered by them. It is interesting that there is a clear contradiction between spot filling factors measured from light curves and magnetic field filling factors measured from spectral lines (see Figure 10). This contradiction suggests that the two filling factors refer to different activity signatures, such as spot umbra and penumbra, or even faculae. The latter, being brighter and possessing relatively strong magnetic fields, would indeed be better seen in atomic lines. This is also supported by results obtained with the ZDI technique, which reveals stronger magnetic fields for intermediate brightness regions (e.g., Donati and Collier Cameron, 1997). Thus, it appears that umbral magnetic fields have not been measured as yet.
Magnetic field measurements for active dwarfs (circles) and giants (squares) versus the photosphere temperature. Big circles indicate the sunspot umbra (B = 3 kG) and penumbra (B = 1.5 kG). The thick solid line is a linear fit to the data, excluding the sunspot umbra (based on data in Table 6).
Magnetic field measurements for active dwarfs (circles) and giants (squares) versus the filling factor. Big circles indicate the sunspot umbra (B = 3 kG) and penumbra (B = 1.5 kG). The thick solid line is a linear fit to the data, excluding the sunspot umbra (based on data in Table 6).
Filling factors of spots (open symbols) and magnetic fields (filled symbols) on the surfaces of active dwarfs (circles) and giants (squares) versus the photosphere temperature. The thick solid line is a polynomial fit to the spot filling factors. The dashed line is a fit to the magnetic field filling factor, excluding the Sun. A big circle emphasises the sunspot umbra (f ∼ 1%) (based on data in Tables 5 and 6).
In order to detect magnetic fields in the starspot umbra it is necessary to employ spectral lines that are very weak outside spots. Zeeman sensitive molecular lines are the lines of choice for this purpose (Berdyugina, 2002; see Figure 5).
5.3 Lifetimes
Lifetimes of starspots can be determined from long-term observations which are, for instance, provided by continuous photometric data. Hall and Henry (1994) analysed several dozen spotted stars and concluded that lifetimes of relatively small spots are proportional to their sizes, which is consistent with sunspot properties. Lifetimes of relatively large spots are possibly limited by a shear of surface differential rotation. On the other hand, large spots causing prominent light curve minima apparently can survive for many years, despite differential rotation, and form centres of activity, or active longitudes (see Section 5.4). This may even be true for pre-main-sequence stars. For instance, based on a comparison of the Doppler image with photometric spot models, Hatzes (1995) suggested that the spot on V410 Tau has survived on the stellar surface for about 20 yr. Doppler images suggest, however, that these regions often consist of several smaller spots. Lifetimes of those spots are yet to be analysed.
5.4 Active longitudes
Decades of continuous photometric monitoring of RS CVn stars revealed that large spots maintained their identities for years which was interpreted as a signature of one or two active longitudes similar to the distribution of solar energetic flares (Zeilik et al., 1988; Olah et al., 1988; Henry et al., 1995; Jetsu, 1996). Whether such a structure has a preferred orientation with respect to the line of centres in a binary, and how long it survives, was a long debate (Hall, 1996). Berdyugina and Tuominen (1998) showed that active longitudes on RS CVns are permanent but can continuously migrate in the orbital reference frame, and generally have no preferred orientation. The active longitudes are separated by 180° on average and differ in their activity level. Periodic switching of the dominant activity from one active longitude to the other results in a so-called flip-flop cycle (Berdyugina and Tuominen, 1998) which is described in more detail in Section 6.2. A further analysis of photometric data confirmed the existence of active longitudes on RS CVn stars (Lanza et al., 1998a; Rodonò et al., 2000).
Two active longitudes seem to be a conspicuous pattern of the stellar activity. In addition to RS CVn stars they have been found in the spot distribution on FK Com-type stars (Jetsu et al., 1993, 1999; Korhonen et al., 2002) and very active young solar analogues (Berdyugina et al., 2002; Järvinen et al., 2005b; Berdyugina and Järvinen, 2005). Two examples for the RS CVn star σ Gem and young dwarf AB Dor are shown in Figure 11.
Active longitudes, flip-flops, and sunspot-like cycles on the RS CVn star σ Gem (Berdyugina and Henry, 2005), young solar analogue AB Dor (Järvinen et al., 2005b), and the Sun (Berdyugina and Usoskin, 2003). The three plots upper panels show phases of spot concentrations (filled and open circles denote primary and secondary regions, respectively). The migration paths of active longitudes are emphasised by solid lines. Flip-flops are marked by vertical dashed lines. They occur when the primary region jumps to the opposite active longitude. For the Sun, only half-year average phases are shown and a linear drift of the active longitudes in the Carrington system is subtracted for better visibility. Lower panels in the plots show variations of the stellar brightness and sunspot area. Note that minimum brightness corresponds to maximum spotted area for both σ Gem and AB Dor, in contrast to the Sun (e.g., Amado et al., 2001).
The migration of active longitudes occurs with respect to the chosen reference frame. In binaries, this is usually the orbital ephemeris, while in single stars it represents an average epoch obtained over several years. If the migration is linear, a phase difference accumulates due to a constant difference between the assumed and true periods of the spot rotation. This is more common for binary components of RS CVn-type stars (Berdyugina and Tuominen, 1998). A nonlinear migration suggests the presence of differential rotation and changes in mean spot latitudes as, e.g., on the Sun. Such a behaviour is typical for single stars, young solar type dwarfs, and FK Com-type giants (see Figure 11).
The analogy with solar active longitudes is further supported by the longitudinal distribution of sunspots (Berdyugina and Usoskin, 2003). Large sunspot groups in both Northern and Southern hemispheres are preferably formed around two active longitudes which are separated by 180° and persistent for at least 120 yr. Similar to young solar-type dwarfs, the two active longitudes on the Sun are long-lived quasi-rigid structures which are not fixed in any reference frame due to differential rotation. They continuously migrate, with a variable rate, with respect to the chosen reference frame (see Figure 11). In the Carrington system, the migration results in a phase lag of about 2.5 solar rotations per sunspot cycle. The migration of active longitudes is caused by changes in the mean latitude of the sunspot formation and differential rotation. Sunspots are first formed at higher latitudes and approach the equator as the solar cycle advances. In the Carrington reference frame the migration is more rapid at the beginning of the cycle and slows down towards the end. The migration pattern of the active longitudes bears, therefore, the information on both differential rotation and mean spot latitudes. This can be used for inferring stellar differential rotation and butterfly diagrams.
5.5 Differential rotation
Differential rotation of stars plays an important role in the generation of magnetic fields in the convection zone. In the Sun, it is involved in transformation of a weak large-scale poloidal field into a stronger toroidal component. By analogy, stellar activity is most probably also connected to differential rotation.
On the Sun the differential rotation is observed in relative motion of sunspots and can be expressed in the form
where ψ denotes heliographic latitude, Ω0 is the rotation rate at the equator, and ΔΩ is the difference in rotation rate between the pole and the equator. A strength of the differential rotation can be quantified by the rotational shear ΔΩ or its reciprocal 2π/ΔΩ, which is the time the equatorial regions need to lap the pole, i.e., the lap time. It can also be characterised by the relative differential rotation rate which is expressed as the ratio of the rotational shear to the equatorial velocity
For instance, on the Sun with ΔΩ = 0.055 rad d−1, the lap time is 115 d, and α = 0.2.
On stars these characteristics can be estimated from observations with various methods, for instance: Fourier analysis of light curves (Lanza et al., 1993), cross-correlation of successive stellar Doppler images (Donati and Collier Cameron, 1997), direct spot tracking (Collier Cameron et al., 2002), Fourier transform of rotationally broadened line profiles (Reiners and Schmitt, 2002), parameter fit in Zeeman-Doppler imaging (Petit et al., 2002), through asteroseismology (Gizon and Solanki, 2004) and from spectro-interferometric observations (de Souza et al., 2004). For slowly rotating stars of the solar type, analysis of disk-integrated Ca ii K line core emission appears to be a promising method (Donahue et al., 1996; Hempelmann and Donahue, 1997).
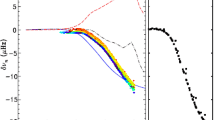
Long-term photometric monitoring of starspot modulation reveals changes in the seasonal rotation period which indicate the presence of differential rotation on stellar surfaces and of changes in spot latitudes (Hall, 1991a; Henry et al., 1995; Messina and Guinan, 2003). Confronting the range of seasonal variations and the mean rotation period yields a possible correlation between them in the sense that slower rotators show larger period variations. A majority of stars show, however, a significantly smaller rotational shear than that observed on the Sun. Similar behaviour is found in periods obtained from variations of chromospheric Ca ii H & K emission-line fluxes. Over timescales of many years, the rotation period was found to show a sine-like variation which can be attributed to a solar-type activity cycle (Donahue et al., 1996). Note, however, that the seasonal period variations yield only lower limits of the rotational shear as they represent rotational rates spread over the range of latitudes where active regions erupt during the stellar cycle.
Using the Fourier transform method Reiners and Schmitt (2003a,b) derived differential rotation in terms of α of a sample of rapidly rotating F0–G0 dwarfs and found that it is more common in slower rotators, in agreement with the previous findings. Moreover, the differential rotation in more active stars seems to diminish to values which cannot be measured with the Fourier transform technique.
In such cases, cross-correlation of successive stellar Doppler images is a helpful alternative. It was first performed by Donati and Collier Cameron (1997) for the active young dwarf AB Dor and revealed the solar type differential rotation with the equator rotating faster than the polar region (see Figure 12). The parameter fit using DI or ZDI developed by Donati et al. (2000) and Petit et al. (2002) is the next step in using inversion techniques. It was applied to a small sample of active G2–M2 dwarfs, all showing a solar type differential rotation (Petit et al., 2004; Barnes et al., 2005). This sample revealed a clear dependence of the rotational shear on spectral class, indicating the differential rotation to be negligible in M dwarfs and very strong in G dwarfs. The Sun, however, deviates from the correlation. In contrast to the results for early F and G dwarfs, no significant dependence of ΔΩ on rotation rate was found. An interesting finding though is that the differential rotation is different when estimated from cool spots or magnetic regions, and that it undergoes temporal fluctuations on time-scales of one to a few years (Donati et al., 2003a). Note, however, that the lack of spatial resolution and spot growth and decay as well as their systematic proper motions, can significantly affect the derived values of the differential rotation. Also, since spot latitudes strongly depend on the inclination of the rotational axis (see Section 4.2), uncertainties in the inclination may result in systematic errors in the deduced differential rotation law.
Two Doppler images of the young active K0 dwarf AB Dor (on the left) and a cross-correlation image (on the right) showing that near-equatorial spots rotate faster than high-latitude regions. From Donati and Collier Cameron (1997). See also animation by J.-F. Donati at http://webast.ast.obs-mip.fr/people/donati/diffrot2.html
5.6 Latitudes and butterfly diagrams
Spot latitudes can be directly recovered from Doppler images. Interesting and still controversial features in stellar Doppler images are large polar spots, cool active regions over the stellar poles. Out of 65 stars, whose surfaces were mapped with the Doppler imaging technique, 36 showed prominent polar spots, independently on the rotational rate or effective temperature (Strassmeier, 2002). Earlier studies, however, suggested that latitudinal distribution of spot activity may depend on the rotational period, since faster rotators apparently show a tendency for polar spots, while slower rotators more often have high-latitude spots not covering the pole (Hatzes, 1998). Such a feature appears to be a convenient compensation for a uniformly distributed spot area which cannot be recovered from rotational modulation of spectral lines and of light curves. On the other hand, flat-bottomed spectral line profiles in rapid rotators may indicate a lack of the continuum flux at the polar region, and this kind of profiles appears to be common for stars with a lower inclination of the rotational axis, implying changes of spot visibility near the poles (Hatzes et al., 1996).
The reliability of polar spots has been thoroughly discussed (Strassmeier et al., 1991; Schüssler and Solanki, 1992; Piskunov and Wehlau, 1994; Strassmeier and Rice, 1998). For instance, the chromospheric activity could reduce absorption in cores of strong spectral lines which can be interpreted as presence of cool polar caps. To investigate such a bias in Doppler imaging Unruh and Collier Cameron (1997) used Na D lines which are sensitive to the chromospheric temperature structure and found that the images obtained from the Na D lines show less high-latitude structure and give more reliable light-curve predictions than images derived previously from fits to several weaker photospheric lines. Also, Bruls et al. (1998) studied effects of the chromospheric temperature increase on spectral line profiles, including non-LTE effects. They concluded that it is unlikely that polar spots are an artefact due to unaccounted chromospheric activity. It appears that Doppler imaging using simultaneous inversions of atomic and molecular lines can limit the amount of non-modulating spot area and resolve the controversy of polar spots (Berdyugina, 2002).
In very active stars spots are distributed over a large range of latitudes, including low- and high-latitude spots, as shown by Doppler imaging and eclipse mapping models (Donati et al., 1999; Strassmeier et al., 1999; Berdyugina et al., 1998a, 1999a; Rodonò et al., 1995). A long-term Doppler imaging monitoring of the active component of HR 1099 suggests that starspots form at low or intermediate latitudes and then slowly migrate towards the pole on time scales of a few years (Vogt et al., 1999). Further evidence of poleward spot migration, based on more densely-sampled time-series imaging, was provided by Strassmeier and Bartus (2000).
The time span of Doppler images for most studied stars is not long enough to see the latitude changes over the spot cycle, i.e., to recover stellar butterfly diagrams. Light curve modelling offers a longer time scale but spot latitudes obtained from the model are usually not unique and, thus, are less reliable.
A new approach for recovering stellar butterfly diagrams was suggested by Berdyugina (2005). As was emphasised in Section 5.4, phase migration of the active longitudes bears the information on both differential rotation and mean spot latitudes. Thus, knowing the surface differential rotation and phase migration of active longitudes one can recover mean spot latitudes during the course of sunspot-like cycles. For young dwarfs the butterfly diagrams are reminiscent of the solar case, although the limited amount of collected results does not yet allow for any conclusions.
6 Starspot Evolution and Stellar Activity Cycles
6.1 Overall activity variations
Chromospheric plages produce flux variations in the emission cores of Ca ii H & K lines as observed on the Sun and Sun-like stars. Monitoring Ca ii emission on solar-type dwarfs, pioneered by O. Wilson at Mt. Wilson Observatory, has led to the detection of solar-like activity cycles in such stars (Baliunas et al., 1995). For a sample of stars (about 100) of spectral type G0-K5 V changes in rotation and chromospheric activity are found to occur on an evolutionary timescale. Young rapidly rotating stars exhibit high average levels of activity and rarely display a smooth, cyclic variation. Stars of intermediate age (approximately 1–2 Gyr for 1M⊙) have moderate levels of activity and occasional smooth cycles (see Figure 13). Finally, stars as old as the Sun and older have slower rotation rates, lower activity levels and smooth cycles. Some stars showed no variations at all, which was first interpreted as stars being in the stage similar to the Maunder minimum on the Sun. Later it was shown though that these stars are probably subgiants evolved off the main-sequence (Wright, 2004). In addition, contemporaneous photometric and chromospheric H & K emission time series for 35 stars revealed that the luminosity variation of young stars anti-correlates with their variation in chromospheric emission (Radick et al., 1998), i.e., young stars become fainter near their activity maxima, while older stars, including the Sun, become brighter at maximum activity. This suggests a shift from spot-dominated to faculae-dominated activity as stars evolve along the main-sequence. Such an evolution implies that activity cycles on young stars should be more prominent in spot patterns rather than in chromospheric plages.
Chromospheric Ca ii emission cycles for Sun-like stars, illustrating the regular cyclic variation that is common in such stars. The Ca ii emission is plotted in Mount Wilson “S-Index” units. From Radick (2000).
The detection of activity cycles in overall brightness variations due to cool spots on young solar analogues confirms the above implication. At least eight young dwarfs of the solar type and one weak-line T Tau star clearly show spot cycles (Amado et al., 2001; Berdyugina et al., 2002; Messina and Guinan, 2002, 2003; Stelzer et al., 2003; Järvinen et al., 2005b; Berdyugina and Järvinen, 2005). Two examples (AB Dor and LQ Hya) are shown in Figure 14. In contrast to the Sun, where the maximum spot area is reached at the maximum irradiance, on more active stars it occurs at minimum brightness. In addition, such stars exhibit periodic changes of spot rotation periods in phase with the spot cycle, which is consistent with the presence of a differential rotation. The latter may also vary with a cycle (Collier Cameron and Donati, 2002; Donati et al., 2003a). Variations of the total spottedness are also found on other types of cool active stars, including components of binary systems (e.g., Henry et al., 1995; see plot for σ Gem in Figure 14). The stellar spot cycles are, therefore, reminiscent of the 11-yr sunspot cycle.
A sample of stars with different rotation rates and cycle frequencies provides an opportunity to investigate the likely evolution of the stellar dynamo, as was done by, e.g., Saar and Brandenburg (1999). For instance, it appears that there is only a weak correlation, if any, between cycle and rotational frequencies, while the cycle length probably correlates with the differential rotation shear (Messina and Guinan, 2003). However, in such an analysis it is important to distinguish between different cycle types as they can be associated with different dynamo modes, as discussed by Moss (2004) and Fluri and Berdyugina (2004).
A comparison of the activity patterns of the present Sun and young solar analogues allows us to infer possible evolution of the stellar dynamo on main-sequence stars. First of all, the overall activity level is reducing while the star evolves along the main-sequence and looses its angular momentum. Secondly, the activity is changing from spot-dominated to faculae-dominated. This implies that cycles on young stars are more prominent in spot patterns, while on stars of the solar age cycles become more apparent in chromospheric plages. Thirdly, young stars show conspicuous non-axisymmetric fields, which weaken on the Sun and solar-age stars and coexist with a strong axisymmetric component.
6.2 Flip-flop cycles
Although active longitudes endure for a long time, the active regions they consist of evolve in size, indicating possible cyclic variations as observed in Doppler images (Berdyugina et al., 1998a, 1999a). While one active longitude reduces its activity level, the other increases, which suggests a redistribution of the spotted area between the opposite hemispheres (see Figure 15). When the active longitudes have about the same activity level a switch of the dominant activity from one longitude to the opposite one occurs. Such a phenomenon was first observed on FK Com (Jetsu et al., 1991) and was tentatively called flip-flop. Berdyugina and Tuominen (1998) have analysed long time series of photometric data for four RS CVn stars and discovered that flip-flops are regularly repeated and, thus, indicate a new type of stellar cycle which is related to active longitudes, i.e., a flip-flop cycle. Korhonen et al. (2002) inferred a flip-flop cycle on FK Com. In addition to RS CVn stars and FK Com, such cycles have been detected on young solar analogues (Berdyugina et al., 2002; Järvinen et al., 2005b; Berdyugina and Järvinen, 2005), examples of which are shown in Figure 11. A list of stars exhibiting a flip-flop phenomenon is given in Table 4
Doppler images of the RS CVn star II Peg in the pole-on projection illustrating a flip-flop that occurred between the end of 1997 and mid of 1998. From Berdyugina et al. (1999a).
The frequency ratio between the spot cycle and flip-flop cycle appears to be different for binary components and single stars. In RS CVn-type stars exhibiting both types of cycles, flip-flops appear to occur at the frequency of the spot cycle, implying the flip-flop cycle to be twice as long as the spot cycle. In young dwarfs flip-flop cycles are 3–4 times shorter than the spot cycle.
The solar active longitudes also exhibit a flip-flop cycle. On the Sun major spot activity alternates the active longitudes in about 1–3 yr, which results in flip-flop cycles of 3.8 and 3.65 yr in the northern and southern hemispheres, respectively (Berdyugina and Usoskin, 2003). This is about 1/3 of the 11-yr sunspot cycle and agrees with the results obtained for young solar analogues. The difference between flip-flop cycle lengths in the north and south is significant and produces an oscillating effect in the north-south asymmetry on a century time scale.
6.3 Orbital period modulation
A modulation of the orbital period in close binaries with cool active components is a phenomenon which is suggested to be associated with magnetic activity cycles (Hall, 1989). It can be induced by changes of the angular momentum and magnetic field distribution within the convection envelope of the active component, which may occur during an activity cycle (Applegate, 1992; Lanza et al., 1998b). The variation of the gravitational quadrupole momentum induces changes of the gravitational acceleration of the companion star, leading to the observed modulation of the orbital period. Possible variations of the stellar differential rotation may also be a manifestation of this mechanism (Collier Cameron and Donati, 2002; Donati et al., 2003a).
The time scale for such a modulation is of several decades and its cyclic origin is still an assumption. The relationship between the orbital period modulation and the starspot cycle is not yet clear. In some stars the spot cycle is half as long as the orbital period modulation (Keskin et al., 1994; Rodonò et al., 1995; Lanza et al., 1998a), in others these two cycles are approximately of the same length (Ibanoglu et al., 1994; Hall, 1991b). On the other hand, the length of the cycle of the orbital period modulation seems to be correlated with the angular velocity of the star. This supports the suggestion that a distributed non-linear dynamo is at work in the convection envelopes of very active stars and that it strongly affects the differential rotation (Lanza and Rodonò, 1999b). If the cyclic origin of the orbital period modulation and its relation to the spot cycle is confirmed, this can be used as a proxy for magnetic cycles in Algols and cataclysmic variables where photometric modulation of the cool secondary is difficult to detect.
7 Theoretical Models
7.1 Dynamo models
Mean field dynamo models assume a dynamo action which is extended over the entire convection envelope. In the Sun, a shell dynamo based on the αΩ mechanism seems to be able to explain the main features of the 11-yr cycle. However, in the most active stars it is difficult to reproduce the observed latitudinal range of starspots with the thin-shell dynamo models. It appears that in addition to a solar-like dynamo, probably working in the overshoot zone, a distributed α2Ω dynamo is likely to be present in very active stars (Brandenburg et al., 1989; Moss et al., 1995). Such a distributed dynamo is able to explain, at least qualitatively, a threshold for light modulation, active longitudes and flip-flops (see below). Also, it is a good candidate for explaining the observed orbital period modulation in active close binaries (Lanza et al., 1998b).
The geometry and behaviour of solar and stellar magnetic fields are globally determined by the stability of dynamo modes with different symmetry (Brandenburg et al., 1989). For instance, the sunspot cycle can be explained by an axisymmetric mean-field dynamo mode of \({\cal A}0\) type, which is antisymmetric with respect to the equator (dipole-like). Similarly, spot cycles in other stars can be also associated with an axisymmetric mode of \({\cal S}0\) type which is symmetric with respect to the equator (quadrupole-like).
Persistent active longitudes separated by 180° on the Sun and cool active stars clearly indicate the presence of non-axisymmetric dynamo modes. They can be either symmetric with respect to the equatorial plane, e.g., a dipole-like \({\cal S}1\) mode (Moss et al., 1991, 1995), or antisymmetric such as a quadrupole-like \({\cal A}1\) mode (Tuominen et al., 2002). The magnetic field configuration in such modes consists of magnetic spots of opposite polarities (active longitudes) 180° apart. It appears that such modes can be excited at lower dynamo numbers than axisymmetric modes in the case when the differential rotation is not large. The extention of these models to synchronised binaries reveals that the maxima of the mean magnetic field appears to concentrate near the line joining the centres of the binary components (Moss and Tuominen, 1997).
Beside the symmetry of the modes, their oscillatory properties are important. The mean-field dynamo theory favours oscillating axisymmetric modes with a clear cyclic behaviour and sign changes (as in the sunspot cycle), while non-axisymmetric modes appear to be rather steady.
The alternating active longitudes and flip-flop cycles observed on the Sun and other active stars imply, however, the existence of apparently oscillating non-axisymmetric fields. As is suggested by Berdyugina et al. (2002), perhaps the coexistence of oscillating axisymmetric and steady non-axisymmetric modes results in the appearance of flip-flop cycles. Then, the relative strengths of the two dynamo modes and the period of the oscillations of the axisymmetric mode should define the amplitudes and lengths of observed cycles. The possibility of such a mechanism was first demonstrated by the mean-field dynamo calculation of Moss (2004) who obtained a stable solution with an oscillating \({\cal S}0\) type mode and a steady, mixed-polarity non-axisymmetric mode. In this case flip-flops are quasi-periodic and as frequent as sign changes of the \({\cal S}0\) mode, which is reminiscent of the behaviour observed in some RS CVn stars. A similar mechanism involving an oscillating \({\cal A}0\) mode and a steady \({\cal S}1\) mode is discussed by Fluri and Berdyugina (2004).
More frequent flip-flops, compared to the sunspot-like cycle in single stars and the Sun, suggest a more complex field configuration. As shown by Fluri and Berdyugina (2004) flip-flops could also occur due to alternation of relative strengths of non-axisymmetric \({\cal S}1\) and \({\cal A}1\) modes without sign changes of any involved modes. If in addition a co-existing axisymmetric mode were changing its sign with a different frequency, it would result in the behaviour observed in solar-type stars. The stability of such a solution should however be tested by dynamo calculations.
Differential rotation is a key parameter for stellar dynamos, and a theoretical study of its dependence on the rotation rate and spectral type is important for interpreting observations. A noticeable progress in such modelling was achieved during the recent decade (Kitchatinov and Rüdiger, 1995; Rüdiger et al., 1998). In particular, the following results are important. Simulations of global circulation in outer stellar convection zones for spectral classes G2 and K5, rotating at the same rate, demonstrate that differential rotation for G2 is larger compared to K5 (Kitchatinov and Rüdiger, 1999). However, as the rotation period decreases, the differential rotation first decreases as well but starts to increase for the shortest periods. It appears that rapid rotation can explain the rather strong total surface differential rotation of the observed very young solar-type stars, as it creates an equatorward meridional flow at the stellar surface which accelerates the equatorial rotation (Rüdiger and Küker, 2002). A possibility for stars to have an anti-solar differential rotation was discussed by Kitchatinov and Rüdiger (2004).
The latest developments in the solar and stellar dynamo theory are reviewed by Brandenburg and Dobler (2002) and Rüdiger and Hollerbach (2004).
7.2 Flux-tube models
High-latitude spots on very active stars can be explained by non-linear models for flux-tube instability (Schüssler and Solanki, 1992; Schüssler et al., 1996). In a rapid rotator with a dynamo operating near the base of the convection zone, the effect of the Coriolis force makes flux tubes to emerge nearly parallel to the rotation axis, thus producing high-latitude activity even if the dynamo amplifies the field only at low latitudes. Such a model is capable to reproduce the sunspot behaviour as well (Caligari et al., 1995). In addition to rapid rotation, the depth of the convection zone, stratification and magnetic field strength play an equally important role in the poleward deflection of rising flux-tubes. In particular, the size of the stellar core affects the magnetic curvature force and the rise time, while gravity determines the strength of the buoyancy force.
Calculations for zero-age main-sequence stars show that for increasing rotation rate the emergence pattern shifts to higher latitudes, while an equatorial zone of avoidance grows (Granzer et al., 2000). The concentration to higher latitudes is stronger for stars with lower mass and deeper convection zones because of geometrical reasons and the larger rise time. It is remarkable that once the Coriolis effect has enforced a nearly axis-parallel rise of the flux tube, further increase of the rotation rate has no effect on the emergence latitudes, indicating a saturation effect. Truly polar flux emergence was, however, not found for main-sequence stars. Also, low-latitude activity in rapid rotators cannot be described by such a model. For T Tauri-type stars Granzer et al. (2000) find a different pattern of behaviour. Because of the small size of the stellar core, the unstable flux tubes detach completely from the overshoot layer and rise through the convection zone as free-floating rings. They can emerge in a broad range of latitudes, almost from pole to equator.
A similar perturbation study of rising flux-tubes have been made for close synchronised binary stars with main-sequence components in order to examine an influence of tidal effects on the formation of observed active longitudes (Holzwarth and Schüssler, 2003a, 2003b). It was found that although the magnitude of tidal effects is rather small, they nevertheless lead to the formation of clusters of flux tube eruptions at preferred longitudes on opposite sides of the star. The longitude distribution of the clusters depends on the initial parameters of flux-tubes in the overshoot region, such as magnetic field strength and latitude. This implies that there is no preferred orientation of the active longitudes and agrees with most of the observations. The extention of the model to post-main-sequence stars revealed difficulties in recovering starspot properties frequently observed on evolved binary components (Holzwarth, 2004). This points out an insufficiency of the applied flux tube model and implies that additional flux transport and possibly amplification mechanisms have to be taken into account.
Note that the flux-tube concept, when applied to heavily spotted stars, implicitly assumes that large starspots represent clusters of smaller, more sunspot-like magnetic structures, to which the thin flux-tube approximation is applicable during most of their rise through the convection zone (Schüssler, 2002). Further, such an approach gives only the information about potential emergence locations. The actual prediction of emergence patterns would require a coupling of the emergence calculations with a full dynamo model providing the flux distribution as functions of latitude, longitude and time.
8 Summary
Cool stars with external convection envelopes exhibit various magnetic phenomena similar to those observed on the Sun. Starspots are the best studied proxy of stellar magnetism and, thus, represent a key tool for understanding the stellar dynamo. A remarkable progress in observational facilities and numerical techniques for studying starspots achieved for the last two decades allows for a deep insight into the nature of starspots and underlying magnetic fields. In addition to traditional photometric and spectroscopic observations, advanced instrumentation for high-precision spectropolarimetry and (spectro-)interferometry together with foreseen space missions constitute a powerful arsenal for studying starspots and promise for ground-braking discoveries in stellar magnetism.
Starspot properties are revealed with the help of various numerical techniques, such as light-curve modelling and inversions, Doppler and Zeeman-Doppler imaging, molecular line diagnostics, asteroseismology, etc. Parallel brightness and colour variations, i.e., the faintest state being accompanied by the reddest colour, imply that starspots are significantly cooler than the unspotted photosphere, on average by 500 K to 2000 K. Large variations in brightness, up to 0.6 mag, indicate that the spotted areas are huge compared to that of sunspots, up to 30% of the whole stellar surface. Such large cool spots when passing over stellar disks cause strong line profile distortions in the spectra of rapidly rotating stars. Analysis of a time series of spectral line profile variations using Doppler imaging techniques provides the spot distribution over the visible stellar surface. Doppler images reveal that spots on cool rapidly rotating stars are preferably formed at higher latitudes, from 30° up to the visible pole, in contrast to sunspots which on average appear at latitudes below 30°. Magnetic field measurements suggest that the large starspots represent active regions consisting of smaller, mixed polarity spots.
Summarising the discussion on starspot evolution, the following main activity patterns appear to be common on cool active stars, namely components of binary systems, young single dwarfs and single rapidly rotating giants:
-
total spottedness variations indicating sunspot-like cycles;
-
persistent active longitudes 180° apart implying non-axisymmetric magnetic fields;
-
switching of dominant activity between active longitudes: flip-flop cycles;
-
migration of active longitudes;
-
differential rotation and butterfly diagrams;
-
orbital period variations in binaries: changes of the distribution of magnetic fields in the convection envelope.
Non-axisymmetric large-scale magnetic fields are persistent in various types of active stars including the Sun. Their continuous longitude migration implies the presence of differential rotation and provides an opportunity for studying stellar butterfly diagrams. Activity cycles revealed in variations of spot and plage area appear to accompany flip-flop cycles, i.e., periodic switching of dominant activity between opposite longitudes. An analysis of these phenomena can help to identify underlying dynamo modes.
These activity patterns challenge the current stellar dynamo theory. It appears that non-linear dynamo models can qualitatively explain most of the phenomena, although many parameters of the models are not realistic as yet.
Comparing the observed properties of the magnetic field on the Sun and active stars, we can conclude that the activity patterns emphasised above for single stars are also relevant for the solar case. There appears to be more similar between different types of stars than it was thought previously. Thus, fine details of the stellar dynamo can be deduced by studying the Sun, while its global parameters, on an evolutionary time scale, are provided by a sample of active stars.
9 Additional Tables
References
Abranin, E.P., Alekseev, I.Y., Avgoloupis, S., Bazelyan, L.L., Berdyugina, S.V., Cutispoto, G., Gershberg, R.E., Larionov, V.M., Leto, G., Lisachenko, V.N., Marino, G., Mavridis, L.N., Messina, S., Mel’nik, V.N., Pagano, I., Pustil’nik, S.V., Rodonò, M., Roizman, G.S., Seiradakis, J.H., Sigal, G.P., Shakhovskaya, N.I., Shakhovskoy, D.N., Shcherbakov, V.A., 1998, “Coordinated Observations of the Red Dwarf Flare Star EV LAC in 1994 and 1995”, Astron. Astrophys. Trans., 17, 221–262.
Alekseev, I.Y., Gershberg, R.E., 1996, “A model of zonal spottedness for red dwarf stars”, Astron. Zh., 40, 538–545.
Amado, P.J., Cutispoto, G., Lanza, A.F., Rodonò, M., 2001, “AB Doradus: Long and Short Term Light Variations and Spot Parameters”, in Cool Stars, Stellar Systems, and the Sun (11th Cambridge Workshop), (Eds.) García Lòpez, R.J., Rebolo, R., Zapaterio Osorio, M.R., Proceedings of a meeting held at Puerto de la Cruz, Tenerife, Spain, 4–8 October 1999, vol. 223 of ASP Conference Series, pp. 895–900, Astronomical Society of the Pacific, San Francisco, U.S.A.
Appenzeller, I., Dearborn, D.S.P., 1984, “Brightness variations caused by surface magnetic fields in pre-main-sequence stars”, Astrophys. J., 278, 689–694.
Appenzeller, I., Fricke, K., Furtig, W., Gassler, W., Hafner, R., Harkl, R., Hess, H.-J., Hummel, W., Jurgens, P., Kudritzki, R.-P., Mantel, K.-H., Meisl, W., Muschielok, B., Nicklas, H., Rupprecht, G., Seifert, W., Stahl, O., Szeifert, T., Tarantik, K., 1998, “Successful commissioning of FORS1 — the First Optical Instrument on the VLT”, Messenger, 94, 1–6.
Applegate, J.H., 1992, “A mechanism for orbital period modulation in close binaries”, Astrophys. J., 385, 621–629.
Baliunas, S.L., Donahue, R.A., Soon, W.H., Horne, J.H., Frazer, J., Woodard-Eklund, L., Bradford, M., Rao, L.M., Wilson, O.C., Zhang, Q., Bennett, W., Briggs, J., Carroll, S.M., Duncan, D.K., Figueroa, D., Lanning, H.H., Misch, A.A., Mueller, J., Noyes, R.W., Poppe, D., Porter, A.C., Robinson, C.R., Russell, J., Shelton, J.C., Soyumer, T., Vaughan, A.H., Whitney, J.H., 1995, “Chromospheric variations in main-sequence stars. II.”, Astrophys. J., 438, 269–287.
Barnes, J.R., Lister, T.A., Hilditch, R.W., Collier Cameron, A., 2004, “High-resolution Doppler images of the spotted contact binary AE Phe”, Mon. Not. R. Astron. Soc., 348, 1321–1331.
Barnes, J.R., Collier Cameron, A., Donati, J.-F., James, D.J., Marsden, S.C., Petit, P., 2005, “The dependence of differential rotation on temperature and rotation”, Mon. Not. R. Astron. Soc., 357, L1–L5.
Benedict, G.F., Nelan, E., McArthur, B., Story, D., van Altena, W., Ting-Gao, Y., Jefferys, W.H., Hemenway, P.D., Shelus, P.J., Whipple, A.L., Franz, O.G., Fredrick, L.W., Duncombe, R.L., 1993, “Periodic low-amplitude variations in the brightness of Proxima Centauri”, Publ. Astron. Soc. Pac., 105, 487–493.
Berdyugina, S.V., 1998, “Surface imaging by the Occamian approach. Basic principles, simulations, and tests”, Astron. Astrophys., 338, 97–105.
Berdyugina, S.V., 2002, “Sunspot and starspot interiors as seen from molecular lines”, Astron. Nachr., 323, 192–195.
Berdyugina, S.V., 2004, “Non-axisymmetric magnetic fields and flip-flops on the Sun and cool stars”, Solar Phys., 224, 123–131.
Berdyugina, S.V., 2005, “Stellar butterfly diagrams”, Astron. Astrophys., in preparation.
Berdyugina, S.V., Henry, G.W., 2005, “Active longitudes and flip-flops on RS CVn-type stars”, Astrophys. J., in preparation.
Berdyugina, S.V., Järvinen, S.P., 2005, “Spot activity cycles and flip-flops on young solar analogs”, Astron. Nachr., 326, 283–286.
Berdyugina, S.V., Solanki, S.K., 2002, “The molecular Zeeman effect and diagnostics of solar and stellar magnetic fields. I. Theoretical spectral patterns in the Zeeman regime”, Astron. Astrophys., 385, 701–715.
Berdyugina, S.V., Tuominen, I., 1998, “Permanent active longitudes and activity cycles on RS CVn stars”, Astron. Astrophys., 336, L25–L28.
Berdyugina, S.V., Usoskin, I.G., 2003, “Active longitudes in sunspot activity: Century scale persistence”, Astron. Astrophys., 405, 1121–1128.
Berdyugina, S.V., Berdyugin, A.V., Ilyin, I., Tuominen, I., 1998a, “The active RS Canum Venaticorum binary II Pegasi. II. Surface images for 1992–1996”, Astron. Astrophys., 340, 437–446.
Berdyugina, S.V., Jankov, S., Ilyin, I., Tuominen, I., Fekel, F.C., 1998b, “The active RS Canum Venaticorum binary II Pegasi. I. Stellar and orbital parameters”, Astron. Astrophys., 334, 863–872.
Berdyugina, S.V., Berdyugin, A.V., Ilyin, I., Tuominen, I., 1999a, “The active RS Canum Venaticorum binary II Pegasi. IV. The spot activity cycle”, Astron. Astrophys., 350, 626–634.
Berdyugina, S.V., Ilyin, I., Tuominen, I., 1999b, “The long-period RS Canum Venaticorum binary IM Pegasi. I. Orbital and stellar parameters”, Astron. Astrophys., 347, 932–936.
Berdyugina, S.V., Berdyugin, A.V., Ilyin, I., Tuominen, I., 2000, “The long-period RS CVn binary IM Pegasi. II. First surface images”, Astron. Astrophys., 360, 272–280.
Berdyugina, S.V., Pelt, J., Tuominen, I., 2002, “Magnetic activity in the young solar analog LQ Hydrae. I. Active longitudes and cycles”, Astron. Astrophys., 394, 505–515.
Berdyugina, S.V., Solanki, S.K., Frutiger, C., 2003, “The molecular Zeeman effect and diagnostics of solar and stellar magnetic fields. II. Synthetic Stokes profiles in the Zeeman regime”, Astron. Astrophys., 412, 513–527.
Bopp, B.W., 1981, “Observations of FK Comae stars”, in Second Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, (Eds.) Giampapa, M.S., Golub, L., vol. 392 of SAO Rep., pp. 207–217, SAO, Cambridge.
Bopp, B.W., Evans, D.S., 1973, “The spotted flare stars BY Dra and CC Eri: A model for the spots and some astrophysical implications”, Mon. Not. R. Astron. Soc., 164, 343–356.
Bopp, B.W., Rucinski, S.M., 1981, “The Rapidly Rotating Giants of the FK Comae Type”, in Fundamental Problems in the Theory of Stellar Evolution, (Eds.) Sugimoto, D., Lamb, D.G., Schramm, D.N., IAU Symposium 93, held at Kyoto University, Kyoto, Japan, July 22–25, 1980, p. 177, D. Reidel, Dordrecht, Netherlands; Boston, U.S.A.
Bopp, B.W., Stencel, R.E., 1981, “The FK Comae stars”, Astrophys. J., 247, L131–L134.
Bopp, B.W., Saar, S.H., Ambruster, C., Feldman, P., Dempsey, R.C., Allen, M., Barden, S.C., 1989, “The active chromosphere binary HD 17433 (VY Arietis)”, Astrophys. J., 339, 1059–1072.
Bouvier, J., Bertout, C., 1989, “Spots on T Tauri stars”, Astron. Astrophys., 211, 99–114.
Brandenburg, A., Dobler, W., 2002, “Solar and stellar dynamos — latest developments”, Astron. Nachr., 323, 411–416.
Brandenburg, A., Krause, F., Meinel, R., Moss, D., Tuominen, I., 1989, “The stability of nonlinear dynamos and the limited role of kinematic growth rates”, Astron. Astrophys., 213, 411–422.
Brown, S.F., Donati, J.-F., Rees, D.E., Semel, M., 1991, “Zeeman-Doppler imaging of active stars. IV — Maximum entropy reconstruction of 2D magnetic topologies”, Astron. Astrophys., 250, 463–474.
Bruls, J.H.M.J., Solanki, S.K., Schüssler, M., 1998, “Doppler imaging: the polar spot controversy”, Astron. Astrophys., 336, 231–241.
Budding, E., 1977, “The interpretation of cyclical photometric variations in certain dwarf Me-type stars”, Astrophys. Space Sci., 48, 207–223.
Caligari, P., Moreno-Insertis, F., Schüssler, M., 1995, “Emerging flux tubes in the solar convection zone. I. Asymmetry, tilt, and emergence latitude”, Astrophys. J., 441, 886–902.
Catalano, S., Biazzo, K., Frasca, A., Marilli, E., 2002, “Measuring starspot temperature from line depth ratios. I. The method”, Astron. Astrophys., 394, 1009–1021.
Chugainov, P.F., 1966, “On the Variability of HD 234677”, Inform. Bull. Var. Stars, 122, 1–2.
Chugainov, P.F., 1971, “On the Cause of Periodic Light Variations of Some Red Dwarf Stars”, Inform. Bull. Var. Stars, 520, 1–3.
Chugainov, P.F., 1976, “Estimates of spot area and temperature on BY Dra”, Krymskaia Astrofiz. Obs. Izv., 55, 94–99.
Collier Cameron, A., 1992, “Modelling Stellar Photospheric Spots Using Spectroscopy”, in Surface Inhomogeneities on Late-Type Stars, (Eds.) Byrne, P.B., Mullan, D.J., Proceedings of a colloquium held at Armagh Observatory, Northern Ireland, 24–27 July, 1990, vol. 397 of Lecture Notes in Physics, p. 33, Springer, Berlin, Germany; New York, U.S.A.
Collier Cameron, A., 1995, “New limits on starspot lifetimes for AB Doradus”, Mon. Not. R. Astron. Soc., 275, 534–544.
Collier Cameron, A., 1997, “Eclipse mapping of late-type close binary stars”, Mon. Not. R. Astron. Soc., 287, 556–566.
Collier Cameron, A., Donati, J.-F., 2002, “Doin’ the twist: secular changes in the surface differential rotation on AB Doradus”, Mon. Not. R. Astron. Soc., 329, L23–L27.
Collier Cameron, A., Donati, J.-F., Semel, M., 2002, “Stellar differential rotation from direct star-spot tracking”, Mon. Not. R. Astron. Soc., 330, 699–706.
de Souza, D., Zorec, J., Jankov, S., Vakili, F., Abe, L., Janot-Pacheco, E., 2004, “Stellar differential rotation and inclination angle from spectro-interferometry”, Astron. Astrophys., 418, 781–794.
Deutsch, A.J., 1958, “Harmonic Analysis of the Periodic Spectrum Variables”, in Electromagnetic Phenomena in Cosmical Physics, (Ed.) Lehnert, B., IAU Symposium no. 6, pp. 209–221, Cambridge University Press, Cambridge, U.K.
Donahue, R.A., Saar, S.H., Baliunas, S.L., 1996, “A Relationship between Mean Rotation Period in Lower Main-Sequence Stars and Its Observed Range”, Astrophys. J., 466, 384–391.
Donati, J.-F., Brown, S.F., 1997, “Zeeman-Doppler imaging of active stars. V. Sensitivity of maximum entropy magnetic maps to field orientation”, Astron. Astrophys., 326, 1135–1142.
Donati, J.-F., Collier Cameron, A., 1997, “Differential rotation and magnetic polarity patterns on AB Doradus”, Mon. Not. R. Astron. Soc., 291, 1–19.
Donati, J.-F., Semel, M., Praderie, F., 1989, “Zeeman-Doppler imaging of active stars. II — Numerical simulation and first observational results”, Astron. Astrophys., 225, 467–478.
Donati, J.-F., Semel, M., Carter, B.D., Rees, D.E., Collier Cameron, A., 1997, “Spectropolarimetric observations of active stars”, Mon. Not. R. Astron. Soc., 291, 658–682.
Donati, J.-F., Collier Cameron, A., Hussain, G.A.J., Semel, M., 1999, “Magnetic topology and prominence patterns on AB Doradus”, Mon. Not. R. Astron. Soc., 302, 437–456.
Donati, J.-F., Mengel, M., Carter, B.D., Marsden, S., Collier Cameron, A., Wichmann, R., 2000, “Surface differential rotation and prominences of the Lupus post T Tauri star RX J1508.6–4423”, Mon. Not. R. Astron. Soc., 316, 699–715.
Donati, J.-F., Collier Cameron, A., Petit, P., 2003a, “Temporal fluctuations in the differential rotation of cool active stars”, Mon. Not. R. Astron. Soc., 345, 1187–1199.
Donati, J.-F., Collier Cameron, A., Semel, M., Hussain, G.A.J., Petit, P., Carter, B.D., Marsden, S.C., Mengel, M., López Ariste, A., Jeffers, S.V., Rees, D.E., 2003b, “Dynamo processes and activity cycles of the active stars AB Doradus, LQ Hydrae and HR 1099”, Mon. Not. R. Astron. Soc., 345, 1145–1186.
Dorren, J.D., 1987, “A new formulation of the starspot model, and the consequences of starspot structure”, Astrophys. J., 320, 756–767.
Dorren, J.D., Guinan, E.F., 1982, “Evidence for starspots on single solar-like stars”, Astron. J., 87, 1546–1557.
Dorren, J.D., Guinan, E.F., 1994, “HD 129333: The Sun in its infancy”, Astrophys. J., 428, 805–818.
Drake, S.A., Simon, T., Linsky, J.L., 1989, “A survey of the radio continuum emission of RS Canum Venaticorum and related active binary systems”, Astrophys. J. Suppl. Ser., 71, 905–930.
Eaton, J.A., Hall, D.S., 1979, “Starspots as the cause of the intrinsic light variations in RS Canum Venaticorum type stars”, Astrophys. J., 227, 907–922.
Eggen, O.J., 1967, “Contact binaries. II”, Mem. R. Astron. Soc., 70, 111–164.
Fekel, F.C., Balachandran, S., 1993, “Lithium and rapid rotation in chromospherically active single giants”, Astrophys. J., 403, 708–721.
Fekel, F.C., Henry, G.W., 2005, “Chromospherically Active Stars. XXIV. The Giant, Single-Lined Binaries HD37824, HD181809, and HD217188”, Astron. J., 129, 1669–1685.
Fields, D.L., Albrow, M.D., An, J., Beaulieu, J.-P., Caldwell, J.A.R., DePoy, D.L., Dominik, M., Gaudi, B.S., Gould, A., Greenhill, J., Hill, K., Jorgensen, U.G., Kane, S., Martin, R., Menzies, J., Pogge, R.W., Pollard, K.R., Sackett, P.D., Sahu, K.C., Vermaak, P., Watson, R., Williams, A., Glicenstein, J.-F., Hauschildt, P.H., 2003, “High-Precision Limb-Darkening Measurement of a K3 Giant Using Microlensing”, Astrophys. J., 596, 1305–1319.
Fluri, D.M., Berdyugina, S.V., 2004, “Flip-flops as observational signatures of different dynamo modes in cool stars”, Solar Phys., 224, 153–160.
Frasca, A., Biazzo, K., Catalano, S., Marilli, E., Messina, S., Rodonò, M., 2005, “Measuring starspot temperature from line-depth ratios. II. Simultaneous modeling of light and temperature curves”, Astron. Astrophys., 432, 647–655.
Fröhlich, C., 2002, “Total solar irradiance variations since 1978”, Adv. Space Res., 29, 1409–1416.
Geppert, U., Rheinhardt, M., Gil, J., 2003, “Spot-like structures of neutron star surface magnetic fields”, Astron. Astrophys., 412, L33–L36.
Gershberg, R.E., 1982, “A hypothesis on the hydromagnetic activity of T Tau type stars and related objects”, Astron. Nachr., 303, 251–261.
Gizon, L., 2002, “Prospects for detecting stellar activity through asteroseismology”, Astron. Nachr., 323, 251–253.
Gizon, L., Solanki, S.K., 2004, “Measuring Stellar Differential rotation with asteroseismology”, Solar Phys., 220, 169–184.
Goncharskii, A.V., Stepanov, V.V., Khokhlova, V.L., Yagola, A.G., 1977, “Reconstruction of local line profiles from those observed in an Ap spectrum”, Sov. Astron. Lett., 3, 147–149.
Grankin, K.N., Ibragimov, M.A., Kondrat’ev, V.B., Mel’nikov, S.Y., Shevchenko, V.S., 1995, “Photometric study of the properties of spot rotational modulation in weak line T Tauri stars”, Astron. Zh., 39, 799–807.
Granzer, T., Schüssler, M., Caligari, P., Strassmeier, K.G., 2000, “Distribution of starspots on cool stars. II. Pre-main-sequence and ZAMS stars between 0.4 M⊙ and 1.7 M⊙”, Astron. Astrophys., 355, 1087–1097.
Gray, D.F., 1996, “The determination of temperature from spectral lines”, in Stellar Surface Structure, (Eds.) Strassmeier, K.G., Linsky, J.L., Proceedings of the 176th Symposium of the International Astronomical Union, held in Vienna, Austria, October 9–13, 1995, pp. 227–235, Kluwer, Dordrecht, Netherlands; Boston, U.S.A.
Güdel, M., Guinan, E.F., Skinner, S.L., 1997, “The X-Ray Sun in Time: A Study of the Long-Term Evolution of Coronae of Solar-Type Stars”, Astrophys. J., 483, 947–960.
Guenther, E.W., Ball, M., 1999, “A spectroscopic study of flares on T Tauri and zero-age main-sequence stars”, Astron. Astrophys., 347, 508–517.
Guinan, E.F., Robinson, C.R., 1986, “FK Comae — The kinematical determination of its age and evolutionary status”, Astron. J., 91, 935–939.
Guinan, E.F., Güdel, M., Kang, Y.W., Margheim, S., 1997, “Chromospherically Active Stars in the Galactic Bulge as the Source of the Diffuse X-Ray Background Emission”, in Variables Stars and the Astrophysical Returns of the Microlensing Surveys, (Eds.) Ferlet, R., Maillard, J.-P., Raban, B., Proceedings of the 12th IAP Astrophysics Meeting, July 8–12, 1996, Institut d’Astrophysique de Paris, p. 339, Editions Frontières, Gif-sur-Yvette, France.
Hall, D.S., 1976, “The RS CVn binaries and binaries with similar properties”, in Multiple Periodic Variable Stars, (Ed.) Fitch, W.S., Proceedings of the International Astronomical Union colloquium no. 29, held at Budapest, Hungary, 1–5 September 1975, p. 287, D. Reidel, Dordrecht, Netherlands; Boston, U.S.A.
Hall, D.S., 1989, “The relation between RS CVn and Algol”, Space Sci. Rev., 50, 219–233.
Hall, D.S., 1991a, “Learning about stellar dynamos from longterm photometry of starspots”, in The Sun and Cool Stars: Activity, Magnetism, Dynamos, (Eds.) Tuominen, I., Moss, D., Rüdiger, G., Proceedings of Colloquium no. 130 of the International Astronomical Union, held in Helsinki, Finland, 17–20 July 1990, vol. 380 of Lecture Notes in Physics, p. 353, Springer, Berlin, Germany; New York, U.S.A.
Hall, D.S., 1991b, “A connection between long-term luminosity variations and orbital period changes in chromospherically active binaries”, Astrophys. J., 380, L85–L87.
Hall, D.S., 1996, “What we don’t know about starspots”, in Stellar surface structure, (Eds.) Strassmeier, K.G., Linsky, J.L., Proceedings of the 176th Symposium of the International Astronomical Union, held in Vienna, Austria, October 9–13, 1995, pp. 217–226, Kluwer, Dordrecht, Netherlands; Boston, U.S.A.
Hall, D.S., Henry, G.W., 1994, “The Law of Starspot Lifetimes”, IAPPP Commun., 55, 51–57.
Hartmann, L., 1990, “Emission lines and winds from T Tauri stars”, in Cool Stars, Stellar Systems, and the Sun (Sixth Cambridge Workshop), (Ed.) Wallerstein, G., Proceedings of the workshop held in Seattle, WA, September 18–21, 1989, vol. 9 of ASP Conference Series, pp. 289–300, Astronomical Society of the Pacific, San Francisco, U.S.A.
Hatzes, A.P., 1995, “Doppler Imaging of the Cool Spot Distribution on the Weak T Tauri Star V410 Tauri”, Astrophys. J., 451, 784–794.
Hatzes, A.P., 1998, “Spot activity and the differential rotation on HD 106225 derived from Doppler tomography”, Astron. Astrophys., 330, 541–548.
Hatzes, A.P., Vogt, S.S., Ramseyer, T.F., Misch, A.A., 1996, “The inclination dependence of the mean spectral line shapes of RS CVn stars: Further evidence for polar spots”, Astrophys. J., 469, 808–818.
Hempelmann, A., Donahue, R.A., 1997, “Wavelet analysis of stellar differential rotation. I. The Sun”, Astron. Astrophys., 322, 835–840.
Hendry, M.A., Bryce, H.M., Valls-Gabaud, D., 2002, “The microlensing signatures of photospheric starspots”, Mon. Not. R. Astron. Soc., 335, 539–549.
Hendry, P.D., Mochnacki, S.W., 2000, “Doppler Imaging of VW Cephei: Distribution and Evolution of Starspots on a Contact Binary”, Astrophys. J., 531, 467–493.
Henry, G.W., Eaton, J.A., Hamer, J., Hall, D.S., 1995, “Starspot evolution, differential rotation, and magnetic cycles in the chromospherically active binaries λ Andromedae, σ Geminorum, II Pegasi, and V711 Tauri”, Astrophys. J. Suppl. Ser., 97, 513–549.
Heyrovský, D., Sasselov, D., 2000, “Detecting Stellar Spots by Gravitational Microlensing”, Astrophys. J., 529, 69–76.
Holzwarth, V., 2004, “Spot signatures of a solar-type dynamo in close binary stars”, Astron. Nachr., 325, 408–412.
Holzwarth, V., Schüssler, M., 2003a, “Dynamics of magnetic flux tubes in close binary stars. I. Equilibrium and stability properties”, Astron. Astrophys., 405, 291–301.
Holzwarth, V., Schüssler, M., 2003b, “Dynamics of magnetic flux tubes in close binary stars. II. Nonlinear evolution and surface distributions”, Astron. Astrophys., 405, 303–311.
Huenemoerder, D.P., Ramsey, L.W., 1987, “CCD Echelle observations of the active RS CVn system II Pegasi”, Astrophys. J., 319, 392–402.
Huenemoerder, D.P., Ramsey, L.W., Buzasi, D.L., 1989, “Titanium oxide variations in II Pegasi”, Astron. J., 98, 2264–2267.
Hussain, G.A.J., Donati, J.-F., Collier Cameron, A., Barnes, J.R., 2000, “Comparisons of images derived from independent Zeeman Doppler imaging codes”, Mon. Not. R. Astron. Soc., 318, 961–973.
Hussain, G.A.J., Jardine, M., Collier Cameron, A., 2001, “Mapping potential fields on the surfaces of rapidly rotating stars”, Mon. Not. R. Astron. Soc., 322, 681–688.
Ibanoglu, C., Keskin, V., Akan, M.C., Evren, S., Tunca, Z., 1994, “Long-term luminosity variations and period changes in V471 Tauri”, Astron. Astrophys., 281, 811–816.
Jankov, S., Foing, B.H., 1992, “Tomographic imaging of late-type stars from spectroscopic and photometric rotational modulation. I — Principle and mathematical formulation of the method”, Astron. Astrophys., 256, 533–550.
Jankov, S., Vakili, F., Domiciano de Souza Jr, A., Janot-Pacheco, E., 2001, “Interferometric-Doppler imaging of stellar surface structure”, Astron. Astrophys., 377, 721–734.
Jankov, S., Domiciano de Souza Jr, A., Stehloe, C., Vakili, F., Perraut-Rousselet, K., Chesneau, O., 2003, “Interferometric-Doppler imaging of stellar surface abundances”, in Interferometry for Optical Astronomy II, (Ed.) Traub, W.A., 22–28 August 2002, Waikoloa, Hawaii, USA, vol. 4838 of SPIE Proceedings, pp. 587–593, International Society for Optical Engineering, Bellingham, U.S.A.
Järvinen, S.P., Berdyugina, S.V., Strassmeier, K.G., 2005a, “Magnetic activity in the young solar analog EK Dra: Active longitudes and cycles from long-term photometry”, Astron. Astrophys., accepted.
Järvinen, S.P., Berdyugina, S.V., Tuominen, I., Cutispoto, G., Bos, M., 2005b, “Magnetic activity in the young solar analog AB Dor: Active longitudes and cycles from long-term photometry”, Astron. Astrophys., 432, 657–664.
Jetsu, L., 1996, “The active longitudes of λ Andromedae, σ Geminorum, II Pegasi and V 711 Tauri”, Astron. Astrophys., 314, 153–164.
Jetsu, L., Pelt, J., Tuominen, I., Nations, H., 1991, “The spot activity of FK Comae”, in The Sun and Cool Stars: Activity, Magnetism, Dynamos, (Eds.) Tuominen, I., Moss, D., Rüdiger, G., Proceedings of Colloquium no. 130 of the International Astronomical Union, held in Helsinki, Finland, 17–20 July 1990, vol. 380 of Lecture Notes in Physics, pp. 381–383, Springer, Berlin, Germany; New York, U.S.A.
Jetsu, L., Pelt, J., Tuominen, I., 1993, “Spot and flare activity of FK Comae Berenices: Long-term photometry”, Astron. Astrophys., 278, 449–462.
Jetsu, L., Pelt, J., Tuominen, I., 1999, “Time series analysis of V 1794 Cygni long-term photometry”, Astron. Astrophys., 351, 212–224.
Johns-Krull, C.M., Valenti, J.A., 1996, “Detection of Strong Magnetic Fields on M Dwarfs”, Astrophys. J. Lett., 459, L95–L98.
Johns-Krull, C.M., Valenti, J.A., Hatzes, A.P., Kanaan, A., 1999a, “Spectropolarimetry of Magnetospheric Accretion on the Classical T Tauri Star BP Tauri”, Astrophys. J., 510, L41–L44.
Johns-Krull, C.M., Valenti, J.A., Koresko, C., 1999b, “Measuring the Magnetic Field on the Classical T Tauri Star BP Tauri”, Astrophys. J., 516, 900–915.
Joy, A.H., 1945, “T Tauri Variable Stars.”, Astrophys. J., 102, 168–195.
Keskin, V., Ibanoglu, C., Akan, M.C., Evren, S., Tunca, Z., 1994, “Luminosity variations and orbital period changes in RT Lacertae”, Astron. Astrophys., 287, 817–823.
Kitchatinov, L.L., Rüdiger, G., 1995, “Differential rotation in solar-type stars: revisiting the Taylor-number puzzle”, Astron. Astrophys., 299, 446–452.
Kitchatinov, L.L., Rüdiger, G., 1999, “Differential rotation models for late-type dwarfs and giants”, Astron. Astrophys., 344, 911–917.
Kitchatinov, L.L., Rüdiger, G., 2004, “Anti-solar differential rotation”, Astron. Nachr., 325, 496–500.
Kiurkchieva, D.P., 1990, “Photometry of stars with nonhomogeneous temperature spots”, Astrophys. Space Sci., 172, 255–262.
Kochukhov, O., Piskunov, N.E., Valenti, J.A., Johns-Krull, C.M., 2001, “The Search and Modelling of Magnetic Fields on M Dwarfs”, in Magnetic Fields Across the Hertzsprung-Russell Diagram, (Eds.) Mathys, G., Solanki, S.K., Wickramasinghe, D.T., Proceedings of a workshop held in Santiago, Chile, 15–19 January 2001, vol. 248 of ASP Conference Series, pp. 219–222, Astronomical Society of the Pacific, San Francisco, U.S.A.
Königl, A., 1991, “Disk accretion onto magnetic T Tauri stars”, Astrophys. J., 370, L39–L43.
Korhonen, H., Berdyugina, S.V., Hackman, T., Duemmler, R., Ilyin, I.V., Tuominen, I., 1999, “Study of FK Comae Berenices. I. Surface images for 1994 and 1995”, Astron. Astrophys., 346, 101–110.
Korhonen, H., Berdyugina, S.V., Tuominen, I., 2002, “Study of FK Comae Berenices. IV. Active longitudes and the “flip-flop” phenomenon”, Astron. Astrophys., 390, 179–185.
Kron, G.E., 1947, “The probable detection of patches of varying brightness on AR Lacertae B”, Publ. Astron. Soc. Pac., 350, 261–265.
Kron, G.E., 1952, “A Photoelectric Study of the Dwarf M Eclipsing Variable YY Geminorum”, Astrophys. J., 115, 301–319.
Kürster, M., 1993, “Doppler imaging with a CLEAN-like approach. I. A newly developed algorithm simulations and tests”, Astron. Astrophys., 274, 851–869.
Lagarde, S., Sanchez, L.J., Petrov, R.G., 1995, “Sub-resolution Limit Spatio-Spectral Information Using Differential Speckle Interferometry”, in Tridimensional Optical Spectroscopic Methods in Astrophysics, (Eds.) Comte, G., Marcelin, M., Proceedings of I.A.U. Colloquium 149, Marseille (France), 22–25 March 1994, vol. 71 of ASP Conference Series, p. 360, Astronomical Society of the Pacific, San Francisco, U.S.A.
Landi Degl’Innocenti, E., 1976, “Are there spots on magnetic white dwarfs?”, Astrophys. J., 209, 208–213.
Lanza, A.F., Rodonò, M., 1999a, “Observations and modelling of starspots: A tool to understand stellar dynamos”, in Solar and Stellar Activity: Similarities and Differences, (Eds.) Butler, C.J., Doyle, J.G., Proceedings of a meeting held in Armagh, N. Ireland, 2–4 September 1998, vol. 158 of ASP Conference Series, pp. 121–132, Astronomical Society of the Pacific, San Francisco, U.S.A.
Lanza, A.F., Rodonò, M., 1999b, “Orbital period modulation and quadrupole moment changes in magnetically active close binaries”, Astron. Astrophys., 349, 887–897.
Lanza, A.F., Rodonò, M., 2002, “Asteroseismic tests for models of magnetically active close binaries with orbital period modulation”, Astron. Astrophys., 390, 167–172.
Lanza, A.F., Rodonò, M., Zappala, R.A., 1993, “Fourier analysis of spotted star light curves as a tool to detect stellar differential rotation”, Astron. Astrophys., 269, 351–354.
Lanza, A.F., Catalano, S., Cutispoto, G., Pagano, I., Rodonò, M., 1998a, “Long-term starspot evolution, activity cycle and orbital period variation of AR Lacertae”, Astron. Astrophys., 332, 541–560.
Lanza, A.F., Rodonò, M., Rosner, R., 1998b, “Orbital period modulation and magnetic cycles in close binaries”, Mon. Not. R. Astron. Soc., 296, 893–902.
Libbrecht, K.G., Woodard, M.F., 1990, “Solar-cycle effects on solar oscillation frequencies”, Nature, 345, 779–782.
Lockwood, G.W., Thompson, D.T., Radick, R.R., Osborn, W.H., Baggett, W.E., Duncan, D.K., Hartmann, L.W., 1984, “The photometric variability of solar-type stars. IV Detection of rotational modulation among Hyades stars”, Publ. Astron. Soc. Pac., 96, 714–722.
Maceroni, C., Vilhu, O., van’t Veer, F., van Hamme, W., 1994, “Surface imaging of late-type contact binaries. I. AE Phoenicis and YY Eridani”, Astron. Astrophys., 288, 529–537.
Marsden, S.C., Waite, I.A., Carter, B.D., Donati, J.-F., 2005, “Doppler imaging and surface differential rotation of young open cluster stars. I. HD307938 (R58) in IC 2602”, Mon. Not. R. Astron. Soc., 359, 711–724.
Maxted, P.F.L., Ferrario, L., Marsh, T.R., Wickramasinghe, D.T., 2000, “WD1953-011: a magnetic white dwarf with peculiar field structure”, Mon. Not. R. Astron. Soc., 315, L41–L44.
Mekkaden, M.V., 1985, “Rotation and Hα emission activity in F8–G3 dwarfs”, Astrophys. Space Sci., 117, 381–385.
Messina, S., Guinan, E.F., 2002, “Magnetic activity of six young solar analogues I. Starspot cycles from long-term photometry”, Astron. Astrophys., 393, 225.
Messina, S., Guinan, E.F., 2003, “Magnetic activity of six young solar analogues II. Surface differential rotation from long-term photometry”, Astron. Astrophys., 409, 1017–1030.
Messina, S., Guinan, E.F., Lanza, A.F., 1999, “Photospheric Magnetic Activity in a Proxy for the Young Sun: HD 134319”, Astrophys. Space Sci., 260, 493–505.
Middelkoop, F., 1981, “Magnetic structure in cool stars. III — CA II H and K emission and rotation of main-sequence stars”, Astron. Astrophys., 101, 295–298.
Moss, D., 2004, “Dynamo models and the flip-flop phenomenon in late-type stars”, Mon. Not. R. Astron. Soc., 352, L17–L20.
Moss, D., Tuominen, I., 1997, “Magnetic field generation in close binary systems”, Astron. Astrophys., 321, 151–158.
Moss, D., Brandenburg, A., Tuominen, I., 1991, “Properties of mean field dynamos with non-axisymmetric α-effect”, Astron. Astrophys., 247, 576–579.
Moss, D., Barker, D.M., Brandenburg, A., Tuominen, I., 1995, “Nonaxisymmetric dynamo solutions and extended starspots on late-type stars”, Astron. Astrophys., 294, 155–164.
Mullan, D.J., 1975, “On the possibility of magnetic starspots on the primary components of W Ursae Majoris type binaries”, Astrophys. J., 198, 563–573.
Neff, J.E., O’Neal, D., Saar, S.H., 1995, “Absolute Measurements of Starspot Area and Temperature: II Pegasi in 1989 October”, Astrophys. J., 452, 879–893.
Noyes, R.W., Hartmann, L.W., Baliunas, S.L., Duncan, D.K., Vaughan, A.H., 1984, “Rotation, convection, and magnetic activity in lower main-sequence stars”, Astrophys. J., 279, 763–777.
Olah, K., Panov, K.P., Pettersen, B.R., Valtaoja, E., Valtaoja, L., 1988, “Long-lived active longitudes on the spotted RS CVn star a Germinorum”, Astron. Astrophys., 218, 192–194.
Olson, E.C., Etzel, P.B., 1993, “Cool-star photometric activity in six totally-eclipsing Algol binaries”, Astron. J., 106, 342–347.
O’Neal, D., Neff, J.E., 1997, “OH 1.563 µm absorption from starspots on active stars”, Astron. J., 113, 1129–1137.
O’Neal, D., Saar, S.H., Neff, J.E., 1996, “Measurements of Starspot Area and Temperature on Five Active, Evolved Stars”, Astrophys. J., 463, 766–775.
O’Neal, D., Neff, J.E., Saar, S.H., 1998, “Measurements of Starspot Parameters on Active Stars using Molecular Bands in Echelle Spectra”, Astrophys. J., 507, 919–937.
O’Neal, D., Neff, J.E., Saar, S.H., Mines, J.K., 2001, “Hydroxyl 1.563 Micron Absorption from Starspots on Active Stars”, Astron. J., 122, 1954–1964.
O’Neal, D., Neff, J.E., Saar, S.H., Cuntz, M., 2004, “Further Results of TiO-band Observations of Starspots”, Astron. J., 128, 1802–1811.
Pallavicini, R., 2002, “High-resolution ground-based spectroscopy: where and how?”, Astron. Nachr., 323, 288–293.
Pallavicini, R., Golub, L., Rosner, R., Vaiana, G.S., Ayres, T., Linsky, J.L., 1981, “Relations among stellar X-ray emission observed from Einstein, stellar rotation and bolometric luminosity”, Astrophys. J., 248, 279–290.
Petit, P., Donati, J.-F., Collier Cameron, A., 2002, “Differential rotation of cool active stars: the case of intermediate rotators”, Mon. Not. R. Astron. Soc., 334, 374–382.
Petit, P., Donati, J.-F., Collier Cameron, A., 2004, “Differential rotation of cool active stars”, Astron. Nachr., 325, 221–224.
Petrov, P.P., 2003, “T Tauri stars”, Astrophys., 46, 506–529.
Petrov, P.P., Shcherbakov, A.G., 1976, in Stars and galaxies from observational points of view, (Ed.) Kharadze, E.K., Proceedings of the Third European Astronomical Meeting, Tiflis, Georgian SSR, July 1–5, 1975, Third European Astron. Meeting, p. 163, Metsniereba, Tbilisi, USSR.
Petrov, P.P., Shcherbakov, V.A., Berdyugina, S.V., Shevchenko, V.S., Grankin, K.N., Melnikov, S.Y., 1994, “Photometric and spectroscopic observations of the spotted T Tauri star V410 Tauri”, Astrophys. J. Suppl. Ser., 107, 9–22.
Petrov, R.G., 1988, “Differential Speckle Imaging”, in High Resolution Imaging by Interferometry II: Ground-Based Interferometry at Visible and Infrared Wavelengths, (Ed.) Merkle, F., Proceedings of the NOAO-ESO Conference, held in Garching, Germany, 15–18 March 1988, vol. 29 of ESO Conference and Workshop Proc., p. 235, European Southern Observatory, Garching, Germany.
Piskunov, N.E., Kochukhov, O., 2002, “Doppler Imaging of stellar magnetic fields. I. Techniques”, Astron. Astrophys., 381, 736–756.
Piskunov, N.E., Wehlau, W.H., 1994, “The detectability of cool polar caps on late type stars”, Astron. Astrophys., 289, 868–870.
Piskunov, N.E., Tuominen, I., Vilhu, O., 1990, “Surface imaging of late-type stars”, Astron. Astrophys., 230, 363–370.
Radick, R.R., 2000, “A brief survey of chromospheric and photometric variability among sunlike stars”, Adv. Space Res., 26, 1739–1745.
Radick, R.R., Mihalas, D., Hartmann, L., Worden, S.P., Africano, J.L., Klimke, A., Tyson, E.T., 1982, “The photometric variability of solar-type stars. I. Preliminary results for the Pleiades, Hyades, and the Malmquist Field”, Publ. Astron. Soc. Pac., 94, 934–944.
Radick, R.R., Mihalas, D., Lockwood, G.W., Thompson, D.T., Warnock, A., Hartmann, L.W., Worden, S.P., Henry, G.W., Sherlin, J.M., 1983a, “The photometric variability of solar-type stars. III. Results from 1981–82, including parallel observations of thirty-six Hyades stars”, Publ. Astron. Soc. Pac., 95, 621–634.
Radick, R.R., Wilkerson, M.S., Worden, S.P., Africano, J.L., Klimke, A., Ruden, S., Rogers, W., Armandroff, T.E., Giampapa, M.S., 1983b, “The photometric variability of solar-type stars. II. Stars selected from Wilson’s chromospheric activity survey”, Publ. Astron. Soc. Pac., 95, 300–310.
Radick, R.R., Lockwood, G.W., Skiff, B.A., Baliunas, S.L., 1998, “Patterns of Variation among Sun-like Stars”, Astrophys. J. Suppl. Ser., 118, 239.
Reiners, A., Schmitt, J.H.M.M., 2002, “On the feasibility of the detection of differential rotation in stellar absorption profiles”, Astron. Astrophys., 384, 155–162.
Reiners, A., Schmitt, J.H.M.M., 2003a, “Rotation and differential rotation in field F- and G-type stars”, Astron. Astrophys., 398, 647–661.
Reiners, A., Schmitt, J.H.M.M., 2003b, “Differential rotation in rapidly rotating F-stars”, Astron. Astrophys., 412, 813–819.
Rice, J.B., 2002, “Doppler imaging of stellar surfaces — techniques and issues”, Astron. Nachr., 323, 220–235.
Rice, J.B., Strassmeier, K.G., 2000, “Doppler imaging from artificial data. Testing the temperature inversion from spectral-line profiles”, Astrophys. J. Suppl. Ser., 147, 151–168.
Rice, J.B., Wehlau, W.H., Khokhlova, V.L., 1989, “Mapping stellar surfaces by Doppler imaging — Technique and application”, Astron. Astrophys., 208, 179–188.
Richards, M.T., 1990, “The RS Canum Venaticorum characteristics of the infrared light curves of Algol”, Astrophys. J., 350, 372–385.
Robinson Jr, R.D., 1980, “Magnetic field measurements on stellar sources — A new method”, Astrophys. J., 239, 961–967.
Rodonò, M., Cutispoto, G., Pazzani, V., Catalano, S., Byrne, P.B., Doyle, J.G., Butler, C.J., Andrews, A.D., Blanco, C., Marilli, E., Linsky, J.L., Scaltriti, F., Busso, M., Cellino, A., Hopkins, J.L., Okazaki, A., Hayashi, S.S., Zeilik, M., Helston, R., Henson, G., Smith, P., Simon, T., 1986, “Rotational modulation and flares on RS CVn and BY Dra-type stars. I. Photometry and spot models for BY Dra, AU Mic, AR Lac, II Peg and V 711 Tau (= HR 1099)”, Astron. Astrophys., 165, 135–156.
Rodonò, M., Lanza, A.F., Catalano, S., 1995, “Starspot evolution, activity cycle and orbital period variation of the prototype active binary RS Canum Venaticorum”, Astron. Astrophys., 301, 75–88.
Rodonò, M., Messina, S., Lanza, A.F., Cutispoto, G., Teriaca, L., 2000, “The magnetic activity cycle of II Pegasi: results from twenty-five years of wide-band photometry”, Astron. Astrophys., 358, 624–638.
Rousselet-Perraut, K., Stehloe, C., Lanz, T., Le Bouquin, J.B., Boudoyen, T., Kilbinger, M., Kochukhov, O., Jankov, S., 2004, “Stellar activity and magnetism studied by optical inter-ferometry”, Astron. Astrophys., 422, 193–203.
Rüdiger, G., Hollerbach, R., 2004, The Magnetic Universe: Geophysical and Astrophysical Dynamo Theory, Wiley-VCH, Weinheim, Germany.
Rüdiger, G., Küker, M., 2002, “Meridional flow and differential rotation by gravity darkening in fast rotating solar-type stars”, Astron. Astrophys., 385, 308–312.
Rüdiger, G., von Rekowski, B., Donahue, R.A., Baliunas, S.L., 1998, “Differential rotation and meridional flow for fast-rotating solar-type stars”, Astrophys. J., 494, 691–699.
Rüedi, I., Solanki, S.K., Mathys, G., Saar, S.H., 1997, “Magnetic field measurements on moderately active cool dwarfs”, Astron. Astrophys., 318, 429–442.
Saar, S.H., 1988, “Improved methods for the measurement and analysis of stellar magnetic fields”, Astrophys. J., 324, 441–465.
Saar, S.H., 1994, “New Infrared Measurements of Magnetic Fields on Cool Stars”, in Infrared solar physics, (Eds.) Rabin, D.M., Jefferies, J.T., Lindsey, C., Proceedings of the 154th Symposium of the International Astronomical Union, held in Tucson, Arizona, U.S.A., March 2–6, 1992, p. 493, Kluwer Academic, Dordrecht, Netherlands; Boston, U.S.A.
Saar, S.H., Brandenburg, A., 1999, “Time Evolution of the Magnetic Activity Cycle Period: Results for an Expanded Stellar Sample”, Astrophys. J., 524, 295–310.
Saar, S.H., Linsky, J.L., 1985, “The photospheric magnetic field of the dM3.5e flare star AD Leonis”, Astrophys. J., 299, L47–L50.
Saar, S.H., Linsky, J.L., Beckers, J.M., 1986, “The magnetic field of the BY Draconis flare star EQ Virginis”, Astrophys. J., 302, 777–784.
Schüssler, M., 2002, “The formation of sunspots and starspots”, Astron. Nachr., 323, 377–382.
Schüssler, M., Solanki, S.K., 1992, “Why rapid rotators have polar spots”, Astron. Astrophys., 264, L13–L16.
Schüssler, M., Caligari, P., Ferriz-Mas, A., Solanki, S.K., Stix, M., 1996, “Distribution of starspots on cool stars. I. Young and main sequence stars of 1Msun”, Astron. Astrophys., 314, 503–512.
Selam, S.O., 2004, “Key parameters of W UMa-type contact binaries discovered by HIPPARCOS”, Astron. Astrophys., 416, 1097–1105.
Semel, M., 1989, “Zeeman-Doppler imaging of active stars. I — Basic principles”, Astron. Astrophys., 225, 456–466.
Semel, M., Li, J., 1996, “Zeeman-Doppler imaging of solar-type stars: Multi line technique”, Solar Phys., 164, 417–428.
Semel, M., López Ariste, A., 2001, “Current ground-based stellar spectropolarimeters and their use for Zeeman-Doppler imaging”, in Magnetic Fields Across the Hertzsprung-Russell Diagram, (Eds.) Mathys, G., Solanki, S.K., Wickramasinghe, D.T., Proceedings of a workshop held in Santiago, Chile, 15–19 January 2001], vol. 248 of ASP Conference Series, pp. 575–580, Astronomical Society of the Pacific, San Francisco, U.S.A.
Semel, M., Donati, J.-F., Rees, D.E., 1993, “Zeeman-Doppler imaging of active stars. 3. Instrumental and technical considerations”, Astron. Astrophys., 278, 231–237.
Simon, T., Fekel, F.C., 1987, “The dependence of ultraviolet chromospheric emission upon rotation among late-type stars”, Astrophys. J., 316, 434–448.
Skumanich, A., 1972, “Time Scales for CA II Emission Decay, Rotational Braking, and Lithium Depletion”, Astrophys. J., 171, 565–567.
Solanki, S.K., 2002, “The magnetic structure of sunspots and starspots”, Astron. Nachr., 323, 165–177.
Stelzer, B., Fernández, M., Costa, V.M., Gameiro, J.F., Grankin, K.N., Henden, A., Guenther, E.W., Mohanty, S., Flaccomio, E., Burwitz, V., Jayawardhana, R., Predehl, P., Durisen, R.H., 2003, “The weak-line T Tauri star V410 Tau. I. A multi-wavelength study of variability”, Astron. Astrophys., 411, 517–531.
Stenflo, J.O., 2001, “Limitations and opportunities for the diagnostics of solar and stellar magnetic fields”, in Magnetic Fields Across the Hertzsprung-Russell Diagram, (Eds.) Mathys, G., Solanki, S.K., Wickramasinghe, D.T., Proceedings of a workshop held in Santiago, Chile, 15–19 January 2001], vol. 248 of ASP Conference Series, pp. 639–650, Astronomical Society of the Pacific, San Francisco, U.S.A.
Stewart, R.T., Slee, O.B., White, G.L., Budding, E., Coates, D.W., Thompson, K., Bunton, J.D., 1989, “Radio emission from EA eclipsing binaries — Evidence for kilogauss surface fields on both early-type and late-type stars”, Astrophys. J., 342, 463–466.
Strassmeier, K.G., 1988, “A multiple spot model for simultaneous solution of light curves and distorted line profiles of spotted stars”, Astrophys. Space Sci., 140, 223–235.
Strassmeier, K.G., 1999, “Doppler imaging of stellar surface structure. XI. The super starspots on the K0 giant HD 12545: larger than the entire Sun”, Astron. Astrophys., 347, 225–234.
Strassmeier, K.G., 2002, “Doppler images of starspots”, Astron. Nachr., 323, 309–316.
Strassmeier, K.G., 2005, “Stellar activity cycles: observing the dynamo?”, Astron. Nachr., 326, 269–277.
Strassmeier, K.G., Bartus, J., 2000, “Doppler imaging of stellar surface structure. XII. Rapid spot changes on the RS CVn binary V711 Tauri = HR 1099”, Astron. Astrophys., 354, 537–550.
Strassmeier, K.G., Bopp, B.W., 1992, “Time-series photometric spot modeling. I — Parameter study and application to HD 17433 = VY Arietis”, Astron. Astrophys., 259, 183–197.
Strassmeier, K.G., Rice, J.B., 1998, “Doppler imaging of stellar surface structure. VI. HD 129333 = EK Draconis: a stellar analog of the active young Sun”, Astron. Astrophys., 330, 685–695.
Strassmeier, K.G., Rice, J.B., Wehlau, W.H., Vogt, S.S., Hatzes, A.P., Tuominen, I., Hackman, T., Poutanen, M., Piskunov, N.E., 1991, “Doppler imaging of high-latitude spot activity on HD 26337”, Astron. Astrophys., 247, 130–147.
Strassmeier, K.G., Bartus, J., Cutispoto, G., Rodonò, M., 1997, “Starspot photometry with robotic telescopes: Continuous UBV and V(RI)c photometry of 23 stars in 1991–1996”, Astrophys. J. Suppl. Ser., 125, 11–63.
Strassmeier, K.G., Lupinek, S., Dempsey, R.C., Rice, J.B., 1999, “Doppler imaging of stellar surface structure. X. The FK Comae-type star HD 199178 = V 1794 Cygni”, Astron. Astrophys., 347, 212–224.
Strassmeier, K.G., Pallavicini, R., Rice, J.B., Andersen, M.I., Zerbi, F.M., 2004, “The science case of the PEPSI high-resolution echelle spectrograph and polarimeter for the LBT”, Astron. Nachr., 325, 278–298.
Tas, G., Evren, S., 2000, “II Pegasi reached the largest amplitude up to now”, Inform. Bull. Var. Stars, 4992, 1.
Terebizh, V.Y., 1995, “Image restoration with minimum a priori information”, Phys. Usp., 38, 137–167.
Torres, C.A.O., Ferraz Mello, S., 1973, “On variable dMe stars”, Astron. Astrophys., 27, 231–236.
Torres, G., Ribas, I., 2002, “Absolute dimensions of the M-type eclipsing binary YY Geminorum (Castor C): A challenge to evolutionary models in the lower Main Sequence”, Astrophys. J., 567, 1140–1165.
Tuominen, I., Berdyugina, S.V., Korpi, M.J., 2002, “Starspot cycles from Doppler imaging and photometric time series as nonlinear dynamo”, Astron. Nachr., 323, 367–370.
Udalski, A., Szymański, M., Kałuzny, J., Kubiak, M., Mateo, M., Krzemiński, W., 1995, “The Optical Gravitational Lensing Experiment. The Catalog of Periodic Variable Stars in the Galactic Bulge. II. Periodic Variables in Four Baade’s Window Fields: BW1, BW2, BW3 and BW4”, Acta Astron., 45, 1–235.
Umana, G., Catalano, S., Rodonò, M., Gibson, D.M., 1989, “Radio Emission from Selected Algol Systems”, Space Sci. Rev., 50, 370.
Unruh, Y.C., Collier Cameron, A., 1995, “The sensitivity of Doppler imaging to line profile models”, Mon. Not. R. Astron. Soc., 273, 1–16.
Unruh, Y.C., Collier Cameron, A., 1997, “Does chromospheric emission mimic polar starspots in Doppler images?”, Mon. Not. R. Astron. Soc., 290, L37–L42.
Valenti, J.A., Johns-Krull, C.M., 2001, “Magnetic Field Measurements for Cool Stars”, in Magnetic Fields Across the Hertzsprung-Russell Diagram, (Eds.) Mathys, G., Solanki, S.K., Wickramasinghe, D.T., Proceedings of a workshop held in Santiago, Chile, 15–19 January 2001, vol. 248 of ASP Conference Series, pp. 179–188, Astronomical Society of the Pacific, San Francisco, U.S.A.
Valenti, J.A., Marcy, G.W., Basri, G., 1995, “Infrared Zeeman analysis of ϵ Eridani”, Astrophys. J., 439, 939–956.
van Leeuwen, F., Evans, D.W., Grenon, M., Grossmann, V., Mignard, F., Perryman, M.A.C., 1997, “The HIPPARCOS mission: photometric data”, Astron. Astrophys., 323, L61–L64.
Varricatt, W.P., 2000, “Photometric studies of close binary systems”, Bull. Astron. Soc. India, 28 321–327.
Vaughan, A.H., Preston, G.W., Baliunas, S.L., Hartmann, L.W., Noyes, R.W., Middelkoop, F., Mihalas, D., 1981, “Comparison of activity cycles in old and young main-sequence stars”, Astrophys. J., 250, 276–283.
Vilhu, O., 1984, “The nature of magnetic activity in lower main sequence stars”, Astron. Astrophys., 133, 117–126.
Vincent, A., Piskunov, N.E., Tuominen, I., 1993, “Surface imaging of eclipsing binary stars. 1: Techniques”, Astron. Astrophys., 278, 523–541.
Vogt, S.S., 1979, “A spectroscopic and photometric study of the star spot on HD 224085”, Publ. Astron. Soc. Pac., 91, 616.
Vogt, S.S., 1981, “A method for unambiguous determination of starspot temperatures and areas — Application to II Pegasi, BY Draconis, and HD 209813”, Astrophys. J., 250, 327–340.
Vogt, S.S., Penrod, G.D., 1983, “Doppler Imaging of spotted stars: Application to the RS Canum Venaticorum star HR 1099”, Publ. Astron. Soc. Pac., 95, 565–576.
Vogt, S.S., Penrod, G.D., Hatzes, A.P., 1987, “Doppler images of rotating stars using maximum entropy image reconstruction”, Astrophys. J., 321, 496–515.
Vogt, S.S., Hatzes, A.P., Misch, A.A., Kürster, M., 1999, “Doppler Imagery of the Spotted RS Canum Venaticorum Star HR 1099 (V711 Tauri) from 1981 to 1992”, Astrophys. J. Suppl. Ser., 121, 547–589.
Wade, G.A., 2003, “Measuring the characteristics of magnetic fields in A, B and O stars”, in Magnetic Fields in O, B and A Stars: Origin and Connection to Pulsation, Rotation and Mass Loss, (Eds.) Balona, L.A., Henrichs, H.F., Medupe, R., Proceedings of a conference held at University of North-West, Mmabatho, South Africa, 27 November — 1 December, 2002, vol. 305 of ASP Conference Series, p. 16, Astronomical Society of the Pacific, San Francisco, U.S.A.
Walter, F.M., Bowyer, S., 1981, “On the coronae of rapidly rotating stars. I. The relation between rotation and coronal activity in RS CVn systems”, Astrophys. J., 245, 671–676.
Webbink, R.F., 1976, “The evolution of low-mass close binary systems. I. The evolutionary fate of contact binaries”, Astrophys. J., 209, 829–845.
White, N.E., Marshall, F.E., 1983, “An X-ray survey on nine algol systems”, Astrophys. J., 268, L117–L120.
Wickramasinghe, D.T., Ferrario, L., 2000, “Magnetism in Isolated and Binary White Dwarfs”, Publ. Astron. Soc. Pac., 112, 873–924.
Willson, R.C., Gulkis, S., Janssen, M., Hudson, H.S., Chapman, G.A., 1981, “Observations of Solar Irradiance Variability”, Science, 211, 700–702.
Wilson, O.C., 1978, “Chromospheric variations in main-sequence stars”, Astrophys. J., 226, 379–396.
Wittkowski, M., Schoüller, M., Hubrig, S., Posselt, B., von der Lühe, O., 2002, “Measuring starspots on magnetically active stars with the VLTI”, Astron. Nachr., 323, 241–250.
Woodard, M.F., Noyes, R.W., 1985, “Change of Solar Oscillation Eigenfrequencies with the Solar Cycle”, Nature, 318, 449.
Wright, J.T., 2004, “Do we know of any Maunder minimum stars?”, Astron. J., 128, 1273–1278.
Zeilik, M., de Blasi, C., Rhodes, M., Budding, E., 1988, “A half-century of starspot activity on SV Camelopardalis”, Astrophys. J., 332, 293–298.
Acknowledgements
The support by Swiss National Foundation (grant 200021-103696/1) and Academy of Finland (grant 43039) is acknowledged.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Berdyugina, S.V. Starspots: A Key to the Stellar Dynamo. Living Rev. Sol. Phys. 2, 8 (2005). https://doi.org/10.12942/lrsp-2005-8
Published:
DOI: https://doi.org/10.12942/lrsp-2005-8