Population Pharmacodynamic Parameter Estimation from Sparse Sampling: Effect of Sigmoidicity on Parameter Estimates

Abstract

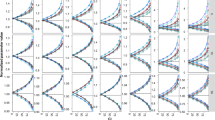
The objective of this stimulation study was to evaluate effect of simoidicity of the concentration–effect (C–E) relationship on the efficiency of population parameter estimation from sparse sampling and is a continuation of previous work that addressed the effect of sample size and number of samples on parameters estimation from sparse sampling for drugs with C–E relationship characterized by high sigmoidicity (γ > 5). The findings are based on observed C–E relationships for two drugs, octreotide and remifentanil, characterized by simple E _max and sigmoid E _max models (γ = ~2.5), respectively. For each model, C–E profiles (100 replicates of 100 subjects each) were simulated for several sampling designs, with four or five samples/individual randomly obtained from within sampling windows based on EC₅₀-normalized plasma drug concentrations, PD parameters based on observed population mean values, and inter-individual and residual variability of 30% and 25%, respectively. The C–E profiles were fitted using non-linear mixed effect modeling with the first-order conditional estimation method; variability parameters were described by an exponential error model. The results showed that, for the sigmoid E _max model, designs with four or five samples reliably estimated the PD parameters (EC₅₀, E _max, E ₀, and γ), whereas the five-sample design, with two samples in the 2–3 E _max region, provided in addition more reliable estimates of inter-individual variability; increasing the information content of the EC₅₀ region was not critical as long as this region was covered by a single sample in the 0.5–1.5 EC₅₀ window. For the simple E _max model, because of the shallower profile, enriching the EC₅₀ region was more important. The impact of enrichment of appropriate regions for the two models can be explained based on the shape (sigmoidicity) of the concentration–effect relationships, with shallower C–E profiles requiring data enrichment in the EC₅₀ region and steeper curves less so; in both cases, the E _max region needs to be adequately delineated, however. The results provide a general framework for population parameter estimation from sparse sampling in clinical trials when the underlying C–E profiles have different degrees of sigmoidicity.