1 Introduction

The rapid evolution of quantum information science is forging a quantum paradigm of processing information through superposition and entanglement in a parallel and secure manner, leading to quantum advantage [1,2,3,4]. In pursuit of a quantum internet that connects distant quantum processors, the ability to transmit quantum information encoded into long-lived superposition states becomes vital, and information carriers such as flying photon qubits in the superposition of two polarization states of photons have been utilized [5,6,7,8]. Despite these exciting developments, a mounting technological barrier still exists concerning high-channel capacity transmission links, with the quantum data rate limited to 110 Mb/s to date [9]. A promising solution is to prepare, manipulate, and transmit the fundamental unit of quantum information by high-dimensional superposition states (i.e., flying qudits) [10, 11]. For their intrinsic high dimensionality, qudits can encode richer information and provide more intricate entanglement structure, which are eligible for more efficient quantum algorithms and can thus further enlarge the information capacity and noise resilience for the development of the quantum internet [12,13,14,15,16].

To prepare flying qudits for high-capacity, noise-resilient quantum communication, long-distance quantum coherence is essential in the high-dimensional Hilbert space [17]. In particular, the eigenstates for constructing photon qudits via superpositions must be indistinguishable in terms of their fundamental characteristics, including spatial distribution and temporal overlap of different eigenstates. In parallel, richer superpositions that come with a higher dimensionality also require more sophisticated manipulations for flying qudits: arbitrary control of an N-dimensional qudit necessitates the precise manipulation of 2 (N-1) parameters simultaneously [18, 19]. Compared to the N-dimensional qudit built upon frequencies [20, 21] or time-bin [22,23,24], the exploitation of more than one degree of freedom (DOF) of light in the construction of the Hilbert space leads to simultaneous yet individual control over multiple DOFs, yielding more convenient and flexible manipulation of flying qudits [25,26,27,28]. Specifically, the polarization and spatial mode DOFs of light can synergistically synthesize a high-dimensional spin–orbit Hilbert space featuring robust quantum coherence, ideal for high-dimensional quantum communication. To date, generation and manipulation of spin–orbit structured photons have primarily relied on free-space bulk optics. Spiral phase plates and spatial light modulators have demonstrated their efficacy for producing complex spin–orbit structured photons [29]. Furthermore, geometric phase elements have been adopted in simpler configurations to yield four-dimensional (4D) spin–orbit mutually unbiased bases (MUBs) for quantum key distribution [27], and also hold promise for generating arbitrary spin–orbit SU (4) states [30]. Concurrently, integrated photonics have been broadly employed for state manipulation in path [31], frequency [20, 21] and time-bin [24] DOFs due to its scalability and robustness. While this technology has been widely applied for efficient generation of structured light [32], the potential for the creation and reconfiguration of entangled photonic spin–orbit states for quantum application have not been extensively explored. Here, we introduce a novel methodology to create, encode, and arbitrarily reconfigure spin–orbit structured photons and their formed flying qudits using an integrated photonic platform. The process starts with the generation of a biphoton polarization entangled state in free space, followed by the transfer of the signal photon into an integrated photonic circuit for the spin–orbit state manipulation, during which the quantum coherence and bi-photon entanglement are preserved within the entire process. Moreover, intrinsic entanglement associated with a bi-photon state further increases the dimensionality of the system, through the formation of three-qubit cluster states with greater channel capacity and higher noise resistance [33, 34] to accelerate quantum networking.

2 Results

Beyond the polarization states (also called photon spins: \(\left|\uparrow \right.\rangle\) and \(\left|\downarrow \right.\rangle\)) used in conventional qubits on a two-level Poincare sphere (PS), we construct qudits by the superposition of spin–orbit states [18, 35, 36] that carry coupled photon spin and orbital angular momentum (OAM). This forms a high-order PS (HOPS) with states \(\left|\uparrow , \pm l\right.\rangle\) and \(\left|\downarrow , \pm l\right.\rangle\) where l is the OAM order [18]. Through HOPS where multiple DOFs of light are at play, our qudits transcend the quantum system into higher dimensions. For a given OAM order l, it is worth emphasizing that the four spin–orbit eigenstates travel at the same speed and feature identical modal characteristics and far-field divergence, which guarantees indistinguishability in both space and time and yields long-distance coherence that is essential for building flying photon qudits [37]. While previous research has successfully generated these states using free space optical elements such as spatial light modulators and q-plates [27, 30, 38,39,40], the task of preparing and manipulating the spin–orbit entangled states within an integrated system in a scalable and robust way [41] still remains a significant challenge.

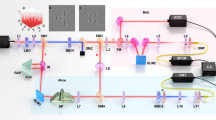
Here, we demonstrate an on-chip integrated experimental scheme with dual functionalities, i.e., preparing a single photon in an arbitrary spin–orbit SU (4) state as well as creating the high-dimensional bi-photon entanglement between the two photons in SU (4) and SU (2) spaces. To form such an entanglement structure, a bi-photon polarization-entangled state is first generated by the SPDC process [42]: \(|{\Psi }_{1}\rangle =\frac{1}{\sqrt{2}}(|{H}_{s}\rangle |{V}_{i}\rangle -|{V}_{s}\rangle |{H}_{i}\rangle )\), where H and V denote horizontal and vertical polarizations and s and i represent signal and idler photons, respectively. The idler photon remains in free space for the remote entanglement manipulation on the signal photon, whereas the signal photon is sent to the photonic integrated circuits (Fig. 1a) after passing through a polarization beam splitter which transforms the polarization DOF to the path DOF (see Supplementary Information). In this scenario, the superposition state of the signal photon in an SU (2) polarization space is translated to the superposition between on-chip waveguide modes \(\left|{1}_{s}\right.\rangle\) and \(\left|{3}_{s}\right.\rangle\). To expand the dimensionality for the signal photon, two Mach–Zehnder interferometers are strategically designed to perform two parallel on-chip SU (2) transformations with respect to inputs at \(\left|{1}_{s}\right.\rangle\) and \(\left|{3}_{s}\right.\rangle\), transforming the bi-photon entangled state \(|{\Psi }_{1}\rangle\) to

$$|{\Psi }_{2}\rangle =\frac{1}{\sqrt{2}}\left(\left({\text{cos}}\frac{{\theta }_{1}}{2}|{1}_{s}\rangle +{e}^{i{\varphi }_{1}}{\text{sin}}\frac{{\theta }_{1}}{2}|{2}_{s}\rangle \right)|{V}_{i}\rangle -\left({\text{cos}}\frac{{\theta }_{2}}{2}|{3}_{s}\rangle +{e}^{i{\varphi }_{2}}{\text{sin}}\frac{{\theta }_{2}}{2}|{4}_{s}\rangle \right)|{H}_{i}\rangle \right),$$
(1)

where \(\left|{2}_{s}\right.\rangle\) and \(\left|{4}_{s}\right.\rangle\) are other two waveguide modes paired with \(\left|{1}_{s}\right.\rangle\) and \(\left|{3}_{s}\right.\rangle\) (Fig. 1a), respectively, and \({\theta }_{1}\) (\({\theta }_{2}\)) and \({\varphi }_{1}\) (\({\varphi }_{2}\)) correspond to the relative amplitudes and phase between \(\left|{1}_{s}\right.\rangle\) and \(\left|{2}_{s}\right.\rangle\) (\(\left|{3}_{s}\right.\rangle\) and \(\left|{4}_{s}\right.\rangle\)), efficiently controlled by four on-chip phase shifters. Next, the four waveguide modes are translated to the four desired spin–orbit states, by coupling to two same-sized microring resonators (R1 and R2) with two different angular gratings. These gratings scatter the signal photon into the free-space Bessel modes with distinct spin–orbit locking [43] (see Supplementary Information), i.e., from \(\left|{1}_{s}\right.\rangle\) and \(\left|{2}_{s}\right.\rangle\) to \(\left|{\uparrow }_{s}, {+l}_{s}\right.\rangle\) and \(\left|{\downarrow }_{s}, {-l}_{s}\right.\rangle\) on HOPS I (via R1) and from \(\left|{3}_{s}\right.\rangle\) and \(\left|{4}_{s}\right.\rangle\) to \(\left|{\uparrow }_{s}, {-l}_{s}\right.\rangle\) and \(\left|{\downarrow }_{s}, {+l}_{s}\right.\rangle\) on HOPS II (via R2). In this process, \({\theta }_{1}\) (\({\theta }_{2}\)) and \({\varphi }_{1}\) (\({\varphi }_{2}\)) mentioned above control the latitude and longitude of the superposition state on HOPS I (II) (Fig. 1b), respectively. This procedure results in the entanglement of the signal photon’s spin–orbit state, characterized by the HOPS sets, with the idler photon’s polarization state, represented by the PS, as depicted in Fig. 1b. We would like to point out that although the local transformation applied to the signal photon preserves the original Schmidt number of 2 which quantifies the entanglement between the signal and idler photon [44], it increases the dimensionality of the signal photon to 4. In this scenario, the 4D spin–orbit space associated with the signal photon defines a single-photon qudit with a dimensionality of N = 4, formed by the four spin–orbit states of the signal photon. Along with its entanglement with the idler photon (i.e., Eq. (1)), it can lead to a multidimensional entangled state featuring a dimensionality of 2N [45].

Fig. 1
figure 1

Schematic for generation and manipulation of spin–orbit flying qudits. The signal photon from a pair of polarization-entangled photons, after passing through a polarized beam splitter, are injected into the integrated circuits (upper panel of a) through waveguide modes \(|{1}_{s}\rangle\) and\(|{3}_{s}\rangle\). Two on-chip Mach–Zehnder (MZ) interferometers transforms the signal photon into a SU(4) space, spanned by 4 waveguide modes and visualized by the orange high-order Poincare sphere (HOPS) sets in b. Four phase shifters H1, H3, H2, and H4 can control the latitude (\({\theta }_{1}\),\({\theta }_{2}\)) and the longitude (\({\varphi }_{1}\),\({\varphi }_{2}\)) on HOPS I and II. Subsequently, the waveguide modes are coherently transformed to four spin–orbit states\(|{\uparrow }_{s},+{6}_{s}\rangle\),\(|{\uparrow }_{s},-{6}_{s}\rangle\), \(|{\downarrow }_{s},-{6}_{s}\rangle\) and \(|{\downarrow }_{s},+{6}_{s}\rangle\) through two ring resonators R1 and R2 with scatterers inscribed at their inner sidewalls (see Supplementary Information). Meanwhile, the idler photon spans a two-dimensional Hilbert space depicted by the blue Poincare sphere (PS) in b, which is entangled with the signal photon’s HOPS set. This entanglement facilitates the convenient access of HOPS III, which completes the arbitrary generation and reconfiguration of the signal photon’s spin–orbit SU (4) state. The lower panel of a shows the scanning electron microscope (SEM) image of the photonic integrated circuits. Also note that two orange arrows shown in a represent two different modes of signal photons, rather than two distinct photons

Full size image

The full state reconfiguration of the signal photon in the designed spin–orbit SU (4) space is completed by leveraging the signal-idler photon entanglement, where the polarization manipulation and post selection of the idler photon on its PS can provide two independent parameters to remotely project the superposition state of the signal photon on HOPS III. This manipulation enables the coupling between HOPS I and II via HOPS III to form the complete high-dimensional SU(4) hyper-HOPS for the signal photon:

$$|{\psi }_{s}\rangle =\frac{1}{\sqrt{2}}\left(\alpha \left({\text{cos}}\frac{{\theta }_{1}}{2}|{\uparrow }_{s},+{l}_{s}\rangle +{e}^{i{\varphi }_{1}}{\text{sin}}\frac{{\theta }_{1}}{2}|{\downarrow }_{s},-{l}_{s}\rangle \right)+\beta \left({\text{cos}}\frac{{\theta }_{2}}{2}|{\uparrow }_{s},-{l}_{s}\rangle +{e}^{i{\varphi }_{2}}{\text{sin}}\frac{{\theta }_{2}}{2}|{\downarrow }_{s},+{l}_{s}\rangle \right)\right),$$
(2)

where α and β are complex coefficients from the polarization manipulation and post selection of the idler photon (i.e., \(\left|{\psi }_{i}\right.\rangle ={\beta }^{*}\left|{H}_{i}\right.\rangle -{\alpha }^{*}\left|{V}_{i}\right.\rangle\)), satisfying the relation of \({\left|\alpha \right|}^{2}+{\left|\beta \right|}^{2}=1\). The post selection process facilitates a superposition pure state for the signal photon, constituted by 4 spin–orbit eigenstates \(|{\uparrow }_{s},+{l}_{s}\rangle , |{\downarrow }_{s},-{l}_{s}\rangle , |{\uparrow }_{s},-{l}_{s}\rangle\) and \(|{\downarrow }_{s},+{l}_{s}\rangle\), defining a flying qudit which can be conveniently configured in an arbitrary spin–orbit SU (4) state. Note that the 4D qudit we constructed here consists of the spin and OAM degrees of freedom of a single photon, which is fundamentally different from the system composed of two entangled qubits carried by two separate photons [46].

The photonic integrated circuit including Mach–Zehnder interferometers coupled with microring resonators was fabricated on a Si3N4-on-SiO2 platform. The cross-section of the waveguides and microrings was designed to be 550 nm × 300 nm to support the desired spin–orbit locking for the SPDC-generated entangled photons at the wavelength of approximately 810 nm. The angular gratings inscribed on microring resonators R1 and R2 were also carefully designed with the scatterers' size of 80 nm × 80 nm × 300 nm, such that their emissions carry opposite OAM orders under the same photon spin (\(l=\pm 6\)), matching the designed spin–orbit eigenstates on HOPS I and II (Fig. 1b). In each Mach–Zehnder interferometer, two cascaded thermal-based phase shifters together perform the SU(2) transformation on the signal photon by tuning \({\theta }_{\mathrm{1,2}}\) and \({\varphi }_{\mathrm{1,2}}\), transforming to the bi-photon state denoted in Eq. (1). In the experiment, the spin–orbit states on HOPS I and II were tuned to \(|{\psi }_{s1}\rangle =\frac{1}{\sqrt{2}}(\left|{\uparrow }_{s}, {+6}_{s}\right.\rangle +\left|{\downarrow }_{s}, {-6}_{s}\right.\rangle )\) and \(|{\psi }_{s2}\rangle =\frac{1}{\sqrt{2}}(\left|{\uparrow }_{s}, {-6}_{s}\right.\rangle +\left|{\downarrow }_{s}, {+6}_{s}\right.\rangle )\), which served as the north and south pole states of HOPS III, respectively (Fig. 2a). To demonstrate the high-dimensional coherent manipulation needed for a photon qudit, we further manipulated the polarization state of the idler photon to remotely maneuver the signal photon switching between four iconic states: the aforementioned two pole states \(|{\psi }_{s1}\rangle\) and \(|{\psi }_{s2}\rangle\) on HOPS III, and two 4D states \(|{\psi }_{s3}\rangle =\frac{1}{\sqrt{2}}(|{\psi }_{s1}\rangle +|{\psi }_{s2}\rangle )\) and \(|{\psi }_{s4}\rangle =\frac{1}{\sqrt{2}}(|{\psi }_{s1}\rangle -i|{\psi }_{s2}\rangle )\) on the equator as superpositions of the two pole states. Quantum state tomography was subsequently conducted to fully characterize the complete 4D quantum state of the signal photon through sixteen separate projection measurements in each tomography process (see Supplementary Information), when the polarization state of the idler photon was tuned from the two poles of its PS (\(|{\psi }_{i1}\rangle =|{V}_{i}\rangle\) and \(|{\psi }_{i2}\rangle =|{H}_{i}\rangle\)) to the equator at \(|{\psi }_{i3}\rangle =\frac{1}{\sqrt{2}}(|{H}_{i}\rangle -|{V}_{i}\rangle )\) and \(|{\psi }_{i4}\rangle =\frac{1}{\sqrt{2}}(|{H}_{i}\rangle +i|{V}_{i}\rangle )\), corresponding to \(|{\psi }_{s1}\rangle\) to \(|{\psi }_{s4}\rangle\) for the signal photon, respectively (Fig. 2b). The experimentally reconstructed density matrix of the signal photon in the 4D spin–orbit Hilbert space exhibits great consistency with the theory, confirmed by high quantum fidelities for all four spin–orbit states with an average quantum fidelity of 92.6% (see Supplementary Information). Here, the imperfection of the quantum fidelities is mainly attributed to the instability of the relative phase between different off-chip paths and the light coupling from free space to the on-chip waveguide, and can be alleviated by utilizing active feedback control or making the generation scheme fully integrated through employing an on-chip spontaneous four-wave mixing (SFWM) entanglement source [47]. Moreover, the impurities of the transverse spin at the inner sidewall of the ring resonator could also cause the degradation of the quantum state, which could be further optimized towards unity by fine-tuning the resonator's width and height [48].

Fig. 2
figure 2

Integrated generation and manipulation of the high-dimensional spin–orbit SU(4) state. a The locations of four selected iconic spin–orbit states on the HOPS set of the signal photon, where the states are: \(|{\psi }_{s1}\rangle =\frac{1}{\sqrt{2}}(|{\uparrow }_{s},+{6}_{s}\rangle +|{\downarrow }_{s},-{6}_{s}\rangle )\), \(|{\psi }_{s2}\rangle =\frac{1}{\sqrt{2}}(|{\uparrow }_{s},-{6}_{s}\rangle +|{\downarrow }_{s},+{6}_{s}\rangle )\), \(|{\psi }_{s3}\rangle =\frac{1}{\sqrt{2}}(|{\psi }_{s1}\rangle +|{\psi }_{s2}\rangle )\) and \(|{\psi }_{s4}\rangle =\frac{1}{\sqrt{2}}(|{\psi }_{s1}\rangle -i|{\psi }_{s2}\rangle )\). b The experimentally retrieved (upper row) and theoretically predicted (lower row) density matrices \({\rho }_{s}=|{\psi }_{s}\rangle \langle {\psi }_{s}|\) of the four quantum states depicted in a. The spin–orbit states are generated by appropriately biasing the on-chip optical phase shifters and projecting the idler photon into \(|{\psi }_{i1}\rangle =|{V}_{i}\rangle\), \(|{\psi }_{i2}\rangle =|{H}_{i}\rangle\), \(|{\psi }_{i3}\rangle =\frac{1}{\sqrt{2}}(|{H}_{i}\rangle -|{V}_{i}\rangle )\) and \(|{\psi }_{i4}\rangle =\frac{1}{\sqrt{2}}(|{H}_{i}\rangle +i|{V}_{i}\rangle )\), respectively. The experimental density matrices are reconstructed through full quantum tomography with 16 projective measurements. The quantum fidelities are 93.3%, 96.2%, 91.0% and 90.0%, respectively, with an average high fidelity of 92.6%, validating the capability of the coherent generation and reconfiguration of the high-dimensional spin–orbit SU (4) states

Full size image

The ability to prepare the flying photon qudit is the key to high-dimensional quantum key distribution for robust and noise-resilient quantum communication. According to the high-dimensional BB84 protocol [10,11,12, 49], two mutually unbiased bases \(\left\{|{\alpha }_{i}\rangle \right\}\) and \(\left\{|{\beta }_{j}\rangle \right\}\) with 4 states each can be created using eight orthogonal superpositions of any paired spin–orbit eigenstates satisfying \({\left|\langle {\alpha }_{i}|{\alpha }_{j}\rangle \right|}^{2}={\left|\langle {\beta }_{i}|{\beta }_{j}\rangle \right|}^{2}={\delta }_{ij}\) and \({\left|\langle {\alpha }_{i}|{\beta }_{j}\rangle \right|}^{2}=\frac{1}{4}\). Here, the mutually unbiased bases are chosen to be: \(\left\{\left|{\alpha }_{i}\rangle \right.\right\}=\frac{1}{\sqrt{2}}\left\{|{\uparrow }_{s},+{6}_{s}\rangle +|{\uparrow }_{s},-{6}_{s}\rangle , |{\uparrow }_{s},+{6}_{s}\rangle -|{\uparrow }_{s},-{6}_{s}\rangle , |{\downarrow }_{s},+{6}_{s}\rangle +|{\downarrow }_{s},-{6}_{s}\rangle , |{\downarrow }_{s},+{6}_{s}\rangle -|{\downarrow }_{s},-{6}_{s}\rangle \right\}\) and \(\left\{\left|{\beta }_{i}\rangle \right.\right\}=\frac{1}{\sqrt{2}}\left\{|{\uparrow }_{s},+{6}_{s}\rangle +|{\downarrow }_{s},+{6}_{s}\rangle , |{\uparrow }_{s},+{6}_{s}\rangle -|{\downarrow }_{s},+{6}_{s}\rangle , |{\uparrow }_{s},-{6}_{s}\rangle +|{\downarrow }_{s},-{6}_{s}\rangle , |{\uparrow }_{s},-{6}_{s}\rangle -|{\downarrow }_{s},-{6}_{s}\rangle \right\}\). In practice, the two mutually unbiased bases shared between the transmitter (Alice) and the receiver (Bob) together form an 8 × 8 probability-of-detection matrix (Fig. 3a), where each matrix element represents the probability of the quantum state prepared by the transmitter to be decoded by the receiver. The experimentally reconstructed matrix (Fig. 3b), after 64 projective measurements, demonstrated a high preparation fidelity of 86.9% (well above the protocol threshold of 81.1%), confirming the viability of applying the generated flying photon qudit for quantum communication. In this scenario, we simulated the image encryption transmission from the transmitter to the receiver under the high-dimensional BB84 protocol (Fig. 3c) [50], where the photonic state was randomly prepared at \(|{\alpha }_{i}\rangle\) or \(|{\beta }_{i}\rangle\) by the transmitter and retrieved by the receiver based on the measured probability-of-detection matrix (see Supplementary Information). To transmit this colored image, the RGB values in each pixel were discretized into four levels and subsequently encrypted by quantum keys corresponding to \(|{\alpha }_{i}\rangle\) or \(|{\beta }_{i}\rangle\). The reconstructed image successfully reproduced the original image, which demonstrated the capability of secure communication using spin–orbit qudits. Compared with the conventional protocol using flying qubits, the 4D qudits enabled the transmission of doubled bits of information while maintaining the same single photon generation rate. Additionally, the quantum bit error rate threshold also increases from 11.0% to 18.9%, granting efficient quantum data transfer with enhanced noise resilience. It is worth to mention that reaching a high secret key rate with such 4D qudits requires the deterministic detection of spin–orbit states. This could be potentially achieved through the efficient OAM sorting technique that has demonstrated an experimental separation efficiency of over 92% [51]. With this foundation, we anticipate assessing the practicality of our generation scheme by conducting real-time quantum key distribution experiments under true environmental conditions in our subsequent research.

Fig. 3
figure 3

Demonstration of the potential towards high-dimensional quantum key distribution. a and b are the theoretically and experimentally retrieved probability-of-detection matrix, respectively, in which each row and column label the state prepared by the transmitter and decoded by the receiver, respectively. The experimentally reconstructed matrix shows a preparation fidelity of 86.85% exceeding the protocol threshold of 81.1%, validating the feasibility of conducting high-dimensional quantum key distribution. c Simulated secret communication using the high-dimensional BB84 protocol for quantum key distribution. With the experimentally measured probability-of-detection matrix, the transmitter and receiver can share a series of secret keys using the protocol. The original image’s RGB values of each pixel are discretized into four levels (left panel) and then encrypted using the transmitter’s quantum keys sequentially (middle panel). The encrypted image is subsequently sent to the receiver and decoded with the receiver’s secret keys after information reconciliation (right panel)

Full size image

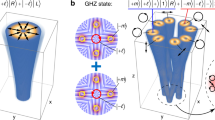
The entanglement between the signal and idler photon is maintained throughout the integrated manipulation process, allowing for the exploitation of the whole biphoton system, which further expands the dimensionality of the Hilbert space. In our experimental scheme, the Hilbert space of the biphoton state is a tensor product space of three two-dimensional systems: the spin and the OAM degrees of freedom for the signal photon, alongside the spin degree of freedom for the idler photon. Together, they constitute an eight-dimensional (8D) Hilbert space, characterizing a three-qubit quantum system. (Fig. 4a). One significant group of quantum states in this Hilbert space is the high-dimensional cluster state with versatile graph structures [52], featuring a greater channel capacity. In comparison to the multi-qubit system with a single DOF, our high-dimensional spin–orbit system conveniently offers simultaneous control of two DOFs as well as the two-qubit operation over different DOFs of the same particle, which greatly facilitates the generation and manipulation of complex cluster states in a flexible way [25, 33, 53]. By performing the local unitary operation on the idler photon where two pole states of the PS are transformed to two superposition states (i.e., \(|{A}_{i}\rangle =\frac{1}{\sqrt{2}}(|{H}_{i}\rangle -|{V}_{i}\rangle )\) and \(|{D}_{i}\rangle =\frac{1}{\sqrt{2}}(|{H}_{i}\rangle +|{V}_{i}\rangle )\)), we can successfully generate a linearly connected three-qubit cluster state:

$$|\Psi _{{cluster}} \rangle = \frac{1}{{\sqrt 8 }}\left( {| \uparrow _{s} , + 6_{s} \rangle + | \downarrow _{s} , + 6_{s} \rangle + | \uparrow _{s} , - 6_{s} \rangle + | \downarrow _{s} , - 6_{s} \rangle } \right)|A_{i} \rangle + \frac{1}{{\sqrt 8 }}\left( {| \uparrow _{s} , + 6_{s} \rangle - | \downarrow _{s} , + 6_{s} \rangle - | \uparrow _{s} , - 6_{s} \rangle + | \downarrow _{s} , - 6_{s} \rangle } \right)|D_{i} \rangle$$

in which the spin and OAM DOFs of the signal photon are correlated with the spin DOF of the idler photon, as illustrated in the graph representation in Fig. 4a. The genuine multipartite entanglement structure brings exotic coupled polarization and intensity distribution of the optical field (Fig. 4b), enabling the controllability of the spatial field distribution of the signal photon via the manipulation and the polarization projection of the idler photon. The generated cluster state was characterized with a full quantum tomography consisting of 64 projective measurements (see Supplementary Information). The retrieved density matrix \({\rho }_{cluster}=|{\Psi }_{cluster}\rangle \langle {\Psi }_{cluster}|\) demonstrated a quantum fidelity of 88.4%, verifying the system in a high-dimensional entangled quantum state. The successful generation of the high-fidelity cluster state, due to the greater channel capacity, allows the encoding of complex quantum information capable of quantum error correction [33], thereby further enhancing the robustness of the quantum channel. Moreover, the integrated generation scheme of cluster states, which can be further scaled up, holds the promise of mitigating quantum losses to establish long-range quantum communication without the need for excessive quantum memories [34]. Additionally, the created cluster states may enable the essential infrastructure for the practical deployment of one-way quantum computation [52, 53]. Note that the fidelity of the spin–orbit hybrid entangled states generated in our system is lower compared to high-dimensional entanglements within a single degree of freedom reported in other literatures. This is primarily due to the instabilities of our experimental setup instead of the fundamental limitation of the generation scheme, which could be mitigated by adopting a fully integrated generation approach with on-chip SFWM source [47].

Fig. 4
figure 4

Eight-dimensional cluster state in the spin–orbit entanglement space spanned by signal and idler photons. a The PS representation and the graph representation of the three-qubit cluster state. The coupled HOPSs structure illustrates the eight-dimensional Hilbert space spanned by the spin (\({S}_{s}\)) and OAM (\({O}_{s}\)) of the signal photon and the spin (\({S}_{i}\)) of the idler photon. The center blue PS represents the idler photon space spanned by \(|{A}_{i}\rangle\) and \(|{D}_{i}\rangle\) obtained after performing the local unitary transformation with respect to the idler photon PS in Fig. 1a, while the top (bottom) panel shows the four-dimensional spin–orbit Hilbert space of the signal photon with projecting the idler photon onto the pole state \(|{A}_{i}\rangle\) (\(|{D}_{i}\rangle\)). The solid points on each sphere depict the projection of the cluster state onto the corresponding HOPS. The black dashed panel illustrates the graph representation of the constructed cluster state \(|{\Psi }_{cluster}\rangle\). The spin of the signal photon \({S}_{s}\), the spin of the idler photon \({S}_{i}\), and the OAM of the signal photon \({O}_{s}\) are sequentially and linearly connected, showing that the state is a simultaneous + 1-eigenvalue eigenstate of \({\sigma }_{x,{S}_{s}}\otimes {\sigma }_{z,{S}_{i}}\otimes {I}_{{O}_{s}}\), \({\sigma }_{z,{S}_{s}}\otimes {\sigma }_{x,{S}_{i}}\otimes {\sigma }_{z,{O}_{s}}\) and \({I}_{{S}_{s}}\otimes {\sigma }_{z,{S}_{i}}\otimes {\sigma }_{x,{O}_{s}}\), where \(I\), \({\sigma }_{x}\), \({\sigma }_{z}\) are identity matrix and Pauli matrices for the corresponding DOFs. b The spatial field distribution of the generated cluster state, where the top and bottom panels show the polarization and intensity distribution of the cluster state. The orange images, light green arrows, and blue arrows denote the intensity and polarization distribution of the signal photon and the polarization of the idler photon, respectively. c Experimentally reconstructed (top panel) and theoretically predicted (bottom panel) density matrix \({\rho }_{cluster}=|{\Psi }_{cluster}\rangle \langle {\Psi }_{cluster}|\), featuring a high quantum fidelity of 88.4%

Full size image

3 Discussion

In summary, we demonstrated the convenient generation and flexible manipulation of high-dimensional quantum states in a spin–orbit coupled Hilbert space. Integrating the generated spin–orbit structured photons into the pre-existing fiber network infrastructure [54, 55] offers promising prospects for a fiber-based high-dimensional quantum key distribution system that could potentially achieve elevated secret key rates [56]. With the same propagation constant and spatial profile, these quantum states maintain long-distance coherence, delivering a flying photon qudit for high-capacity, long-haul quantum network. This characteristic makes them excellent candidates for establishing satellite-based intercontinental secure quantum communication, which exhibits smaller loss and higher secure key rate compared to the fiber-based quantum communication over equivalent distances [7]. Note that integrated photonics has been applied to the generation of structured light, complementary to the conventional approaches based on free space optics [32]. While our work is focused on 4D qudits, the demonstrated on-chip platform is highly scalable to support even a higher-dimensional Hilbert space, making it of broad significance for constructing high-dimensional quantum networks. Further integration of on-chip SFWM quantum sources can lead to a fully integrated generation scheme [47], enhancing resistance to the inefficiencies of free-space to on-chip waveguide coupling and fluctuations in free-space setups, thereby establishing a robust entanglement distribution source suited for quantum satellites and ground stations with a higher quantum data rate and fidelity.