WCNS schemes and some recent developments

Abstract

Weighted compact nonlinear schemes (WCNS) are a family of nonlinear shock capturing schemes that are suitable for solving problems with discontinuous solutions. The schemes are based on grids staggered by flux points and solution points, resulting in algorithms with the nonlinear interpolation step independent of the difference step. Thus, only linear difference operators are needed, such that geometric conservation law can be preserved easily, resulting in the preservation of freestream condition. In recent years, these schemes have attracted a lot of attention in the community of computational fluid dynamics. This paper intends to give a brief review of the basic algorithms of these schemes and present some related recent developments.

1 Introduction

With the fast growth of computational capability, high-order methods play a more and more important role in the field of computational fluid dynamics. High-order schemes, usually referred to schemes with convergence rates higher than second-order, admit better resolution properties than their lower order counterparts. More importantly, high-order schemes may produce more accurate results than low-order schemes in terms of using the same computational cost. In the past three decades, great progress has been achieved for high-order schemes. Some representative schemes are widely used, such as weighted essentially non-oscillatory (WENO) schemes [1,2,3], weighted compact nonlinear schemes (WCNS) [4], discontinuous Galerkin schemes [5,6,7], spectral difference schemes [8,9,10], flux reconstruction schemes [11, 12], and so on.

WCNS schemes are a family of high-order schemes that are suitable for solving problems with discontinuous solutions. These schemes are originally developed for addressing shock-capturing problems of compact linear schemes [13]. Although dissipation can be introduced to improve the shock capturing capability of compact linear schemes [14], oscillations are difficult to be removed for strong shocks. Therefore, nonlinear schemes are often needed. In [15, 16], based on grids staggered by flux points and solution points, compact nonlinear schemes were developed by employing the idea of ENO schemes for the interpolation step. Later on, the idea of WENO schemes was introduced further to construct WCNS schemes [4, 17]. Since then, WCNS schemes were further developed and widely used in applications [18]. Some benchmark examples were presented in [19] to demonstrate the efficiency of WCNS schemes. They were used in Reynolds-averaged Navier-Stokes (RANS) simulations [20,21,22,23,24,25,26], large eddy simulations (LES) [27,28,29,30,31,32], hybrid RANS/LES simulations [33, 34], and even direct numerical simulations (DNS) [35]. Some important phenomena were also investigated by applying these schemes. The areas include boundary layer transition [36,37,38,39,40], acoustic wave [41,42,43,44], vortices [45], interaction between shock wave and vortex [46, 47], detonation [48,49,50], body-wake interactions [51], Mach reflection [52], elastic-plastic deformation [53], multi-component compressible flows [54], magnetohydrodynamics [55], and so on.

Compared with WENO schemes, WCNS schemes have some advantages, mainly lying in the flexibility of the choice of numerical fluxes and the convenience of preserving geometric conservation law. In this paper, we provide a brief review of WCNS schemes, aiming at introducing some basic ideas of the algorithms and presenting some recent developments. The rest of this paper is arranged as follows. In Section 2, the basic algorithm of WCNS schemes is given. In Section 3, conservative boundary closures are discussed. In Section 4, geometric conservation law that arises from coordinate transform is presented. To preserve this law numerically, a symmetric conservative metric method (SCMM) is also introduced. Finally, concluding remarks are given in Section 5.

2 Algorithm of WCNS schemes

To describe WCNS schemes, let us consider the one-dimensional conservation law

$$\begin{aligned} u_t + f(u)_x = 0, \end{aligned}$$

(1)

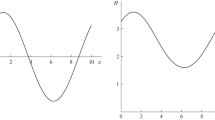
where $u=u(x,t)$ denotes the conservative quantity and f(u) is the flux. As illustrated in Fig. 1, the spatial interval [a, b] is divided into N subintervals by flux points

$$\begin{aligned} x_{j+1/2} = a + j h, \quad 0\le j \le N, \end{aligned}$$

(2)

where $h = (b-a)/N$ stands for the length of the interval. The solution points, denoted by $x_j$, are placed at the center of the subintervals $[x_{j-1/2},x_{j+1/2}]$, i.e.,

$$\begin{aligned} x_j = ( x_{j-1/2}+x_{j+1/2} )/2, \quad 1\le j \le N. \end{aligned}$$

(3)

Fig. 1

Illustration of the grid staggered by flux points and solution points

2.1 Basic procedure

At time t, suppose the values of u at solution points $x_j$ are known, denoted by $u_j$. Then the spatial discretization algorithm of WCNS schemes can be summarized as the following three steps:

• (i) Apply interpolation schemes to obtain the left and right values at flux points $x_{j+1/2}$, denoted by $u_{j+1/2}^L$ and $u_{j+1/2}^R$, respectively.

• (ii) Compute the numerical flux $f_{j+1/2}=\hat{f}\left(u_{j+1/2}^L,u_{j+1/2}^R\right)$, where $\hat{f}$ denotes some approximate Riemann solvers.

• (iii) Employ difference schemes to calculate the flux derivatives at solution points $x_{j}$, denoted by $f^\prime _{j}$.

After spatial discretization, we obtain a system of ordinary differential equations

$$\begin{aligned} \frac{du_j}{dt} + f^\prime _j = 0, \end{aligned}$$

(4)

which can be solved by some time-marching schemes, such as the explicit Runge-Kutta scheme [56], the two-stage fourth-order scheme [57], and some other implicit schemes [58, 59]. It shall be mentioned that one can also perform interpolation for the flux directly as done in [60]. However, in that case the nonlinearity is performed for the flux, leading to the difficulty in preserving geometric conservation law, which is very important for applications to complex configurations.

2.2 Interpolation schemes

For the interpolation step, many interpolation schemes can be applied. For smooth solutions, linear interpolation schemes can be applied, such as explicit upwind interpolation schemes [61], compact upwind linear interpolation schemes [13], dissipative compact linear interpolation schemes [62, 63], and so on.

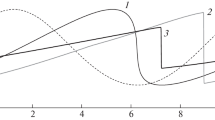
Here, we introduce a fifth-order interpolation scheme [4] for the left values, while the right values can be obtained according to the symmetry property of the grids. As illustrated in Fig. 2, to get the left values $u_{j+1/2}^L$ at flux points $x_{j+1/2}$, the following explicit upwind fifth-order interpolation scheme can be derived, i.e.,

$$\begin{aligned} u_{j+1/2}^L = \frac{3}{128}u_{j-2}-\frac{5}{32}u_{j-1}+\frac{45}{64}u_j+\frac{15}{32}u_{j+1}-\frac{5}{128}u_{j+2}, \end{aligned}$$

(5)

where the coefficients can be obtained by using the method of Lagrangian interpolation. However, this scheme is not suitable for the case with discontinuous solutions. To address this problem, one may first decompose the fifth-order scheme (5) as

$$\begin{aligned} u_{j+1/2}^L = \sum _{k=0}^2 \gamma _k u_{j+1/2}^{(k)}, \end{aligned}$$

(6)

where $u_{j+1/2}^{(k)}$ are third-order interpolation schemes with different stencils, expressed as

$$\begin{aligned} u^{(0)}_{j+1/2}&= \frac{3}{8}u_{j-2}-\frac{5}{4}u_{j-1}+\frac{15}{8}u_j,\end{aligned}$$

(7)

$$\begin{aligned} u^{(1)}_{j+1/2}&= -\frac{1}{8}u_{j-1}+\frac{3}{4}u_j+\frac{3}{8}u_{j+1},\end{aligned}$$

(8)

$$\begin{aligned} u^{(2)}_{j+1/2}&= \frac{3}{8}u_j+\frac{3}{4}u_{j+1}-\frac{1}{8}u_{j+2}, \end{aligned}$$

(9)

and $\gamma _k$ are linear optimal weights with values

$$\begin{aligned} \gamma _0=\frac{1}{16},\quad \gamma _1 = \frac{5}{8},\quad \gamma _2 = \frac{5}{16}. \end{aligned}$$

(10)

Fig. 2

Illustration of the stencil used for the fifth-order interpolation scheme (5)

Then, following the recipe of WENO schemes [3] we introduce nonlinear weights defined by

$$\begin{aligned} \omega _k = \frac{\alpha _k}{\alpha _0+\alpha _1+\alpha _2}, \end{aligned}$$

(11)

where

$$\begin{aligned} \alpha _k = \frac{\gamma _k}{(\beta _k+\varepsilon )^2}. \end{aligned}$$

(12)

Here, the small parameter $\varepsilon$ is set to be $10^{-6}$ to avoid the denominator becoming zero, and $\beta _k$ are smoothness indicators of the interpolation schemes applied to compute $u_{j+1/2}^{(k)}$, defined by

$$\begin{aligned} \beta _0&= ( u_{j-2} - 2 u_{j-1} + u_j )^2+\frac{1}{4}(u_{j-2} - 4 u_{j-1} + 3 u_{j})^2, \end{aligned}$$

(13)

$$\begin{aligned} \beta _1&= ( u_{j-1} - 2 u_{j} + u_{j+1} )^2+\frac{1}{4}(u_{j-1} - u_{j+1})^2 ,\end{aligned}$$

(14)

$$\begin{aligned} \beta _2&= ( u_{j} - 2 u_{j+1} + u_{j+2} )^2+\frac{1}{4}(3 u_{j} - 4 u_{j+1} + u_{j+2} )^2. \end{aligned}$$

(15)

Finally, we obtain the fifth-order shock capturing interpolation scheme

$$\begin{aligned} u_{j+1/2}^L = \sum _{k=0}^2 \omega _k u^{(k)}_{j+1/2}. \end{aligned}$$

(16)

However, it was pointed out in [64] that the scheme (16) based on the nonlinear weights defined by Eqs. (11) and (12) may degenerate to third-order at critical points. To address this issue, one can implement the idea of improving the performance of WENO schemes for the nonlinear interpolation step of WCNS schemes. In particular, we present here a recent work [65] such that the optimal fifth-order convergence rate can be achieved for any smooth solutions, i.e., regardless of the order of critical points. The scheme can still be written in the form of Eq. (16), where $\omega _k$ are still given by Eq. (11), but with $\alpha _k$ defined by

$$\begin{aligned} \alpha _k = \gamma _k \exp ( -\beta _k^\lambda /\lambda ). \end{aligned}$$

(17)

Here, $\beta _k$ are still given by Eqs. (13)-(15), and $\lambda$ is a parameter defined by

$$\begin{aligned} \lambda = \max \left( e^{-3\theta }, 10^{-6} \right),\quad \theta = \frac{\tau }{ (\beta _{\min }+\varepsilon )^{0.8}}, \end{aligned}$$

(18)

where

$$\begin{aligned} \tau = |\beta _2-\beta _0|,\quad \beta _{\min } = \min _{k=0,1,2} \beta _k,\quad \varepsilon = 10^{-40}. \end{aligned}$$

(19)

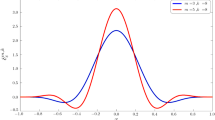
It can be seen from Fig. 3 that $\alpha _k$ are more sensitive to the values of $\beta _k$ for smaller value of $\lambda$. For smooth solutions, the definition of $\lambda$ (18) satisfies the condition

$$\begin{aligned} \lim _{h\rightarrow 0} \lambda = 1. \end{aligned}$$

(20)

Fig. 3

The exponential function involved in Eq. (17)

Since the smoothness indicators defined by Eqs. (13)-(15) obey the relations $\beta _k = \mathcal {O}(h^2)$, we have

$$\begin{aligned} \alpha _k = \gamma _k + \mathcal {O}(h^2). \end{aligned}$$

(21)

This condition ensures that the corresponding scheme (16) is fifth-order, regardless of the order of critical points.

There are some other methods for improving the performance of the nonlinear interpolation schemes. For example, low-dissipation WCNS schemes were constructed in [66,67,68,69,70,71]. In [72,73,74], compact nonlinear interpolation schemes were developed to improve the resolution of WCNS schemes. The ideas of targeted ENO schemes and multi-resolution WENO schemes were introduced for the interpolation step of WCNS schemes in [75] and [76, 77], respectively. A parameter-free $\varepsilon$-adaptive algorithm was also proposed in [78, 79] to improve the performance of WCNS schemes.

2.3 Difference schemes

By using interpolation schemes, we can get the left and right values at flux points $x_{j+1/2}$. Then various approximate Riemann solvers [80,81,82] can be applied to compute the numerical fluxes $f_{j+1/2}$ at flux points $x_{j+1/2}$. It shall be mentioned that both flux vector splitting and flux difference splitting methods are applicable here for WCNS schemes, while only flux vector splitting methods can be applied for reconstruction-based WENO schemes. In [83,84,85,86], the effect of flux evaluation methods for WCNS schemes was investigated in details. Here we pay attention to difference schemes.

It was shown in [87, 88] that the resolution of WCNS schemes is dominated by the compactness of the interpolation step, while it is less related to the difference step. Therefore, the difference scheme is usually chosen to be an explicit one for the purpose of efficiency. For instance, the sixth-order explicit central difference scheme presented in [87, 89] reads as

$$\begin{aligned} f^\prime _j = \frac{75}{64} \frac{f_{j+1/2}-f_{j-1/2}}{h} -\frac{25}{128}\frac{f_{j+3/2}-f_{j-3/2}}{3 h} +\frac{3}{128}\frac{f_{j+5/2}-f_{j-5/2}}{5 h}. \end{aligned}$$

(22)

For the reason of robustness, some other hybrid difference schemes involving both the fluxes at flux points and solution points can also be used. For example, the sixth-order scheme presented in [90] can be written as

$$\begin{aligned} f'_j&=\alpha \frac{ f_{j+1/2}-f_{j-1/2} }{h} + \frac{192-175\alpha }{256}\frac{ f_{j+1}-f_{j-1} }{h} + \frac{35\alpha -48}{320}\frac{ f_{j+2}-f_{j-2} }{h} \nonumber \\&\quad + \frac{64-45\alpha }{3840}\frac{ f_{j+3}-f_{j-3} }{h}, \end{aligned}$$

(23)

where $\alpha \ge 0$ is a parameter that can be tuned to control its dissipation property. The sixth-order difference scheme implemented in [91] is expressed as

$$\begin{aligned} f'_j=\frac{3}{2}\frac{ f_{j+1/2}-f_{j-1/2} }{h} - \frac{3}{10}\frac{ f_{j+1}-f_{j-1} }{h} + \frac{1}{30}\frac{ f_{j+3/2}-f_{j-3/2} }{h}. \end{aligned}$$

(24)

It was shown that WCNS schemes can benefit from linear difference operators in terms of preserving geometric conservation law [92, 93]. It shall also be mentioned that alternative WENO schemes were proposed in [94], where the WENO reconstruction is employed for the variable rather than the flux. Thus, linear difference operators can be applied directly. It shall be mentioned that the alternative WENO schemes are closely related to WCNS schemes, as pointed out in [95, 96]. Since it is not easy to find the original conference paper [95] for the derivation in details, we present the demonstration of the relation in Appendix A.

3 Conservative boundary closures

Compared to interior schemes of WCNS schemes, boundary closures are seldom considered theoretically. Although some concerns have been mentioned in previous works, the stability issue has not been clearly investigated. By using the result of Gustafsson [97], the order of boundary closures should be at most one order lower than that of the interior for first-order hyperbolic conservation laws. Otherwise, the global convergence rate cannot be equal to the order of the interior. For Cartesian grids, the inverse Lax-Wendroff method [98,99,100] may be applied to derive the boundary closures. However, this method is difficult for applications to practical problems. In most cases, we may need curvilinear grids and apply biased schemes near boundary.

For WCNS schemes, conservative boundary closures were derived based on global conservation in [61]. Some applications can also be found in [101, 102]. The derivation is based on the difference scheme consisting of only flux points, like the sixth-order difference scheme (5). For a more general case, we introduce here the method used in [61] and consider the 2rth-order difference scheme

$$\begin{aligned} f^\prime _j = \sum _{k=1}^r \alpha _k \frac{ f_{j+k-1/2}-f_{j-k+1/2} }{(2k-1)h},\quad r \le j \le N-r+1, \end{aligned}$$

(25)

where the coefficients $\alpha _k$ can be determined according to the order condition. For instance, one can apply the method of Lagrangian interpolation to get the values of $\alpha _k$ as tabulated in Table 1 for $2\le r \le 6$.

Table 1 The values of $\alpha _k$ in Eq. (25) for $2\le r\le 6$

To mimic the global conservation property of the one-dimensional conservation law (1), i.e.,

$$\begin{aligned} \frac{d}{dt}\int _a^b u dx = f(u(a,t))-f(u(b,t)), \end{aligned}$$

(26)

we first rewrite the interior difference scheme (25) into a conservative form

$$\begin{aligned} f^\prime _j = \frac{\widetilde{f}_{j+1/2} - \widetilde{f}_{j-1/2}}{h}, \end{aligned}$$

(27)

where

$$\begin{aligned} \widetilde{f}_{j+1/2} = \sum \limits _{k=1}^r \frac{\alpha _k}{2k-1} \sum \limits _{l=j-k+1}^{j+k-1} f_{l+1/2}. \end{aligned}$$

(28)

Then we define the interior operator as

$$\begin{aligned} \mathcal {I}[f] = \sum \limits _{j=r}^{N-r+1} f_j^\prime = \frac{ \widetilde{f}_{N-r+3/2}-\widetilde{f}_{r-1/2} }{ h}. \end{aligned}$$

(29)

Finally, we introduce the left and right boundary operators, written respectively as

$$\begin{aligned} \mathcal {L}[f] = \frac{ \widetilde{f}_{r-1/2} - f_{1/2} }{h} \end{aligned}$$

(30)

and

$$\begin{aligned} \mathcal {R}[f] = \frac{ f_{N+1/2} - \widetilde{f}_{N-r+3/2} }{h}, \end{aligned}$$

(31)

such that the following global conservation property holds

$$\begin{aligned} (\mathcal {L}[f] +\mathcal {I}[f] +\mathcal {R}[f] )h = f_{N+1/2}-f_{1/2}. \end{aligned}$$

(32)

Now what we need to do is just to decompose the boundary operators as the sum of the difference schemes at solution points near boundary. Due to the symmetry property of the grid, we only have to consider the case for the left. It was shown in [61] that

$$\begin{aligned} \mathcal {L}[f] = \sum _{j=1}^{r-1} f^\prime (x_j) + \mathcal {O}(h), \end{aligned}$$

(33)

which means that there must be as least a near boundary difference scheme with only first order of accuracy if we require $\mathcal {L}[f] = \sum _{j=1}^{r-1} f^\prime _j$. To address this issue, we modified Eq. (33) to be

$$\begin{aligned} \mathcal {L}[f] = \sum _{j=1}^{r-1} \omega _j f^\prime (x_j^*) + \mathcal {O}(h^{2r-2}) , \end{aligned}$$

(34)

where the $2r-2$ unknowns, $\omega _j$ and $x_j^*$, are determined by the conditions of the accuracy. Here, the new introduced solution points $x_j^*$ are nonuniformly distributed, which are called conservative solution points. The detailed values of $\omega _j$ and $x_j^*$ can be found in [61]; see Eqs. (32)-(36) therein. That is to say, we replace the solution points near boundary with the conservative points and consider so-called semi-uniform grids, where the flux points are still uniformly distributed, as illustrated in Fig. 4.

Fig. 4

Illustration of the semi-uniform grid for the fifth-order WCNS scheme, where the two solution points near each boundary are replaced with the conservative solution points

To determine the conservative difference schemes near boundary, we first require that

$$\begin{aligned} \mathcal {L}[f] = \sum _{j=1}^{r-1} \omega _j f^\prime _j. \end{aligned}$$

(35)

Then we set the schemes $f^\prime _j$ to be $(2r-2)$th-order, determined by the following stencils

$$\begin{aligned} f^\prime _j = \frac{1}{h}\sum _{k=1}^{2r-1} a_{j,k} f_{k-1/2}, \end{aligned}$$

(36)

where the coefficients $a_{j,k}$ can be determined conveniently by using the method of Lagrangian interpolation. For the right-hand side, the boundary closures for the difference scheme can be obtained symmetrically.

For the interpolation step, we just need to apply interpolation schemes with biased stencils. Then we can construct boundary closures that are time stable up to eleventh order of global accuracy. For problems with discontinuous solutions near boundary, nonlinear shock-capturing boundary interpolation schemes were proposed recently in [103]. It was shown that the shock-capturing issue near boundary can be resolved well by using the idea of multi-resolution interpolation and the technique of tuning parameter in the smoothness indicators.

4 Geometric conservation law and SCMM method

For practical applications, it often necessitates to apply curvilinear grids. In that case, we shall consider conservation law in curvilinear coordinates. Since the pioneering work [104], some problems related to geometric conservation law have been studied by many researchers [92, 93, 105,106,107,108,109]. According to [110], the geometric conservation law can be classified as surface conservation law and volume conservation law. For static curvilinear grids, which is the case considered in this paper, the volume conservation law is satisfied automatically. Thus, we only need to consider the surface conservation law.

4.1 Surface conservation law

To describe the definition of the surface conservation law, let us consider the three-dimensional conservation law, written as

$$\begin{aligned} U_t + F_x + G_y + H_z = 0, \end{aligned}$$

(37)

where U denotes the conservative quantity, and F, G and H are fluxes in x, y and z directions, respectively. In curvilinear coordinates ($\xi ,\eta ,\zeta$) [111], Eq. (37) can be expressed as

$$\begin{aligned} (JU)_t + \left(\mathcal {F}\cdot \textbf{S}^{(\xi )}\right)_\xi + \left(\mathcal {F}\cdot \textbf{S}^{(\eta )}\right)_\eta + \left(\mathcal {F}\cdot \textbf{S}^{(\zeta )}\right)_\zeta = 0, \end{aligned}$$

(38)

where $\mathcal {F}=(F,G,H)$ is the tensor of the fluxes, and the Jacobian term J is defined as

$$\begin{aligned} J = \textbf{r}_\xi \cdot (\textbf{r}_\eta \times \textbf{r}_\zeta ), \end{aligned}$$

(39)

and the surface vectors $\textbf{S}^{(\xi )}$, $\textbf{S}^{(\eta )}$ and $\textbf{S}^{(\zeta )}$ are determined by

$$\begin{aligned} \textbf{S}^{(\xi )} = \textbf{r}_{\eta }\times \textbf{r}_{\zeta },\quad \textbf{S}^{(\eta )} = \textbf{r}_{\zeta }\times \textbf{r}_{\xi },\quad \textbf{S}^{(\zeta )} = \textbf{r}_{\xi }\times \textbf{r}_{\eta } \end{aligned}$$

(40)

with $\textbf{r}=(x,y,z)^T$. It is straightforward to check that the following relation holds, i.e.,

$$\begin{aligned} \left(\textbf{S}^{(\xi )}\right)_\xi + \left(\textbf{S}^{(\eta )}\right)_\eta + \left(\textbf{S}^{(\zeta )}\right)_\zeta = 0, \end{aligned}$$

(41)

which is the so-called surface conservation law.

4.2 SCMM method

In the context of discretization space, the surface conservation law (41) may not hold exactly, leading to geometric induced errors in the solution. It was shown that preserving the surface conservation law discretely is very important for high-order finite different schemes [106].

For low-order algorithms [104, 112], some techniques can be made to satisfy the surface conservation law discretely. For high-order finite different schemes, according to the knowledge of the authors, the most satisfied way so far is to apply the SCMM method with linear difference operators. This method is a further development of the conservative metric method (CMM) proposed in [92]. The CMM method can maintain the freestream property of the original conservation law and also improve the behavior of WCNS schemes for applications to curvilinear coordinates [18]. However, the CMM method does not admit appropriate geometric meaning that is similar with finite volume methods. To address this issue, the SCMM method was proposed in [93].

The SCMM method is based on the symmetric conservative form of the Jacobian (39) and the surface vectors (40), where the Jacobian is written as

$$\begin{aligned} J = \frac{1}{3} \left[\left(\textbf{r}\cdot \textbf{S}^{(\xi )} \right)_\xi + \left(\textbf{r}\cdot \textbf{S}^{(\eta )} \right)_\eta + \left(\textbf{r}\cdot \textbf{S}^{(\zeta )} \right)_{\zeta }\right], \end{aligned}$$

(42)

and the surface vectors are expressed as

$$\begin{aligned} \textbf{S}^{(\xi )} =&\frac{1}{2}\left[(\textbf{r}\times \textbf{r}_\zeta )_{\eta }+( \textbf{r}_\eta \times \textbf{r} )_\zeta \right],\end{aligned}$$

(43)

$$\begin{aligned} \textbf{S}^{(\eta )} =&\frac{1}{2}[(\textbf{r}\times \textbf{r}_\xi )_{\zeta }+( \textbf{r}_\zeta \times \textbf{r} )_\xi ],\end{aligned}$$

(44)

$$\begin{aligned} \textbf{S}^{(\zeta )} =&\frac{1}{2}[(\textbf{r}\times \textbf{r}_\eta )_{\xi }+( \textbf{r}_\xi \times \textbf{r} )_\eta ]. \end{aligned}$$

(45)

For the SCMM method, linear difference operators are applied to discretize the metric derivatives. The discretization of the Jacobian term is denoted as

$$\begin{aligned} J_{j,k,l}&= \frac{1}{3} \delta ^1_\xi \left\{ \textbf{r}\cdot \frac{1}{2}\left[ \delta _\eta ^2 \left(\textbf{r}\times \delta _\zeta ^3 \textbf{r}\right)+ \delta _\zeta ^2 \left(\delta ^3_\eta \textbf{r}\times \textbf{r}\right) \right] \right\} _{j,k,l}\nonumber \\&\quad +\frac{1}{3} \delta ^1_\eta \left\{ \textbf{r}\cdot \frac{1}{2}\left[ \delta _\zeta ^2 \left(\textbf{r}\times \delta _\xi ^3 \textbf{r}\right) + \delta _\xi ^2 \left(\delta _\zeta ^3 \textbf{r}\times \textbf{r}\right) \right] \right\} _{j,k,l}\nonumber \\&\quad +\frac{1}{3} \delta ^1_\zeta \left\{ \textbf{r}\cdot \frac{1}{2}\left[ \delta _\xi ^2 \Big(\textbf{r}\times \delta _\eta ^3 \textbf{r}\Big) + \delta _\eta ^2 \left(\delta ^3_\xi \textbf{r}\times \textbf{r}\right) \right] \right\} _{j,k,l}, \end{aligned}$$

(46)

where $\delta _\xi ^n$, $\delta _\eta ^n$ and $\delta _\zeta ^n$ ($n=1,2,3$) denote the linear difference operators for $\xi$, $\eta$ and $\zeta$ directions, respectively. Here the superscripts are counted from outside to inside of the brackets.

The spatial term of Eq. (38) has a similar form to the Jacobian (42), and its discretized form can be expressed as

$$\begin{aligned} SDT_{j,k,l}&= \frac{1}{3} \delta ^1_\xi \left\{ \mathcal {F}\cdot \frac{1}{2}\left[ \delta _\eta ^2 \Big(\textbf{r}\times \delta _\zeta ^3 \textbf{r}\Big) + \delta _\zeta ^2 \Big(\delta ^3_\eta \textbf{r}\times \textbf{r}\Big) \right] \right\} _{j,k,l}\nonumber \\&\quad +\frac{1}{3} \delta ^1_\eta \left\{ \mathcal {F}\cdot \frac{1}{2}\left[ \delta _\zeta ^2 \Big(\textbf{r}\times \delta _\xi ^3 \textbf{r}\Big) + \delta _\xi ^2 \Big(\delta _\zeta ^3 \textbf{r}\times \textbf{r}\Big) \right] \right\} _{j,k,l}\nonumber \\&\quad +\frac{1}{3} \delta ^1_\zeta \left\{ \mathcal {F}\cdot \frac{1}{2}\left[ \delta _\xi ^2 \Big(\textbf{r}\times \delta _\eta ^3 \textbf{r}\Big) + \delta _\eta ^2 \Big(\delta ^3_\xi \textbf{r}\times \textbf{r}\Big) \right] \right\} _{j,k,l}. \end{aligned}$$

(47)

For freestream flow, U is constant, so is $\mathcal {F}$. In that case, if the linear difference operators satisfy the condition

$$\begin{aligned} \delta _\xi ^1=\delta _\xi ^2,\quad \delta _\eta ^1=\delta _\eta ^2,\quad \delta _\zeta ^1=\delta _\zeta ^2, \end{aligned}$$

(48)

then it is easy to observe from Eq. (47) that

$$\begin{aligned} SDT_{j,k,l} = 0. \end{aligned}$$

(49)

Therefore, the semi-discretized form of Eq. (38) becomes

$$\begin{aligned} \frac{d}{dt}(JU)_{j,k,l} = 0. \end{aligned}$$

(50)

Since static grids are considered here, the Jacobian is independent of time. Thus, we know from Eq. (50) that $U_{j,k,l}$ is constant, indicating that the freestream condition is preserved exactly. Actually, the condition (48) also ensures that the surface conservation law (41) is maintained discretely. However, if we intend to have some geometric meanings of the Jacobian, it is better to further require that

$$\begin{aligned} \delta _\xi ^1=\delta _\xi ^2=\delta _\xi ^3,\quad \delta _\eta ^1=\delta _\eta ^2=\delta _\eta ^3,\quad \delta _\zeta ^1=\delta _\zeta ^2=\delta _\zeta ^3, \end{aligned}$$

(51)

which is the condition of the SCMM method. In this case, the discretized value $J_{j,k,l}$ (46) represents a weighted sum of some volumes consisting of grid points in the physical space [113, 114].

5 Conclusions

In this paper, we have summarized some main algorithms of WCNS schemes and presented some related recent developments. The schemes are based on grids staggered by flux points and solution points. Thus, the spatial discretization is divided into the interpolation step and the difference step. This setup has benefit in the flexibility of choosing numerical fluxes. In addition, the nonlinear procedure is applied only to the interpolation step but not the difference step. Thus, the geometric conservation law can be preserved exactly in a discrete setting, providing that the introduced SCMM method is applied. We have also introduced the so-called conservative boundary closures for the difference step, such that the scheme is globally conservative and also time stable, with the global convergent rates as the same as the interior.

In future, some aspects of WCNS schemes are worth studying further, mainly lying in the improvement of their robustness, accuracy and resolution. To improve the robustness of the schemes for practical applications, one should address the issue of positivity preserving [115,116,117]. So far, how to preserve the positivity property and the geometric conservation law on curvilinear grids at the same time is still an open problem. Although a fifth-order WCNS scheme with unconditionally optimal convergence rate is available [65], the extension to other orders of accuracy shall be addressed. In addition, for a given grid the actual truncation error of a scheme is determined by its resolution. Thus, to improve the resolution property of WCNS schemes [118] deserves a further study as well.

Appendix A: Relation between WCNS and alternative WENO schemes

The alternative WENO schemes [94] for the one-dimensional conservation law (1) can be written as

$$\begin{aligned} \frac{d u_j}{dt} + \frac{\hat{f}_{j+1/2}-\hat{f}_{j-1/2}}{h} = 0, \end{aligned}$$

(52)

where

$$\begin{aligned} \hat{f}_{j+1/2}=f_{j+1/2}-\frac{1}{24} h^2 f_{xx}|_{j+1/2}+ \frac{7}{5760}h^4 f_{xxxx}|_{j+1/2} + \mathcal {O}(h^6). \end{aligned}$$

(53)

If we drop the truncation error and evaluate the derivatives in the above equation by the following central difference schemes,

$$\begin{aligned} f_{xx}|_{j+1/2} = \frac{1}{h^2} \left[ -\frac{17}{24} (f_j+f_{j+1})+\frac{13}{16}(f_{j-1}+f_{j+2}) - \frac{5}{48} (f_{j-2}+f_{j+3})\right] ,\end{aligned}$$

(54)

$$\begin{aligned} f_{xxxx}|_{j+1/2} = \frac{1}{h^4}\left[ (f_j+f_{j+1})-\frac{3}{2}(f_{j-1}+f_{j+2}) + \frac{1}{2} (f_{j-2}+f_{j+3})\right] , \end{aligned}$$

(55)

then we have

$$\begin{aligned} \hat{f}_{j+1/2} = f_{j+1/2}+\frac{59}{1920}(f_j+f_{j+1})-\frac{137}{3840}(f_{j-1}+f_{j+2})+\frac{19}{3840}(f_{j-2}+f_{j+3}). \end{aligned}$$

(56)

In this case, the spatial discretization term $(\hat{f}_{j+1/2}-\hat{f}_{j-1/2})/h$ in Eq. (52) is equal to that of the WCNS scheme (4) with the difference scheme

$$\begin{aligned} f_j^\prime = \frac{ f_{j+1/2}-f_{j-1/2} }{h} + \frac{17}{256}\frac{ f_{j+1}-f_{j-1} }{h} - \frac{13}{320}\frac{ f_{j+2}-f_{j-2} }{h} + \frac{19}{3840}\frac{ f_{j+3}-f_{j-3} }{h}, \end{aligned}$$

(57)

which is exactly the hybrid sixth-order difference scheme (23) with $\alpha =1$.