Introduction

With the interconnections of power system increasing, the instability assessment is becoming more and more important for safe operation of power systems. The power system stability refers to the continuance of intact operation following a disturbance, it depends on the operation and the nature of the physical disturbance [1, 2]. The 2003 blackout occurred in N.E. North America is partly because of the lack of supportive applications when the system is close to instability [3]. If power system is close to the stability limit, actions must be taken by system operators to identify critical states. Therefore, it is very important to have an index for the critical situation awareness. A series of disturbances can increasingly stress the system, degradation of its stability margin may finally lead to loss of stability. Therefore, the analysis of system dynamic response during or after the disturbance is very important to indicate the potential instability of the power system [4].

The conventional methods of power system analysis are based on numerical solution of system differential algebraic equations. These numerical methods need more detailed representation of the power system but they are not suited for online application of stability assessment and control. There are three reasons: 1) The power system dynamic model could not include all the details of the power system; 2) The topology of the power system changes all the time; 3) The long computation time of the numerical solution. With a large number of synchrophasors being deployed, it is possible to construct power system model based purely on real-time synchrophasor measurements, which also can make on-line power system instability awareness feasible. Studies have been done with the measurement data for the system instability assessment [5–11]. Some focus on using real-time phasor measurements with pre-existing knowledge obtained from computer simulation results or historical events to enable real-time assessment under disturbance conditions [8, 9]. Some use selected real-time measurement locations to directly compute energy functions for the potential of instability [10, 11]. An adaptive power system equivalent method for real-time estimation of stability margin using phase-plane trajectories was proposed in [7]. This paper proposes a new method for instability early warning only using continuous high-sampling-rate measurements. In order to create the system collapse case, the idea in [7] using a series of disturbances to stress the system was used in this paper. Then an index was proposed to assess the potential instability of the system.

The rest of the paper is organized as follows. Section II is the introduction of the measurement-based system dynamic response estimation model and the model accuracy index. Section III is to implement the proposed model accuracy index to evaluate the system instability. Section IV is the case study of the proposed method. Conclusion and future work are provided in Section V.

Methodology of the proposed approach

Dynamic response estimation

A concept of dynamic response estimation for power system was proposed in [12]. It is to estimate the dynamic response of the power system during or after disturbances. The basic idea of the dynamic response estimation is to identify the real-time dynamic model or the transfer function of the power system and use the obtained model to estimate the dynamic response of the power system.

The ARX model structure

Two categories of measurement-based models can be used for system identification: state-space model [13–17], and transfer function model [18–21]. The state-space representation is concerned not only with input and output properties of the system but also with its complete internal behavior [22]. In contrast, the transfer function representation is concerned with and specifies only the input/output behavior. Hence, the transfer function model identification can be an alternative to overcome the drawback of high computation burden of state-space methods. The linear Auto Regressive Exogenous model (ARX) provides a much simpler identification model of multi-variable system than the state-space model or other models. The general expression of the transfer function model structure [23] is:

$$ A(z)y(t)=\frac{B(z)}{F(z)}u(t)+\frac{C(z)}{D(z)}e(t) $$
(1)

where

\( \begin{array}{l}A(z)=1+{a}_1{z}^{-1}+\dots +{a}_{n_a}{z}^{-{n}_a},B(z)={b}_1{z}^{-1}+\dots +{b}_{n_b}{z}^{-{n}_b}\\ {}C(z)=1+{c}_1{z}^{-1}+\dots +{c}_{n_c}{z}^{-{n}_c},D(z)=1+{d}_1{z}^{-1}+\dots +{d}_{n_d}{z}^{-{n}_d}\\ {}F(z)=1+{f}_1{z}^{-1}+\dots +{f}_{n_f}{z}^{-{n}_f}\end{array} \) where t is the time index, and e(t) is a white noise, z −1 is a backward shift operator and z −1 y(t) = y(t-1). n a , n b , n c , n d , n f are the orders of the signal y(t), u(t), and e(t), respectively. If C(q) = 1,D(q) = 1 and F(q) = 1, then (1) becomes to be the AutoRegressive model with eXogenous inputs (ARX) model. The mathematical structure expression of the ARX model is also can be described by the equation:

$$ \begin{array}{l}y(t)+{a}_1y\left(t-1\right)+\cdots +{a}_{n_a}y\left(t-{n}_a\right)\\ {}={b}_0u(t)+{b}_1u\left(t-1\right)+\cdots +{b}_{n_b}u\left(t-{n}_b\right)+e(t)\end{array} $$
(2)

With the SISO ARX model structure (1), the multi-input single-output (MISO) ARX model structure can be derived:

$$ \begin{array}{l}y(t)+{a}_1y\left(t-1\right)+\cdots +{a}_{n_a}y\left(t-{n}_a\right)\\ {}={\displaystyle {\sum}_{j=1}^M\left({b}_{j0}{u}_j(t)+{b}_{j1}{u}_j\left(t-1\right)+\cdots +{b}_{j{n}_{bj}}{u}_j\left(t-{n}_{bj}\right)\right)}+e(t)\end{array} $$
(3)

For the simplification, (3) can be further expressed in the vector form as:

$$ \mathbf{a}\mathbf{y}(t)={\displaystyle {\sum}_{j=1}^M{\mathbf{b}}_j{\mathbf{u}}_j(t)}+\mathrm{e}(t) $$
(4)

where \( \mathbf{a}=\left[1,\kern0.5em {a}_1,\cdots, {a}_{n_a}\right],\mathbf{y}(t)=\left[\mathrm{y}(t),\mathrm{y}\left(t-1\right),\cdots, \mathrm{y}\left(t-{n}_a\right)\right] \) \( {\mathbf{b}}_j=\left[{b}_{j0},{b}_{j1},\cdots, {b}_{j{n}_{aj}}\right],{\mathbf{u}}_j(t)=\left[{u}_j(t),\cdots, {u}_j\left(t-{n}_{bj}\right)\right] \)

Because of the linear structure of the ARX model, the model parameters of a multi-input ARX model can be estimated by a linear Least Square (LS) approach. The objective function is

$$ M\mathrm{in}\kern0.5em J\left({V}_{LS}\right)={\displaystyle {\sum}_{\mathrm{k}={n}_{\mathrm{s}}+1}^N\left(\widehat{y}(k)-y\Big(k\right)}\Big){}^2 $$
(5)

where N is the total data points, ŷ(k)andy(k)are the actual response and estimated response, respectively.

Model accuracy index

To evaluate the identified ARX model, a fitness criterion can be performed [24]:

$$ F=\left(1-\frac{\sqrt{{\left(\widehat{Y}-Y\right)}^2}}{\sqrt{{\left(\widehat{Y}-\overline{Y}\right)}^2}}\right)\times 100 $$
(6)

where Y,Ŷ,\( \overline{Y} \) are the estimated response by the ARX model, measured response by PMU/FDR, and the mean value of the measured response, respectively. This index is the accuracy of the model estimation in describing system dynamic characteristics. A fitness of 100 means a perfect fit between the estimated response and the actual response, while a fitness of zero means the estimated response Y is no better than the mean value of measured response\( \overline{Y} \).

For easier interpretation, a normalization process that converts the accuracy index from (−∞, 100] to (0, 1] can be performed as followed:

$$ A={e}^{\left(F/100\right)-1} $$
(7)

where F is the fitness index defined in previous study and A is the normalized accuracy index. The accuracy index of instability assessment threshold can be determined as:

$$ T={A}_{\max } $$
(8)

whereA maxis the maximum one among all the calculated accuracy index in marginally stable cases. T is the maximum value of the accuracy index of the last disturbance before instability. The accuracy represents the difference between the actual response at the output location and the response estimated by the ARX model.

Method for instability awareness

Capability of accuracy index for instability warning

The application of the linear ARX-structured modeling method is under the assumption that the power system to be modeled is relatively linear around certain operation points. Although the power system is nonlinearin nature, the operating point of the large-scale power grid does not change dramatically generally. The power system shows linear characteristics most of the time and thus ARX-structured method may have merit in bulk power grid modeling [24]. However, when a series of disturbances are increasingly stressing the system, the system will become less and less stable so that the trained ARX model will tend to be less accurate to estimate the dynamic response under the changed topology, which will be reflected as the accuracy index becoming lower. The threshold for the instability early warning was obtained when the system under the marginally stable situation after cascading outage. Marginally stable means the system is pushed to the edge of the stability, no matter how small a disturbance is added to this system, the system will collapse. The threshold is the estimation accuracy index of the marginally stable case.

Guideline for instability early warning

While a series of disturbances are increasingly stressing the system, degradation of its stability margin may finally lead to the system collapse. Continuous measurements on the monitored variables at a high sampling rate enable the ARX dynamic model to estimate the dynamic response in real time, and the model accuracy index obtained from the ARX dynamic model can indicate the decreasing of the stability margin. Therefore, a precisely defined threshold for instability early warning is necessary. Incidents of instability on a power system are not many, but they generally are accompanied by severe consequences. Therefore, the off-line dynamic simulation is the most convenient way to derive the threshold of the model accuracy index.

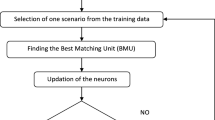
The method developed to assess potential system instability is described in Fig. 1. The basic steps of this flowchart are:

Fig. 1
figure 1

Flowchart for system instability assessment

Full size image
  1. (1)

    For a specific critical area, create N marginally stable simulation cases using a sequence of line faults.

  2. (2)

    For each simulation case, find the interface of the critical area and choose the input and out channel in each side of the interface, respectively. Then develop an ARX model using a period of system response data following the first disturbance.

  3. (3)

    After obtaining such a model, the system responses following the rest of the disturbance sequence are applied to the model to perform the response estimation.

  4. (4)

    Accuracy index values are obtained after disturbances.

  5. (5)

    Repeat Step (2), (3) and (4) for N marginally stable cases.

  6. (6)

    The threshold could be determined as the largest accuracy index of the last disturbance before collapse in all the N marginally stable cases.

  7. (7)

    Using the developed model to estimate the system response, if the accuracy index is equal or smaller than the threshold, a warning signal indicating potential instability following the next disturbance will be generated.

Case study for system instability early warning

Section III illustrated the proposed accuracy index threshold derivation process. To validate the idea of using the model accuracy index to early warn potential instability, an equivalent 179-bus WECC model [25] is used as the test system, as shown in Fig. 2. This model is simplified but retains the main dynamics of the entire WECC system.

Fig. 2
figure 2

WECC 179-bus model and disturbance locations

Full size image

Marginally stable case

Marginally stable means the system is pushed to the edge of the stability, no matter how small a disturbance is added to this system, the system will collapse [7].

Using the same approach as in [7] to create the marginally stable cases, a sequence of three-phase line faults is used in this case to drive the interface between area “0” and “1” to its marginally stable point. As an example, a marginally stable case is created by five faults occurring at different locations (C1, C2, C3, C4 and C5 in Fig. 2). The first four clearing time of line faults was fixed (five cycles), and the last one was adjusted to make this case to be marginally stable, which means the system would collapse if the clearing time of the last fault increase by 0.001 s. A lot a simulation cases were carried out using this method, only eight marginally instable cases can be created. Please note that each fault is cleared by opening the fault line. They increasingly weaken the interface but do not break the connection. This case can increasingly stress the operating condition (weakening the topology around that interface) by series of permanent faults.

The bus frequency, voltage magnitude and power angle simulation results in one marginally stable case are shown in Fig. 3. From Fig. 3, after five contingencies, the system has not caused a collapse yet. However, it has been pushed to its marginally collapse point, because if the clearing time of the last fault is increased by 0.001 s, the system would lose transient stability right after the last fault (in Fig. 4). Therefore, the interface between area “0” and “1” has been pushed to its marginally stable point.

Fig. 3
figure 3

Dynamics response of marginally stable case. a Voltage dynamic response after disturbance. b Frequency dynamic response after disturbance. c Power angle dynamic response after disturbance

Full size image
Fig. 4
figure 4

Dynamic responses of 29 generator buses. a Voltage dynamic response after disturbance. b Frequency dynamic response after disturbance. c Power angle dynamic response after disturbance

Full size image

Threshold for instability early warning

A threshold is needed to alert the system operator in order to prevent the system being pushed to instability. The proposed threshold determination method is applied in this section by investigating the instability problem between areas “0” and other areas.

Case study and results

In this study, the inputs of the ARX model is located in area “0” and the output is located in area “1”, which are shown in Fig. 2. The first disturbance is the three phase line fault occurred between area “0” and area “1” at location “C1” marked in Fig. 1, which is used to train the ARX model and obtain the first accuracy index of the model. Then four disturbances occur in every 40 s at different locations (C2, C3, C4 and C5 in Fig. 2) following the first disturbance. Frequency dynamic response after every disturbance is obtained and the accuracy index is calculated at the same time. The estimation results and accuracy index calculation results are shown in Fig. 5.

Fig. 5
figure 5

Dynamic response and accuracy index after contingency

Full size image

As shown in Fig. 5, the system tends to be less and less stable as more line disconnection disturbances added into the system, which is accompanied by the accuracy index of the system dynamic response decreasing, which indicates that the model accuracy index can be used to indicate the system stability to some extent.

In order to obtain the threshold of the accuracy index for transient instability early warning, a lot of simulation case studies were carried out, here a set of eight scenarios was created to provide a comprehensive coverage of stability performance of the power system. The variation trends of accuracy indices following the sequences of disturbances in eight scenarios are shown in Fig. 6

Fig. 6
figure 6

Accuracy variation trends following the sequences of disturbances in 8 cases

Full size image

.

Most of the accuracy indices in all the cases decrease due to the sequences of disturbances in Fig. 6. The difference of the disturbance location may be the main factor for special case 4 and case 8 why did not keep decreasing all the time. For all the simulation cases, after the fifth disturbance, the system is pushed to be marginally stable and most of the accuracy index also reaches its lowest point at the same time. The threshold can be obtained by the majority situations. It should be noted that this is a preliminary investigation on threshold value determination for system transient instability early warning. More studies need to be done to obtain further insight into the relationship between accuracy indices and potential instability for future work. The study in this paper is only an example to show how to derive the threshold with the proposed method.

For step 6 of the method described above, the threshold for this particular application is suggested as 0.44, the largest accuracy index value before collapses, as shown in Fig. 6. It means when the accuracy index reached 0.44, the system is almost stressed to its marginally instable point. For other cases, events with accuracy indices less than 0.44 are not necessarily instable, however, severe enough to alert for potential instability. This particular threshold selection method here only gives a “safe zone” of system operation, which means that no emergency control action is necessary if the index is higher than this threshold.

Conclusion

A measurement-based power system instability early warning index was proposed. The verification results prove that the proposed index can indicate the potential instability of the system. The preliminary results have shown that the instability threshold can be used to early warn the instability caused by cascading outages. Future work will focus on how to prove the effectiveness of the measurement-based instability early warning approach theoretically and more studies to explore the possibility of the application in the real power system.