Abstract
The Tokai region of Japan is known to be a seismic gap area and is expected to be the source region of the anticipated Tokai earthquake with a moment magnitude of over 8. Interplate slow slip occurred from approximately 2001 and subsided in 2005 in the area adjacent to the source region of the expected Tokai earthquake. Eight years later, the Tokai region again revealed signs of a slow slip from early 2013. This is the first evidence based on a dense Global Positioning System network that Tokai long-term slow slips repeatedly occur. Two datasets with different detrending produce similar transient crustal deformation and aseismic slip models, supporting the occurrence of the Tokai slow slip. The center of the current Tokai slow slip is near Lake Hamana, south of the center of the previous Tokai slow slip. The estimated moments, which increase at a roughly constant rate, amount to that of an earthquake with a moment magnitude of 6.6. If the ongoing Tokai slow slip subsides soon, it will suggest that there are at least two different types of slow slip events in the Tokai long-term slow slip area: that is, a large slow slip with a moment magnitude of over 7 with undulating time evolution and a small one with a moment magnitude of around 6.6 with a roughly linear time evolution. Because the Tokai slow slip changes the stress state to one more favorable for the expected Tokai earthquake, intense monitoring is going on.
Similar content being viewed by others
Background
The Tokai region in Japan is located near the Suruga trough, where the Philippine Sea plate subducts in the northwest direction beneath the Amurian plate at an annual rate of 2–3 cm/year (Sella et al. 2002) (Fig. 1). Because of the subduction of the Philippine Sea plate, large interplate earthquakes have repeatedly occurred in the Tokai region at time intervals of around 150 years (e.g., Kumagai 1996). The last Tokai earthquake occurred in 1854 (Richter magnitude M = 8.4). Currently, approximately 150 years have elapsed since the last Tokai earthquake. The Tokai region is deemed a seismic gap because it did not rupture at the time of the 1944 Tonankai earthquake [moment magnitude (M w) = 8.1] (Ishibashi 1981; Mogi 1981).
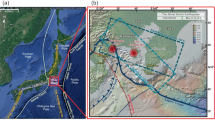
a Tectonic setting in and around Japan. Dashed lines indicate plate boundaries. Red solid lines show the fault patch adopted to estimate aseismic slip for the Tohoku and Tokai regions. Blue circles show the locations of the GPS sites used in the inversion of the first detrended dataset (see text). The T-direction and S-direction are denoted by black arrows (see text). Epicenters of the 2004 off Kii peninsula earthquakes are denoted by white circles. b Enlarged map of the Tokai region in a. Green arrows show the first detrended crustal movements (see text) for the period between January 1, 2013, and October 25, 2015, relative to the Misumi site. The red dashed line shows the source region of the anticipated Tokai earthquake or a seismic gap. The red solid line shows the fault patch adopted in the Tokai region to estimate aseismic slip. The T-direction and S-direction are denoted by black arrows (see text). Solid blue circles show the locations of the GPS sites used in the inversion of the second detrended dataset. Position time series of sites 996, 097, and 102 are shown in Figs. 2 and 6. The position time series of site 303 is shown in Additional file 1
In this tectonic setting, the dense Global Positioning System (GPS) network (GEONET) in Japan detected transient movements in the Tokai region from early 2001, which disappeared around 2005 (e.g., Ozawa et al. 2002; Miyazaki et al. 2006; Liu et al. 2010). This transient was interpreted as a long-term slow slip on the plate interface near Lake Hamana, central Japan, adjacent to the Tokai seismic gap (e.g., Ozawa et al. 2002; Ohta et al. 2004; Miyazaki et al. 2006; Liu et al. 2010; Tanaka et al. 2015). The previous Tokai slow slip gradually stopped and did not trigger the anticipated Tokai earthquake. After the discovery of the Tokai slow slip by GEONET, it was proposed that the Tokai long-term slow slip occurred during the periods of approximately 1978–1983 and 1987–1991 on the basis of baseline measurements by an electromagnetic distance meter or based on leveling data (e.g., Kimata et al. 2001; Ochi 2014). This hypothesis is consistent with other slow slip events around Japan, such as the Bungo slow slip and the Hyuga-nada slow slip (e.g., Ozawa et al. 2013; Yarai and Ozawa 2013), in that they have occurred quasi-periodically.
Since the 2011 M w9 Tohoku earthquake, eastward postseismic deformation has been the dominant source of crustal deformation in the Tokai region (see Fig. 1b). Around 12 years after the start of the previous Tokai slow slip, GEONET has been detecting a similar transient signal in the Tokai region since early 2013, which is mixed with the postseismic deformation due to the 2011 Tohoku earthquake. This transient movement suggests the possibility of the restart of the Tokai slow slip on the interface between the Amurian plate and the Philippine Sea plate. In addition to the crustal deformation detected by GEONET, a strain meter in the Tokai region also shows transient deformation (Miyaoka and Kimura 2016).
Because there is a possibility that the ongoing slow slip will lead to the anticipated Tokai earthquake, it is important to monitor the state of the current Tokai slow slip. In this study, we estimate the spatial and temporal evolution of the possible Tokai slow slip by applying square-root information filtering following the time-dependent inversion technique and compare it with the previous event. We also discuss the relationship between the low-frequency earthquakes and the estimated slow slip model and the influence of the latter on the expected Tokai earthquake.
Methods
GPS data were analyzed to obtain daily positions with Bernese GPS software (version 5.0). We adopted the F3 solution (Nakagawa et al. 2008), which uses the final orbit and earth rotation parameters of the International GNSS Service (IGS) and provides a higher S/N ratio than the previous F2 position time series (Hatanaka et al. 2003). We used the east–west (EW), north–south (NS), and up–down (UD) components at approximately 400 GPS sites in the Tokai, Kanto, and Tohoku regions.
Postseismic deformation due to the 2011 Tohoku earthquake has strong potential to contaminate and bias our search for slow slip in the Tokai region. We therefore attempt to remove its influence in two different ways, each generating a different dataset. First, we invert two fault patches (one for the Tokai slow slip and one for the Tohoku afterslip). In this analysis, we attributed all the postseismic deformation of the Tohoku earthquake to afterslip on the plate interface in the Tohoku region and did not take viscoelastic relaxation into account. This first approach assumes that the postseismic deformation due to viscoelastic relaxation can be partly modeled by afterslip modeling. However, it is a fact that viscoelastic relaxation contributes to the postseismic deformation due to the Tohoku earthquake (e.g., Sun et al. 2014). Thus, we need another approach to estimate the effects of viscoelastic relaxation and afterslip on the plate interface to support the results of the analysis with two fault patches. For this purpose, second, we attempt to remove the Tohoku postseismic deformation by considering exponential and logarithmic trends in the position time series in the analysis with one fault patch for the Tokai slow slip.
Analysis with two fault patches
In the analysis with two fault patches, we estimated and removed annual components separately from the EW, NS, and UD raw position time series at each station using a polynomial function corresponding to the trend component and trigonometric functions corresponding to the periodic annual components. Because the antenna was changed in 2012, we estimated different annual components before and after January 1, 2013, for the data from January 1, 2012, to October 25, 2015, using the following functions.
Here, Y(t) is the position time series, t is time, A i are the coefficients of the polynomial functions, and B i , C i , D i , and E i are the coefficients of the trigonometric functions.
The degree of the polynomial functions n and the overtone of the trigonometric functions m were estimated on the basis of Akaike information criterion (AIC) (Akaike 1974). After removing the annual components, we estimated the linear trend for the data between January 1, 2008, and January 1, 2011, during which no transient displacements occurred, and removed it from the data without annual components. We consider that the adopted steady state for this period is satisfactory for emphasizing the results, because the previous 2001–2005 slow slip and the current slow slip were clearly detected as a deviation from this adopted steady state. After this detrending, we smoothed the position time series by averaging over 3 days to reduce errors. Thus, this first detrending does not take into account the postseismic deformation due to the 2011 Tohoku earthquake, which is the main difference from the following second detrended dataset. We call this dataset the first detrended dataset.
We applied square-root information filtering (Ozawa et al. 2012) to the first detrended dataset following the inversion technique of McGuire and Segall (2003) for the period between January 1, 2013, and October 25, 2015. To reduce the computational burden, we used position time series with an interval of 3 days. Because we used detrended data, the estimated aseismic interplate slip is the deviation from the steady state for the period between January 1, 2008, and January 1, 2011.
We used 389 GPS sites in the filtering analysis for the first detrended dataset (see Fig. 1a). We weighted the EW, NS, and UD displacements with a ratio of 1:1:1/3 considering the standard deviations estimated from ordinary Kalman filtering.
We used two fault patches for the upper boundary of the Pacific plate along the Japan Trench and that of the Philippine Sea plate along the Suruga trough (Fig. 1). Because postseismic deformation occurred after the 2011 Tohoku earthquake as mentioned above, we attributed the cause of all postseismic deformation to afterslip on the Tohoku fault patch. In this case, we do not take the viscoelastic response due to the Tohoku earthquake into account because we consider that the effect of the viscoelastic response to ground deformation occurs on a spatially large scale and is similar to the afterslip effect at this point. That is, the contribution of the viscoelastic response to the surface deformation in the Tokai region may be partly compensated by our afterslip model on the first fault patch, which is the upper surface of the Pacific plate after the Tohoku earthquake.
We incorporated the inequality constraint that the slip is within 40° of the direction of the plate motion following the method of Simon and Simon (2006). In this filtering analysis, we incorporated the spatial roughness of the slip distribution (McGuire and Segall 2003). Hyperparameters that scale the spatial and temporal smoothness were estimated by approximately maximizing the log-likelihood of the system (Kitagawa and Gersch 1996; McGuire and Segall 2003). The optimal values of the spatial and temporal smoothness of the Tohoku fault patch are approximately 1.0 and 0.001, while those of the Tokai fault patch are approximately 0.004 and 0.001, respectively.
In the above analysis, a fault patch and a slip distribution on a fault patch are represented by the superposition of spline functions (Ozawa et al. 2001). The fault patch for the Tokai region consists of 11 nodes in the T-direction and 15 nodes in the S-direction (see Fig. 1b) (Ozawa et al. 2001). These directions are defined in Fig. 1b. The spacing of knots on the fault patch is approximately 20 km in the Tokai region. The plate boundary model is from Hirose et al. (2008). With regard to the fault patch in the Tohoku region, we used 12 nodes in the T-direction and 10 nodes in the S-direction with spacing of approximately 80 and 40 km in the T-direction and S-direction, respectively (see Fig. 1a). This Tohoku fault patch is used only in the analysis with two fault patches. Although the spacing between the parallel trench nodes is larger than that between the normal trench nodes, the results for the afterslip on this Tohoku fault patch are similar to those of Ozawa et al. (2012), in which the grid spacing is shorter. Thus, we consider that the fault patch adopted for the Tohoku region can satisfactorily describe the afterslip of the Tohoku earthquake. The plate boundary model is from Nakajima and Hasegawa (2006) and Nakajima et al. (2009). The coefficients of the spline functions that represent the slip distribution on the fault patches are estimated in this inversion (Ozawa et al. 2001).
Analysis with one fault patch
In the second detrending, we assumed that the postseismic deformation after the 2011 Tohoku earthquake follows a time evolution with exponential and logarithmic decay, because the causes of the postseismic deformation due to the 2011 Tohoku earthquake seem to be afterslip and viscoelastic relaxation (e.g., Sun et al. 2014). Theoretically, exponential decay corresponds to the viscoelastic relaxation in a medium with linear viscoelasticity, and logarithmic decay corresponds to the afterslip on a plate boundary with a rate- and state-dependent friction law (e.g., Hetland and Hager 2006; Marone et al. 1991). Tobita and Akashi (2015) first proposed that the postseismic deformation due to the 2011 Tohoku earthquake can be well reproduced by a function consisting of logarithmic and exponential functions. In this case, we first produced a dataset without annual components or the linear trend from the raw data in the same way as for the first detrended dataset, although we estimated annual components between January 1, 1997, and January 1, 2011. In this estimate of annual components, the 2001–2005 Tokai slow slip does not affect the results. The linear trend is estimated for the same period as for the first detrended dataset. After this process, we estimated the logarithmic and exponential components for the period between March 12, 2011, and March 11, 2013, assuming that the crustal deformation for this period was caused by the afterslip and viscoelastic relaxation due to the Tohoku earthquake and the local Tokai transient starting from early 2013. We regressed the following function to the position time series, as was first conducted by Tobita (2016):
where t, t1, and t2 are the time elapsed from the 2011 Tohoku earthquake on March 11, 2011, and the time constants of logarithmic and exponential decay, respectively. The time constants t1 and t2 of the logarithmic and exponential components were estimated from the position time series of four GPS sites in the Tohoku and Kanto regions of Japan (Tobita 2016). After the estimates of the time constants, we estimated A, B, and C in Eq. (3) and deleted the logarithmic and exponential components from all the position time series on the assumption that the time constants are the same among all the GPS position time series. With regard to the remaining annual components due to the changes to the antenna in 2012, we estimated them from the data for the period between 2012 and 2015 by employing a different annual component before and after January 1, 2013. We removed this annual component, as for the case of the first detrended dataset, so that we could compare the first and second detrended datasets. We call this detrended dataset the second detrended dataset from now.
We used 129 GPS sites in the Tokai region of the second detrended dataset for the time-dependent inversion analysis (Fig. 1b). This is because it is not necessary to take into account the postseismic deformation due to the 2011 Tohoku earthquake for the second detrended dataset, although we have to take it into account in the first detrended dataset.
In the second detrended dataset, we used the same fault patch between the Philippine Sea plate and the Amurian plate beneath the Tokai region as that in the first detrended dataset without the Tohoku fault patch, because we consider that the effects of the viscoelastic relaxation and afterslip due to the 2011 Tohoku earthquake are nonexistent in the second detrended dataset owing to the removal of the exponential and logarithmic trends.
The spatial and temporal smoothness of the second detrended dataset is set to the same values as those of the Tokai fault patch in the analysis with two fault patches so that we can approximately compare the results of this analysis with those of the analysis with two fault patches.
Analysis of the previous Tokai slow slip
In addition, we created a third detrended dataset using the same method as for the first detrended dataset but with a different period of estimation for the annual components. That is, we estimated the annual components of the EW, NS, and UD position time series separately for the period up to January 1, 2011, together with a polynomial function from the raw position time series at each station. We estimated the linear trend for the same period as for the first and second datasets and removed it from the position time series without annual components. We used 86 GPS sites in the following inversion. Using this third detrended dataset, we estimated an approximate model of the previous Tokai slow slip for the period between January 1, 2001, and January 1, 2008, by the same method as for the second detrended dataset because there are no other signals, such as those corresponding to postseismic deformation due to the 2011 Tohoku earthquake, for this period. We consider that the postseismic deformation due to the 2004 off Kii peninsula earthquakes (M w > 7) (see Fig. 1a) does not significantly affect the previous Tokai slow slip model. The estimated optimal spatial and temporal parameters are approximately 3.0 and 1.0, respectively.
Results and discussion
Analysis with two fault patches
The first detrended crustal deformation data show eastward displacements relative to the Misumi site (Fig. 1b). The time evolution of these eastward displacements can be clearly observed in the first detrended position time series of selected GPS sites (Fig. 2a–c). The eastward displacements are mostly attributed to the postseismic deformation due to the 2011 Tohoku earthquake, although the Philippine Sea plate is subducting beneath the Amurian plate from the Suruga trough in the northwestward direction. However, there are also southward displacements of approximately 1 cm in the north–south position time series from early 2013 in Fig. 2a–c compared with approximately 2 cm eastward movements, which cannot be explained by either afterslip or viscoelastic relaxation due to the 2011 Tohoku earthquake, suggesting aseismic slip on the plate interface in the Tokai region. Thus, we assume that transient crustal deformation started locally from early 2013 at the latest in the Tokai region. We do not treat the southward transient movements before 2013 in the same time series in this paper, because the spatial pattern of this change before 2013 is less clear than that of the transient movements after 2013.
(Top) First detrended position time series (see text) at sites a 996, b 097, and c 102, whose locations are shown in Fig. 1b. EW, NS, and UD represent east–west, north–south, and up–down components, with eastward, northward, and upward positive, respectively. The offset in 2011 indicates coseismic deformation from the 2011 Tohoku earthquake. Red lines show values computed by our best-fitting interplate aseismic slip model, which consists of two fault patches for the upper boundary of the Pacific plate along the Japan Trench and that of the Philippine Sea plate along the Suruga trough. (Bottom) Position time series at sites d 996, e 097, and f 102 with the computed values of the estimated optimal Tohoku afterslip model removed from the first detrended position time series to make the transient from the Tokai slow slip clear. The red line shows values computed from the Tokai slow slip model
Although we estimated the afterslip on the Pacific plate in the Tohoku region together with the slip on the Philippine Sea plate in the Tokai region, we will not discuss it in this paper because our focus is on the Tokai slow slip. The characteristic features of the estimated afterslip on the Pacific plate in the Tohoku region are similar to the results of Ozawa et al. (2012) (Additional file 2).
Figure 2d–f shows position time series with the effect of the Tohoku afterslip model removed from the first detrended dataset to make the Tokai transient clear. That is, we calculated the contribution to the ground displacements from the optimal Tohoku afterslip model estimated in this study and subtracted it from the first detrended position time series. We consider that Fig. 2d–f may be directly comparable to the second dataset. All the GPS sites in Fig. 2d–f show southeastward or eastward displacements from early 2013. Figure 3 shows the characteristic features of the spatial patterns of the data derived by removing the component of the 2011 Tohoku afterslip model estimated in this research from the first detrended dataset for the period between January 1, 2013, and October 25, 2015. In this figure, we can observe southeastward crustal deformation west of Lake Hamana and eastward deformation east of Lake Hamana, strongly indicating the occurrence of aseismic interplate slip near Lake Hamana. Furthermore, the vertical crustal deformation shows uplift east of Lake Hamana for the same period (Fig. 3a), which is also expected to result from a slow slip near Lake Hamana. The 1σ error is 1–2 mm for horizontal displacements and 3–6 mm for vertical displacements in Fig. 3a, as estimated by ordinary Kalman filtering. Thus, the observed transients in Fig. 3a exceed the 1σ error. We do not consider that the postseismic deformation due to the 2011 Tohoku earthquake could have created the pattern in Fig. 3a by viscoelastic relaxation or afterslip on the Pacific plate. This is because this pattern occurs in a spatially small scale in the Tokai region compared with the viscoelastic relaxation and afterslip on the Pacific plate, which probably causes spatially larger-scale ground deformation because the source is so far from the ground surface in the Tokai region. Furthermore, afterslip or viscoelastic relaxation could not have created the uplift near Lake Hamana.
a Horizontal crustal deformation, which was obtained by subtracting the effect of the afterslip model of the Tohoku earthquake from the first detrended crustal deformation data to make the transient from the Tokai slow slip clear. The period is between January 1, 2013, and October 25, 2015. Arrows show the movements of the GPS sites. The color indicates the spatially smoothed vertical displacement. b Crustal deformation computed from our best-fitting Tokai slow slip model based on the first detrended dataset. Arrows show the computed horizontal displacements, while the color indicates the computed vertical displacement
On the basis of the observed first detrended displacements, our filtering analysis shows a slow slip area near the west boundary of the source region of the expected Tokai earthquake (Fig. 4a–c) as expected from Fig. 3a. The aseismic interplate southeastward slip rate from January 1, 2013, to January 1, 2014, amounts to 1 cm/year in Fig. 4a and is centered near Lake Hamana. The maximum aseismic interplate slip rate for the period between January 1, 2014, and January 1, 2015, exceeds 2 cm/year in Fig. 4b. Figure 4c shows an aseismic interplate slip rate of approximately 1–2 cm/year near Lake Hamana for the period between January 1, 2015, and October 25, 2015. The aseismic slip in the Nagoya area in Fig. 4c is less reliable because it is located near the western boundary of the fault patch used in the modeling, and the estimated error is relatively large in this area. The time evolution of the slip area indicates that the center of the aseismic slip is near Lake Hamana, and movement of the center of the slip area is not observed. Figure 4d–f shows the 1σ error of the estimated aseismic slip rate with a contour interval of 2 mm/year, indicating that the estimated interplate slip rates for all the periods are larger than the 1σ error. The main area in which the estimated total slip is in the southeastward direction is located on the west boundary of the seismic gap, and the slip magnitude surpasses 4 cm for the period between January 1, 2013, and October 25, 2015, with a moment magnitude exceeding 6.6 (Fig. 5a, b). The estimated moment release rate seems to be roughly constant in Fig. 5b from a long-term viewpoint. The horizontal and vertical displacements computed from our best-fitting Tokai aseismic slip model based on the first detrended dataset reproduce the observed crustal deformation well, as shown in Figs. 2 and 3b.
(Top) Estimated aseismic slip rate on the interface between the Amurian plate and the Philippine Sea plate based on the first detrended dataset for the periods between a January 1, 2013–January 1, 2014, b January 1, 2014–January 1, 2015, and c January 1, 2015–October 25, 2015, with a contour interval of 1 cm/year (red lines). The red arrows also indicate the estimated aseismic slip rate. The dashed lines indicate isodepth contours of the plate interface with an interval of 20 km (Hirose et al. 2008). The blue dashed line shows the source region of the anticipated Tokai earthquake. Green dots indicate epicenters of low-frequency earthquakes determined by Japan Meteorological Agency for the same period. Thin solid lines indicate prefectural boundaries in Japan. (Bottom) Estimated 1σ error with a contour interval of 2 mm/year. d–f The periods of a–c
a Estimated aseismic slip based on the first detrended dataset for the period between January 1, 2013, and October 25, 2015, shown by red contours with an interval of 2 cm. The red arrows also indicate the estimated aseismic slip. The nomenclature is the same as that in Fig. 4a. b Time evolution of the estimated moment of the current Tokai slow slip based on the first detrended dataset. Dashed lines indicate the 3σ error
Analysis with one fault patch
Figure 6a–c shows the position time series with the annual components and the linear trend removed from the raw data, as described in detail in the subsection on the analysis with one fault patch in the “Methods” section, and the values computed using an optimal function consisting of logarithmic and exponential functions. The second detrended dataset is shown for the same selected GPS sites in Fig. 6d–f. In Fig. 6d–f, we can clearly observe southeastward and eastward residuals from early 2013. Figure 7a shows the spatial pattern of the second detrended dataset for the period between January 1, 2013, and October 25, 2015. The observed spatial pattern of the second detrended dataset shows southeastward displacements west of Lake Hamana and eastward displacements east of Lake Hamana. Uplift is observed near Lake Hamana. The 1σ error ranges from 1 to 2 mm for the horizontal components and from 3 to 6 mm for the vertical components. These features are similar to those in Fig. 3a for the first detrended dataset without the Tohoku afterslip effects. The filtering analysis of the second detrended dataset shows an area of aseismic slip centered on Lake Hamana (Fig. 8a–c), which is similar to the slip area estimated from the first detrended dataset in Fig. 4. Furthermore, the slip rate magnitude seems to be very similar to that obtained by analysis using the first detrended dataset, ranging from 1 to 2 cm/year (Fig. 8a–c). We cannot observe any significant movements of the center of the slow slip area for the entire period. Figure 8d–f shows that the estimated aseismic slip rates in Fig. 8a–c are larger than the 1σ error. The total slip magnitude amounts to more than 4 cm for the period between January 1, 2013, and October 25, 2015, with a moment magnitude reaching 6.6 (Fig. 9a, b). This model closely reproduces the observed transient deformation shown in Figs. 6d–f and 7a, b.
(Top) Position time series with the linear trend estimated for the period between January 1, 2008, and January 1, 2011, and annual components estimated between January 1, 1997, and January 1, 2011, removed from the raw data (see text) at sites a 996, b 097, and c 102. The nomenclature is the same as that in Fig. 2. Red lines show values computed by our best-fitting function consisting of logarithmic and exponential functions (see text). (Bottom) Second detrended position time series at sites d 996, e 097, and f 102 (see text). The green line shows values computed from the Tokai slow slip model based on the second detrended dataset
a Second detrended crustal deformation for the period between January 1, 2013, and October 25, 2015. Arrows show the horizontal movements of the GPS sites. The color indicates the spatially smoothed vertical displacement. b Crustal deformation computed from our best-fitting Tokai slow slip model based on the second detrended dataset. Arrows show the computed horizontal displacements, while the color indicates the computed vertical displacement
(Top) Aseismic slip rate estimated from the second detrended dataset on the interface between the Amurian plate and the Philippine Sea plate for the periods between a January 1, 2013–January 1, 2014, b January 1, 2014–January 1, 2015, and c January 1, 2015–October 25, 2015, with a contour interval of 1 cm/year (red lines). The red arrows also indicate the estimated aseismic slip rate. The nomenclature is the same as that in Fig. 4a. (Bottom) Estimated 1σ error with a contour interval of 2 mm/year. d–f The periods of a–c
a Aseismic slip based on the second detrended data for the period between January 1, 2013, and October 25, 2015, shown by red contours with an interval of 2 cm. The red arrows also indicate the estimated aseismic slip. The nomenclature is the same as that in Fig. 5a. b Time evolution of the estimated moment of the current Tokai slow slip based on the second detrended dataset. Dashed lines indicate the 3σ error
Comparison between the two models
We obtained almost the same results using the two different detrended datasets. With regard to the estimated model based on the first detrended dataset, we cannot rule out the existence of a systematic error resulting from the postseismic deformation since the 2011 Tohoku earthquake. However, we believe that any such systematic error would be small considering the difference in the spatial scale of the viscoelastic relaxation effect mentioned above. Furthermore, because our model based on the second detrended dataset, which excludes the exponential and logarithmic time evolution corresponding to viscoelastic relaxation and afterslip, respectively, shows similar results for the location and time evolution of aseismic slip to those obtained from the first detrended dataset, we consider that slow slip is now occurring on the west boundary of the Tokai seismic gap area, without signs of decay. This finding is consistent with the strain meter observations in this region by Japan Meteorological Agency, which also indicate interplate slow slip near Lake Hamana (Miyaoka and Kimura 2016). Although the start time of the current slow slip event is unclear, we assumed that it started in early 2013 at the latest on the basis of the approximate start time of the transient in Figs. 2 and 6 and the moment release rate shown in Figs. 5b and 9b. For the second detrended data, we also changed the regression periods for the logarithmic and exponential functions to March 12, 2011–March 12, 2012, and March 12, 2011–March 12, 2014, respectively, and found that the characteristic feature of a slip area appearing that was centered on Lake Hamana was not changed.
The reason why the two different detrended datasets gave similar results is that the postseismic deformation due to the 2011 Tohoku earthquake can be well explained by both the kinematic afterslip model and the logarithmic and exponential functions, which are based on the physics of the rate- and state-dependent friction law and viscoelasticity. However, it remains unclear why the kinematic afterslip model and the logarithmic and exponential functions produced similar postseismic deformation. We cannot rule out the possibility that the estimated logarithmic and exponential functions may reflect an actual process of afterslip and viscoelastic relaxation involved in the postseismic deformation due to the Tohoku earthquake. This problem remains to be solved in a future study.
Comparison between the previous and current slow slips
Interplate aseismic slip occurred in the Tokai region approximately during the period between 2001 and 2005. Figure 10 shows the spatial pattern of the third detrended dataset for the period between January 1, 2001, and January 1, 2008. As shown in Fig. 10, the spatial pattern of this transient deformation is very similar to that of the current Tokai transient (Figs. 3a, 7a). This strongly indicates that the current transient is a true signal caused by aseismic interplate slip in the Tokai region. The center of the previous slow slip area for the period between January 1, 2001, and January 1, 2008, is located between the low-frequency earthquake area and Lake Hamana, while the ongoing slow slip area is located in the southern part of the previous Tokai slow slip area (Ozawa et al. 2002; Ohta et al. 2004; Miyazaki et al. 2006; Liu et al. 2010; Ochi and Kato 2013) (see Fig. 11). Low-frequency earthquakes are accompanied by episodic slip on the plate interface (e.g., Shelly et al. 2006). The estimated moment magnitude (M w) of the previous event is over 7 and much larger than the values based on the two different detrended datasets (see Fig. 12).
a Third detrended crustal deformation for the period between January 1, 2001, and January, 1 2008. The color indicates the spatially smoothed vertical displacement. b Crustal deformation computed from the aseismic slip model at the time of the previous Tokai slow slip for the period between January 1, 2001, and January 1. 2008, which is shown in Fig. 11
Comparison of the estimated aseismic interplate slip. The gray contours show the slip magnitude of the previous Tokai slow slip for the period between January 1, 2001, and January 1, 2008, with a contour interval of 10 cm based on the third detrended data (see text). The red contours show the estimated aseismic slip based on the first detrended data (see text) for the period between January 1, 2013, and October 25, 2015. The black contours show the estimated aseismic slip based on the second detrended data for the period between January 1, 2013, and October 25, 2015. Green dots indicate the epicenters of low-frequency earthquakes for the period between January 1, 2001, and January 1, 2008. The other nomenclature is the same as that in Fig. 5a
Estimated time evolution of moment release. Line 1 indicates the estimated moment of the previous Tokai slow slip. Lines 2 and 3 indicate the estimated moments based on the first and second detrended datasets, respectively. We set the start time to 2013 for Lines 2 and 3 to match the start time of 2001 for the previous Tokai slow slip
Because the previous Tokai slow slip reached a moment magnitude of over 7, we cannot rule out the possibility that the present stage may correspond to the initial stage of the time evolution of the Tokai slow slip. The estimated moment release of the current Tokai slow slip seems to have increased almost linearly since early 2013, as shown in Figs. 5b and 9b and in Fig. 12 in the long term, while the moment release rate of the previous Tokai slow slip changed in the long term. At this point, the current Tokai slow slip seems to be following a different time evolution from that in the previous event (Fig. 12).
At the time of the previous Tokai slow slip, the center of the slip area was located near Lake Hamana in the early period, then moved north over time (e.g., Ozawa et al. 2001; Miyazaki et al. 2006) (see Additional file 3). Thus, there is a possibility that the ongoing slow slip will move northward over time with an increase in the slip magnitude. However, if the current aseismic slip stops in the near future, it will indicate the coexistence of relatively small slow slip events in the Tokai long-term slow slip area. Our previous Tokai slow slip model reproduces the observations well as shown in Fig. 10.
Relationship with low-frequency earthquakes
Non-volcanic low-frequency tremors have been discovered in the Nankai trough subduction zone in Japan (Obara 2002). These low-frequency tremors include low-frequency earthquakes whose hypocenters can be determined by identification of coherent S-wave and P-wave arrivals (Katsumata and Kamaya 2003). Low-frequency earthquakes occur at a depth of approximately 30–40 km on the plate interface in the Tokai region. Low-frequency tremors that contain low-frequency earthquakes occur in the Tokai region with a recurrence interval of approximately 6 months accompanied by aseismic slip, which continues for 2–3 days, and release a seismic moment corresponding to M w ~ 6 (Hirose and Obara 2006). This relationship between low-frequency tremors or earthquakes and slow slip events has also been observed in many other areas (e.g., Rogers and Dragert 2003; Shelly et al. 2006). Thus, we can expect low-frequency tremors or earthquakes with higher activity owing to the influence of the current Tokai slow slip. However, such a relationship has not been observed this time, although there was a correlation between the low-frequency earthquake activity in the Tokai region and the previous Tokai slow slip (Ishigaki et al. 2005). We consider that low-frequency earthquakes are not being activated by the current slow slip because the central part of the slow slip area is located away from the low-frequency earthquake area (Figs. 5a, 9a) and its magnitude is still small, suggesting little change in the stress in the low-frequency earthquake area. Although short-term slow slip events of M w6 in the Tokai region trigger low-frequency tremors or earthquakes (Hirose and Obara 2006), the area of induced low-frequency tremors or earthquakes overlaps with the short-term slow slip area, indicating a large change in stress in this case.
The short-term slow slip with a maximum moment magnitude of M w6 in the low-frequency earthquake area (Hirose and Obara 2006) does not affect our optimal Tokai slow slip model owing to its small moment magnitude compared with the current Tokai event and the center location of our current Tokai model.
Influence on the expected Tokai earthquake
There is a possibility that the 2011 Tohoku earthquake and its postseismic deformation have affected the seismic activity of the Japanese archipelago. In studies on the Coulomb failure stress change (ΔCFS) due to the Tohoku earthquake, Toda et al. (2011) showed seismic excitation throughout central Japan after the Tohoku earthquake and Ishibe et al. (2015) reported changes in seismicity in the Kanto region that were correlated with ΔCFS. Furthermore, slow slip events off the Boso peninsula, east Japan, have shown a shorter recurrence interval after the Tohoku earthquake (Ozawa, 2014). Our Tohoku coseismic model (Ozawa et al. 2012) produces a ΔCFS of approximately 3 kPa near Cape Omaezaki in the Tokai seismic gap. Furthermore, the two estimated models of the current Tokai slow slip produce ΔCFS of approximately 3 kPa near Cape Omaezaki (see Fig. 1b). We assumed a rigidity of 30 GPa, Poisson’s ratio of 0.25, and a friction coefficient of 0.4 in these calculations (Harris 1998). Considering these points, we cannot rule out the possibility that the ongoing slow slip will trigger the anticipated Tokai earthquake, although the previous event did not cause the expected earthquake. Thus, it is very important to intensively monitor the ongoing Tokai slow slip using the dense GPS network in Japan.
Conclusions
It has been proposed that the Tokai slow slip occurs with a recurrence interval of 9–14 years, although the truth of this hypothesis is difficult to establish because of the scarcity of data (e.g., Kimata et al. 2001; Ochi 2014). Thus, our finding, obtained using the dense GPS network in Japan, confirms that the Tokai slow slip has occurred repeatedly on the west boundary of the Tokai seismic gap and changed the stress state in favor of the anticipated Tokai earthquake. Although the start time of the current event is not clear, the recurrence interval of the Tokai slow slip is approximately 12 years if we assume it to be early 2013. Our estimated models of the current Tokai slow slip indicate differences from the previous event regarding the following points. First, the magnitude of the current event is approximately 6.6, which is very small compared with the M w of over 7 for the previous event, and increasing at a roughly constant rate. Second, the center of the slip area is located south of that in the previous event. Third, the moment release rate is very small compared with that in the previous event. We cannot clearly state whether the current slow slip will become similar to the previous Tokai slow slip or whether it will be a different type of slow slip from the above points.
Abbreviations
- GPS:
-
Global Positioning System
References
Akaike H (1974) A new look at the statistical model identifications. IEEE Trans Autom Control 19:716–723
Harris RA (1998) Introduction to special section: stress triggers, stress shadows, and implications for seismic hazard. J Geophys Res 103:24347–24358
Hatanaka Y, Iizuka T, Sawada M, Yamagiwa A, Kikuta Y, Johnson JM, Rocken C (2003) Improvement of the analysis strategy of GEONET. Bull Geogr Surv Inst 49:11–37
Hetland EA, Hager BH (2006) The effects of rheological layering on post-seismic deformation. Geophys J Int 166:277–292
Hirose H, Obara K (2006) Short-term slow slip and correlated tremor episodes in the Tokai region, central Japan. Geophys Res Lett 33:L17311. doi:10.1029/2006GL026579
Hirose F, Nakajima J, Hasegawa A (2008) Three-dimensional seismic velocity structure and configuration of the Philippine Sea slab in southwestern Japan estimated by double-difference tomography. J Geophys Res 113:B09315. doi:10.1029/2007JB005274
Ishibashi K (1981) Specification of a soon-to-occur seismic faulting in the Tokai district central Japan based upon seismotectonics. In: Simpson DW, Richards PG (eds) Earthquake prediction. Maurice Ewing series, vol 4. American Geophysical Union, Washington, pp 297–332
Ishibe T, Satake K, Sakai S, Shimazaki K, Tsuruoka H, Yokota Y, Nakagawa S, Hirata N (2015) Correlation between Coulomb stress imparted by the 2011 Tohoku-Oki earthquake and seismicity rate change in Kanto, Japan. Geophys J Int 201:112–134
Ishigaki Y, Katsumata A, Kamaya N, Nakamura K, Ozawa S (2005) The relation between the slow slip of plate boundary in Tokai district and low frequency earthquakes. Q J Seismol 68:81–97
Katsumata A, Kamaya N (2003) Low-frequency continuous tremor around the Moho discontinuity away from volcanoes in the southwest Japan. Geophys Res Lett 30:1020. doi:10.1029/2002GL0159812
Kimata F, Hirahara K, Fujii N, Hirose H (2001) Repeated occurrence of slow slip events on the subducting plate interface in the Tokai region, central Japan, the focal region of the anticipated Tokai earthquake (M = 8). Paper presented at the AGU Fall Meeting, San Francisco, 10–14 December 2001
Kitagawa G, Gersch W (1996) Linear gaussian state space modelling. In: Kitagawa G, Gersch W (eds) Smoothness priors analysis of time series. Lecture notes in statistics, vol 116. Springer, New York
Kumagai H (1996) Time sequence and the recurrence models for large earthquakes along the Nankai Trough revisited. Geophys Res Lett 23:1139–1142
Liu Z, Owen S, Dong D, Lundgren P, Webb F, Hetland E, Simons M (2010) Integration of transient strain events with models of plate coupling and areas of great earthquakes in southwest Japan. Geophys J Int 181:1292–1312
Marone CJ, Scholtz CH, Bilham R (1991) On the mechanics of earthquake afterslip. J Geophys Res 96:8441–8452. doi:10.1029/91JB00275
McGuire JJ, Segall P (2003) Imaging of aseismic slip transients recorded by dense geodetic networks. Geophys J Int 155:778–788
Miyaoka K, Kimura H (2016) Detection of long-term slow slip event by strainmeters using the stacking method. Q J Seismol 79:15–23
Miyazaki S, Segall P, McGuire J, Kato T, Hatanaka Y (2006) Spatial and temporal evolution of stress and slip rate during the 2000 Tokai slow earthquake. J Geophys Res 111:B03409. doi:10.1029/2004JB003426
Mogi K (1981) Seismicity in western Japan and long-term earthquake forecasting. In: Simpson DW, Richards PG (eds) Earthquake prediction. Maurice Ewing series, vol 4. American Geophysical Union, Washington, pp 43–51
Nakagawa H, Miyahara B, Iwashita C, Toyofuku T, Kotani K, Ishimoto M, Munekane H, Hatanaka Y (2008) New analysis strategy of GEONET. In: Proceedings of international symposium on GPS/GNSS, Tokyo, 11–14 November 2008
Nakajima J, Hasegawa A (2006) Anomalous low-velocity zone and linear alignment of seismicity along it in the subducted Pacific slab beneath Kanto, Japan: reactivation of subducted fracture zone? Geophys Res Lett 33:L16309. doi:10.1029/2006GL026773
Nakajima J, Hirose F, Hasegawa A (2009) Seismotectonics beneath the Tokyo metropolitan area, Japan: effect of slab-slab contact and overlap on seismicity. J Geophys Res 114:B08309. doi:10.1029/2008JB006101
Obara K (2002) Nonvolcanic deep tremor associated with subduction in southwest Japan. Science 296:1679–1681. doi:10.1126/science.1070378
Ochi T (2014) Possible long-term SSEs in the Tokai area, central Japan, after 1981: size, duration, and recurrence interval. Paper presented at the AGU Fall Meeting, San Francisco, 15–19 December 2014
Ochi T, Kato T (2013) Depth extent of the long-term slow slip event in the Tokai district, central Japan: a new insight. J Geophys Res 118:4847–4860. doi:10.1002/jgrb.50355
Ohta Y, Kimata F, Sagiya T (2004) Reexamination of the interplate coupling in the Tokai region, central Japan, based on the GPS data in 1997–2002. Geophys Res Lett 31:L24604. doi:10.1029/2004GL021404
Ozawa S, Murakami M, Tada T (2001) Time-dependent inversion study of the slow thrust event in the Nankai trough subduction zone, southwestern Japan. J Geophys Res 106:787–802
Ozawa S, Murakami M, Kaidzu M, Tada T, Sagiya T, Hatanaka Y, Yarai H, Nishimura T (2002) Detection and monitoring of ongoing aseismic slip in the Tokai region, central Japan. Science 298:1009–1012
Ozawa S, Nishimura T, Munekane H, Suito H, Kobayashi T, Tobita M, Imakiire T (2012) Preceding, coseismic, and postseismic slips of the 2011 Tohoku earthquake, Japan. J Geophys Res 117:B07404. doi:10.1029/2011JB009120
Ozawa S, Yarai H, Imakiire T, Tobita M (2013) Spatial and temporal evolution of the long-term slow slip in the Bungo Channel, Japan. Earth Planets Space 65:67–73
Rogers G, Dragert H (2003) Episodic tremor and slip on the Cascadia subduction zone: the chatter of silent slip. Science 300:1942–1943
Sella GF, Dixon TH, Mao A (2002) REVEL: a model for recent plate velocities from space geodesy. J Geophys Res 107:ETG11-1–ETG11-30. doi:10.1029/2000JB000033
Shelly DR, Beroza GC, Ide S, Nakamula S (2006) Low-frequency earthquakes in Shikoku, Japan and their relationship to episodic tremor and slip. Nature 442:188–191. doi:10.1038/nature04931
Simon D, Simon DL (2006) Kalman filtering with inequality constraints for turbofan engine health estimation. IEE Proc Control Theory Appl 153:371–378
Sun T, Wang K, Iinuma T, Hino R, He J, Fujimoto H, Kido M, Osada Y, Miura S, Ohta Y, Hu Y (2014) Prevalence of viscoelastic relaxation after the 2011 Tohoku-oki earthquake. Nature 514:84–87. doi:10.1038/nature13778
Tanaka Y, Yabe S, Ide S (2015) An estimate of tidal and non-tidal modulations of plate subduction speed in the transient zone in the Tokai district. Earth Planets Space 67:141. doi:10.1186/s40623-015-0311-2
Tobita M (2016) Combined logarithmic and exponential function model for fitting postseismic GNSS time series after 2011 Tohoku-Oki earthquake. Earth Planets Space 68:41. doi:10.1186/s40623-016-0422-4
Tobita M, Akashi T (2015) Evaluation of forecast performance of postseismic displacements. Rep Coord Comm Earthq Predict 93:393–396 (in Japanese)
Toda S, Stein RS, Lin J (2011) Widespread seismicity excitation throughout central Japan following the 2011 M = 9.0 Tohoku earthquake and its interpretation by Coulomb stress transfer. Geophys Res Lett 38:L00G03. doi:10.1029/2011GL047834
Yarai H, Ozawa S (2013) Quasi-periodic slow slip events in the afterslip area of the 1996 Hyuga-nada earthquakes, Japan. J Geophys Res Solid Earth 118:2512–2527. doi:10.1002/jgrb.50161
Authors’ contributions
SO performed all the data analysis, prepared the graphical material, and wrote the manuscript. MT proposed the detrending method using a function consisting of logarithmic and exponential functions and estimated the time constants of the logarithmic and exponential functions. MT and HY supervised SO and helped to improve the manuscript. All authors read and approved the final manuscript.
Acknowledgements
We are grateful to our colleagues for helpful discussions. Prof. Teruyuki Kato of the Earthquake Research Institute, the University of Tokyo, advised us about detrending. Prof. Sagiya of Nagoya University provided us with helpful information. The hypocenter data of low-frequency earthquakes are from Japan Meteorological Agency. The data used in this paper are available by contacting ozawa-s96sa@mlit.go.jp.
Competing interests
The authors declare that they have no competing interests.
Author information
Authors and Affiliations
Corresponding author
Additional files
40623_2016_430_MOESM1_ESM.pdf
Additional file 1. (A) Third detrended position time series at site 303, whose location is shown in Fig. 1b. The red lines indicate the values computed from our best-fitting Tokai model. (B) Third detrended position time series at site 097, whose location is shown in Fig. 1b. The red lines indicate the computed values. (C) Third detrended position time series at site 102, whose location is shown in Fig. 1b. Our model reproduces the observations well.
40623_2016_430_MOESM2_ESM.pdf
Additional file 2. (Top) First detrended crustal deformation for the periods between (A) January 1, 2013 and January 1, 2014, (B) January 1, 2014 and January 1, 2015, and (C) January 1, 2015 and October 25, 2015. (Bottom) Estimated aseismic slip with a contour interval of 20 cm. (D–F) The periods of (A–C). All the estimated slip patterns are similar to the results of Ozawa et al. (2012).
40623_2016_430_MOESM3_ESM.pdf
Additional file 3. Estimated aseismic slip based on the third detrended dataset for the period (A) between January 1, 2001 and January 1, 2002. The red lines indicate the aseismic slip magnitude with a contour interval of 5 cm. The nomenclature is the same as that in Fig. 4a. We can see a relatively large slip area on the west boundary of the expected source region of the Tokai earthquake. (B) January 1, 2002–January 1, 2003. In this period, the slip area west of Lake Hamana disappears and the slip area north of Lake Hamana expands slightly. (C) January 1, 2003–January 1, 2004. The slip area north of Lake Hamana becomes large in this period. (D) January 1, 2004–January 1, 2005. In this period, the slip area expands to the southwest, which is attributed the postseismic deformation due to the 2004 off Kii-peninsula earthquakes with a moment magnitude of around 7.3–7.4 inside the Philippine Sea plate (Fig. 1a). Thus, we consider that this expansion of the slip area to the southwest is not reliable. (E) January 1, 2005–January 1, 2006. In this period, the aseismic interplate slip seems to be nearing its end. (F) January 1, 2006–January 1, 2007. (G) January 1, 2007–January 1, 2008. (H–N) Estimated 1σ error for the periods corresponding to (A–G).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ozawa, S., Tobita, M. & Yarai, H. A possible restart of an interplate slow slip adjacent to the Tokai seismic gap in Japan. Earth Planet Sp 68, 54 (2016). https://doi.org/10.1186/s40623-016-0430-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40623-016-0430-4