Abstract
There are different approaches that indicate the dynamic of the growth of microbe. In this research, we simulate the growth by utilizing the concept of fractional calculus. We investigate a fractional system of integro-differential equations, which covers the subtleties of the diffusion between infected and asymptomatic cases. The suggested system is applicable to distinguish the presentation of growth level of the infection and to approve if its mechanism is positively active. An optimal solution under simulation mapping assets is considered. The estimated numerical solution is indicated by employing the fractional Tutte polynomials. Our methodology is based on the Atangana–Baleanu calculus (ABC). We assess the recommended system by utilizing real data.
Similar content being viewed by others
1 Introduction
Integro-differential dynamic system of equations simulates various states from science and engineering corresponding to the analysis, control, and optimization studies. The main model in this direction is the Wilson–Cowan system, which designs the dynamics of connections between populations of very inhibitory system in cells or neurons. It was developed by Hugh R. Wilson and Jack D. Cowan [1]. The system and its generalizations have been extensively utilized in forming neuronal or cell populations [2]. The system is significant traditionally because it utilizes phase plane approaches and mathematical solutions to designate the reactions of neuronal populations to motivations. The general system involves simple integro-differential equations, therefore, limit cycle performance (neural fluctuations) and stimulus-dependent suggested reactions are expected. The key results contain the solvability of multiple stable situations and hysteresis in the population’s reaction.
Coronavirus (COVID-19) has been an infectious virus molded by a recently exposed coronavirus. It has been recorded by the World Health Organization (WHO), it is a pandemic. The first WHO warning of dyed-in-the-wool cases of COVID-19 indicated on January 2020 with 282 cases (see [3, 4]). There is an increasing number of research works that develop the growth of the COVID-19 infection by using an ordinary dynamic system [5] and fractal-fractional dynamic system [6]. Utilizing the recent information from European and African countries, Atangana and Araz presented numerous statistical analyses [7, 8]. Musa et al. [9] introduced a nonlinear 4D-system of ordinary differential equations describing COVID-19. Atangana [10] formulated a numerical design using the Newton polynomial. Other strategies can be located in efforts by Memon et al. [11]. Newly, numerous mathematical simulations have been indicated to realize the coronavirus infection. Supreme of these representations are based on classical integer-order derivative or classical fractional differential operators, which cannot get the vanishing memory and boundary performance found in numerous biological phenomena. Consequently, we investigate the coronavirus disease in this study by discovering the dynamics of COVID-19 infection utilizing the fractional Caputo derivative.
The terminal coronavirus continues to blow out across the globe, and mathematical models can be utilized to display suspected, recovered, and deceased coronavirus patients, as well as how many persons have been tested or even vaccinated. Consequently, mathematical and statistical solutions of the infected human beings overall can decrease the risk of future COVID-19 spread. In this study, we aim to generalize the Wilson–Cowan system (WCS) utilizing the concept of fractional calculus to study the growth of COVID-19 population. This investigation includes a dynamic term, which is the exponential law to discover and realize the graph of the growth. The solvability of the system is indicated by using the optimal point theorem of simulation function. Other behaviors are indicated such as the approximated solvability using the fractional Tutte polynomials.
2 Preparations
This section deals with some concepts and the properties of these concepts.
2.1 ABC-definition
In recent decades, numerous physical issues have been exposed using the fractional calculus. The essential explanations for employing fractional calculus are that various measures, structures, and inequities display capability to remember the past or nonlocal possessions. The basic outlook and appearances of fractional calculus and fractional differential equations are recognized in various reviews. Most researches focus on the derivatives, which include kernels. For instance, the main difference between the Caputo operator, the Caputo–Fabrizio operator [12], and others is that the Caputo operator is communicated by giving a power law, the Caputo–Fabrizio operator is adapted by utilizing an exponential growth act. The Atangana–Baleanu operator is presented by signifying the extended Mittag-Leffler function [13].
Definition 2.1
Let \(\Lambda ^{\mu }\), \(\mu \in (0,1)\) be the Atangana–Baleanu operator of order μ of a function χ fulfilling
where \(B(\mu )\) indicates a normalization function, Ξ represents the Mittag-Leffler function. Corresponding to \(\Lambda ^{\mu }\), the ABC integral is realized by
Example 2.1
Consider the function \(\chi (t)=t^{m}\), then the ABC integral becomes
In our study, since we focus on the approximated solutions, we assume that \(B(\mu ) \rightarrow 1\) for all \(\mu \in (0,1)\). Applications of this calculus in COVID-19 can be located in [14–16].
2.2 Approximate point theorem
We deal with the resulting notion of cyclic ∁-condensing operator. Let ð be a measure of noncompactness on a Banach space \(\mathbb{X}\) and A, B be nonempty and convex subsets of \(\mathbb{X}\) (see [17]).
Definition 2.2
A function \(f: \mathbb{R}_{+} \times \mathbb{R}_{+} \rightarrow \mathbb{R}\) is called simulation if and only if \(f(0,0)=0\), \(f(x_{1},x_{2})< x_{2}-x_{1}\), where \(x_{2},x_{1}>0\) and \(\lim_{i \rightarrow \infty } \sup f(x_{i},y_{i})<0\) for \(x_{i}< y_{i}\) and \(\lim_{i \rightarrow \infty } x_{i}=\lim_{i \rightarrow \infty } y_{i}=0\).
Definition 2.3
Let \(Y: A\cup B \rightarrow A\cup B\) be an operator. It is f-cyclic condensing (CC) if, for every nonempty, bounded, convex, and closed subset \((A_{1},B_{1})\),
Lemma 2.2
A relatively nonexpansive cyclic f-condensing mapping \(Y: A\cup B \rightarrow A\cup B\) recognizes a best proximity point.
3 Results
We let \(\mathbb{N} (t) \) be the accumulation number of infected people, which represents the sum of the number of the standard infected persons \(\chi (t)\) and that of the asymptomatic transmission ones \(\Upsilon (t)\): \(\mathbb{N} (t) =\chi (t) + \Upsilon (t)\). Take into account that \(\chi (t)\) includes people who have previously been diseased. Therefore, there are rate functions joining χ and ϒ. The following integro-differential system indicates the generalization of WCS. We suggest the generalization by using the ABC formula of fractional calculus as follows:
where the variables are defined in different intervals: \(\Pi =[\tau _{1}-\tau _{2},\tau _{1}+\tau _{2}]\), \(\Pi _{\chi }= [\chi _{1}- \epsilon ,\chi _{1}+ \epsilon ]\), \(\Pi _{\Upsilon }= [\Upsilon _{1}-\epsilon ,\Upsilon _{1}+ \epsilon ]\), and \(\Pi _{\epsilon }=[\tau _{1}-\epsilon ,\tau _{1}+\epsilon ]\).
To study the solvability of system (1), we formulate the following assumptions:
-
(A1)
All the functions are continuous in \(\mathbb{R}\) such that \(\phi _{1}: \Pi \times \Pi \times \Pi _{\chi }\rightarrow \mathbb{R}\), \(\phi _{2}: \Pi \times \Pi \times \Pi _{\Upsilon }\rightarrow \mathbb{R}\), \(\Psi _{1}: \Pi _{\epsilon }\times \Pi _{\chi }\times \Pi _{\chi }\times \Pi _{\chi }\rightarrow \mathbb{R}\), \(\Psi _{2}: \Pi _{\epsilon }\times \Pi _{\Upsilon }\times \Pi _{\Upsilon }\times \Pi _{\Upsilon }\rightarrow \mathbb{R}\) and χ, ϒ are inside the nonempty, bounded, closed, and convex sets \(\intercal _{1}\subset C(\Pi _{\epsilon },\mathbb{R})\) and \(\intercal _{2} \subset C(\Pi _{\epsilon },\mathbb{R})\) respectively.
-
(A2)
For a sup.norm, we suppose that \(\|\chi _{1}-\Upsilon _{1}\|\leq \epsilon \|\chi -\Upsilon \|\), \(0< \epsilon \leq 1\), so that \(\operatorname{dis} (\intercal _{1},\intercal _{2})=\|\chi _{1}-\Upsilon _{1}\|\). In addition, for all \(\chi \in \intercal _{1}\) and \(\Upsilon \in \intercal _{2}\), we suppose that there occurs a positive constant \(\rho >0\) fulfilling
$$ \Vert \Psi _{1}-\Psi _{2} \Vert \leq \rho \bigl( \Vert \chi -\Upsilon \Vert - \Vert \chi _{1}-\Upsilon _{1} \Vert \bigr). $$ -
(A3)
For any \(\Pi _{\chi }\), \(\Pi _{\Upsilon }\), there exists a positive function
 which is upper semi-continuous and achieves
which is upper semi-continuous and achieves  and
and

Here, we introduce our theorem for the solvability of system (1). We define an operator \(\mathbb{Q}: \intercal _{1} \cup \intercal _{2} \rightarrow C(\Pi _{\epsilon },\mathbb{R})\) as follows:
Theorem 3.1
Consider system (1) satisfying hypotheses (A1)–(A3). Then it has an optimal solution in \(C(\Pi _{\epsilon },\mathbb{R})\), whenever
Proof
Consider the operator \(\mathbb{Q}\) and \(B(\mu )\rightarrow 1\). We aim to show that \(\mathbb{O}\) is a cyclic operator. Let \(\chi \in \intercal _{1}\), then we get
where \(S_{1}:=\sup (\Psi _{1})=\|\Psi _{1}\|\). By letting \((_{1}\epsilon _{\mu })< \frac{\bar{\epsilon }_{\mu }}{\max \{S_{1},S_{2}\}}\), where \(\bar{\epsilon }_{\mu }:=\max \{ _{1}\epsilon _{\mu }, _{2}\epsilon _{\mu }\}\) and \(S_{2}:=\sup (\Psi _{2})\), we have
Thus, \(\mathbb{Q}\chi \in \intercal _{2}\). In the same manner, we conform that, for \(\Upsilon \in \intercal _{2}\), this indicates that
and hence \(\mathbb{Q}y \in \intercal _{1} \). We conclude that \(\mathbb{Q}\) is cyclic. The above conclusion shows that the set \(\mathbb{Q}(\intercal _{1})\) is bounded in ⊺2, and the set \(\mathbb{Q}(\intercal _{2})\) is bounded in ⊺1.
Recall that \(\phi \in \intercal _{1} \cup \intercal _{2}\) indicates an optimum outcome of system (1) if and only if \(\operatorname{dist} (\intercal _{1} \cup \intercal _{2})=\|\phi -\mathbb{Q}\phi \|\). Therefore, we have to prove this fact. Next, we aim to prove that \(\mathbb{Q}(\intercal _{1} )\) is equicontinuous in ⊺2. For ς and \(\varsigma '\), we have
which implies that \(\mathbb{Q}(\intercal _{1}) \) is equicontinuous in ⊺2. In a similar manner, we confirm that \(\mathbb{Q}(\intercal _{2}) \) is equicontinuous in ⊺1. As a consequence and via the Arzela–Ascoli theorem, we point that the pair \((\intercal _{1},\intercal _{2})\) is relatively compact. Now, we have to show that \(\mathbb{Q}\) is relatively nonexpansive.
For \((\chi ,\Upsilon ) \in (\intercal _{1},\intercal _{2})\), we inform that
But ϵ is an arbitrary constant, thus when \(\epsilon \rightarrow 0\), we have the inequality
This indicates that \(\mathbb{Q}\) is relatively nonexpansive.
We proceed to show that \(\mathbb{Q}\) is f-condensing. Assume that \((\Pi _{\chi },\Pi _{\Upsilon })\subseteq (\intercal _{1},\intercal _{2})\) is a nonempty, bounded, closed, and convex set such that

Thus, we obtain

By putting  , then we arrive at
, then we arrive at

Hence, the necessary requirements of Lemma 2.2 are achieved. Thus, the operator \(\mathbb{Q}\) has the best proximity point and thus system (1) has an optimal solution.
This completes the proof. □
3.1 Numerical structures
In this subsection, we introduce some numerical systems pointing to utilize Theorem 3.1. The chief assumption in Theorem 3.1 is \(\rho < \frac{\Gamma (\mu )}{\Gamma (\mu )+(1-\mu )+\bar{\epsilon }_{\mu }}\). This inequality is very informal to fulfill likening with other existence theorems attaining (A1–A3). Theorem 3.1 designates that the system attractive formula (1) admits an optimal solution. This kind of result is very significant in dynamic and control systems. By this result, one can investigate the stability, oscillatory solution, and other performances of the resolution.
Example 3.2
By using Mathematica 11.2, the solution is realized by the integral
where c is a constant and W represents the product log function. As an application of Theorem 3.1, we assume that \((\chi _{0},\Upsilon _{0})=(1,1)\) and \(\rho = (\upsilon _{2}\upsilon _{3}-\upsilon _{1}\upsilon _{4})\), where
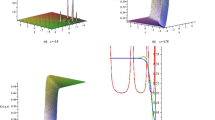
For instance, \((\upsilon _{1},\upsilon _{2},\upsilon _{3},\upsilon _{4})=(2,1,0.4,0.1)\), we attain \(\rho =0.2<0.341\); thus, by Theorem 3.1, system (3) admits an optimal solution converging to a limit cycle. In another case, suppose that \((\upsilon _{1},\upsilon _{2},\upsilon _{3},\upsilon _{4})=(1,1,0.9,0.8)\), then \(\rho =0.1<0.341\). This implies that system (3) admits optimal solution converging to a limit cycle. Similarly, for \((\upsilon _{1},\upsilon _{2},\upsilon _{3},\upsilon _{4})=(1,1,1,0.8) \Rightarrow \rho = 0.2<0.341\) and \((\upsilon _{1},\upsilon _{2},\upsilon _{3},\upsilon _{4})=(1,0.9,1,0.8) \Rightarrow \rho = 0.1<0.341\). Figure 1 represents various cases considering the value of ρ.
Results of (3) with various values of ρ. From the upper left, the solution is for \((\upsilon _{1},\upsilon _{2},\upsilon _{3},\upsilon _{4})=(2,1,0.4,0.1)\), while the lower left is the optimal outcome for \((1,1,0.9,0.8) \). The upper and lower right graphs represent the solutions for \((1,1,1,0.8) \) and \((1,0.9,1,0.8) \) respectively. We indicate that the cyclic result for these values is based on the fact that \(\mathbb{Q}\) is cyclic
Example 3.3
Consider the following system:
where the value of ρ achieves
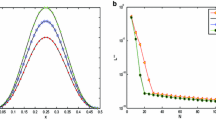
For instance, when \(\rho =0.4\), we have an optimal solution with the initial condition \((\chi _{0},\Upsilon _{0})=(0,0)\). Furthermore, it is unstable cyclic because it indicates a portrait unstable limit cycle (see Fig. 2, the upper graphs). When \(\rho =0.1\), the system admits an optimal solution with a portrait unstable limit cycle (see Fig. 2, the lower graphs).
Solutions of (4) for different cases, depending on the value of ρ. We recognize that the cyclic solution for these cases is based on the fact that \(\mathbb{Q}\) is cyclic
Remark 3.1
The upper value of ρ plays an important role in describing the behavior of the optimal solution. It represents that when the upper value of ρ is equal to 0.33, then we have a stable solution (see Example 3.2). If the value is greater than 0.33, we have an unstable optimal solution (see Example 3.3). We shall take into account this fact when we establish the connections of Tutte polynomials in the next section.
3.2 Approximated solution
In this section, we aim to use a type of polynomial to approximate the solution of (1). In this place, we suggest to use the Tutte polynomial because the formality of this polynomial involves two variables as follows (see [18]):
By using the construction of Example 2.1, we have the fractional Tutte polynomial as follows:
To determine the upper bound (approximated value) of \(\omega (i,j)\), based on Theorem 2.2, we shall consider that these weights satisfy the upper bound of ρ, which is given by the formula
Note that \(\lim_{\mu \rightarrow 1} \omega (\varsigma ,\tau )=0.33\) providing that \(\varsigma -\tau =1\). This value is approximated with the upper bound of ρ in Example 3.2. By suggesting the solution of system (3) in terms of fractional Tutte polynomials, we have
We suppose that χ and ϒ have the same gathering of roots as the original polynomials. That is, these polynomials can be recognized in a Grobner basis (GB). For linear functions in any number of variables, GB is analogous to Gaussian elimination. For example, if \((\chi (\varsigma ),\Upsilon (\varsigma ))= (\varsigma ,\tau )\), then \(\operatorname{GB}(\varsigma ,\tau )=\{\varsigma ,\tau \}\) (see Fig. 3). For nonlinear cases, we have the following results.
GB for the linear case. From the left: the graph represents 3D solution, contour plot, and integral curve. Similarly, for the case \((\tau ,\varsigma )\) for all real coefficients. The second row is GB of fractional order \(\mu =0.5\), which indicates the set \(\{\varsigma ,\tau ,\sqrt{\tau +\varsigma }, \sqrt{\varsigma }+\sqrt{ \tau }\}\)
Example 3.4
\(\operatorname{GB}(\chi (\varsigma ),\Upsilon (\varsigma ))=\operatorname{GB} (\tau ^{2}-\varsigma ^{2}, \tau *\varsigma )=\{ \tau ^{3},\tau \varsigma ,\varsigma ^{2}-\tau ^{2} \}\) with \((0,0)\) root (see Fig. 4).
Example 3.5
\(\operatorname{GB}(\chi (\varsigma ),\Upsilon (\varsigma ))=\operatorname{GB} (\tau ^{2}-\varsigma ^{2}, \tau *\varsigma -0.33)=\{ \tau ^{4}-0.1089,\varsigma -3.03\tau ^{3}\}\) with the real root \((\frac{\sqrt{33}}{10},\frac{\sqrt{33}}{10})\) (see Fig. 5).
Example 3.6
\(\operatorname{GB}(\chi (\varsigma ),\Upsilon (\varsigma ))=\operatorname{GB} (\varsigma ^{3}-\tau ^{2}, \varsigma -\tau )=\{ \tau ^{3}-\tau ^{2}, \varsigma -\tau \}\) with two real roots \((0,0)\) and \((1,1)\) (see Fig. 6).
Example 3.7
\(\operatorname{GB}(\chi (\varsigma ),\Upsilon (\varsigma ))=\operatorname{GB} (\varsigma ^{3}+\tau ^{2}, \varsigma *\tau )=\{ \varsigma ^{3}, \varsigma \tau , \varsigma ^{2}+ \tau ^{2}\}\) with one real root \((0,0)\) (see Fig. 7).
GB for the nonlinear case in Example 3.7
3.3 Application
In this subsection, we shall utilize live data regarding COVID-19, which were recorded in May. Figures 8 and 9 indicate live data which were recognized in May for Brazil and USA. By using the approximated solution, we see that the data converge to the result of different BG values where the value of τ indicates the starting situation. Experimentally, we indicate that the good result appears, when the value of fractional order \(\mu \rightarrow 1\) and the interval of convergence solution is \(\mu \in (0.8,0.99] \).
4 Conclusion
By using the fractional calculus, type ABC, we have generalized WCS. We have got two kinds of solutions, the first one is the optimal solution (see Theorem 3.1) using the concept of simulation function and the second is approximated solution using the GB set of polynomials of two variables \((\tau ,\varsigma )\). The optimal solution brings the stability, oscillation, and periodicity. The second solution is validated for discrete data. In this investigation, we generalized the most popular graph polynomials called the Tutte polynomial and a variety of carefully related graph polynomials such as the harmonic, movement, reliability, and shelling polynomials. We also used the Tutte polynomial to demonstrate how graph polynomials may be both dedicated and generalized, and how they can convert information relevant to medical applications. We concluded with a brief conversation of computational complexity deliberations. Different studies are presented using fractional calculus together with statistics and polynomials categories, which can be located in [19–25].
Availability of data and materials
Data sharing not applicable to this article as no data-sets were generated or analyzed during the current study.
References
Wilson, H.R., Cowan, J.D.: A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik 13(2), 55–80 (1973)
Wilson, H.R., Blake, R., Lee, S.-H.: Dynamics of travelling waves in visual perception. Nature 412(6850), 907–910 (2001)
World, Organization, H.: Coronavirus disease (COVID-19) outbreak. https://www.who.int/emergencies/diseases/novel-coronavirus-2019
World Health Organization: Coronavirus disease (COVID-19) report. https://www.who.int/docs/default-source/coronaviruse/who-china-joint-mission-on-covid-19-final-report.pdf
Lanteri, D., Carco, D., Castorina, P.: How macroscopic laws describe complex dynamics: asymptomatic population and COVID-19 spreading (2020) arXiv:2003.12457
Atangana, A.: Modelling the spread of COVID-19 with new fractal-fractional operators: can the lockdown save mankind before vaccination? Chaos Solitons Fractals 136, 109860 (2020)
Atangana, A., Araz, S.: Modeling and forecasting the spread of COVID-19 with stochastic and deterministic approaches: Africa and Europe. Adv. Differ. Equ. 2021(1), 1 (2021)
Atangana, A., Araz, S.I.: Mathematical model of COVID-19 spread in Turkey and South Africa: theory, methods, and applications. Adv. Differ. Equ. 2020(1), 1 (2020)
Musa, S.S., Qureshi, S., Zhao, S., Yusuf, A., Mustapha, U.T., He, D.: Mathematical modeling of COVID-19 epidemic with effect of awareness programs. Infect. Dis. Model. 6, 448–460 (2021)
Atangana, A.: A novel Covid-19 model with fractional differential operators with singular and non-singular kernels: analysis and numerical scheme based on Newton polynomial. Alex. Eng. J. 60(4), 3781–3806 (2021)
Memon, Z., Qureshi, S., Rasool Memon, B.: Assessing the role of quarantine and isolation as control strategies for COVID-19 outbreak: a case study. Chaos Solitons Fractals 144, 110655 (2021)
Caputo, M., Fabrizio, M.: A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 1(2), 1–13 (2015)
Atangana, A., Baleanu, D.: New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model (2016) arXiv:1602.03408
Ahmad, Z., Arif, M., Ali, F., Khan, I., Nisar, K.S.: A report on COVID-19 epidemic in Pakistan using SEIR fractional model. Sci. Rep. 10(1), 1–14 (2020)
Khan, A., Alshehri, H.M., Abdeljawad, T., Al-Mdallal, Q.M., Khan, H.: Stability analysis of fractional nabla difference COVID-19 model. Results Phys. 22, 103888 (2021)
Abdo, M.S., Shah, K., Wahash, H.A., Panchal, S.K.: On a comprehensive model of the novel coronavirus (COVID-19) under Mittag-Leffler derivative. Chaos Solitons Fractals 135, 109867 (2020)
Patle, P.R., Patel, D.K., Arab, R.: Darbo type best proximity point results via simulation function with application. Afr. Math. 31, 833–845 (2020)
Tutte, W.T.: A contribution to the theory of chromatic polynomials. Can. J. Math. 6, 80–91 (1954)
Hadid, S.B., Ibrahim, R.W., Altulea, D., Momani, S.: Solvability and stability of a fractional dynamical system of the growth of COVID-19 with approximate solution by fractional Chebyshev polynomials. Adv. Differ. Equ. 2020(1), 1 (2020)
Hasan, A.M., Al-Jawad, M.M., Jalab, H.A., Shaiba, H., Ibrahim, R.W., AL-Shamasneh, A.R.: Classification of COVID-19 coronavirus, pneumonia and healthy lungs in CT scans using q-deformed entropy and deep learning features. Entropy 22(5), 517 (2020)
Ibrahim, R.W., Altulea, D., Elobaid, R.M.: Dynamical system of the growth of COVID-19 with controller. Adv. Differ. Equ. 2021(1), 1 (2021)
Momani, S., Ibrahim, R.W., Hadid, S.B.: Susceptible-infected-susceptible epidemic discrete dynamic system based on Tsallis entropy. Entropy 22(7), 769 (2020)
Irfan, O., Muttalib, F., Tang, K., Jiang, L., Lassi, Z.S., Bhutta, Z.: Clinical characteristics, treatment and outcomes of paediatric COVID-19: a systematic review and meta-analysis. Arch. Dis. Child. 106(5), 440–448 (2021)
Alderremy, A.A., Gómez-Aguilar, J.F., Aly, S., Saad, K.M.: A fuzzy fractional model of coronavirus (COVID-19) and its study with Legendre spectral method. Results Phys. 21, 103773 (2021)
Yousaf, M., Zahir, S., Riaz, M., Hussain, S.M., Shah, K.: Statistical analysis of forecasting COVID-19 for upcoming month in Pakistan. Chaos Solitons Fractals 138, 109926 (2020)
Acknowledgements
The authors would like to express their full thanks to the respected editor and reviewers for the deep advise, which improved our paper.
Funding
This research received no external funding.
Author information
Authors and Affiliations
Contributions
All authors contributed equally and significantly to writing this article. All authors read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hadid, S.B., Ibrahim, R.W. Fractional dynamic system simulating the growth of microbe. Adv Differ Equ 2021, 351 (2021). https://doi.org/10.1186/s13662-021-03498-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03498-3



 which is upper semi-continuous and achieves
which is upper semi-continuous and achieves  and
and









