Abstract
We present a collocation approach based on redefined cubic B-spline (RCBS) functions and finite difference formulation to study the approximate solution of time fractional Allen–Cahn equation (ACE). We discretize the time fractional derivative of order \(\alpha\in(0,1]\) by using finite forward difference formula and bring RCBS functions into action for spatial discretization. We find that the numerical scheme is of order \(O(h^{2}+\Delta t^{2-\alpha})\) and unconditionally stable. We test the computational efficiency of the proposed method through some numerical examples subject to homogeneous/nonhomogeneous boundary constraints. The simulation results show a superior agreement with the exact solution as compared to those found in the literature.
Similar content being viewed by others
1 Introduction
Nonlinear evolution equations have numerous applications in various fields of engineering, physics, chemistry, and biology such as chemical reactions, gas and fluid mechanics, elasticity, optical fiber, relativity, solid state and plasma physics, ecology and biomechanics, and so on [1]. Analytical and numerical study of traveling wave equations has always remained an interesting topic for the researchers. The fractional first integral method [2], the fractional exp-function approach [3], the fractional \(\acute {G}/G\)-expansion scheme [4], the fractional variable method [5], the fractional modified trial equation algorithm [6], the fractional subequation method [7], the fractional simplest equation formulation [8], and the Tanh method using fractional complex transform [9] are some efficient and famous methods for solving fractional-order nonlinear problems.
So far, intensive efforts have been made to study the time fractional phase-field models, as these models catch great attention in the field of phase transitions [10]. Mostly two very important phase-field partial differential equation (PDE) models, the Allen–Cahn and Cahn–Hilliard models, have been studied rigorously [11]. The Allen–Cahn model is used to describe the motion of phase boundaries in crystalline solids [12]. It also appears in some other applications such as mixture of two incompressible fluids, vesicle membranes, and nucleation of solids [13–15].
In this paper, we consider the following time fractional ACE, which arises in mathematical modeling of phase separation in alloys of iron [1]:
subject to the initial conditions
and boundary conditions
where \(\phi_{0}(z)\) and \(\psi_{i}(z)\) are supposed to be smooth functions with continuous first-order derivatives. There are many interpretations of fractional-order derivatives [16–19]. However, we have considered the fractional derivative in Caputo sense as [20]
where Γ is the usual gamma function. A lot of work on analytical solutions of time fractional ACE is available in the literature. Esen et al. [21] employed homotopy analysis method (HAM) to find the exact solution of time fractional ACE. The exact solution of space-time fractional ACE was discussed in [22] by means of a fractional subdiffusion method. The authors in [23] studied the coarsening of domains in a subdiffusive ACE in the context of the Seki–Lindenberg subdiffusion–reaction model. Yasar and Giresunlu [24] examined the exact solution of nonlinear space-time fractional ACE using \((\frac{\acute{G}}{G}.\frac{1}{G})\)-expansion algorithm. Guner et al. [25] solved the time fractional nonlinear ACE by means of the first integral, the exp-function and \((\frac{\acute {G}}{G})\)-expansion methods. Zhai et al. [26] applied a robust explicit operator splitting spectral approach to solve the nonlocal fractional Allen–Cahn model. The existence and uniqueness of weak solutions for the fractional Allen–Cahn, Cahn–Hilliard, and porous medium equations have been discussed by Akagi [27].
Tariq and Akram [1] proposed an analytical approach to determine the exact solutions for time fractional ACE. The authors applied the fractional complex transform method to reduce the equation into nonlinear ordinary differential equation (ODE). To explore numerical solution of space fractional ACEs, Hou et al. [28] employed the finite difference and Crank–Nicolson schemes for temporal and spatial discretization, respectively. Li et al. [29] explored the numerical solution of space-time fractional Allen–Cahn phase-field equation arising in the study of fluid mixture having two immiscible fluid phases. Some new exact solutions for time fractional ACE were presented by Hosseini et al. [30] using a new Kudryashov method in perspective of the conformable fractional derivative.
Most recently, Sakar et al. [31] proposed a numerical scheme based on the iterative reproducing kernel method (IRKM) to investigate the approximate solution of time fractional ACE. Liu et al. [32] developed a numerical scheme based on finite difference formulation and the Fourier spectral method to solve time fractional ACE in one and two space dimensions. Smooth and nonsmooth solutions for nonlinear space fractional ACE were studied by Yin et al. [33] using a fast algorithm based on time two-mesh finite difference method. Inc et al. [34] reduced the time fractional ACE and time fractional Klein–Gordon equations into the corresponding nonlinear fractional ODEs and employed an explicit power series method to solve these fractional ODEs. Khalid et al. [35] proposed a numerical approach based on cubic modified extended basis spline functions for time fractional diffusion wave equations. The authors in [36] employed nonpolynomial quintic spline functions for numerical investigation of fourth-order fractional boundary value problems involving product terms.
In this paper, we present a redefined cubic B-spline (RCBS) algorithm for numerical investigation of time fractional ACEs. The Caputo time fractional derivative has been discretized by finite difference formula, whereas spatial derivatives are discretized by RCBS functions. This approach is novel for numerical solution of fractional-order ACEs, and to the best of our knowledge, spline solution of time fractional ACE has never been studied yet. Moreover, this scheme is equally effective for homogeneous and nonhomogeneous boundary conditions.
This paper is organized as follows. Section 2 evolves a brief description of temporal discretization, cubic B-spline functions, and spatial discretization. In Sect. 3, we discuss the stability of the proposed algorithm. The theoretical convergence analysis is presented in Sect. 4. The discussion on numerical results of three test problems has been reported in Sect. 5.
2 Description of the method
2.1 Temporal discretization
Let the time interval \([0,T]\) be divided into M subintervals of equal length \(\Delta t=\frac{T}{M}\) such as \(0=t_{0}< t_{1}<\cdots<t_{M}=T\), where \(t_{n}=n \Delta t\), \(n=0,1,\dots,M\). The Caputo definition given in Eq. (4) for time fractional derivative can be rewritten as
Using forward difference formulation, Eq. (5) can be modified as
Hence
where \(\delta_{k} = (k+1)^{1-\alpha}-(k)^{1-\alpha}\), \(\rho= t_{n+1}-\tau\), and the truncation error \(\eta_{\Delta t}^{n+1}\) is bounded,
where ϖ is a finite constant.
Lemma 2.1
The coefficients\(\delta_{r} \)possess following characteristics [20]:
\(\delta_{0}=1 \), \(\delta_{k}>0 \), \(k=1,\dots,n \);
\(\delta_{0}>\delta_{1}>\delta_{2}>\cdots> \delta_{k} \rightarrow0 \)as\(k \rightarrow\infty\)
\(\sum_{k=0}^{n}(\delta_{k}-\delta_{k+1})+\delta_{n+1}=(1-\delta _{1})+\sum_{k=1}^{n-1} (\delta_{k}-\delta_{k+1})+\delta_{n}=1\).
Substituting Eq. (6) into Eq. (1), we get
where F is a nonlinear term such as \(F (u(z,t) )=u^{3}(z,t)\). We can write the last equation in the following form:
where \(r= \frac{1}{\varGamma(2-\alpha) (\Delta t)^{\alpha}}\), \(u(z,t_{n+1})=u^{n+1}\), \(n=0,1,\dots,M \).
2.2 Cubic B-spline functions
Consider the space interval \([a,b]\) divided into N piecewise uniform spacing subintervals of length \(h= z_{j}-z_{j-1}=\frac{b-a}{N}\), \(j=1,\dots,N\), such that \(a=z_{0}< z_{1}<\cdots<z_{N}=b\). In typical cubic B-spline collocation method, the approximation \(U^{*}(z,t)\) to the exact solution \(u(z,t)\) is
where \(\gamma_{j}(t)\) are time-dependent unknowns to be computed. The cubic B-spline functions are twice differentiable at the nodal points \(z_{j}\) over the domain \([a,b]\) and preserve identical properties like nonnegativity, local support, convex, full property, symmetry, partition of unity, and geometric invariability. The blending function \(B_{j}(z)\) of cubic B-spline can be represented in the following form [37]:
where \(B_{-1},B_{0}, \dots,B_{N+1}\) can serve as spline basis over the domain \([a,b]\). The values of \(B_{j}(z)\), \(B'_{j}(z)\), and \(B''_{j}(z)\) are given in Table 1 [38].
The approximate solution \((U^{*})_{j}^{n}=U^{*}(z_{j},t^{n})\) with its first- and second-order derivatives at the nth time level in terms of \(\gamma_{j}\) can be written as
2.3 Redefined cubic B-spline functions
Usually, in collocation techniques, the Dirichlet type end conditions are imposed where the basis of spline functions vanish, but the CBS functions \(B_{-1},B_{0}, \dots,B_{N+1}\) do not vanish at the boundaries. So we redefine these bases so that they vanish at the boundaries when Dirichlet-type end conditions are prescribed [38, 39].
The spline solution \(U(z,t)\) for the exact solution \(u(z,t)\) is obtained by eliminating \(\gamma_{-1}^{n}\) and \(\gamma_{N+1}^{n}\) from Eq. (10) as follows:
where the weight function \(\widetilde{W}(z,t)\) and RCBS \(\widetilde {B}_{j}(z)\) functions are given by
Using Eq. (13) in Eq. (9), we obtain
Let \(({\widetilde{W}{^{*}}})^{n+1}\) be the resultant term obtained from the weight functions. Then the last equation becomes
Letting \(g^{n+1}=f^{n+1}-F^{n}-({\widetilde{W}{^{*}}})^{n+1}\) and using the values given in Table 1 with Eqs. (14) and (15) in Eq. (16), we form a recurrence relation after some simplifications:
where \(\rho_{0}=\frac{6}{h^{2}}\), \(\rho_{1}= (\frac{r-1}{6} -\frac {1}{h^{2}} )\), and \(\rho_{2}= 2 (\frac{r-1}{3}+\frac{1}{h^{2}} )\). The system of equations (17) in matrix form is given by
where
Using the initial conditions given in Eq. (2), we obtain the initial vector \(\gamma^{0}=[\gamma_{0}^{0},\gamma_{1}^{0}, \dots, \gamma _{N}^{0}]^{T}\) required to initiate the iteration process. We apply the initial conditions as follows:
This gives \(N+1\) linear equations and can be written as
where
3 Stability analysis
A numerical algorithm is considered to be stable if the errors do not propagate during the execution [40]. Here we employ the Fourier method to carry out the stability analysis of the proposed scheme. Let \(\varPhi^{n}\) represent the growth factor in Fourier mode, and let \(\tilde{\varPhi}^{n}\) be its approximate value. The error \(\lambda _{i}^{n}\) at the nth time level is given by
where \(\lambda^{n}=[\lambda_{1}^{n}, \lambda_{2}^{n}, \dots, \lambda _{N-1}^{n}]^{T}\).
For simplicity, we study the stability in Eq. (17) for linear case (\(g=0\)) only. Using Eqs. (21) and (17), we get the round-off error in the form
The initial condition is satisfied by the error equation
and similarly the boundary conditions become
Define a grid function in the Fourier form:
Now, in the Fourier series form, \(\lambda^{n}(z)\) can be expressed as
where
Applying the norm, we obtain
Hence
Let \(\lambda_{j}^{n}=\epsilon_{n} e^{i \nu j h}\) be the solution in the Fourier series form, where \(i=\sqrt{-1}\) and \(\nu={\frac{2\pi m }{b-a}}\).
Using the expression \(\lambda_{j}^{n}=\epsilon_{n} e^{i \nu j h}\) in Eq. (22) and then dividing by \(e^{i \nu j h}\), we obtain
Using the relation \(e^{i \nu h }+e^{-i \nu h } = 2 \cos(\nu h)\), we can collect like terms in the following way:
where \(b^{*}=1+\frac{12 \sin^{2}(\nu h /2)-h^{2}(2+\cos(\nu h))}{ah^{2}(2+\cos (\nu h))}\), and we can see that \(b^{*}\geq1\).
Theorem 1
The fully implicit scheme given in (17) is unconditionally stable if\(|\epsilon_{n}|\leq|\epsilon_{0}|\), \(n=0,1,\dots,T \times M \), where\(\epsilon_{n}\)is the solution of (30).
Proof
First of all, we have to prove by induction that \(|\epsilon_{n}|\leq |\epsilon_{0}|\) for \(n=0,\dots,T \times M \).
For \(n=0\), Eq. (30) takes the form
Let us assume that the result \(|\epsilon_{n}|\leq |\epsilon_{0}|\) is true for \(n=1,2,\dots T \times M-1\).
Now expression (30) can be written as
Hence
Now, using Eqs. (28) and (31), we get
This proves that the implicit scheme (17) is unconditionally stable. □
4 Convergence analysis
We follow the technique used in [41] to investigate the uniform convergence of the proposed algorithm. Firstly, we state the following theorem [42, 43].
Theorem 2
Suppose that the exact solution\(u(z,t)\in C^{4}[a,b]\), \(f \in C^{2}[a,b]\), \(\Delta=\{a=z_{0},z_{1}, \ldots, z_{N}=b\}\)is an equidistant partition, each of lengthh, over the interval\([a,b]\)such that\(z_{j}=jh\), \(j= 1,\dots,N\). Let\(\tilde{U}(z,t)\)be the unique spline approximation to the given problem at the spatial grid points\(z_{j} \in \Delta\), \(j= 0,\dots,N\), then for all\(t\geq0\), there exist\(\mu_{j}\), independent ofh, such that
Lemma 4.1
The B-spline set\(\{B_{0},B_{1}, \ldots, B_{N}\}\)presented in (10) satisfies the inequality
Proof
By the triangle inequality we can write
For grid points \(z_{j}\), we get
Further, for a point \(z \in[z_{j},z_{j+1}]\), we have
where
Hence
□
Theorem 3
LetUbe the numerical approximation to the analytical exact solution ufor Eqs. (1)–(3). If\(f\in C^{2}[0,1]\), then we have
where\(\varOmega>0\)is a constant independent fromh, andhis sufficiently small.
Proof
Let u be the exact solution, and let \(\tilde{U}=\sum_{j=0}^{N} c_{j}(t) B_{j}\) be the spline approximation for U.
Let \(Lu(z_{j},t)=LU(z_{j},t)=g(z_{j},t)\), \(j=0,\dots,N \), be the accumulation conditions. Then
At the nth time stage, the present BVP can be written in the form of the difference equation \(L(\tilde{U}(z_{j},t)-U(z_{j},t))\):
Also, the boundary constraints are
where
and
It is evident from (32) that
We define \(\sigma^{n}=\max\{|\sigma_{j}^{n}|;0 \leq j \leq N \}\), \(\tilde {e}_{j}^{n}=|\xi_{j}^{n}|\), and \(\tilde{e}^{n}=\max\{|e _{j}^{n}|;0 \leq j \leq N \} \).
For \(n=0\), Eq. (36) gives
where \(j=0,\dots,N\), and by the initial condition \(e^{0}=0\) this implies
Taking the absolute values of \(\sigma_{j}^{n}\) and \(\xi_{j}^{n}\) with sufficiently small h, we have
Using the boundary conditions, we conclude that
where \(\mu_{1}\) does not depend on h.
Using induction procedure on n, suppose that \(\tilde{e}_{j}^{k}\leq\mu_{k} h^{2}\) for \(k=1,\dots,n\).
Let \(\mu=\max\{\mu_{k}: 0\leq k \leq n \}\). Then Eq. (36) becomes
Again, taking the absolute values of \(\sigma_{j}^{n}\) and \(\xi_{j}^{n}\) with very small h, we get
Also, from the boundary conditions we have
Thus, for all n, we have
Now
Utilizing Lemma 4.1, we arrive at
Using the triangle inequality, the previous expression yields
Using inequalities (32) and (41) in (42), we obtain
where \(\varOmega=\mu_{0} h^{2}+ \frac{5}{3} \mu\). □
The proved theorem and relation (7) yield that the presented numerical scheme is convergent. Hence
where ϖ and Ω are real constants, and \(\alpha\in (0,1]\). This implies that the experimental order of convergence (EOC) of the proposed method is \(O(h^{2}+\Delta t^{2-\alpha})\).
5 Numerical experiments and discussion
In this section, we present three numerical experiments to check the efficiency of the proposed scheme for time fractional ACE. We test the computational results through error norms \(L_{2}\) and \(L_{\infty}\) and the experimental order of convergence (EOC) as
All computations are done by using MATHEMATICA 9.0 software.
Problem 1
Consider the time fractional ACE [31]:
where
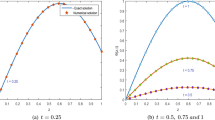
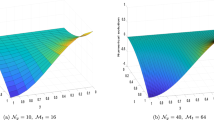
The initial and boundary constraints can be extracted from the exact solution \((z^{2}-z) t^{1+\alpha}\). A comparison of the maximum absolute error with IRKM [31] is presented in Tables 2, 3, 4, 5. The computational results are reported for \(\alpha=0.7, 0.9\), \(t=1\), and \(\Delta t=0.001\) for \(0.1\leq z\leq0.9\). It is clear that we have achieved self-explanatory results as compared to the outcomes obtained from IRKM [31]. Table 6 reports the present experimental results at \(t=1\) with \(\Delta t=h^{2}\) and \(\alpha=0.25,0.5,0.75\). In Table 7, the error norms \(L_{2}\) and \(L_{\infty}\) are tabulated for \(\alpha=0.2, 0.5, 0.8\) with the variation of time t. Figure 1 depicts the physical behavior of exact and numerical solutions at different time levels for \(N=80\), \(\alpha=0.6\), and \(\Delta t=0.001\) in the domain \(z\in[0,1]\). The three-dimensional plots given in Fig. 2 show the accuracy of the proposed scheme for \(\alpha=0.6\), \(N=80\), \(\Delta t=0.001 \), and \(t=0.2\). In Fig. 3 the spline solution at different time stages is displayed in a single frame when \(-1\leq z\leq2\). The 3D plots of analytical exact and numerical solutions for \(N=100\), \(\alpha =0.4\), \(t=0.2\), and \(\Delta t= 0.001\) are shown in Fig. 4. Figure 5 shows the numerical results with variation of α for \(N=20\), \(t=0.4 \), and \(0\leq z\leq1\).
Exact and numerical solutions for Example 1 when \(N=80\), \(\Delta t =0.001\), \(\alpha=0.6\), and \(0\leq z \leq 1\)
Exact and numerical solutions for Example 1 when \(N=80\), \(\alpha=0.6\), \(t=0.2\), and \(\Delta t= 0.001\)
Exact and approximate solutions for Example 1 when \(N=60\), \(\Delta t =0.001\), \(\alpha=0.4\), and \(-1\leq z \leq 2\)
Exact and numerical solutions for Example 1 when \(N=100\), \(\alpha=0.4\), \(t=0.2\), \(\Delta t= 0.01\), and \(-4\leq z \leq5\)
Numerical solution for Example 1 when \(N=20\), \(t =0.4\), \(0\leq z \leq1\) with variation of α
Problem 2
Consider the following time fractional ACE [29]:
The source term \(f(z,t)\) on the right-hand side is given by
where \(E_{\beta, \gamma}(\zeta)\), the Mittag–Leffler function, is defined as [29]
The initial and boundary conditions can be derived from the given exact solution \(z (1-z^{2})^{3}t^{2}E_{1,3}(t)\). To affirm the impact and applicability of the proposed approach, the absolute error appeared in computations is given in Table 8 corresponding to different values of z using \(\alpha= 0.5\), \(n=10\), \(t=0.1\), \(\Delta t= 0.001\), and \(0 \leq z \leq1\). In Table 9 the \(L_{2}\) norm is presented against different values of α and t for \(h^{-3}\) in the domain \(z\in[-1,1]\). The graphic representation of exact and approximate solutions is shown in Fig. 6 subject to \(N=100\), \(\Delta t =0.001\)\(\alpha=0.6\), and \(-1\leq z \leq1\). The 3D plots of exact and approximate solution for Example 2 are shown in Figs. 7–8.
Exact and approximate solutions for Example 2 when \(N=100\), \(\Delta t =0.001\), \(\alpha=0.6\), and \(-1\leq z \leq 1\)
Exact and approximate solutions for Example 2 when \(N=16\), \(\alpha=0.8\), \(t=1\), \(\Delta t= 0.001\), and \(0\leq z \leq 1\)
Exact and approximate solutions for Example 2 when \(N=40\), \(\alpha=0.3\), \(t=1\), \(\Delta t= 0.001\), and \(-1\leq z \leq 1\)
Problem 3
Consider the following time fractional ACE [32]:
where the forcing term on the right-hand side is given by
The initial and boundary conditions are
The exact solution of the given problem is \(t^{2} \sin(z)\). In Table 10 the exact and numerical solutions have been showcased for \(\alpha=0.9\), \(t=0.1\), \(\Delta t=0.001\), and \(z\in[0,\pi]\). Moreover, the absolute computational error has also been reported using the same choice of parameters. Here we have intentionally taken \(n=10\) to demonstrate the efficiency of our method. In Figs. 9, 10, 11 the 2D and 3D plots of exact and numerical solutions are displayed. We can see that even with a large grid spacing, our numerical scheme can efficiently approximate the cubic B-spline solution for time fractional ACE.
Exact and numerical solutions for Example 3 when \(N=100\), \(t=1\), \(\Delta t =0.0001\), \(\alpha=0.8\), and \(-\pi\leq z \leq\pi\)
Exact and approximate solutions for Example 3 when \(N=20\), \(\alpha=0.4\), \(t=0.3\), \(\Delta t= 0.001\), and \(-\pi\leq z \leq\pi\)
Exact and approximate solutions for Example 3, when \(N=80\), \(\alpha=0.5\), \(t=1\), \(\Delta t= 0.001\) and \(-2\pi\leq z \leq2\pi\)
6 Concluding remarks
We conclude this work by the following remarks:
An efficient algorithm based on redefined cubic B-spline collocation approach has been presented for approximate solution of time fractional Allen–Cahn equation.
The proposed scheme engages usual finite forward difference formulation and a redefined set of cubic B-spline functions for temporal and spatial discretizations, respectively.
The unconditional stability of the proposed method has been proved rigorously.
The computational order of convergence is conformable with the theoretical estimations.
The numerical simulation has been run for three test examples, which show that the proposed scheme can efficiently be employed for numerical treatment of time fractional problems.
References
Tariq, H., Akram, G.: New approach for exact solutions of time fractional Cahn–Allen equation and time fractional Phi-4 equation. Phys. A, Stat. Mech. Appl. 473, 352–362 (2017)
Lu, B.: The first integral method for some time fractional differential equations. J. Math. Anal. Appl. 395(2), 684–693 (2012)
He, J.-H., Wu, X.-H.: Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 30(3), 700–708 (2006)
Gepreel, K.A., Omran, S.: Exact solutions for nonlinear partial fractional differential equations. Chin. Phys. B 21(11), Article ID 110204 (2012)
Liu, W., Chen, K.: The functional variable method for finding exact solutions of some nonlinear time-fractional differential equations. Pramana 81(3), 377–384 (2013)
Bulut, H., Baskonus, H.M., Pandir, Y.: The modified trial equation method for fractional wave equation and time fractional generalized Burgers equation. Abstr. Appl. Anal., 2013, Article ID 636802 (2013)
Zheng, B., Wen, C.: Exact solutions for fractional partial differential equations by a new fractional sub-equation method. Adv. Differ. Equ. 2013(1), Article ID 199 (2013)
Taghizadeh, N., Mirzazadeh, M., Rahimian, M., Akbari, M.: Application of the simplest equation method to some time-fractional partial differential equations. Ain Shams Eng. J. 4(4), 897–902 (2013)
Sahoo, S., Ray, S.S.: New solitary wave solutions of time-fractional coupled Jaulent–Miodek equation by using two reliable methods. Nonlinear Dyn. 85(2), 1167–1176 (2016)
Tariq, H., Akram, G.: New traveling wave exact and approximate solutions for the nonlinear Cahn–Allen equation: evolution of a nonconserved quantity. Nonlinear Dyn. 88(1), 581–594 (2017)
Prüss, J., Wilke, M.: Maximal \(L_{\mathrm{p}}\)-regularity and long-time behaviour of the non-isothermal Cahn–Hilliard equation with dynamic boundary conditions. In: Partial Differential Equations and Functional Analysis, pp. 209–236. Birkhäuser, Basel (2006)
Allen, S.M., Cahn, J.W.: A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 27(6), 1085–1095 (1979)
Liu, C., Shen, J.: A phase field model for the mixture of two incompressible fluids and its approximation by a Fourier-spectral method. Phys. D, Nonlinear Phenom. 179(3–4), 211–228 (2003)
Yue, P., Zhou, C., Feng, J.J., Ollivier-Gooch, C.F., Hu, H.H.: Phase-field simulations of interfacial dynamics in viscoelastic fluids using finite elements with adaptive meshing. J. Comput. Phys. 219(1), 47–67 (2006)
Atangana, A., Akgül, A.: Can transfer function and Bode diagram be obtained from Sumudu transform. Alex. Eng. J. (2020). https://doi.org/10.1016/j.aej.2019.12.028
Atangana, A., Gómez-Aguilar, J.F.: Numerical approximation of Riemann–Liouville definition of fractional derivative: from Riemann–Liouville to Atangana–Baleanu. Numer. Methods Partial Differ. Equ. 34(5), 1502–1523 (2018)
Sheikh, N.A., Ali, F., Khan, I., Saqib, M.: A modern approach of Caputo–Fabrizio time-fractional derivative to MHD free convection flow of generalized second-grade fluid in a porous medium. Neural Comput. Appl. 30(6), 1865–1875 (2018)
Atangana, A., Akgül, A., Owolabi, K.M.: Analysis of fractal fractional differential equations. Alex. Eng. J. (2020). https://doi.org/10.1016/j.aej.2020.01.005
Akgül, E.K.: Solutions of the linear and nonlinear differential equations within the generalized fractional derivatives. Chaos, Interdiscip. J. Nonlinear Sci. 29(2), Article ID 023108 (2019)
Amin, M., Abbas, M., Iqbal, M.K., Baleanu, D.: Non-polynomial quintic spline for numerical solution of fourth-order time fractional partial differential equations. Adv. Differ. Equ. 2019(1), Article ID 183 (2019)
Esen, A., Yagmurlu, N.M., Tasbozan, O.: Approximate analytical solution to time-fractional damped Burger and Cahn–Allen equations. Appl. Math. Inf. Sci. 7(5), 1951–1956 (2013)
Jafari, H., Tajadodi, H., Baleanu, D.: Application of a homogeneous balance method to exact solutions of nonlinear fractional evolution equations. J. Comput. Nonlinear Dyn. 9(2), Article ID 021019 (2014)
Hamed, M.A., Nepomnyashchy, A.A.: Domain coarsening in a subdiffusive Allen–Cahn equation. Phys. D, Nonlinear Phenom. 308, 52–58 (2015)
Yasar, E., Giresunlu, I.B.: The \((G'/G, 1/G)\)-expansion method for solving nonlinear space-time fractional differential equations. Pramana J. Phys. 87, Article ID 17 (2016)
Güner, O., Bekir, A., Cevikel, A.C.: A variety of exact solutions for the time fractional Cahn–Allen equation. Eur. Phys. J. Plus 130(7), Article ID 146 (2015)
Zhai, S., Weng, Z., Feng, X.: Fast explicit operator splitting method and time-step adaptivity for fractional non-local Allen–Cahn model. Appl. Math. Model. 40(2), 1315–1324 (2016)
Akagi, G., Schimperna, G., Segatti, A.: Fractional Cahn–Hilliard, Allen–Cahn and porous medium equations. J. Differ. Equ. 261(6), 2935–2985 (2016)
Hou, T., Tang, T., Yang, J.: Numerical analysis of fully discretized Crank–Nicolson scheme for fractional-in-space Allen–Cahn equations. J. Sci. Comput. 72(3), 1214–1231 (2017)
Li, Z., Wang, H., Yang, D.: A space-time fractional phase-field model with tunable sharpness and decay behavior and its efficient numerical simulation. J. Comput. Phys. 347, 20–38 (2017)
Hosseini, K., Bekir, A., Ansari, R.: New exact solutions of the conformable time-fractional Cahn–Allen and Cahn–Hilliard equations using the modified Kudryashov method. Optik, Int. J. Light Electron Opt. 132, 203–209 (2017)
Sakar, M.G., Saldir, O., Erdogan, F.: An iterative approximation for time-fractional Cahn–Allen equation with reproducing kernel method. Comput. Appl. Math. 37(5), 5951–5964 (2018)
Liu, H., Cheng, A., Wang, H., Zhao, J.: Time-fractional Allen–Cahn and Cahn–Hilliard phase-field models and their numerical investigation. Comput. Math. Appl. 76(8), 1876–1892 (2018)
Yin, B., Liu, Y., Li, H., He, S.: Fast algorithm based on TT-M FE system for space fractional Allen–Cahn equations with smooth and non-smooth solutions. J. Comput. Phys. 379, 351–372 (2019)
Inc, M., Yusuf, A., Aliyu, A.I., Baleanu, D.: Time-fractional Cahn–Allen and time-fractional Klein–Gordon equations: Lie symmetry analysis, explicit solutions and convergence analysis. Phys. A, Stat. Mech. Appl. 493, 94–106 (2018)
Khalid, N., Abbas, M., Iqbal, M.K., Baleanu, D.: A numerical algorithm based on modified extended B-spline functions for solving time-fractional diffusion wave equation involving reaction and damping terms. Adv. Differ. Equ. 2019(1), Article ID 378 (2019)
Khalid, N., Abbas, M., Iqbal, M.K.: Non-polynomial quintic spline for solving fourth-order fractional boundary value problems involving product terms. Appl. Math. Comput. 349, 393–407 (2019)
Iqbal, M.K., Abbas, M., Khalid, N.: New cubic B-spline approximation for solving non-linear singular boundary value problems arising in physiology. Commun. Math. Appl. 9(3), 377–392 (2018)
Mittal, R.C., Jain, R.K.: Redefined cubic B-splines collocation method for solving convection–diffusion equations. Appl. Math. Model. 36(11), 5555–5573 (2012)
Sharifi, S., Rashidinia, J.: Numerical solution of hyperbolic telegraph equation by cubic B-spline collocation method. Appl. Math. Comput. 281, 28–38 (2016)
Boyce, W.E., DiPrima, R.C., Meade, D.B.: Elementary Differential Equations and Boundary Value Problems, 9th edn. Wiley, New York (1992)
Kadalbajoo, M.K., Arora, P.: B-spline collocation method for the singular-perturbation problem using artificial viscosity. Comput. Math. Appl. 57(4), 650–663 (2009)
de Boor, C.: On the convergence of odd-degree spline interpolation. J. Approx. Theory 1(4), 452–463 (1968)
Hall, C.A.: On error bounds for spline interpolation. J. Approx. Theory 1(2), 209–218 (1968)
Acknowledgements
The authors are grateful to the anonymous reviewers for their helpful and valuable comments and suggestions for improvement of this manuscript. We also thank Dr. Muhammad Amin for his assistance in proofreading of the manuscript.
Availability of data and materials
Not applicable.
Authors’ information
Nauman Khalid is PhD scholar, Muhammad Abbas is Associate Professor, Muhammad Kashif Iqbal is Assistant Professor, and Dumitru Baleanu is Professor.
Funding
No funding is available for this research. We are grateful to Springer Open on providing full wavier for this manuscript.
Author information
Authors and Affiliations
Contributions
All authors equally contributed to this work. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Khalid, N., Abbas, M., Iqbal, M.K. et al. A numerical investigation of Caputo time fractional Allen–Cahn equation using redefined cubic B-spline functions. Adv Differ Equ 2020, 158 (2020). https://doi.org/10.1186/s13662-020-02616-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02616-x