Abstract
Rossby waves, one of significant waves in the solitary wave, have important theoretical meaning in the atmosphere and ocean. However, the previous studies on Rossby waves commonly were carried out in the zonal area and could not be applied directly to the spherical earth. In order to overcome the problem, the research on (\(3+1\))-dimensional Rossby waves in the paper is placed into the spherical area, and some new analytical solutions of (\(3+1\))-dimensional Rossby waves are given through the classic Lie group method. Finally, the dissipation effect is analyzed in the sense of the above mentioned new analytical solutions. The new solutions on (\(3+1\))-dimensional Rossby waves have important value for understanding the propagation of Rossby waves in the rotating earth with the influence of dissipation.
Similar content being viewed by others
1 Introduction
As is well known, Rossby waves play a central role in the atmosphere and ocean, which depicts an essential phenomenon. The oceans’s response to the atmosphere change and climate change can be determined by Rossby waves. In addition, Rossby waves have significant theoretical meaning and real value in the atmosphere and ocean. In recent years, more and more researchers have focused on the study of Rossby waves [1,2,3,4]. Many studies on Rossby waves have been conducted in the zonal area, and many meaningful results have been achieved [5, 6]. However, as everyone knows, the propagation of Rossby waves happens in the earth which is a spherical area [7], so the above mentioned achievements could not be directly applied. It is necessary to discuss the propagation characteristic of (\(3+1\))-dimensional Rossby waves in the spherical area under the influence of dissipation. Here, in order to overcome the problem, our research is carried out in cylindrical coordinate, which better matches with the real condition.
With the development of soliton theory, Rossby waves have been becoming an important research direction in the field of the nonlinear partial differential [8,9,10]. In recent years, some weakly nonlinear models for the evolution of Rossby waves have been extensively studied [11,12,13]. More importantly, some methods are found to study the nonlinear models [14,15,16,17,18] and some significant properties are discussed [19,20,21,22,23]. In the past, Rossby waves were often studied in the zonal area. However, Rossby waves are prominently affected via the rotation effect of the earth. Therefore, in order to study some propagation characteristics of Rossby waves, we use the (\(3+1\))-dimensional quasi-geostrophic vorticity equation with dissipation effect in the cylindrical coordinate to describe the dynamic behavior of Rossby waves.
In this paper, the (\(3+1\))-dimensional Rossby waves with dissipation effect in cylindrical coordinate will be discussed through the classic Lie group method. In Sect. 2, we analyze the (\(3+1\))-dimensional Rossby waves with dissipation effect in cylindrical coordinate by using the classic Lie group method. In Sect. 3, the solution of the (\(3+1\))-dimensional Rossby waves with dissipation effect in cylindrical coordinate can be obtained. In addition, some conclusions are placed in Sect. 4.
2 Symmetry analysis for the (\(3+1\))-dimensional Rossby waves with dissipation effect in cylindrical coordinate
In Ref. [24], the (\(2+1\))-dimensional model for Rossby waves is researched based on the classical Lie group approach. Then, the (\(3+1\))-dimensional model for Rossby waves is analyzed by Myagkov [25]. In Ref. [26], the authors adopt the plane polar coordinate to study the (\(2+1\))-dimensional model
and discuss the dynamic characteristics of the model in rotating barotropic atmosphere. But the dissipation effect is ignored.
In the paper, we analyze the (\(3+1\))-dimensional quasi-geostrophic vorticity equation with dissipation effect in cylindrical coordinate
where ϕ describes the dimensionless stream function, \(\beta = \beta _{0}(L^{2}/U)\), and \(\beta _{0}= (\omega _{0}/R_{0})\cos \varphi _{0}\), in which \(\omega _{0}\) and \(R_{0}\) are the angular frequency of the Earth’s rotation and the Earth’s radius, respectively, L is the characteristic horizontal length, \(\varphi _{0}\) depicts the latitude, U is velocity scales and α depicts the dissipation coefficient.
In addition, we introduce the vector field
The first order prolongation operator and the second order prolongation operator can be given as follows:
Similarly, the third order prolongation operator can be defined as
Substituting Eq. (2) into Eq. (1), it is easy to conclude that
based on the Lie group method.
By comparing the coefficient of \(\phi _{\rho }\), \(\phi _{\theta }\), \(\phi _{z}\), \(\phi _{t}\), \(\phi _{\rho \theta }\), \(\phi _{\rho z}\), \(\phi _{\rho t}\), \(\phi _{\rho \theta z}\), we get
where \(g_{1}(t),g_{2}(t), \ldots, g_{5}(t)\) are arbitrary functions of t and \(C_{1},C_{2}, \ldots, C_{10}\) are arbitrary constants.
Therefore, the Lie algebra of Eq. (1) can be given by
where \(g_{1}\), \(g_{2}\), \(g_{3}\), \(g_{4}\), \(g_{5}\) are continuous functions and the vector field V is the Lie symmetry group generator. The calculation and proof of Eq. (4) can be taken into account and all applications of the symmetry group below are proved by substituting into Eq. (1) directly.
Assume \(\phi _{s}(t,\rho,\theta,z)\) is a solution of Eq. (1). According to operators \(V_{6}\), \(V_{7}\), \(V_{8}\), \(V_{9}\), \(V_{10}\), the new solution can be written as follows:
Thus, we have
according to the nontrivial transformation of Eq. (5). It is well known that new exact solutions for the differential equation can be found through the classic Lie symmetry group when a particular solution is known [27].
3 The new solution of the (\(3+1\))-dimensional Rossby waves with dissipation effect in cylindrical coordinate
In order to obtain the solution of the (\(3+1\))-dimensional dissipation Rossby waves in cylindrical coordinate, it is important to seek the solution of the (\(2+1\))-dimensional dissipation Rossby waves in cylindrical coordinate. Next, we discuss the (\(2+1\))-dimensional quasi-geostrophic vorticity equation with dissipation effect in cylindrical coordinate
When dissipation does not exist, we first suppose
where c is a constant and denotes the phase speed of the wave. Equation (8) implies that
Based on the above transform, Eq. (7) becomes
According to a complex calculation, we acquire
where \(C_{1}\), \(C_{2}\), c express arbitrary constants. Substituting (8) into (10), we have
In the following, we respect the influence of dissipation on Eq. (7). Defining \(\alpha \ll 1\) and \(\alpha \ll \beta \), we suppose
where \(\phi _{0}=\phi _{0}(\alpha t)\) varies slowly with time. Substituting Eq. (11) into Eq. (7), we get
Suppose
and
we have
by substituting Eq. (14) into Eq. (12).
Then, setting
we have
It is easy to derive that the solution of Eq. (19) has the following form
where \(\phi _{0}=C_{1}C_{2}\). Based on Eq. (11) and Eq. (17), we acquire
Next, let
and substituting Eq. (22) into Eq. (19), we acquire
where
The solvability condition of Eq. (23) is
where
The solution of Eq. (25) is easy to acquire in the following form
in the case of \(G(\pm \infty)=0\). Equation (26) can be rewritten as
Substituting Eq. (27) into Eq. (24), we obtain
where \(\bar{\phi }_{0}=\phi _{0}\). Hence, we have
It is simple to prove that Eq. (29) is the approximate analytical solution of Eq. (7). Thus, the new (\(3+1\))-dimensional dissipation Rossby waves solution in cylindrical coordinate can be given by
where
4 Discussion and conclusion
In this section, the solution of the (\(3+1\))-dimensional dissipation Rossby waves can be discussed relying on Eq. (30).
When \(g_{2}(t)=\cos t\), \(g_{4}(t)=\cos t\), \(g_{5}(t)=\sin t\), Eq. (30) can be rewritten as
where
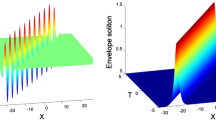
Obviously, Rossby waves were established in the zonal area and could not be used directly to the spherical earth in the previous research. However, in this paper, we get the solution of the (\(3+1\))-dimensional dissipation Rossby waves by using the classic Lie group method in cylindrical coordinate, and the new solution overcomes the problem. According to theoretical analysis, we can make the following conclusion: In the spherical earth, the dissipation effect could give rise to a decrease in amplitude \(e^{-\alpha t}\), where α denotes the dissipation coefficient from Eq. (31).
References
Zhao, B.J., Wang, R.Y., Sun, W.J., Yang, H.W.: Combined ZK-mZK equation for Rossby solitary waves with complete Coriolis force and its conservation laws as well as exact solutions. Adv. Differ. Equ. 2018, 42 (2018)
Zhang, R.G., Yang, L.G., Song, J., Yang, H.L.: (\(2+1\))-dimensional Rossby waves with complete Coriolis force and its solution by homotopy perturbation method. Comput. Math. Appl. 73, 1996–2003 (2017)
Lu, C.N., Fu, C., Yang, H.W.: Time-fractional generalized Boussinesq equation for Rossby solitary waves with dissipation effect in stratified fluid and conservation laws as well as exact solutions. Appl. Math. Comput. 327, 104–116 (2018)
Yang, H.W., Xu, Z.H., Yang, D.Z., Feng, X.R., Yin, B.S., Dong, H.H.: ZK-Burgers equation for three-dimensional Rossby solitary waves and its solutions as well as chirp effect. Adv. Differ. Equ. 2016, 167 (2016)
Guo, M., Zhang, Y., Wang, M., Chen, Y.D., Yang, H.W.: A new ZK-ILW equation for algebraic gravity solitary waves in finite depth stratified atmosphere and the research of squall lines formation mechanism. Comput. Math. Appl. 75, 5468–5478 (2018)
Fu, C., Lu, C.N., Yang, H.W.: Time-space fractional (\(2+1\))-dimensional nonlinear Schrödinger equation for envelope gravity waves in baroclinic atmosphere and conservation laws as well as exact solutions. Adv. Differ. Equ. 2018, 56 (2018)
Haurwitz, B.: The motion of atmospheric disturbances on the spherical Earth. J. Mar. Res. 3, 254–267 (1940)
Yong, X.L., Ma, W.X., Huang, Y.H., Liu, Y.: Lump solutions to the Kadomtsev–Petviashvili I equation with a self-consistent source. Comput. Math. Appl. 75, 3414–3419 (2018)
Yang, X.J., Gao, F., Srivastava, H.M.: Exact travelling wave solutions for the local fractional two-dimensional Burgers-type equations. Comput. Math. Appl. 73, 203–210 (2017)
Guo, M., Fu, C., Zhang, Y., Liu, J.X., Yang, H.W.: Study of ion-acoustic solitary waves in a magnetized plasma using the three-dimensional time-space fractional Schamel-KdV equation. Complexity 2018, 6852548 (2018)
Yang, X.J., Gao, F., Srivastava, H.M.: A new computational approach for solving nonlinear local fractional PDEs. J. Comput. Appl. Math. 339, 285–296 (2018)
Zhao, H.Q., Ma, W.X.: Mixed lump-kink solutions to the KP equation. Comput. Math. Appl. 74, 1399–1405 (2017)
Zhang, J.B., Ma, W.X.: Mixed lump-kink solutions to the BKP equation. Comput. Math. Appl. 74, 591–596 (2017)
Tao, M.S., Dong, H.H.: Algebro-geometric solutions for a discrete integrable equation. Discrete Dyn. Nat. Soc. 2017, 5258375 (2017)
Ma, W.X., Zhou, Y.: Lump solutions to nonlinear partial differential equations via Hirota bilinear forms. J. Differ. Equ. 264, 2633–2659 (2018)
Xu, X.X.: A deformed reduced semi-discrete Kaup–Newell equation, the related integrable family and Darboux transformation. Appl. Math. Comput. 251, 275–283 (2015)
Li, X.Y., Zhao, Q.L., Li, Y.X., Dong, H.H.: Binary Bargmann symmetry constraint associated with 3 × 3 discrete matrix spectral problem. J. Nonlinear Sci. Appl. 8, 496–506 (2015)
Bai, Z.B., Zhang, S., Sun, S.J., Yin, C.: Monotone iterative method for fractional differential equations. Electron. J. Differ. Equ. 2016, 1 (2016)
Gu, X., Ma, W.X., Zhang, W.Y.: Two integrable Hamiltonian hierarchies in \(\mathrm{sl}(2,R)\) and \(\mathrm{so}(3,R)\) with three potentials. Appl. Math. Comput. 14, 053512 (2017)
Wang, H., Wang, Y.H., Dong, H.H.: Interaction solutions of a (\(2+1\))-dimensional dispersive long wave system. Comput. Math. Appl. 75, 2625–2628 (2018)
Ma, W.X., Yong, X.L., Zhang, H.Q.: Diversity of interaction solutions to the (\(2+1\))-dimensional ito equation. Comput. Math. Appl. 75, 289–295 (2018)
Feng, B.F., Maruno, K., Ohta, Y.: A two-component generalization of the reduced Ostrovsky equation and its integrable semi-discrete analogue. J. Phys. A, Math. Theor. 50, 055201 (2017)
McAnally, M., Ma, W.X.: An integrable generalization of the D-Kaup–Newell soliton hierarchy and its bi-Hamiltonian reduced hierarchy. Appl. Math. Comput. 323, 220–227 (2018)
Huang, F., Lou, S.Y.: Analytical investigation of Rossby waves in atmospheric dynamics. Phys. Lett. A 320, 428–437 (2004)
Kudryavtsev, A.G., Myagkov, N.N.: Symmetry group application for the (\(3+1\))-dimensional Rossby waves. Phys. Lett. A 375, 586–588 (2011)
Chao, J.P., Huang, R.X.: The cnoidal waves of rotating barotropic atmosphere. Sci. Sin. 23, 1266–1277 (1980)
Olver, P.: Applications of Lie Groups to Differential Equations. Springer, Berlin (1986)
Funding
This work was supported by the Natural Science Foundation of Shandong Province of China (No. ZR2018MA017), China Postdoctoral Science Foundation funded project (No. 2017M610436).
Author information
Authors and Affiliations
Contributions
The authors declare that the study was realized in collaboration with the same responsibility. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ren, Y., Tao, M., Dong, H. et al. Analytical research of (\(3+1\))-dimensional Rossby waves with dissipation effect in cylindrical coordinate based on Lie symmetry approach. Adv Differ Equ 2019, 13 (2019). https://doi.org/10.1186/s13662-019-1952-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-1952-4