1 Introduction

Fractional operators have been more and more applied to model acoustics and thermal systems, rheology and modeling of materials and mechanical systems, signal processing and systems identification, control and robotics, and so on [1–5]. Many researchers have considerable interest in the existence of solutions and numerical methods for fractional differential equations [2, 6–13], the topics that have been developing rapidly over the last few decades. We are interested in designing an iteration method for solving the spatial fractional coupled nonlinear Schrödinger (CNLS) equations

$$\begin{aligned} \textstyle\begin{cases} i\frac{\partial u(x,t)}{\partial t}+\gamma (-\Delta )^{\frac{\alpha }{2}}u(x,t)+\rho (\vert u \vert ^{2}+\beta \vert v \vert ^{2})u(x,t) = 0, \\ i\frac{\partial v(x,t)}{\partial t}+\gamma (-\Delta )^{\frac{\alpha }{2}}v(x,t)+\rho (\vert v \vert ^{2}+\beta \vert u \vert ^{2})v(x,t) = 0, \end{cases}\displaystyle (x,t)\in (x_{\mathrm{{L}}},x_{\mathrm{{R}}})\times (0,\theta ) \end{aligned}$$
(1.1)

under the boundary values and initial conditions

$$\begin{aligned} \textstyle\begin{cases} u(x,0)=u_{0}(x),& v(x,0)=v_{0}(x), \\ u(x_{\mathrm{{L}}},t)=u(x_{\mathrm{{R}}},t)=0,&v(x_{\mathrm{{L}}},t)=v(x_{\mathrm{{R}}},t)=0. \end{cases}\displaystyle \end{aligned}$$

Here and in the sequel, we use \(i=\sqrt{-1}\) to denote the imaginary unit, \(1< \alpha < 2\) and \(\gamma , \rho >0, \beta \geq 0\) are all constants. The fractional Laplacian [1] can be characterized as

$$\begin{aligned} -(-\Delta )^{\frac{\alpha }{2}}u(x,t)=-\mathcal{F}^{(-1)} \bigl(\vert \xi \vert ^{\alpha }\mathcal{F} \bigl(u(x,t) \bigr) \bigr), \end{aligned}$$

where \(\mathcal{F}\) denotes the Fourier transform acting on the spatial variable x. Moreover, it is just equivalent to the Riesz fractional derivative [2], say the following equation:

$$ -(-\Delta )^{\frac{\alpha }{2}}u(x,t)=\frac{\partial ^{\alpha }}{\partial \vert x \vert ^{\alpha }}u(x,t)=-\frac{1}{2\cos \frac{\pi \alpha }{2}} \bigl[_{-\infty }D_{x}^{\alpha }u(x,t)+{}_{x}D_{+\infty }^{\alpha }u(x,t) \bigr], $$

where \({}_{-\infty }D_{x}^{\alpha }u(x,t)\) and \({}_{x}D_{+\infty }^{\alpha }u(x,t)\) are the left-sided and the right-sided Riemann–Liouville fractional derivatives defined as follows:

$$\begin{aligned} \textstyle\begin{cases} _{-\infty }D_{x}^{\alpha }u(x,t)=\frac{1}{\Gamma (2-\alpha )}\cdot \frac{d^{2}}{dx^{2}}\int_{x}^{x_{\mathrm{{R}}}}(\xi -x)^{1-\alpha }u(\xi ,t)\,d\xi , \\ _{x}D_{+\infty }^{\alpha }u(x,t)= \frac{1}{\Gamma (2-\alpha )}\cdot \frac{d^{2}}{dx^{2}}\int_{x_{\mathrm{{L}}}}^{x}(x-\xi )^{1-\alpha }u(\xi ,t)\,d\xi , \end{cases}\displaystyle \end{aligned}$$

here and in the sequel \(\Gamma (\cdot )\) is the Gamma function.

The spatial fractional Schrödinger equations have attracted wide attention in recent years. Their classical forms describe the evolution of microscopic particles, and they arise in the path integral over the Brownian motion. In [3, 4], Laskin extended firstly the path integral method to obtain the spatial fractional Schrödinger equations, which comes from the Brownian motion to the Lévy process. Guo and Xu [5] studied some physical applications of fractional Schrödinger equations. The existence of a global smooth solution of fractional nonlinear Schrödinger equations was discussed by Guo et al. [14]. Many authors have concentrated on the solution of fractional Schrödinger equations in one dimension [15–17]. Since one of the major characteristics of the fractional differential operator is being nonlocal, it is pretty hard to gain the true solution of fractional differential equations generally. Therefore, the numerical methods (e.g., some splitting iteration methods) have become usable and powerful tools in order to understand the behaviors of fractional differential equations. Recently, another approach based on the study of Lie symmetries of fractional differential equations can be found in the papers [18, 19].

From what we known, there exist certain studies on numerical methods for the fractional Schrödinger equations. The Crank–Nicolson difference scheme for the coupled nonlinear fractional Schrödinger equations was proposed by Wang et al. [20] in 2013. Subsequently, Atangana and Cloot [21] studied its stability and convergence for the space fractional variable-order Schrödinger equations. Since the scheme is nonlinearly implicit and coupled in computation, the iteration costs at each step are expensive. Moreover, the nonlocal property of the fractional operator resulted in dense or full matrices. Consequently, with the fractional centered difference formula, Wang et al. [22, 23] proposed recently an implicit conservative difference scheme, which is unconditionally stable, to discretize the spatial fractional CNLS equations. The coefficient matrix A of the discretized linear system about Eqs. (1.1) is \(D+\widetilde{T}\), the sum of a real diagonal matrix D and a complex symmetric Toeplitz matrix T̃, which is just the real symmetric Toeplitz matrix T plus an imaginary-identity matrix Ĩ, \(\widetilde{T}=T+iI\). In view of the coefficient matrix being full or dense, the Gaussian elimination method is unfeasible because of its heavy computational and storage load. The computational costs of the Krylov subspace iterations [24–27] when solving the discretized linear system are quite expensive. Moreover, their convergence rates tend to be considerably worse.

It is appropriated that the coefficient matrix \(A=D+\widetilde{T}\) is non-Hermitian but positive definite. And then those derived iteration methods based on the famous HSS can be used to solve this complex symmetric and non-Hermitian positive definite linear system \(Au=b\), introduced by Bai et al. [28, 29] and so on. For example, the Hermitian and skew-Hermitian splitting (HSS) iteration method [30] was directly applied to solve the discretized linear system, and the following two variants were designed [31]:

Case I

$$\begin{aligned} \textstyle\begin{cases} (\omega I+T+D)u^{(k+\frac{1}{2})}=(\omega I-i I)u^{(k)}+b,\\ (\omega I+iI)u^{(k+1)}=(\omega I-T-D)u^{(k+\frac{1}{2})}+b, \end{cases}\displaystyle \end{aligned}$$

where ω is a given positive constant.

Case II

$$\begin{aligned} \textstyle\begin{cases} (\omega I+T)u^{(k+\frac{1}{2})}= (\omega I-D-i I)u^{(k)}+b, \\ (\omega I+D+iI)u^{(k+1)}= (\omega I-T)u^{(k+\frac{1}{2})}+b, \end{cases}\displaystyle \end{aligned}$$

where ω is a given positive constant.

Cases I and II almost shared the same computational efficiency, reported in the original paper. That is to say, at each HSS iteration step of Case I, the solution of a subsystem with the shifted matrix \(\omega I+\widetilde{I}\), where ω is the shifted parameter, made easily due to its diagonal structure. However, it is very costly and impractical in solving the shifted Hermitian subsystem with the coefficient matrix holding full and Toeplitz-like rather than Toeplitz structure. In order to reduce the complexity, the IHSS iteration or preconditioned HSS iteration [32, 33] were come up with to solve the non-Hermitian positive definite linear system. However, the tolerances (or the number of inner iterations) for the inner iterates about the first linear subsystem may be different and may be changed according to the outer iteration scheme. Therefore, the IHSS iteration is actually a nonstationary iteration method for solving the linear system, and the preconditioning matrix is not easy to choose for the preconditioned HSS iteration method. In order to overcome the disadvantages of these methods, Ran and Wang [31] proposed another HSS-like iteration method, and it is precisely stated in Case II.

In this paper, a new splitting iteration method with medium-shifting (MS) can be presented to solve the discretized linear system of the spatial fractional coupled nonlinear Schrödinger Eqs. (1.1), in which the inconvenience of alternation can be avoided. The shifted parameter is the average value of the maximum and minimum elements of the real diagonal matrix D, say medium-shifting. Theoretical analysis shows that the new iteration method is convergent. Moreover, the new splitting iteration method naturally induces a matrix splitting preconditioner. To further reduce the computational costs of the MS preconditioning matrix, we replace the real Toeplitz matrix T involved in T̃ by a circulant matrix, obtaining a preconditioner for the discretized linear system from the space fractional coupled nonlinear Schrödinger equations. Thus, the linear system can be solved economically by the fast Fourier transform. Numerical results show that the PMS iteration method can significantly improve the convergent property.

Here are some essential notations. As usual, we use \(\mathbb{C}^{M\times M}\) to denote the \(M\times M\) complex matrix set and \(\mathbb{C}^{M}\) the M-dimensional complex vector space. \(X^{*}\) represents the conjugate transpose of a matrix or a vector X. The spectral radius of the matrix A is denoted by \(\rho (A)\). \(\lambda (\cdot )\) and \(\Sigma (\cdot )\) stand for the eigenvalues set and the singular values set of a corresponding matrix, respectively. \(\Vert \cdot \Vert _{2}\) represents the Euclidean norm of a corresponding matrix. By the way, I represents an identity matrix in general.

The organization of this paper is as follows. In Sect. 2, we derive the discretized linear system from spatial fractional CNLS equation (Eq. (1.1)). In Sect. 3, we present the MS iteration method and preconditioned MS iteration method, and establish the convergent theory. The numerical results are reported in Sect. 4. Finally, we end this document with some conclusions in Sect. 5.

2 Discretization of the spatial fractional CNLS equations

In this section, the spatial fractional coupled nonlinear Schrödinger equations were discretized to a linear system. The implicit conservative difference scheme with the fractional centered difference formula, that is unconditionally stable, will be given.

Let \(\tau =\frac{\theta }{N}\) and \(h=\frac{x_{\mathrm{{R}}}-x_{\mathrm{{L}}}}{M+1}\) be the sizes of time step and spatial grid, respectively, where N and M are positive integers. A temporal and spatial partition can be defined as \(t_{n}=n\tau \), \(n=0,1,\ldots ,N\), and \(x_{j}=x_{\mathrm{{L}}}+jh\), \(j=0,1,\ldots ,M+1\). The corresponding numerical solutions are defined by \(u_{j}^{n}\thickapprox u(x_{j},t_{n})\) and \(v_{j}^{n}\thickapprox v(x_{j},t_{n})\). In terms of the fractional centered difference [34], the fractional Laplacian \((-\Delta )^{\frac{\alpha }{2}}\) in the truncated bounded domain can be discretized as

$$ (-\Delta )^{\frac{\alpha }{2}}u(x_{j})=-\frac{\partial ^{\alpha }}{\partial \vert x \vert ^{\alpha }}u_{j}= \frac{1}{h^{\alpha }}\sum_{k=1}^{M}c_{j-k}^{(\alpha )}u_{k}+ \mathcal{O} \bigl(h^{2} \bigr), $$

where \(c_{k}^{(\alpha )}\) (\(k=0,1,\ldots ,M-1\)) are defined by

$$ c_{k}^{(\alpha )}=\frac{(-1)^{k}\Gamma (\alpha +1)}{\Gamma (\alpha /{2-k+1})\Gamma (\alpha /{2+k+1})}. $$

It is clear that \(c_{k}^{(\alpha )} \) satisfy the following properties:

$$\begin{aligned} \textstyle\begin{cases} c_{0}^{(\alpha )}\geq 0, \\ c_{k}^{(\alpha )}=c_{-k}^{(\alpha )}\leq 0,\quad k=1,2,\ldots \,, \\ \sum_{k=-\infty ,k\neq 0}^{+\infty }\vert c_{k}^{(\alpha )} \vert =c_{0}^{(\alpha )}. \end{cases}\displaystyle \end{aligned}$$

Then the following implicit difference scheme for the spatial fractional CNLS Eqs. (1.1) can be obtained:

$$\begin{aligned} \textstyle\begin{cases} i\frac{u_{j}^{n+1}-u_{j}^{n-1}}{2\tau }+\frac{\gamma }{h^{\alpha }}\sum_{k=1}^{M} c_{j-k}^{(\alpha )}(\frac{u_{k}^{n+1}+u_{k}^{n-1}}{2}) +\rho (\vert u_{j}^{n} \vert ^{2}+\beta \vert v_{j}^{n} \vert ^{2})\frac{u_{j}^{n+1}+u_{j}^{n-1}}{2}=0,\\ i\frac{v_{j}^{n+1}-v_{j}^{n-1}}{2\tau }+\frac{\gamma }{h^{\alpha }}\sum_{k=1}^{M} c_{j-k}^{(\alpha )}(\frac{v_{k}^{n+1}+v_{k}^{n-1}}{2}) +\rho (\vert v_{j}^{n} \vert ^{2}+\beta \vert u_{j}^{n} \vert ^{2})\frac{v_{j}^{n+1}+v_{j}^{n-1}}{2}=0, \end{cases}\displaystyle \end{aligned}$$
(2.1)

where \(j=1, 2, \ldots , M, n=1,2,\ldots ,N-1\), and it has been proved that scheme (2.1) conserves the discrete mass and energy, and is unconditionally stable and convergent with the order \(\mathcal{O}(\tau ^{2}+h^{2})\) in the discrete \(l^{2}\)-norm [22, 23]. By the boundary values and initial conditions, we have

$$ u_{j}^{0}=u_{0}(x_{j}),\qquad v_{j}^{0}=v_{0}(x_{j}),\qquad u_{0}^{n}=u_{M+1}^{n}=0,\qquad v_{0}^{n}=v_{M+1}^{n}=0. $$

Moreover, the first step can be obtained by some second or higher order time integrators. The structure of the first difference equation in (2.1) is the same as that of the second one. By introducing two M-dimensional vectors

$$\begin{aligned} u^{n+1}= \bigl[u_{1}^{n+1},\ldots ,u_{M}^{n+1} \bigr]^{T},\qquad b^{n+1}= \bigl[b_{1}^{n+1},\ldots ,b_{M}^{n+1} \bigr]^{T}, \end{aligned}$$

and two parameters

$$\begin{aligned} \mu =\frac{\gamma \tau }{h^{\alpha }},\qquad d_{j}^{n+1}=\rho \tau \bigl( \bigl\vert u_{j}^{n} \bigr\vert ^{2}+\beta \bigl\vert v_{j}^{n} \bigr\vert ^{2} \bigr) \end{aligned}$$

with

$$\begin{aligned} b_{j}^{n+1}=i u_{j}^{n-1}-\mu \sum _{k=1}^{M}c_{j-k}^{(\alpha )}u_{k}^{n-1}-d_{j}^{n+1}u_{j}^{n-1}, \quad j=1,2,\ldots ,M, \end{aligned}$$

the first difference scheme in (2.1) can be rewritten as the following matrix vector form:

$$ A^{n+1}u^{n+1}=b^{n+1},\quad n=1,2,\ldots ,N-1, $$
(2.2)

where

$$\begin{aligned} A^{n+1}=D^{n+1}+\widetilde{T}. \end{aligned}$$

Here, \(D^{n+1}\) is a diagonal matrix defined by \(D^{n+1}=\operatorname{diag}(d_{1}^{n+1},d_{2}^{n+1},\ldots ,d_{M}^{n+1})\), and T̃ is a complex Toeplitz matrix which is just the symmetric real Toeplitz matrix T plus an imaginary identity matrix iI as follows:

$$\begin{aligned} \widetilde{T}=\mu \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} c_{0}^{(\alpha )} & c_{-1}^{(\alpha )} & \cdots & c_{2-M}^{(\alpha )} & c_{1-M} ^{(\alpha )}\\ c_{1}^{(\alpha )} & c_{0}^{(\alpha )} & c_{-1}^{(\alpha )}& \cdots & c_{2-M}^{(\alpha )} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ c_{M-2}^{(\alpha )} & c_{M-3}^{(\alpha )} & \cdots & c_{0}^{(\alpha )} & c_{-1}^{(\alpha )} \\ c_{M-1}^{(\alpha )} & c_{M-2}^{(\alpha )} & \cdots & c_{1}^{(\alpha )} & c_{0}^{(\alpha )} \end{array}\displaystyle \right ) +iI\triangleq T+iI. \end{aligned}$$
(2.3)

Because of the factors \(\gamma ,\rho >0,\beta \geq 0\), and the properties of the coefficients \(c_{k}^{(\alpha )}\), it is clear that the Toeplitz matrix T is symmetric and strictly diagonally dominant, then symmetric positive definite, and \(D^{n+1}\) is a nonnegative diagonal matrix. Thus, the matrix \(D^{n+1}+T\) is symmetric positive definite. Consequently, the coefficient matrix \(A^{n+1}\triangleq D^{n+1} +\widetilde{T}\) is a diagonal-plus-Toeplitz matrix and is symmetric and non-Hermitian positive definite.

3 Algorithms

We consider matrix splitting iteration methods for solving the following system of linear equations:

$$ Au=b,\quad A \in \mathbb{C}^{M\times M}, b\in \mathbb{C}^{M}, $$
(3.1)

where A is a complex symmetric and non-Hermitian positive definite matrix of the form \(A=D+\widetilde{T}, D \in \mathbb{R}^{M\times M}\) is a real diagonal matrix of nonnegative diagonal elements, and \(\widetilde{T}\in \mathbb{C}^{M\times M}\) is a complex symmetric Toeplitz and non-Hermitian positive definite matrix.

Splitting A with respect to its diagonal and Toeplitz parts D and T̃, for a medium-shifting, we have

$$\begin{aligned} A=M_{\omega }-N_{\omega } \end{aligned}$$

with

$$\begin{aligned} M_{\omega }=\omega I+\widetilde{T} \quad \mbox{and} \quad N_{\omega }=\omega I-D, \end{aligned}$$
(3.2)

where \(\omega =\frac{d_{\min }+d_{\max }}{2}\), \(d_{\min }\) and \(d_{\max }\) are the smallest and largest elements of the diagonal matrix D. Thus, a splitting iteration method with medium-splitting (MS) is precisely stated in the following.

Algorithm 3.1

(MS)

Given an initial guess \(u^{(0)}\), for \(k=0,1,\ldots \) , until \(\{u^{(k)}\}\) converges, compute

$$\begin{aligned} (\omega I+\widetilde{T})u^{(k+1)}=(\omega I-D)u^{(k)}+b. \end{aligned}$$
(3.3)

The iteration matrix is given by

$$\begin{aligned} G_{\omega }=(\omega I+\widetilde{T})^{-1}(\omega I-D). \end{aligned}$$
(3.4)

The following theorem demonstrates the convergence of Algorithm 3.1 under the reasonable assumptions.

Theorem 3.1

Let \(A=D+\widetilde{T}=D+T+iI \in \mathbb{C}^{M\times M}\), where \(\widetilde{T}\in \mathbb{C}^{M\times M}\) is a symmetric and non-Hermitian positive definite Toeplitz matrix, and \(D=(d_{1},d_{2},\ldots ,d_{M})\in \mathbb{R}^{M\times M}\) is a diagonal matrix with nonnegative elements. Assume that \(d_{\min }\), \(d_{\max }\) and ω are described as

$$ d_{\min }=\min_{1\leq p\leq M}\{d_{p}\},\qquad d_{\max }=\max_{1\leq p\leq M}\{d_{p}\} \quad\textit{and}\quad \omega =\frac{d_{\min }+d_{\max }}{2}, $$

then the spectral radius \(\rho (G_{\omega })\) is bounded by

$$ \delta _{\omega }=\frac{\omega -d_{\min }}{\sqrt{(\omega +\lambda _{\min })^{2}+1}}=\frac{d_{\max }-d_{\min }}{2\sqrt{(\omega +\lambda _{\min })^{2}+1}}, $$

where \(\lambda _{\min }\) is the smallest eigenvalue of T.

Moreover, it holds that \(\rho (G_{\omega })\leq \delta _{\omega } < 1\). That is to say, the MS method converges to the unique solution \(u_{*}\) of (3.1).

Proof

By the similarity invariance of the matrix spectrum as well as (3.4), we have

$$ \begin{aligned} \rho (G_{\omega }) &= \rho \bigl((\omega I+ \widetilde{T})^{-1}(\omega I-D) \bigr) \\ &= \rho \bigl((\omega I+T+iI)^{-1}(\omega I-D) \bigr) \\ &\leq \bigl\Vert (\omega I+T+iI)^{-1}(\omega I-D) \bigr\Vert _{2} \\ &\leq \bigl\Vert (\omega I+T+iI)^{-1} \bigr\Vert _{2} \Vert \omega I-D \Vert _{2} \\ & = \max_{\lambda _{i}\in \lambda (T)}\frac{1}{\sqrt{(\omega +\lambda _{i})^{2}+1}} \max_{d_{i}\in \Sigma (D)} \vert {\omega -d_{i} \vert } \\ & = \frac{\omega -d_{\min }}{\sqrt{(\omega +\lambda _{\min })^{2}+1}} \\ & = \frac{d_{\max }-d_{\min }}{2\sqrt{(\omega +\lambda _{\min })^{2}+1}}. \end{aligned} $$

The upper bound of \(\rho (G_{\omega })\) is obtained.

It is known that \(\delta _{\omega }=\frac{\omega -d_{\min }}{\sqrt{(\omega +\lambda _{\min })^{2}+1}} < 1\) is equivalent to

$$\begin{aligned} &\omega ^{2}+d_{\min }^{2}-2\omega d_{\min }< \omega ^{2}+\lambda _{\min }^{2}+2\omega \lambda _{\min }+1 \\ &\quad \Longleftrightarrow \quad \lambda _{\min }^{2}-d_{\min }^{2}+2 \omega (\lambda _{\min }+d_{\min })+1 >0 \\ &\quad \Longleftrightarrow \quad (\lambda _{\min }+d_{\min }) (\lambda _{\min }-d_{\min }+2\omega )+1 >0 \\ &\quad \Longleftrightarrow \quad (\lambda _{\min }+d_{\min }) (\lambda _{\min }+d_{\max })+1 > 0. \end{aligned}$$

It is easily obtained that \(\rho (G_{\omega })\leq \delta _{\omega }<1\) from \(\lambda _{\min }\), \(d_{\min }\) and \(d_{\max }\) are all nonnegative. Hence, the MS method converges to the unique solution \(u_{*}\) of (3.1). □

In Algorithm 3.1, the matrices \(\omega I+\widetilde{T}\) and \(\omega I-D\) are Toeplitz and diagonal matrices, respectively. In order to reduce the computing time and improve the efficiency of the MS method, we can employ the fast and superfast algorithms of the inverse of the Toeplitz matrix to solve the linear system.

The splitting iteration Algorithm 3.1 naturally induces the preconditioning matrix \(M_{\omega }^{-1}\) defined in (3.2) for the coefficient matrix \(A \in \mathbb{C}^{M\times M}\) of the linear system (3.1). We know that the Toeplitz matrix T can be approximated well by a circulant matrix. In order to further reduce the computational costs and accelerate the convergence rate of the MS iteration method, we changed equivalently the symmetric linear system (3.1) by choosing a circulant matrix, \(C\in \mathbb{C}^{M\times M}\), obtaining the preconditioned MS (PMS) iteration method. More concretely, the preconditioner is generated from Strang’s circulant preconditioner. We can take C to be Strang’s circulant approximation obtained by copying the central diagonals of T and bringing them around to complete the circulant requirement. When M is odd,

$$ C=\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} c_{0}^{(\alpha )} & c_{-1}^{(\alpha )} & \cdots & c_{\frac{M-1}{2}}^{(\alpha )} & c_{\frac{M-1}{2}}^{(\alpha )} & \cdots & c_{-1}^{(\alpha )} \\ c_{1}^{(\alpha )} & c_{0}^{(\alpha )} & \ddots & \ddots & c_{\frac{M-1}{2}}^{(\alpha )} & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & \ddots & \ddots & c_{\frac{M-1}{2}}^{(\alpha )} \\ c_{\frac{M-1}{2}}^{(\alpha )} & \ddots & \ddots & \ddots & \ddots & \ddots & c_{\frac{M-1}{2}}^{(\alpha )} \\ c_{\frac{M-1}{2}}^{(\alpha )} & c_{\frac{M-1}{2}}^{(\alpha )} & \ddots & \ddots & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & \ddots & \ddots & c_{-1}^{(\alpha )} \\ c_{1}^{(\alpha )} & \cdots & c_{\frac{M-1}{2}}^{(\alpha )} & c_{\frac{M-1}{2}}^{(\alpha )} & \cdots & c_{1}^{(\alpha )} & c_{0}^{(\alpha )} \end{array}\displaystyle \right ) , $$

when M is even, it can be treated similarly as follows:

$$ C=\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} c_{0}^{(\alpha )} & c_{-1}^{(\alpha )} & \cdots & c_{\frac{M}{2}}^{(\alpha )} & 0 & c_{\frac{M}{2}}^{(\alpha )} & \cdots & c_{-1}^{(\alpha )} \\ c_{1}^{(\alpha )} & c_{0}^{(\alpha )} & \ddots & \ddots & c_{\frac{M}{2}}^{(\alpha )} & 0 & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & c_{\frac{M}{2}}^{(\alpha )} \\ c_{\frac{M}{2}}^{(\alpha )} & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & 0 \\ 0 & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & c_{\frac{M}{2}}^{(\alpha )} \\ c_{\frac{M}{2}}^{(\alpha )} & 0 & \ddots & \ddots & \ddots & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & \ddots & 0 & \ddots & c_{-1}^{(\alpha )} \\ c_{1}^{(\alpha )} & \cdots & c_{\frac{M}{2}}^{(\alpha )} & 0 & c_{\frac{M}{2}}^{(\alpha )}& \cdots & c_{1}^{(\alpha )} & c_{0}^{(\alpha )} \end{array}\displaystyle \right ) . $$

According to the property of the coefficients \(c_{k}^{(\alpha )}, k=0, 1, \ldots , M-1\), we see that C is symmetric and strictly diagonally dominant, resulting in it being symmetric positive definite.

Algorithm 3.2

(PMS)

Given an initial guess \(u^{(0)}\), for \(k=0,1,\ldots \) , until \(\{u^{(k)}\}\) converges, compute

$$\begin{aligned} (\omega I+C+iI)u^{(k+1)}=(\omega I-D+C-T)u^{(k)}+b, \end{aligned}$$
(3.5)

here \(\omega =\frac{d_{\min }+d_{\max }}{2}\) is the medium of \(d_{\min }\) and \(d_{\max }\), where \(d_{\min }\) and \(d_{\max }\) are the minimum and maximum elements of the diagonal matrix D.

Remark 3.1

In Algorithm 3.2, the matrix \(\omega I+C+iI\) is circulant, we can complete effectively via fast and superfast algorithms. In fact, scheme (3.5) can be regarded as a standard stationary iteration method as follows:

$$\begin{aligned} \widetilde{M}_{\omega }u^{(k+1)}= \widetilde{N}_{\omega }u^{(k)}+b, \end{aligned}$$
(3.6)

where \(\widetilde{M}_{\omega }=\omega I+C+iI\) and \(\widetilde{N}_{\omega }=\omega I-D+C-T\). Hence, \(\widetilde{M}_{\omega }^{-1}\) can be considered as a preconditioner of (3.1). We have naturally

$$\begin{aligned} \bigl\Vert \widetilde{M}_{\omega }^{-1}A \bigr\Vert _{2} =& \bigl\Vert (\omega I+C+iI)^{-1}A \bigr\Vert _{2} \\ \leq &\bigl\Vert (\omega I+C+iI)^{-1} \bigr\Vert _{2}\cdot \Vert A \Vert _{2} \\ =&\max_{\nu _{p}\in \lambda (C)}\frac{1}{\sqrt{(\omega +\nu _{p})^{2}+1}}\cdot \Vert A \Vert _{2} \\ =&\frac{1}{\sqrt{(\omega +\nu _{\min })^{2}+1}}\cdot \Vert A \Vert _{2} \\ =&\kappa \cdot \Vert A \Vert _{2}, \end{aligned}$$

where \(\kappa =\frac{1}{\sqrt{(\omega +\nu _{\min })^{2}+1}}<1\). Therefore, the eigenvalues distribution of the matrix \(\widetilde{M}_{\omega }^{-1}A\) is tighter than that of the matrix A by rough estimate. It is verified by numerical experiments in the next section.

Remark 3.2

Because the circulant preconditioner is the approximation of the Toeplitz matrix, the proof of the convergence property for the PMS iteration method is similar to the MS iteration method. Therefore, we will not repeat the proof process of the convergence property in Algorithm 3.2 here.

4 Numerical experiments

In this section, two numerical examples to assess the feasibility and effectiveness of Algorithms 3.1–3.2 in terms of iteration number (denoted by “IT”), computing time (in seconds, denoted by “CPU”), and the relative error (denoted as “Error”) are provided. All our tests are started from zero vector \(u^{(0)}\) and terminated once either the maximal number of iteration steps is over 10,000 (denoted as “–”) or the current iterate satisfies

$$ \mbox{Error}=\frac{\Vert b-Au^{(k)} \Vert _{2}^{2}}{\Vert b \Vert _{2}^{2}}< 10^{-6}. $$

In addition, all the experiments are carried out using MATLAB (version R2013a) on a personal computer with 2.4 GHz central processing unit (Intel® CoreTM 2 Quad CPU), 4.00 GB memory and Windows 7 operating system.

Example 1

Let \(\gamma =1, \rho =2, \beta =0, 1<\alpha <2\). Then system (1.1) is decoupled and becomes

$$ i\frac{\partial u(x,t)}{\partial t}+ (-\Delta )^{\frac{\alpha }{2}}u(x,t)+2\vert u \vert ^{2}u(x,t) = 0 , \quad (x,t)\in [-20,20]\times (0,2] $$

subjected to the initial boundary value conditions

$$ u(x,0)=\operatorname{sech}(x)\cdot \exp(2ix), \qquad u(-20,t)=u(20,t)=0. $$

Here and in the sequel, the direct methods can be used to solve the linear systems (3.3) and (3.5), named MS1 and PMS1 methods, respectively. Correspondingly, we employ the fast Zohar algorithm and the fast Fourier transform (FFT) to solve the linear systems (3.3) and (3.5), named MS2 and PMS2 methods, respectively.

In Tables 1–2, we report the number of iteration steps, the computing time, and the relative error of the methods used in the experiments for Example 1 when \(\alpha =1.2\) and \(\alpha =1.4\) with respect to different spatial grids. The time step sizes for all numerical experiments are set to be 0.05.

Table 1 Numerical results of the Example 1 for \(\alpha=1.2\)
Full size table
Table 2 Numerical results of the Example 1 for \(\alpha=1.4\)
Full size table

From Tables 1–2, we see that the iteration steps of PMS2, PMS1, MS2, and MS1 methods are pretty stable and always kept in 3 with the growth of the number of spatial grid points, but those of the SOR iteration method are increasing quickly. As for the computing time, that of the PMS2 method is the least of all methods in the experiments, while the time of the SOR method has already reached over 1000 seconds when \(M=10\text{,}000\). Figure 1, which depicts the comparison of resulting CPU of PMS2, MS2, and SOR iteration methods for Example 1, intuitively shows that the PMS2 method performs pretty well.

Figure 1
figure 1

Comparison of the resulting CPU of these algorithms in Example 1

Full size image

Example 2

Let \(\gamma =1\), \(\rho =2\), \(\beta =1\), \(1<\alpha <2\), then we have the following coupled system:

$$ \textstyle\begin{cases} i\frac{\partial u(x,t)}{\partial t}+ (-\Delta )^{\frac{\alpha }{2}}u(x,t)+2(\vert u \vert ^{2}+\vert v \vert ^{2})u(x,t) = 0 , \\ i\frac{\partial v(x,t)}{\partial t}+ (-\Delta )^{\frac{\alpha }{2}}v(x,t)+2 (\vert v \vert ^{2}+ \vert u \vert ^{2})v(x,t) = 0. \end{cases}\displaystyle (x,t)\in [-20,20]\times (0,2]. $$

We take the initial boundary value conditions in the form

$$ \textstyle\begin{cases} u(x,0)=\operatorname{sech}(x+1)\cdot \exp(2ix),\qquad v(x,0)=\operatorname{sech}(x-1)\cdot \exp(-2ix), \\ u(-20,t)=u(20,t)=0,\qquad v(-20,0)=v(20,t)=0. \end{cases} $$

In Tables 3–4, we list the number of iteration steps, the computing time, and the relative error of the methods used in the experiments for Example 2 when \(\alpha =1.2\) and \(\alpha =1.4\) with respect to different spatial grids. The time step sizes for all numerical experiments are also set to be 0.05.

Table 3 Numerical results of the Example 2 for \(\alpha=1.2\)
Full size table
Table 4 Numerical results of the Example 2 for \(\alpha=1.4\)
Full size table

Tables 3–4 show that the iteration steps of PMS2 and MS2 methods are constant no matter what the number of the spatial grid points is, but those of the SOR iteration method are increasing quickly. The PMS2 and MS2 methods require less computing time than the SOR iteration method. The advantage of the computing time of the PMS2 method over the other methods for different values of α and M can be visually shown in Fig. 2.

Figure 2
figure 2

Comparison of the resulting CPU of these algorithms in Example 2

Full size image

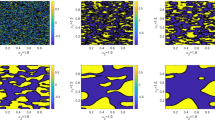
We also exhibit the preferable numerical behavior for Example 1 in terms of the eigenvalues of \(\widetilde{M}_{\omega }^{-1}A\). We can see that the eigenvalues of \(\widetilde{M}_{\omega }^{-1}A\) are tighter than those of A by sketching the circles in Figs. 3–6, whose centers are all the middle points of the smallest and largest eigenvalues of the preconditioner \(\widetilde{M}_{\omega }^{-1}\), and their radii are half of the distance between the two points.

Figure 3
figure 3

The eigenvalues of the matrices A (left) and \(\widetilde{M}_{\omega }^{-1}A\) (right) when \(\alpha =1.2\) and \(M=800\)

Full size image
Figure 4
figure 4

The eigenvalues of the matrices A (left) and \(\widetilde{M}_{\omega }^{-1}A\) (right) when \(\alpha =1.2\) and \(M=1600\)

Full size image
Figure 5
figure 5

The eigenvalues of the matrices A (left) and \(\widetilde{M}_{\omega }^{-1}A\) (right) when \(\alpha =1.4\) and \(M=800\)

Full size image
Figure 6
figure 6

The eigenvalues of the matrices A (left) and \(\widetilde{M}_{\omega }^{-1}A\) (right) when \(\alpha =1.4\) and \(M=1600\)

Full size image

5 Conclusion

According to the discretization of the spatial fractional coupled nonlinear Schrödinger equations, we have obtained that the coefficient matrix is the sum of a real diagonal matrix D and a complex symmetric Toeplitz matrix T̃, which is just the symmetric real Toeplitz T plus an imaginary identity matrix iI, and then established a new splitting iteration method with medium-shifting (MS). Since the structure of the coefficient matrix is Toeplitz matrix, the iteration method with medium-shifting sufficiently employs the fast and superfast direct methods of complexity \(\mathcal{O}(M^{2})\) and \(\mathcal{O}(M\log^{2}M)\), respectively. Furthermore, we replace the Toeplitz matrix T by an appropriate circulant matrix C and obtain the preconditioned MS (PMS) iteration method. In terms of the special structure of coefficient matrix in Algorithms 3.1–3.2, we need to solve the linear system associated with the shifted Toeplitz matrix and the shifted circulant matrix, respectively, by employing fast and superfast algorithms. Theoretical analysis shows that the approach is convergent, and numerical experiments have already demonstrated its efficiency.