Blockchain-IoT peer device storage optimization using an advanced time-variant multi-objective particle swarm optimization algorithm

Abstract

The integration of Internet of Things devices onto the Blockchain implies an increase in the transactions that occur on the Blockchain, thus increasing the storage requirements. A solution approach is to leverage cloud resources for storing blocks within the chain. The paper, therefore, proposes two solutions to this problem. The first being an improved hybrid architecture design which uses containerization to create a side chain on a fog node for the devices connected to it and an Advanced Time-variant Multi-objective Particle Swarm Optimization Algorithm (AT-MOPSO) for determining the optimal number of blocks that should be transferred to the cloud for storage. This algorithm uses time-variant weights for the velocity of the particle swarm optimization and the non-dominated sorting and mutation schemes from NSGA-III. The proposed algorithm was compared with results from the original MOPSO algorithm, the Strength Pareto Evolutionary Algorithm (SPEA-II), and the Pareto Envelope-based Selection Algorithm with region-based selection (PESA-II), and NSGA-III. The proposed AT-MOPSO showed better results than the aforementioned MOPSO algorithms in cloud storage cost and query probability optimization. Importantly, AT-MOPSO achieved 52% energy efficiency compared to NSGA-III. To show how this algorithm can be applied to a real-world Blockchain system, the BISS industrial Blockchain architecture was adapted and modified to show how the AT-MOPSO can be used with existing Blockchain systems and the benefits it provides.

Introduction

Blockchain has gained tremendous traction over the past decade due to its remarkable contribution to cryptocurrency. The emergence of Blockchain as a distributed ledger technology led to its application in areas such as healthcare [1, 2], supply chain management [3], education [4], real estate [5] as well as Internet of Things (IoT) [6].

Blockchain varies from centralized digital databases and ledgers because it harnesses the concept of community validation to synchronize the entries that go into the ledger. It further works via a distributed model to replicate the updated ledger to all the nodes and users involved in the network [7]. Blockchain is a very robust technology due to its decentralized, transparent, secure, immutable and automated characteristics. However, many researchers have highlighted scalability as a crucial concern affecting Blockchains and this needs critical attention [8]. The scalability setback, which includes low throughput, resource-intensive computations, and high latency, has dramatically hindered practical Blockchain-based applications.

Another critical concern that affects Blockchain adoption is the storage space requirements needed to run a Blockchain node. The space requirement is a Blockchain component that increases daily due to the Blockchain ledger's append-only nature [9]. The more transactions completed, the larger the ledger size. According to a study by Statista [10], it was reported that the Blockchain size of Bitcoin as of February 2021 stood at 321.32 GB, and it will take a new full node, a bootstrap time of roughly four days, to be a part of the network. Ethereum [11], which is also another popular Blockchain, suffers from a similar situation.

Several solutions have been proposed to handle the issue of scalability on Blockchains. Some of these solutions include sharding (on-chain scaling) [12], state channels (off-chain scaling), side chains with schemes as Plasma [13] for the Ethereum network, the bloXroute technology [14] as well as Directed Acyclic Graph (DAG) [15].

These outlined issues about Blockchains become even more profound when IoTs are integrated into Blockchains. IoT solutions require that many transactions be executed at every given time [16], but some Blockchain networks such as Bitcoin can only be capable of performing 7–20 transactions per second [8]. IoT devices are limited when it comes to the aspects of their storage and computational resources. On the other hand, rapid improvement in computing technologies has led to the development of concepts and systems such as Edge computing [17]. Edge computing is an extension of cloud computing [18], because it enables many devices to run applications at the edge of a network. It is done by providing compute resources for devices to offload tasks that are computationally intensive and provide data storage, maintain low latency, support heterogeneity and improve the quality of service for applications that require low latency, such as IoT applications [17]. Edge computing has been partly used to solve the scalability for Blockchain-IoT (BIoT) applications such that the IoT devices do not act as nodes on the Blockchain. Instead, they connect to these edge computers instead of nodes on the Blockchain [19]. These edge/fog computing structures tend to have more computational and storage resources, but the number of transactions produced by these IoT devices still puts considerable pressure on them.

Some existing solutions [20] to this storage problem mainly include storing some of the blocks produced by these edge nodes in the cloud. Most of the proposed solutions based on this have been backed by the fact that there has been significant improvement in the security and encryption schemes implemented on cloud platforms. To the best of our knowledge, not much literature exists which addresses the cloud storage problem by using optimization techniques. Xu et al. [21] formulated this problem into a multi-objective block selection problem and solved it using a Non-dominated Sorting Genetic Algorithm with Clustering (NSGA-C). Their approach had a few limitations, which this paper seeks to improve. First of all, when compared to NSGA-III, NSGA-C performed worse in 4 out of 5 objective functions and only out performed NSGA-III in the last objective function. Secondly, the NSGA-III has a quite long runtime and NSGA-C has an even longer runtime. This is not quite ideal because for just three peers the block selection algorithm took upwards of 10 min to run. This also means that the energy consumed during the running of this algorithm was also increased. When conducting this research, we set out with the quest to have an optimization scheme that performed better for all objective functions and also run in less than the current NSGA-C algorithm. In our investigations, we also realized that no research had been performed where MOPSO had been applied to this problem, thus, we propose this novel Advanced Time-Variant Multi-Objective Particle Swarm Optimization (AT-MOPSO).

The paper aims to take advantage of the improvements made in cloud technologies and leverage the colossal storage availability on cloud systems to solve the storage problems faced by IoT nodes. We seek to accomplish this by storing some blocks in the cloud and maintaining the Blockchain's decentralized nature by leveraging different cloud providers and cloud deployment strategies such as containerization. The paper adapts our improved hybrid IoT architecture design [22] to show how our Advanced Time-Variant Multi-Objective Particle Swarm Optimization (AT-MOPSO) algorithm would help solve the block selection cloud storage problem. We also applied it to the BISS architecture [23] from one of our recent research works to improve it and further show how legacy machines with limited capabilities can be brought closer to the Blockchain as nodes. The main contributions of the paper are:

• 1. Proposing a framework to ensure improved operation for fog/edge nodes by leveraging the power of side-chains and containers based on an improved hybrid architecture design in [22].

• 2. Formulating the problem into an optimization scheme for cloud providers' storage cost, the query probabilities of blocks on IoT fog peers, and storage availability on IoT fog nodes.

• 3. Proposing an Advanced Time-variant Multi-Objective Particle Swarm Optimization (AT-MOPSO) Algorithm to obtain the correct number of blocks to be selected from the fog nodes for cloud storage.

• 4. Comparing the energy efficiency of some Multi-Objective optimization schemes against our proposed algorithm to show our scheme's energy-saving and efficient nature.

• 5. Incorporating our scheme into an industrial Blockchain Architecture to show our scheme can be used in a real-world scenario.

Our study primarily focuses on how the storage space on Blockchain peers be optimized by sending some of the stored blocks to a cloud storage and does not deal directly with aspects of the network or the actual connection between devices.

The rest of this paper is organized as follows. Section 2 presents an overview of Blockchain, edge computing, and multi-objective optimization techniques. Section 3 looks at the proposed improvement to fog nodes and the mathematical formulation of the multi-objective block selection problem. Section 4 outlines the details of our proposed Advanced Time-Variant Multi-Objective Particle Swarm Optimization (AT-MOPSO) algorithm and the results of our scheme in comparison to other multi-objective optimization scheme is shown in Sect. 5 for all objective functions as well as the energy-saving benefits. Section 6 shows a real world application of the AT-MOPSO algorithm and Sect. 7 concludes the paper and provides recommendations for future work.

Related work

Blockchain

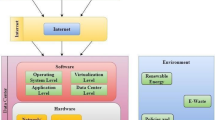
To better understand the structure and nature of Blockchain systems, it is good to look at the decomposed layers of Blockchains, as shown in Fig. 1. The figure consists of the data, network consensus, ledger topology, and contract and application layers [20].

Fig. 1

The decomposition of the structure of Blockchain

The data layer performs the function of data encapsulation so that the data generated from a Blockchain application or transaction is verified and hidden in a block. Such a block is linked to the previous block by its header with a hash value. The process results in an ordered chain of blocks replicated among all nodes on the Blockchain [12]. The replication process occurs in the network layer, whereby the generated blocks are propagated to all nodes in the Blockchain [24]. Since the Blockchain is seen as a decentralized network of nodes, it is modeled as a P2P network where peers act as participants and provide storage for the distributed ledger of blocks.

Consensus algorithms and schemes help maintain the integrity of the data on the Blockchain. The nodes on the Blockchain verify each propagated data block and ensure that it is a valid block before added to all the ledgers on all nodes. The three primary consensus schemes that have seen widespread usage include Proof-of-Work (PoW) [10], Proof-of-Stake (PoS) [25, 26], and Practical Byzantine Fault Tolerance (PBFT) [27].

The last decade has also seen an increase in the research and development of cloud-based architectures and technology. The high availability of computing resources, storage, and highly reliable and performance network infrastructure has led to more applications being run on the cloud [28]. The trend also led to a second wave that seeks to move these highly performance systems from the cloud to the edge of networks [20]. The shift to the edge is mainly being done to support applications that require little to no delay in their operations. Such applications include IoT implementations [17, 29] and Virtual Reality applications [30], etc. The adoption of edge/fog computing to support Blockchain and IoT applications' integration is due to the resource limitations on IoT devices and the low latency communication usually required in their operations.

We realized that much work had not been done concerning the ledger topology layer of the Blockchain system from the research that we have conducted. This is essential because this layer is required to store the authenticated blocks produced from the consensus layer. Large storage capacities are needed for this. The issue is very profound when Blockchain-IoT integrations and applications are considered, mainly because of the storage limitations on these IoT devices. Fog Computing structures used for IoT implementations take a lot of this load off IoT devices, but the large amounts of data produced by the IoT devices can still put high demands on these fog nodes.

Palai et al. [31] proposed an approach where a block would summarize the transactions of several consecutive blocks. Then this summary block would be used to make a net change on those blocks, thereby reducing the storage footprint. The only problem with this approach is that if only a few blocks are summarized, then the summary blocks' size is not any smaller than a set of continuous blocks. The authors in [32] also proposed architecture to solve Blockchains' storage problems using a class of erasure codes known as 'Fountain codes'. This architecture enables a full node on the Blockchain to encode blocks that other nodes have validated into a more compressed structure made up of different blocks, reducing the storage space needed.

Yang et al. [33] proposed a dual storage solution that uses both an on-chain and off-chain approach. Their approach was used for a fruit and vegetable traceability application with IoT devices serving as input devices. The public information about products was stored in a relational database, and the private information about the products was sent over to the Blockchain. This approach is also efficient since fewer data would be sent over to the Blockchain. The downside of such an approach is that if there is data loss on the side relational database, that data cannot be retrieved, and the private information sent to the Blockchain would be without context.

Kumari et al. [34] also proposed an off-chain approach intended for use in an innovative city application for IoT devices acting as smart meters and sensors. The off-chain solution uses the InterPlanetary File System (IPFS) [34], a peer-to-peer hypermedia protocol to store only transactions related to the devices off-chain and links the off-chain records to the main Ethereum Blockchain, thereby reducing storage requirements and costs.

Containerization

Another trend that has caught on with the popularization of cloud and edge/fog computing is the concept of containers. Fog computing, which is known to solve the latency issue for IoT devices, works by deploying a set of distributed servers and compute resources at the edge of the network. The infrastructure helps avoid data transmission over long distances, thus avoiding propagation and processing delays [29]. Complex configurations and different software environments have to be set up on fog servers to fulfill the demands of various applications' needs. Containerization has been used in such cases to help solve the problem of software deployment and configurations and migration activities [19]. The process is achieved by bundling all the relevant source codes with their respective library requirements into encapsulations known as containers which can be easily deployed on the fog servers.

Some researchers have proposed systems to use containerization orchestrations with Blockchain and IoT applications, but not much literature exists on this topic. Cui et al. [6] proposed a Blockchain-based containerization scheme for an aspect of IoTs known as the Internet of Vehicles (IoV). Their implementations focused on the container scheduling policies for Directed Acyclic Graphs (DAGs), which determined how many containers should be running to effectively manage the resources on the fog servers that the vehicles were utilizing. In [35], the authors proposed a Blockchain system based on Distributed Hash Table (DHT) called LightChain. The Blockchain implementation was deployed on a single machine using a docker container, and this was done to show its lightweight nature. The individual nodes of the Blockchain were run as separate threads in the container.

Multi-objective optimization

Multi-objective optimization is defined as the process of obtaining a suitable vector of variables from a feasible region that a set of constraints can defines. The goal is to find the vector of variables such that a vector of objective functions would be minimized or maximized. It can be expressed as follows:

$$\min F\left( x \right) = \left\{ {f1\left( x \right), f2\left( x \right), \ldots , fm\left( x \right)} \right\},\,\,\,\,{\text{s.t}}.\,\,\,\, g\left( x \right) \le 0$$

(1)

In this case, $x$ represents the vector of design variables—each value of $f_{i}$, for $i\left( {1 \le i \le m} \right)$ representing an objective function that must be optimized and $g\left( x \right)$ is the constraint vector with m being the number of objective functions in question.

Evolutionary algorithms have been used widely in research to solve multi-objective problems, and the general term used for these is Multi-Objective Evolutionary Algorithms (MOEA) [36]. Such algorithms possess parallel efficiency, robustness, and versatility when applied to complex optimization scenarios. Ridha et al. [37] used multi-objective optimization to solve the problem of standalone photovoltaic system design. Their research aimed to optimize the output power obtained from a given system using storage battery capacity, mathematical models of the different types of PV modules, and environmental criteria. Cai et al. [24] also proposed a sharding scheme based on multi-objective optimization. The scheme presented an optimized shard validation model, which improved the throughput of the Blockchain network and reduced the aggregation of malicious nodes in the assigned shards.

Not much research exists where multi-objective optimization has been used to solve the block storage problem for IoT devices. Xu et al. [21] proposed an algorithm based on a Non-dominated Sorting Genetic Algorithm (NSGA-III) with K-Means clustering to obtain a crowding distance that helps to select the Pareto optimal solution from the set of generated keys. They modeled the factors needed to choose the appropriate number of blocks to be sent to the cloud. These include the local space occupancy of the IoT, query probabilities of the peers (IoT devices), and the cloud's storage cost.

In this paper, we propose an Advanced Time-variant Multi-Objective Particle Swarm Optimization Algorithm (AT-MOPSO), which is based on the Multi-Objective Particle Swarm Optimization (MOPSO) [38] algorithm. MOPSO is a variant of Particle Swarm Optimization (PSO) for solving multi-objective optimization problems. Both PSO and MOPSO have a defect: they can get stuck in the local optimal solution space in the search process for the optimal global solution. The AT-MOPSO seeks to solve the MOPSO algorithm's defects and provide results for the optimal number of blocks that should be sent to the cloud for each IoT device.

System model and problem statement

System model

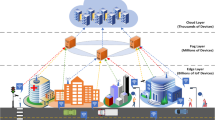
In this paper, we propose a system for fog servers specifically for Blockchain-IoT applications such that a side-chain would be run on the fog server, and the nodes of the side-chain would be individual containers. Each of these containers would serve an IoT device and offload all Blockchain-related activities from the device. The fog node would itself serve as a full node on the main Blockchain.

In our proposed IoT-Fog node architecture in Fig. 2, the Fog computing node would not just be a node connected to the Blockchain. The Fog node would instead run a side chain for the devices that are connected to it. In such a case, completed transactions on the side chain will be sent to the main chain. The Blockchain mining process and interactions are still going to be abstracted from the IoT peer devices. The fog will not employ a traditional service-oriented monolithic architecture [39], and the nodes of the Blockchain would not be the IoT peer devices. The way the side chain would operate would be by using microservices [6]. Thus, multiple microservices would run as containers on the fog that would act as nodes on the side-chain. These containers would take up the mining activities from the IoT devices.

Fig. 2

Proposed system for running a side chain on a fog node using containers and microservice

Each IoT device would be randomly assigned to a Node in the side-chain (i.e., a container). Separate containers would not be created for each IoT device, but rather a pool of IoT devices would be assigned to a node at a time. The depiction of this proposed update is shown in Fig. 2.

Only a limited amount of delay is introduced for message propagation through the side-chain, ensuring high throughput of transactions resulting from the small number of container nodes. This architecture would be best suited for the high transaction—high-performance IoT implementations.

As mentioned earlier, the Blockchain's storage requirements on the fog node are quite intensive because even a low throughput Blockchain such as Bitcoin has a ledger size of about 321.21 GB. In contrast, a high throughput Blockchain such as Ripple has a ledger size of up to 9TB [32]. Our proposed system curtails this challenge by moving blocks from fog nodes to the cloud for storage, as shown in Fig. 2.

Problem statement

Based on our proposed model, the question that arises is which blocks should be moved to the cloud and how many of those blocks should be moved to ensure the smooth and efficient running of the IoT devices connected to it. This problem is formulated with the appropriate mathematical models are presented here in this section of the paper.

Suppose we have several fog servers acting as fog nodes or peers for IoT devices connected to it as $S=\left\{{s}_{1}, {s}_{2}, \dots , {s}_{m}\right\}$, where ${s}_{i}\in S$ denotes a single server and $m$ the total number of fog nodes being considered. For each fog node/peer, we need to select some blocks to be sent to the cloud to alleviate that peer's storage pressure. The blocks in each fog node can be represented by $b_{1} , b_{2} , \ldots , b_{N}$, where $N$ is the number of blocks mined by the peer at any given time.

The number of blocks that would be taken to the cloud can be represented by $M_{{\text{w}}} \left( {1 \le M_{{\text{w}}} \le N} \right)$, where $w = s_{i} \in S$ as shown in Fig. 3.

Fig. 3

A representation of the blocks present in a fog node where Mw blocks would be transferred

Once ${M}_{w}$ blocks are sent to the cloud the blocks in the fog peer are renumbered such that $b_{{M_{{\text{w}}} + 1}}$ then becomes $b_{1}$ and so on.

Based on the type of application that the Blockchain-IoT implementation is being used to serve, we can have three different query conditions for the blocks on the fog node. The query conditions can be for either a fixed case or linear decay scenarios. The fixed case scenario when used in a traceability application such as [33] denoted in (2). The linear decay scenario describes when the blocks are not queried as often as denoted by (3). In exponential decay scenarios, the Blockchain is used as storage for transactions such as in cryptocurrencies, as denoted by (4).

$$F\left( t \right) = F_{0}$$

(2)

$$F\left( t \right) = F_{0} - \alpha_{2} t.$$

(3)

$$F\left( t \right) = F_{0} e^{{ - \alpha_{1} t}}$$

(4)

where $\alpha_{1}$ represents the attenuation coefficient in the exponential decay scenario, and $\alpha_{2}$ represents that for the linear decay scenario. These can be determined based on the Blockchain use case scenario.

Xu et al. [21] proposed that the number of blocks taken to the cloud for each peer on a Blockchain can be formulated into a multi-objective optimization problem based on three main objective functions. These are the Query Probability of the various blocks on the fog node. The cloud storage cost when some blocks are moved to the cloud, and the local space occupancy represents that amount of local space on the fog node that will be alleviated by sending some of the blocks to the cloud. The mathematical models for these objective functions are outlined as follows:

Query probability

The query probability for the blocks in a fog node is based on the query frequency $F\left( t \right)$ for the type of Blockchain-IoT application being implemented. The value represented as t for every block is tightly coupled to when that block was generated. Thus, with the addition of every new block, $t$ is increased by 1. This means that the first generated block in the set has a t value of 0 as shown in (5). In the eventual scheme of events, the first generated block would be the last block in the arrangement given by $b_{N}$ as shown in Fig. 3.

$$\Rightarrow t = 0, F\left( t \right) = F_{0} .$$

(5)

The query probability for the blocks in a fog node can be represented by $P_{{b_{1} }} , P_{{b_{2} }} , P_{{b_{2} }} , \ldots , P_{{M_{{\text{w}}} }} , \ldots P_{{b_{{\text{N}}} }}$ where $b_{j} \left( {1 \le j \le N - 1} \right)$. Thus, the query probability for the various blocks can be found by (6). It must be noted the block $b_{{\text{N}}}$ would have both the query frequency and query probability of $F_{0}$ since it was the first block created.

$$P_{{b_{j} }} = \left\{ {\begin{array}{*{20}l} {\left[ {\frac{1}{{\mathop \smallint \nolimits_{0}^{N - j} F\left( t \right){\text{d}}t}}} \right]} \hfill & {\quad 1 \le j \le N - 1} \hfill \\ {F_{0} } \hfill & {\quad j = N} \hfill \\ \end{array} } \right..$$

(6)

Based on (6), we can calculate the sum of the all the query probability for all the blocks for a fog node as $\Lambda$ as shown in (7). The sum can be used to normalize the values of the query probabilities represented by $P_{{b_{1} }}^{\prime } , P_{{b_{2} }}^{\prime } , P_{{b_{2} }}^{\prime } , \ldots , P_{{M_{w} }}^{\prime } , \ldots , P_{{b_{N} }}^{\prime }$ as shown in (8).

$$\Lambda = \mathop \sum \limits_{j = 1}^{N - j} P_{{b_{j} }} + F_{0} .$$

(7)

$$P_{{b_{j} }}^{\prime } = \left\{ {\begin{array}{*{20}l} {\left[ {\frac{1}{{{\Lambda }\mathop \smallint \nolimits_{0}^{N - j} F\left( t \right){\text{d}}t}}} \right]} \hfill & {\quad 1 \le j \le N - 1} \hfill \\ {\frac{{F_{0} }}{{\Lambda }} } \hfill & {\quad j = N} \hfill \\ \end{array} } \right..$$

(8)

Thus, after all the query probabilities of the blocks have been found, the overall query probability for the fog node is based on the number of blocks $M_{{\text{w}}}$ to be sent to the cloud can be found. This can be achieved by finding the sum of all the normalized query probabilities up to the $M_{{\text{w}}} {\text{th}}$ block. For fog node $s_{i}$, the overall query probability is denoted by $P_{{s_{i} }}$ as shown in (9).

$$P_{{s_{i} }} = \mathop \sum \limits_{j = 1}^{{M_{w} }} P_{{b_{j} }}^{\prime } \quad 1 \le s_{i} \le m.$$

(9)

where $w = s_{i} \,\,\,{\text{and}}\,\,m = \left| S \right|$.

Based on the value of $m$, there will $m$ objective functions; one for each fog node $s_{i}$ with $P_{{s_{i} }}$ being minimized.

Storage cost

The storage cost deals with the cost of storing the blocks in the cloud. The storage cost for cloud storage is assumed to be the same for all the fog nodes for the sake of simplicity. The size of one block for each fog node is represented by $C$. Different Blockchain has different sizes for the blocks that are generated. Thus, the Blockchain being used must be considered, and the block size of an individual block must be known. For example, the bitcoin Blockchain is known to have blocks with a size of 1 MB [40], the size of blocks on the Hyperledger Fabric Blockchain can be adjusted to be as large as possible [41]. The size of a block on the Ethereum Blockchain varies based on the gas limit [11].

The storage cost is considered a linear function as shown in (10), which is the total size of all blocks moving from the fog node to the cloud. This linear function is governed by a factor $k$ representing the ratio of the cost of cloud storage compared to local storage. Thus, when $k$ has a small value, it means that cloud storage is cheaper than local storage options for the fog node and vice versa. This value is based on the cloud service provider used by a fog node and the type of local storage available on the fog node, such as Optical Hard Disk Drives (HDD)—which are slightly cheap but slow, or Solid-State Drives (SSD)—which are relatively more expensive and faster.

$$cost = kC \times \mathop \sum \limits_{w = 1}^{m} M_{{\text{w}}} .$$

(10)

where $m = \left| S \right|$.

Local space occupancy/storage availability of IoT Fog node

Local space occupancy/the storage availability of IoT Fog nodes is directly related to the number of stored blocks in the cloud. This is because the more blocks stored in the cloud, the more space would be made available on the fog node, thereby easing the given node's storage pressure. The local space occupancy is inversely proportional to the storage availability of a node. More blocks sent over to the cloud for storage means local storage occupancy would be small, and thus there would be an increase in the storage available on the IoT fog node. It should be noted that the storage size on each fog node is determined by the number of IoT devices connected to it, the type of application that it is being used for, and the operator of that fog node. Thus, some nodes may prioritize local space occupancy/storage availability more than others. In this sense, weights can be assigned to each fog node such that nodes that prioritize storage availability and have low storage capacity would be given bigger weights. The weights can be represented as $\beta_{{s_{i} }} , { }$ such that $\beta_{{s_{1} }} , { }\beta_{{s_{2} }} , { }\beta_{{s_{3} }} , \ldots , { }\beta_{{s_{m} }}$ represent weights for individual fog node where $m = \left| S \right|$. The weights would be used in a weighted sum equation to find the overall local space occupancy for the fog nodes; thus, they would be given decimal values which would sum up to 1 as shown in (11).

$$\mathop \sum \limits_{i = 1}^{m} \beta_{{s_{i} }} { } = 1 \left( {1 \le i \le m} \right).$$

(11)

The individual local space occupancy for each fog node can be denoted by $Q_{{s_{i} }}$, expressed in (12). This value is based on the number of $M_{{\text{w}}}$ blocks that are sent to the cloud. The overall local space occupancy, $Q$, of all fog nodes can be expressed as a weighted sum based on their assigned weights $\beta_{{s_{i} }}$ as shown in (13).

$$Q_{{s_{i} }} = \frac{{e^{{\left( {\frac{{N - M_{w} }}{N}} \right)}} }}{e - 1}.$$

(12)

$$Q = \mathop \sum \limits_{i = 1}^{m} Q_{{s_{i} }} \times \beta_{{s_{i} }} .$$

(13)

Multi-objective formulation

Based on the objective functions expressed earlier in the query probability, the storage cost, and the local space occupancy, the block selection problem can be formulated as a minimization multi-objective problem. This work's primary goal is to minimize the objective functions while taking as many blocks as possible to be stored in the cloud. Thus, all objective functions would be minimized, as shown in (14)–(16).

$$\begin{aligned} \min \left( {query\,probs.} \right)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\cdot}$}}{ \Rightarrow } & \min \mathop \sum \limits_{j = 1}^{{M_{{s_{1} }} }} P_{{b_{j} }}^{\prime } \\ & \min \mathop \sum \limits_{j = 1}^{{M_{{s_{i} }} }} P_{{b_{j} }}^{\prime } \\ & \min \mathop \sum \limits_{j = 1}^{{M_{{s_{m} }} }} P_{{b_{j} }}^{\prime } . \\ \end{aligned}$$

(14)

From (14), it can be seen that there will be $m$ fog nodes and thus $m$ objective functions for the query probabilities, i.e., one for each fog node. The objective functions for the storage cost and the local space occupancy also minimized, as shown in (15) and (16).

$$\min kC \times \mathop \sum \limits_{w = 1}^{m} M_{{\text{w}}} .$$

(15)

$$\min \mathop \sum \limits_{i = 1}^{m} Q_{{s_{i} }} \times \beta_{{s_{i} }} .$$

(16)

$$1 \le M_{w} \le N,\,\,\, M_{w } \in {\mathbb{N}}.$$

(17)

Thus, for every set of $m$ fog nodes that we have, it can be noted there would always be $m + 2$ objective functions that we have to adhere to at every time. Users and operators of the Blockchain-IoT applications can always have constraints on these objective functions and the individual variables used in them. The constraints can be represented with $\gamma_{1} , \gamma_{2} , \ldots , \gamma_{m + 2}$ as shown in (18). The constraints are solely the decision of the operator or the user. It must also be noted that the number of blocks that can be taken to the cloud must

$$\begin{aligned} & \max \left( {\min \mathop \sum \limits_{j = 1}^{{M_{{s_{1} }} }} P_{{b_{j} }}^{\prime } } \right) \le \gamma_{1} \\ & \max \left( {\min \mathop \sum \limits_{j = 1}^{{M_{{s_{m} }} }} P_{{b_{j} }}^{\prime } } \right) \le \gamma_{m} \\ & \max \left( {\min kC \times \mathop \sum \limits_{w = 1}^{m} M_{w} } \right) \le \gamma_{m + 1} \\ & \vdots \\ & \max \left( {\min \mathop \sum \limits_{i = 1}^{m} Q_{{s_{i} }} \times \beta_{{s_{i} }} } \right) \le \gamma_{m + 2} \\ & {\text{s.t}}{. }m. \\ \end{aligned}$$

(18)

always be an integer and not a decimal number. Thus, ${M}_{\mathrm{w}}$ cannot be less than 1 as shown in (17).

The objective functions and multi-objective problem formulation that has been outlined in this section would be solved using the proposed advanced multi-objective particle swarm optimization approach, outlined in Sect. 4.

Methods

Particle swarm optimization (PSO) algorithm

In general, the particle swarm optimization algorithm is a widespread evolutionary algorithm that has been used a lot to solve single-optimization problems [42]. This algorithm is a random search method based on the behavioral pattern that simulates the way a swarm of birds forage and flock together. It has aspects that influence it based on the individual and social behavior of the birds (i.e., particles) in the swarm.

The PSO algorithm works in stages that include: initialization, searching, and updating best positions and values, converging with the best search results. All these processes are done over several iterations. The initialization phase of PSO is when a random set of particles or solutions to an optimization problem is generated. That is supposed to be representative of a swarm of birds. In the block selection problem, the initialization stage would give the random solutions for the number of blocks represented by $H_{{\text{f}}}$ that should be sent to the cloud. The selection is based on the constraint of the number of blocks N each peer can hold as shown in (19) and a given population side, Pop, which the user provides.

$$\begin{aligned} H_{{\text{f}}} & = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {M_{{s_{1} }}^{1} } & {M_{{s_{2} }}^{1} } \\ \end{array} } & \cdots & {M_{{s_{m} }}^{1} } \\ \vdots & \ddots & \vdots \\ {\begin{array}{*{20}c} {M_{{s_{1} }}^{z} } & {M_{{s_{2} }}^{z} } \\ \end{array} } & \cdots & {M_{{s_{m} }}^{z} } \\ \end{array} } \right). \\ & \left( {1 \le z \le Pop} \right) , \left( {1 \le M_{{s_{i} }}^{z} \le N} \right) , M_{{s_{i} }}^{z} \in {\mathbb{N}}. \\ \end{aligned}$$

(19)

The objective functions are also evaluated at this stage using the generated particles, and the results obtained from the objective functions are used to judge the fitness of the solutions. The next stage of searching and updating the solutions or particles' positions and values occurs by altering the search direction of the solutions to move them to the best solution in the search space. These alterations and adjustments are made based on the two extremums, the personal best solution ($P_{k}^{i} )$ of each particle $i$ and the global best solution of the whole swarm $(P_{k}^{g} )$. This is done in such a way that each particle in the swarm adjusts its position and direction to move toward the best result or solution that has been found and recorded by the whole swarm, which ensures that at the end of $K$ iterations, all solutions would be converging toward the best solution. The adjustments made to the velocity, $v_{k}^{i}$, and position, $x_{k}^{i}$ of each particle $i$ during every kth iteration are shown in (20) and (21).

$$v_{k + 1}^{i} = \omega \times v_{k}^{i} + c_{1} r_{1} \left( {P_{k}^{i} - x_{k}^{i} } \right) + c_{2} r_{2} \left( {P_{k}^{g} - x_{k}^{i} } \right).$$

(20)

$$\begin{aligned} & x_{{k + 1}}^{i} = x_{k}^{i} + v_{{k + 1}}^{i} \\ & 1 \le k \le K \\ & 1 \le i \le Pop. \\ \end{aligned}$$

(21)

From (20) and (21), $\omega$ represents the inertia weight which works with velocity to improve the calculation speed and the quality, i.e., makes it converge faster or slower. $r_{1}$ and $r_{2}$ represent random values that help incorporate and model the aspect of environmental interference that birds in a swarm may face $\left( {0 \le r_{1} ,r_{2} \le 1} \right)$. $c_{1}$ and $c_{2}$ are known as the acceleration coefficients or learning factors [43]. Each iteration produces a variation in $P_{k}^{i}$, which is the personal best solution of a particle until the maximum number of iterations is reached.

The significant advantage of the PSO algorithm is its fast convergence [42], but the major setback is that it is notoriously known to get trapped into the local optima, which sometimes ends up in excessive searching.

Time-variant inertia weight PSO with variable-period cosine function

Several methods have been proposed to improve the already impressive convergence of PSO and prevent excessive searching and trapping in the local optima. Some of these methods include the Random Inertia Weight (RIW) method [43], the linear time-variant inertia weight [44], and the nonlinear time-variant inertia weight combined with a quadratic function introduced by Chatterjee et al. [45].

Zhang et al. [46] proposed a time-variant inertia weight combined with a variable-period cosine function. Their proposal was a multistage inertia weight method that has three main stages. The initial stage where the inertia is kept large for the global search process prevents the PSO algorithm from getting trapped in the local optima. The intermediate stage where the inertia value drops, and there is a transition from the global search process to the local search process. A final stage where the inertia value is kept small till the maximum iterations are reached so that the PSO can converge to an accurate value. The mathematical formulation for the multistage inertia weight $\omega_{\cos } \left( t \right),$ is shown (22).

$$\begin{aligned} & \omega_{\cos } \left( k \right) = \frac{{\left( {\omega_{{{\text{ini}}}} + \omega_{{{\text{fin}}}} } \right)}}{2} + \frac{{\left( {\omega_{{{\text{ini}}}} - \omega_{{{\text{fin}}}} } \right)}}{2} \times \cos \left( {\frac{I\left( k \right)\pi }{K}} \right). \\ & I\left( {k + 1} \right) = I\left( k \right) + a, I\left( 1 \right) = 0. \\ & a = \left\{ {\begin{array}{*{20}l} {a_{1} , } \hfill & {\quad \frac{I\left( k \right) \le K}{6}} \hfill \\ {a_{2} , } \hfill & {\quad \frac{K}{6} \le I\left( k \right) \le \frac{5K}{6}} \hfill \\ {a_{3} , } \hfill & {\quad \frac{K}{6} < I\left( k \right) \le K} \hfill \\ \end{array} } \right.. \\ \end{aligned}$$

(22)

A term $I\left( k \right)$ is introduced into the cosine function to adjust the period, and it changes on every iteration. To keep track of the stage at which the PSO algorithm is in, another variable $a$ is introduced to help update $I\left( k \right)$. Based on experiments performed in [46], the values chosen for the $a_{i}$ values are as follows; $a_{1} = \left( \frac{4}{3} \right), a_{2} = \left( \frac{16}{3} \right)$ and $a_{3} = \left( \frac{2}{9} \right)$. A user can specify the starting initial inertia weight $\omega_{ini}$ and final inertia weight $\omega_{{{\text{fin}}}}$, but it is proposed to be set to $\omega_{{{\text{ini}}}} = 0.4$ and $\omega_{{{\text{fin}}}} = 0.9$.

Multi-objective particle swarm optimization (MOPSO)

MOPSO was first introduced by Coello and Lechuga [38] to deal with multi-objective optimization problems. Before its introduction, PSO could only handle single-objective optimization problems. Multi-objective optimization problems had to be condensed into single-objective problems using the weighted sum approach [47].

Two particles can determine which particle is the best for single-objective problems, but that is not the case when dealing with multi-objective problems. This is because there is more than one objective function and thus multiple fitness values to compare. Thus, the concept of the Pareto-optimality and dominance is introduced. This helps to tell whether a particle is better than another by ensuring each particle's targets are better than the current best, not one or two but all.

In MOPSO, apart from the updated population during every iteration, an external archive keeps track of non-dominated solutions (i.e., solutions with the number blocks to be sent to the cloud for each peer). These archive elements are referred to as the Pareto set, and the eventual goal is to have a Pareto optimal set. Elements are added to this archive until it is complete, and then the archive is sorted, and only the very best solutions are kept. This is where the update would be made to MOPSO for this paper.

When it comes to the global best search result, there would be more than one optimal solution because there are multiple objective functions described in Sect. 3. Thus, a global leader is chosen and used to adjust all other solutions. The flow chart for the MOPSO algorithm is shown in Fig. 4.

Fig. 4

Flow chart for the original MOPSO algorithm

Advanced time-variant multi-objective particle swarm optimization (AT-MOPSO) algorithm

Based on research on time-variant inertia weight and non-dominated Pareto sets, AT-MOPSO is proposed to improve the original MOPSO.

AT-MOPSO makes use of the time-variant inertia weight suggested in [46] to improve in the update process for the position $(x_{k + 1}^{i} )$ and velocity $(v_{k + 1}^{i} )$ values by the incorporating $\omega_{\cos } \left( k \right)$ as a replacement to the fixed $\omega$ in the original MOPSO equation.

The next update to the MOPSO is the incorporation of non-dominated sorting and mutation of the external archive $H_{{\text{f}}}^{\left( k \right)}$ adapted from the Non-Dominated Sorting Genetic Algorithm [48]. The mutation process randomly takes a subset of $H_{{\text{f}}}^{\left( k \right)}$, usually $Pop{/}2$, i.e., 50% of the total number of the external archive. For each solution, a set number of particles are picked at random. The position values for those particles are mutated using a mutation rate $\left( \mu \right)$ and mutation step size $\left( \sigma \right)$, as shown in Fig. 5.

Fig. 5

Mutation operation to create mutant particles

The updated positions are then based on the objective functions where the values are calculated and the number of blocks per fog node. The algorithm for the mutation is given in Algorithm 1.

After the mutant population (popm) is created, a joint set of the mutant population (popm) and the external archive $H_{{\text{f}}}^{\left( k \right)}$ is created, and this set is sorted, and the non-dominated solutions are found. The external archive $H_{{\text{f}}}^{\left( k \right)}$ is then updated with these non-dominated solutions. The entire algorithm for AT-MOPSO is given in the flowchart in Fig. 6. The major areas which have been improved and added to the original algorithm are indicated in orange.

Fig. 6

Flow chart for AT-MOPSO which is a proposed update to MOPSO

It must be noted that actual values will be put in the population $H^{\left( 0 \right)}$, the external archive $H_{{\text{f}}}^{\left( k \right)}$. The mutant population (popm) would all have to be integers since these solutions represent the number of blocks $M_{{s_{i} }}$ for each fog node that would be sent to the cloud. Thus, an extra step of ensuring that all solutions are converted to integers must be guaranteed across the whole algorithm for this use case.

Experiments and results

The AT-MOPSO algorithm is applied to the objective functions outlined in Sect. 3 of this paper, shown in (14)–(18). When the maximum number of iterations is reached, the external archive ${H}_{f}$ which contains the final Pareto set of non-dominated solutions, is filtered using the constraints set for each objective function ${\gamma }_{1}, {\gamma }_{2},\dots ., {\gamma }_{m+2}$. If any of the solutions has a corresponding objective function value less than ${\gamma }_{i}$, it is filtered out and removed from the external archive into a new set ${H}_{f}^{*}$. This would allow only for solutions that satisfy all constraints to be in ${H}_{f}$.

After the filtration step, we would still be left with some, Pareto optimal solutions, but we need the best solution out of the set ${H}_{f}^{*}$ to answer our research questions of how many blocks for each fog node must be sent to the cloud. This was done by iteratively going through each solution in ${H}_{f}^{*}$ and finding the minimum weighted sum of all objective functions using (23) where ${\delta }_{l} (1\le l \le m+2)$ represents the weights assigned to the individual objective function.

$${\text{WS}} = \mathop \sum \limits_{j = 1}^{m} \delta_{j} P_{{b_{j} }}^{\prime } + \delta_{m + 1} \cos t + \delta_{m + 2} Q .$$

(23)

To show our AT-MOPSO algorithm's potency, we ran it. We compared the results for the different objective functions against the original MOPSO, time-variant MOPSO (offered as I-MOPSO), and NSGA-III (shown as NSGA3). The experiments used for testing the algorithms were done on a computer with an Intel Xeon E5 processor with 2.9 GHz and 32 GB of RAM (the full specifications of the computer is shown in Table 1).

Table 1 Computer specifications that was used for the experiments

To simplify the experiment, we assumed a fixed query frequency ${F}_{0}$ of 0.95. The set value helps to depict a typical use case involving IoT fog nodes connected to a Blockchain with IoT devices being used in a traceability application such as [33] as described in Sect 3. Three fog node servers were selected; thus, the set $S=\left\{{s}_{1}, {s}_{2}, {s}_{3}\right\}$ and the number of blocks to be sent to the cloud for each fog node is ${M}_{{s}_{1}}, { M}_{{s}_{2}}$, and ${M}_{{s}_{3}}$ respectively, making $m=3$. For simplicity, the total number of blocks $N$ that can be stored for each fog node was taken to be 200 at a 1 MB size for each block. The local space occupancy weights for the individual fog nodes were set as ${\beta }_{{s}_{1}}, {\beta }_{{s}_{2}},$ and ${\beta }_{{s}_{3}}$. The constraints for the five objective functions (i.e., $m+2)$ were specified as ${\gamma }_{1}, {\gamma }_{2}, {\gamma }_{3}, {\gamma }_{4}$, and ${\gamma }_{5}$. Also, the weights ${\delta }_{1}, {\delta }_{2}, {\delta }_{3}, {\delta }_{4}$ and ${\delta }_{5}$ of each objective function for the weighted sum computation in (23) was also specified. A complete list of all parameters used for the experiment is specified in Table 2.

Table 2 List of parameters used for experiment for the different algorithms

For the implementations, the total number of iterations K was set to 200. For each iteration, averages of the solutions in the external archive were computed, and graphs plotted for F1, F2, F3, F4, and F5, representing each objective function as shown in Fig. 7. It must be noted that it takes some time for the algorithms to run for the given problem. This problem is not being run to the point of full convergence but rather to find the algorithm that can minimize the objective functions as much as possible in the run time.

Fig. 7

The graphs showing the performance of the objective functions for the different objective functions (i.e., F1, F2, F3, F4 and F5) when AT-MOPSO was used

The graph in Fig. 7 shows the results for the when the AT-MOPSO was compared to the original MOPSO algorithms as well as the NSGA-C (Non-Dominated Sorting Genetic Algorithm with Clustering). There is not research existing the direction of using optimization techniques to find solve this cloud storage block selection problem. The most recent scheme that has been used to solve this is the NSGA-C based on the NSGA-III algorithm proposed by Xu et al. [21]. It can be clearly shown from the results that our proposed scheme (AT-MOPSO) out-performed NSGA-C and the original MOPSO algorithm for the first four objective functions (i.e., F1–F4). It can also be observed that for the objective function F5, AT-MOPSO performs slightly worse than NSGA-C and the original MOPSO. However, the advantage AT-MOPSO and other PSO algorithms have over NSGA-III is they converge at a faster rate.

Thus, the results of the AT-MOPSO being slightly worse in F5 in comparison with NSGA-C, still gives it an edge over the NSGA-C due to the afore mentioned reasons. The benefits of the AT-MOPSO can be further elaborated by considering the energy efficiency or energy-saving analysis of the two algorithms.

We performed further investigations into how our proposed scheme compares to some of the common and popular Multi-Objective algorithms. In Fig. 8, we show our results when our developed scheme was compared to SPEA-II (Strength Pareto Evolutionary Algorithm) [49], PESA-II (Pareto Envelope-based Selection Algorithm with region-based selection) [50] and NSGA-III. Our scheme also out performs the SPEA-II and PESA-II algorithms with SPEA-II performing slightly better than PESA-II for the same block selection problem using the same parameters.

Fig. 8

Graphs showing how the AT-MOPSO algorithm performs in comparison to other well-known multi-objective optimization scheme

It can also be seen in Fig. 8, that our developed scheme (AT-MOPSO) is at par with NSGA-III in most of the objective functions (i.e., F1–F4) and even marginally out-performing NSGA-III in objective function F4. AT-MOPSO is also out-performed by NSGA-III in the results for objective function F5. For the same afore mentioned as NSGA-C (which is based on NSGA-III), AT-MOPSO should be selected due to its faster run time and convergence rate.

Discussion

We discuss the potency of our develop AT-MOPSO algorithm by taken a good look a critical energy efficiency comparison with other Multi-Objective Optimization algorithms. All the specifications of the computing resources used for this comparison is shown in Table 1. Shukla et al. [46] used the power consumption model for CMOS (Complementary Metal Oxide Semiconductor) logic circuits to analyze dynamic energy consumption on microprocessors. They considered that for microprocessors, the capacitive power or the dynamic energy consumption is the most significant factor, and thus they expressed it mathematically as shown in (24):

$$\begin{aligned} E_{{{\text{busy}}}} & = \mathop \sum \limits_{i = 1}^{n} B \times v_{i}^{2} \times f_{r} \times t_{i} \\ E_{{{\text{idle}}}} & = \mathop \sum \limits_{i = 1}^{n} B \times v_{{i_{{{\text{lowest}}}} }}^{2} \times f_{{r_{{{\text{lowest}}}} }} \times t_{{i_{{{\text{idle}}}} }} \\ E_{{{\text{total}}}} & = E_{{{\text{busy}}}} + E_{{{\text{idle}}}} \\ \end{aligned}$$

(24)

where $B$ is the constant parameter related to the dynamic power (based on DVFS—Dynamic Voltage and Frequency Scaling) for a given CPU, ${v}_{i}$ is the supply voltage at which the processor is regulated, ${f}_{r}$ is the clock frequency of the microprocessor, and ${t}_{i}$ is the time for which a microprocessor runs a task.

There were two considered cases where the processor is in an idle state ${E}_{\mathrm{idle}}$ and when the processor is running a task ${E}_{\mathrm{busy}}$. The times for which the various algorithms run the 200 iterations were recorded and are shown in Table 3. It can be seen from the results that the AT-MOPSO runs in also half the time it takes the NSGA-III algorithm to complete the 200 iterations with the given parameters. The time it takes to complete the same number of iterations using NSGA-C (the most recent scheme used to solve the block selection problem) is even more than that of NSGA-III. Xu et al. [21] considered their scheme to be a better approach due to the fact that it out-performed NSGA-III for the F5 objective function which represents that for local space occupancy (arguably the important objective).

Table 3 Results for the runtimes in seconds for different algorithms compared

We have succeeded in showing that our scheme out-performs NSGA-C in all other objective functions and further performs in an almost similar fashion as NSGA-C for objective function F5, yet running in less than half the time it takes to run NSGA-C. The recorded execution times were fed into (24) to calculate the energy consumed the runtime of each algorithm. The results for the energy consumed executing each of the algorithms are shown in the graph in Fig. 9. The algorithms' energy consumption is an essential factor to consider because this is a task the processor of the fog node would be running on a persistent basis, and having an optimization algorithm that can converge very fast and use less energy is an excellent feature to have.

Fig. 9

Results of energy consumption of the different optimization algorithms

Application of the at-MOPSO to a real-world industrial blockchain system for maintenance

To show the true potency of the developed algorithm and block selection approach, we incorporated it into a real-world industrial Blockchain maintenance system which was shown, proposed and tested in the BISS 4.0 platform [23]. We adapted the architecture and showed where the AT-MOPSO algorithm could prove useful and is shown in Fig. 10

Fig. 10

The improved BISS platform architecture with the AT-MOPSO incorporated and running on peer

In the original implementation of the BISS 4.0 platform, there is a combination of enterprise architectures, services and data to build a Blockchain system. The implemented Blockchain in the architecture is Hyperledger Fabric [51] which is a permissioned Blockchain, thus all the peers in the architecture can know each other without any form of trust since a permissioned Blockchains ensures the user groups that have access to the Blockchain is restricted.

The BISS platform has sensors and actuators being joined and connected to machines. These machines are in turn connected through an adapter (running a fabric client) to the main computing device that acts as a peer on the Blockchain. This is done so that all storage and computing tasks can be delegated to that peer. The downside of such an architecture is that the machine is not truly (but virtually) connected to the Blockchain. This approach of incorporating a Blockchain in an IoT enterprise system is one that is very common in industrial IoT systems. The said approach is very common due to the storage demands and processing power needed to run the machines that the sensors and actuators are connected to, due to the less potent nature of such machines. This is clearly shown in the BISS platform architecture.

By the use of the approach introduced in this paper, those machines can be brought closer to the Blockchain such that each machine can then act as a peer on the Blockchain. This means that machine with cheaper hardware and minimal storage space can be used as peers on the Blockchain. Our approach would enable this to happen because there would be a lower storage demand on the machine such that some of their blocks would be moved to the cloud for storage as shown in Fig. 10.

It must also be noted that in the incorporation of Blockchain into industrial systems and machines as shown in the BISS architecture, the machines are mainly going to be legacy and older systems so having such an algorithm to take some of the pressure of them would be greatly appreciated by operators of such systems and provide a true connection between the machines and the Blockchain.

In the version of BISS which incorporates our approach, machines which house the sensors and actuators are now peers on the Blockchain and they would in turn be running the AT-MOPSO algorithms. From our pilot testing of the algorithm, it was observed that as the machines run the given algorithm, they are able to offload some of the blocks that are produced from transactions in their ledger to the cloud and this reduced the transaction time by 52%. The is because, the AT-MOPSO takes into consideration (as a parameter), the amount of storage space that the peer on the Blockchain has available, thus the optimization is done based on the provided value. The three main objective functions that the block selection is based on takes into account the cost of storage of the blocks in the cloud as well as local storage occupancy. All these afore-mentioned factors, make the developed and proposed algorithm one that can be put to great and diverse use as shown with this industrial application example.

Conclusion

In this paper, we looked at the integration of Blockchain with IoT applications. We proposed a hybrid Blockchain-IoT integration scheme that used fog computing and cloud storage to help improve the throughput of such applications. The scheme scheduled a side-chain run on a fog node and only sent completed transactions in the side-chain to the main Blockchain. The proposed scheme alleviates the storage pressure on fog nodes by ensuring that some of the blocks produced by the transactions are stored in the cloud for each connected fog node.

To select the number of blocks that should be sent to the cloud, we further proposed an Advanced Time-Variant Multi-Objective Particle Swarm Optimization (AT-MOPSO) algorithm to help solve the block selection problem. The algorithm was applied to objective functions formulated to model the aspects of the query probability of the blocks on each fog node, the cloud storage cost to be incurred by a user, and the local space occupancy/storage availability needed to be saved for each fog node. We compared our proposed algorithm to the original MOPSO algorithm and the Time-Variant MOPSO and NSGA-III. We observed that our scheme performed better in all objective functions than all other MOPSO algorithms except for the local space occupancy. Our AT-MOPSO algorithm also performed as well as the NSGA-III algorithm for the query probability objective function for the first and third fog nodes, and also for the cloud storage cost objective function. We also assessed our proposed AT-MOPSO algorithm to determine its energy-saving efficiency compared to the NSGA-III algorithm (which is the current standard or algorithm which has been used to solve this problem). Our algorithm runs in about half the time of the NSGA-III and achieved about 52% energy efficiency compared to the NSGA-III.

We further showed how our proposed algorithm can be incorporated into industrial systems which are running legacy machinery. This was shown but adapting the BISS platform architecture and showing where our AT-MOPSO would fit in it.

In our future work, we plan to explore the possibilities of reducing the algorithm's runtime time even further, thus allowing us to deal with fog nodes with larger storage sizes of about 1TB or more. It will also be worth looking at the effects of our algorithm on aspects of the IoT devices such as Quality of Service (QoS) and transmit power limitations.