Collaborative neighbor discovery in directional wireless sensor networks: algorithm and analysis

Abstract

In directional wireless sensor networks (DSNs), sensor nodes with directional antennas provide extended network lifetime and better coverage performance. However, one of the key challenges of directional nodes is to discover their neighbors due to difficulty in achieving synchronization among their directed transmissions and receptions. Existing solutions suffer from high discovery latency and poor percentage of neighbor discovery either due to lack of proper coordination or centralized management of the discovery operation. In this work, we develop a collaborative neighbor discovery (COND) mechanism for DSNs. Each COND node polls to directly discover its neighbors in a distributed way and collaborates with the already discovered nodes so as to allow indirect discovery. It helps to increase the neighbor discovery performance significantly. A Markov chain-based analytical model is developed to quantify theoretical performances of the proposed COND system. The performance of the COND system is evaluated in Network Simulator Version 3, and simulation results reveal that it greatly reduces the discovery latency and increases neighbor discovery ratio compared to state-of-the-art approaches.

Introduction

In directional wireless sensor networks (DSNs), sensor devices with directional antennas sense data and deliver them in a multihop fashion toward the sink node. Nowadays, DSNs are being used for the implementation of many real-time applications including infrastructure monitoring, health-care monitoring, robotic exploration, battlefield surveillance, target tracking, and disaster response [1, 2]. The directional sensors have been proved to provide better energy efficiency, sensing quality, bandwidth utilization, etc. [3, 4]. However, the directional transmissions and receptions of the sensor nodes have made the development of data communication and networking protocols for DSNs more challenging.

Neighbor discovery is defined as the problem of identifying all nodes within the communication range of a sensor device. The problem of neighbor discovery in directional sensor network not only is more challenging than that in its omnidirectional counterpart but also requires complete redesign and implementation. The key fact behind this requirement is that the directional nodes have limited width of communication sectors, and thus, two nearby nodes must steer their communication sectors to each other for a successful communication [5–7]. Efficient strategies need to be employed so that a pair of neighbor nodes eventually beamform their antennas to each other at a certain time instance and can discover themselves. The primary challenge lies in increasing the number of nodes discovered in bounded delay through better coordination in a distributed way, when the nodes are not clock-synchronized.

In the literature, the problem of neighbor discovery with omnidirectional antenna has well been explored [1, 8]. Nevertheless, recently, a few neighbor discovery mechanisms are developed that are based on directional communications. A neighbor discovery algorithm based on contention-based and contention-free approaches have been developed in [8], where only the sink node uses directional antenna, whereas the other nodes use omnidirectional one, resulting in asymmetry-in-gain problem [9, 10]. A scan-based asynchronous neighbor discovery algorithm (SBAN) is proposed in [11], where the neighbor discovery is based on fully directional transmissions and receptions. The probabilistic HELLO message broadcasting with fast reply mechanism reduces collisions among the sensors. A randomized two-way neighbor discovery algorithm has been developed in [12]. The authors have presented an asymptotic analysis of one-way and two-way directional neighbor discovery algorithms and have designed a two-way neighbor discovery mechanism with selective feedback that reduces the neighbor discovery time. However, both the works [11, 12] lack in guaranteeing responder the reception of reply packets which increases the discovery latency for a dense network. A fully directional and centralized sectored antenna neighbor discovery (SAND) algorithm is developed in [13], where a token is passed among the nearby nodes to successfully learn each other. However, for token management, a central node is required that is not feasible for many applications of DSNs, especially in achieving scalability. Moreover, the rotational latency of a token affects the neighbor discovery accuracy and it increases the overall neighbor discovery latency. None of these works have well-thought-out the directional coordination between two nodes.

In this paper, a collaborative neighbor discovery (COND) algorithm is proposed, where the directional sensors discover their neighboring nodes collaboratively by sharing the discovered neighborhood information with the surrounding nodes. The key idea behind the COND mechanism is that each directional node performs neighbor discovery in each sector using a contention-based polling mechanism. The goal of neighbor discovery mechanism is to increase the number of discovered nodes with minimum delay using a two-way collaborative polling mechanism. The preliminary concept of this work has been published in [14]. In this paper, we augment the detail operation method of indirect neighbor discovery through collaboration. We carry out theoretical analysis using Markov chain model that quantifies expected number of discovered neighbors and the corresponding delay incurred. We also present performance analysis and results for average discovery latency per node, sensing wastage, and energy cost per neighbor discovery. The results show that the proposed COND mechanism greatly outperforms the state-of-the-art systems—randomized two-way [12] and SAND [13].

The main contributions of this work are summarized as follows:

• A fully distributed novel neighbor discovery mechanism, collaborative neighbor discovery (COND) algorithm is developed for sensor nodes in DSNs.

• A two-way polling-based collaborative mechanism is designed to decrease the possibility of conflict and to speed up the handshaking process. In this mechanism, each node learns about its neighbors collaboratively by direct and indirect neighbor discovery through sharing information of already discovered nodes to and from its neighbors.

• We develop a Markov chain model to analyze theoretically the expected number of neighbors discovered and the number of iterations required for discovery.

• Finally, the results of performance evaluations, carried out in Network Simulator Version 3 (NS-3) [15], show that our proposed COND mechanism outperforms SAND and randomized two-way mechanisms in terms of neighbor discovery latency and ratio, energy consumption, etc.

The rest of the paper is organized as follows. We give a detailed description of related state-of-the-art works in Section 2. In Section 3, we describe the network model and assumptions. The proposed algorithm for the neighbor discovery using directional antenna is discussed in detail in Section 4, and the theoretical analysis and performance studies for the given algorithm are discussed in Sections 5 and 6, respectively. Finally, we conclude the paper in Section 7.

Related work

Directional sensor networks (DSNs) are gaining much popularity in the recent years, due to their improved performance gains through directional antennas [7, 16–21]. Even though the problem of neighbor discovery was well investigated in the literature for omnidirectional and wireless ad hoc networks, that for directional sensor networks kept less focused. However, in recent years, we find a few of neighbor discovery algorithms that are based on directional antennas. The existing works can broadly be categorized in two types: one-way broadcasting mechanisms [22–27] and two- or three-way handshaking mechanisms [11, 13, 14, 28–30].

In one-way broadcast-based neighbor discovery mechanisms, nodes periodically broadcast their presence. On reception of at least one message successfully, a nearby node discovers the sender node. A probability-based neighbor discovery algorithm, namely I-SBA is proposed in [27], where nodes transmit, receive, and remain idle with certain probabilities. The mechanism decreases number of collisions among the neighboring nodes when the probabilities are selected properly. Nevertheless, with the growing number of nodes in the network, the possibility of directional synchronizations among the nodes is gradually decreased. In [23], authors develop a directional neighbor discovery mechanism where the number of slots for neighbor discovery is dependent on the order of the average number of nodes in the network. The base station sends a beacon signal toward all the nodes in the network to start the discovery process, and all the nodes are time-synchronized with each other. Their neighbor discovery mechanisms exploit hybrid usage of omnidirectional and directional antennas; hence, with the increasing number of nodes in the network, the mechanism initiates extra overhead for the node synchronization. A directional neighbor discovery protocol was developed in [25], which is based on one-way broadcast mechanism. A HELLO message is broadcasted by each node, and after hearing the message, the neighboring nodes learn about information of that node.

In none of the above one-way broadcast-based neighbor discovery mechanisms, the sender nodes know whether the neighboring nodes receive their message successfully or not. Thus, the one-way neighbor discovery algorithms might be suitable for omnidirectional networks but not for directional sensor networks, because the later requires synchronization between the transmitting and receiving nodes to make the communication a successful one. Therefore, two- or three-way handshaking protocols are more desirable for DSNs.

In two-way handshaking-based neighbor discovery mechanisms, a receiver node, after reception of a message, sends back a REPLY message toward the sender node, facilitating both nodes to discover each other in one event of communications. In directional transmission, a receiver node can only hear the message if it faces its antenna toward the sender and thus a feedback message is very important for neighbor discovery among the nodes. Hence, at least two-way handshaking is required for effective directional neighbor discovery as the nodes can agree on a future period for communication after the discovery. A fully directional scan-based asynchronous neighbor discovery algorithm is proposed in [11], where each node senses the medium and transmits HELLO message in a random direction and gathers location of the neighbor nodes, reducing the number of collisions among reply packets.

The urgent requirement of synchronization in between a transmitter and a receiver is kept unexplored in the above works. Moreover, nodes wait at each sector for a fixed period of time for neighbor discovery, which is highly inefficient. In [29], a directional neighbor discovery mechanism has been developed, where only the sink node of the network uses directional antenna, whereas the other sensors use omnidirectional antennas. The sink node applies contention-based and cotention-free methods to medium access and sequentially scans all its sectors to discover its neighbors. To minimize the medium access delay, the authors presented an optimization method for selecting the beam width and the persistence probability of neighbor discovery. This mechanism results asymmetry-in-gain problem [9] due to the difference between the antenna gain patterns of the sink node and other sensors. A randomized two-way neighbor discovery mechanism is proposed in [12], where the authors have presented an asymptotic analysis of one-way and two-way directional neighbor discovery algorithms. Their two-way neighbor discovery mechanism exploits selective feedback policy so as to reduce collisions among the reply packets and thus to decrease neighbor discovery time. However, the reception of a reply packet is not certain in the above works due to lack of synchronization between the sender and receiver nodes.

A fully directional and centralized three-way sectored antenna neighbor discovery (SAND) algorithm is proposed in [13], where a token is passed among network nodes sequentially to discover their surrounding neighbors. However, for token management, it requires a central node, which is not only often infeasible for many DSN applications but also limited by scalability. Furthermore, the rotational latency of a token affects the neighbor discovery accuracy and increases the overall neighbor discovery latency. The SAND mechanism also has not considered the directional synchronization issue among the nodes, causing deafness problem, and as a central controller controls the whole mechanism, the discovery latency sharply increases.

Our work is different from the above studies in that we develop a fully distributed neighbor discovery mechanism, where both the transmissions and receptions are directional and nodes collaborate with their (already discovered) neighbors to find other neighbors, reducing neighbor discovery latency significantly. This indirect neighbor discovery and selective feedback policies jointly help our algorithm to decrease the collisions in the network. In addition to that, a COND node employs dynamic waiting time at different directions while discovering nodes in the neighbor that greatly helps to mitigate the deafness problem.

Network model and assumption

We assume a directional sensor network of an area A where a set $\mathcal {S}$ of directional sensor nodes are deployed with uniform random distribution, resulting in deployment density,

$$ \rho = \frac{|\mathcal{S}|}{A}. $$

(1)

Each node is designed with $\mathcal {M}$ sectored switched-beam directional antennas, as shown in Fig. 1. To cover the whole azimuth, fixed number of fixed beam width antenna elements is attached in each antenna of a sensor. Each node can activate one sector at a particular time. Nodes can switch from one sector to another by activating different antenna elements, and each element has high antenna gain to a particular sector. Basically, they direct a major or almost their entire signal in just one direction instead of dispersing all around a 360° circle. Typically, the switching delay from one sector to another is 5×10⁻⁶ μs for a traditional switched beam directional antenna [13, 31].

Fig. 1

Antenna model for each node

Each node has one transceiver and can form one directional beam in a sector at a given time. For the network nodes, all transmissions and receptions are directional and they do not require any additional omnidirectional antenna. Note that the usage of both directional and omnidirectional antennas causes additional hardware cost, complexity, and two other major problems. First, the transmission ranges of the omnidirectional antenna and directional antenna are different, which introduces asymmetry gain problem in communication links. Again, the spatial reuse benefits are greatly reduced since omnidirectional communication inhibits more simultaneous transmissions.

The communication radius (r) of all nodes in the network is homogeneous. Nodes in the network are not clock-synchronized with each other. Each node independently discovers its neighbors. The success event of a transmission is probabilistic; however, our dynamic polling period and selected response REPLY to HELLO messages decrease the probability of collision and increase the number of successful transmission events. If the discovery message is exchanged between two nodes for at least half of a slot, two nodes can discover at the same time slot [7]. Subsequently, in a distributed system, without any clock synchronization, two sensor nodes can discover each other within a bounded delay.

Initially, a node learns its position using a localization method [32]. We assume that the time is divided into contiguous slots and all nodes independently discover their neighbors within a bounded time. The total time frame is logically separated into transmit and receive time slots. Each slot is further divided into multiple mini-slots. A node either transmits HELLO message or listen to the medium for any message from its neighbor(s) in an individual slot. While communicating with each other, a node can identify the angular position of its neighbor by capturing its spatial signature vector [29]. After the deployment of the sensor nodes in the network, nodes discover their neighbors using COND mechanism, and during the neighbor discovery period, all the nodes will be active to discover most of the neighbors within short period of time. Later, the sensors collect sense data and start data transmission toward the sink node. An underlying medium access control protocol (e.g., S-MAC [33], T-MAC [34], B-MAC [35], DMAC [36], SAMAC [18]) can determine and control the energy-saving states of a sensor node, which is beyond the scope of this work. The notations used in this paper are summarized in Table 1.

Table 1 List of notations

Collaborative neighbor discovery mechanism

In this section, we present detail operation method of the proposed two-way collaborative neighbor discovery algorithm, COND, for DSNs. Each COND node tries to explore maximum number of neighboring nodes in different sectors. A COND node stays in each of its sectors for a particular time duration and performs direct and indirect neighbor discovery processes using polling mechanism. Unlike [11, 13, 30], we allow COND nodes to dynamically vary the time duration operating in a sector based on percentage of its neighbors already discovered. Furthermore, unlike in our previous work [14], we allow COND nodes to explicitly track the neighbors discovered indirectly and take actions differently, facilitating to increase the neighbor discovery performance. In summary, the COND mechanism is condensed into the following three steps:

• Initialization of neighbor discovery with appropriate value of a delay tuning parameter ($\mathcal {K}$)

• Discovery of neighbor nodes in different sectors using contention-based polling mechanism

• Maintaining and updating the neighbor tables of COND nodes in collaborative fashion

What follows next, we present the detail operations of the COND steps.

Initialization

Each node in the network first calculates the approximate number of neighbors around them after the deployment of the nodes in the network. The expected number of neighbors of each node can be calculated as

$$ E_{n} = \rho \times \pi \times r^{2}, $$

(2)

where r is the communication radius of a sensor node and ρ is the node deployment density. Then, the expected number of neighbors in a particular sector $m \in \mathcal {M}$ of a node is given by

$$ \mathcal{N}_{e}^{m} = \frac{E_{n}}{|\mathcal{M}|}. $$

(3)

Initially, each sensor node $s \in \mathcal {S}$ starts to explore neighbors in all of its sectors $m \in \mathcal {M}$ by switching its direction clockwise after a certain interval of T seconds. T is the time interval for staying in a particular sector of each node. As we are assuming that each node switches its sector one by one for neighbor discovery, it is necessary to stay in a particular sector for a certain period so that two nodes can steer their antennas to each other in that period. Hence, T depends on the number of sectors of a node and the delay incurred for switching a direction, and it is determined as follows:

$$ T = T_{\text{switch}} \times (|\mathcal{M}|-1) \times \mathcal{K}, $$

(4)

where T _switch is the switching delay and $\mathcal {M}$ is the set of sectors. Furthermore, when a good number of nodes are discovered in a particular sector of a node, it must stay less period of time over there so as to reduce the discovery overhead. On the other hand, when a node has discovered very less number of neighbors in a sector, it must stay longer period in that particular sector in order to reduce the discovery latency. Thus, for determining the value of time period T, we introduce a delay tuning parameter $\mathcal {K}$ that is updated after each iteration depending on the number of discovered neighbor nodes in a particular sector as follows:

$$ \mathcal{K} = \delta_{m} \times \mathcal{K}, $$

(5)

where the value of δ _m is chosen in such a way that the discovery latency in each sector $m \in \mathcal {M}$ is minimized. If a node discovers most of its neighbors in a given sector $m \in \mathcal {M}$, then it is wise for the node to stay for less period of time there and vice-versa; otherwise, discovery overhead will unnecessarily be increased. Thus, the value of δ _m helps us to dynamically control the staying period of a sensor node in a certain sector $m \in \mathcal {M}$ for neighbor discovery. Let $N^{m}_{d}$ represents the percentage of nodes that are already discovered in sector $m \in \mathcal {M}$, then the value of δ _m is determined as follows:

$$ \delta_{m} = \left\{ \begin{array}{ll} 2.0, & N_{d}^{m} \le 30\%, \\ 1.5, & N_{d}^{m} \le 50\%, \\ 1.0, & N_{d}^{m} \le 80\%, \\ 0.5, & N_{d}^{m} > 80\%. \end{array} \right. $$

(6)

Note that the numerical values in Eq. (6) are not strict choices; rather, the values are depicted through numerous simulation experiments for a given network environment (stated in Section 6), and they are tunable by the network administrator. In the case the number of already discovered nodes in a certain sector crosses the expected number of neighbors, the node may stop staying in that sector. Hence, it may happen that a node misses a good number of neighbors to discover if the calculation of expected number of neighbors is incorrect (due to distortions in deployment). Therefore, we allow a COND node to continue the discovery process until it fails repeatedly (say, up to two iterations) to find a new neighbor in a particular sector.

Contention-based polling mechanism

The COND nodes contend among them to poll their neighbors in different sectors so as to discover those. The frame structure followed by the polling mechanism contains ‘H’ (Hello) and ‘L’ (Listen) slots, as shown in Fig. 2 a. In H slots, a node broadcasts HELLO messages in random time slots with persistent probability P _t . In the remaining slots, the node listens to the medium for any HELLO message from the neighboring nodes.

Fig. 2

Frame structure and neighbor discovery in COND system. a Frame structure. b Neighbor discovery

Each slot is further divided into several mini sub-slots, as shown in Fig. 2 a. If a node decides to transmit a HELLO message in a slot, it does so in the first mini-slot and listens to the channel for any REPLY message(s) from its neighboring node(s). The HELLO message contains the node’s ID, (x,y) coordinate, sector number, and neighbor table, i.e., $\Gamma _{H} = \{ID,\ \text {coord}(x,y),\ m,\ \mathcal {T}\}$. On reception of HELLO message, the surrounding nodes update their neighbor tables and relay back their information in a randomly chosen mini-slot. Thus, the nodes develop their neighbor tables for each sector with so far discovered nodes. The structure of the neighbor table is represented by the tuple, $<ID, \text {coord}(x,y), m, \mathcal {F}>$, where the fourth field is a flag that contains 1 if the designated neighbor is discovered through direct exchange of messages and 0 if it is discovered indirectly. The details of direct and indirect discovery processes are discussed in the following section.

Collaborative discovery of neighbor nodes

The key challenge in reducing neighbor discovery latency in DSNs is the synchronization of HELLO-REPLY transmissions among the nodes in a neighborhood. Therefore, in addition to discover neighbors through direct exchange of messages, we allow COND nodes to share their neighbor tables with each other and to update their tables collaboratively so as to further decrease the discovery latency. Thus, some neighbor nodes are discovered indirectly (via other nodes).

Direct discovery

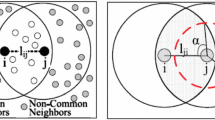
When two nodes are beamformed to each other and successfully exchange HELLO and REPLY messages, they can directly discover each other. After the HELLO-REPLY handshaking, two nodes update their neighbor tables accordingly. Thus, it is highly dependent on the synchronization of corresponding sectors of two neighbors. In Fig. 2 b, when the node a discovers a neighbor node b through direct handshaking, the flag entry for b in a’s neighbor table is set to 1. Unlike existing works in the literature that depend only on direct discovery, we allow indirect discovery of neighbor nodes through collaboration among them.

Indirect discovery

In omnidirectional communication, only direct discovery is sufficient for neighbor discovery. For directional nodes, it is the most important that two nodes are beamforming their antennas to each other; otherwise, the handshaking between the nodes would never occur. So, it may happen that when a node is broadcasting HELLO message in a particular sector, some of the neighbor nodes cannot receive the message because of the deafness problem [9]. Hence, the strict requirement of directional synchronization among nodes upsurges the discovery latency among the sensor nodes.

Consider a scenario in Fig. 2 b, where pairs a and b and a and c have already discovered themselves in the present or previous time frame, but node b has not yet been discovered by c or vice-versa, as their antenna directions did not match during the direct neighbor discovery process. In order to ease the problem and to accelerate the discovery process, we allow COND nodes to share their neighbor tables with already discovered nodes. That is, node a shares its table with b and c so that they can discover each other as a neighbor of the respective sectors by checking their coordinates. We term this update of neighbor table as indirect discovery, and the flag entry for such discovered node is set to 0.

The proposed collaborative neighbor discovery (COND) mechanism has been summarized in Algorithm 1. Initially, the neighbor table of each node remains empty. After getting a HELLO/REPLY message from any neighbor, a node updates its own table (lines 6–23). The node that receives a HELLO message checks its neighbor table to find whether the node is discovered earlier or not. If there exists a record, the node checks the flag value and if the value is 1, it does not give any REPLY message to that node assuming that it has exchanged messages in the earlier slots with that node; otherwise, it updates the information in the neighbor table and sends a REPLY message in a random sub-slot to the direction of the sender node (lines 15–22). If the sender node receives a REPLY message (without any collision) from any neighbor, it adds the node in the neighbor table (lines 8–12). In this way, two nodes discover each other using two-way handshaking. In the case, a node cannot discover any new node in a certain sector in consecutive two iterations, we stop COND process in that sector (lines 25–27).

The time complexity of Algorithm 1 for one iteration is quite straightforward to follow. The lines 1–31, enclosed in a loop, iterate $|\mathcal {M}|$ times having a complexity of $\mathcal {O}(|\mathcal {M}|)$ in the worst case. Again, the statements 4–23 iterate |T| times in a nested loop. The rest of the statements have constant unit time complexities. Therefore, the overall time complexity of the proposed COND algorithm is $\mathcal {O}(|\mathcal {M}| \times |T|)$.

Theoretical analysis of COND

At each iteration, a COND node performs neighbor discovery around its all sectors, and on completion of one iteration, the node gets an updated neighbor table with the newly discovered neighbors. In this section, we formulate a theoretical model for analyzing the neighbor discovery delay, average number of discovered nodes per iteration, and corresponding energy consumption of the COND system.

Discrete time Markov chain model

We have developed a discrete time Markov chain model for analyzing the performance of the proposed algorithm. In this model, a node can stay in one of the following six states: idle (I), Transmitting HELLO message (T), Listening REPLY message (L), Receiving HELLO message (R), Transmitting REPLY message (A), or Collided (C).

Here, L is the set of REPLY message listening states, i.e., $L = \left \{ L_{0}^{2},\ L_{1}^{2}, \dots,\ L_{v}^{2} \dots L_{0}^{u},\ L_{1}^{u}, \dots, L_{v}^{u} \right \}$ and each $L_{v}^{u} \in L$ denotes that the v number of neighbor nodes is discovered in reply mini-slot u. Similarly, R is the set of states after receiving a HELLO message, i.e., $R = \left \{ R_{0}^{1},\ R_{1}^{1}, \dots,\ R_{v}^{1} \right \}$, where each state $R_{v}^{1}$ represents that the v number of neighbors is discovered during the first mini-slot. The value of u is from 2 to the number of mini-slots (x ^′) available in a slot and the maximum value of v can be $\mathcal {N}_{e}^{m}$, the expected number of neighbors in a certain sector m.

Figure 3 shows the state transition diagram of the COND mechanism. Given that a node transmits HELLO message with probability P _t , we can calculate the idle state (i.e., listening for any HELLO message) probability for a node as follows:

$$ P_{I} = 1 - P_{t}, $$

(7)

Fig. 3

State transition diagram for the COND mechanism

where P _t is the probability that a node transmits HELLO message in a given slot. Suppose, a COND node a has sent a HELLO message in sector m. Another node b can only receive this HELLO message if it beamforms the antenna toward a in sector m ^′, where m≠m ^′ and |m−m ^′|=1 for three sector nodes, |m−m ^′|=2 for four sector nodes, etc. The joint probability that the two nodes a and b will beamform to each other is thus calculated as follows:

$$ {}P((b,m^{\prime}),(a,\!m)) = P((a,m) \times P((b,m^{\prime})|(a,m)) = \frac{1}{m^{2}}, $$

(8)

where the event (a,m) represents that the node a beam forms its antenna in sector m. Hence, in a given slot, a node a changes its state from I to T with probability,

$$ {}P_{T} = P((b,m^{\prime}),\ (a,m)) \times P_{t}^{a} \times (1 - P_{t}^{b}) \times (1-P_{t})^{\mathcal{N}_{e}^{b,m^{\prime}}-1}, $$

(9)

where the last part $(1-P_{t})^{\mathcal {N}_{e}^{b,m^{\prime }}-1}$ denotes the probability that no other nodes except a in the sector area of node b is transmitting any HELLO message at that time slot. Similarly, the receiving node b changes its state from I to R with probability,

$$ {}P_{R} \,=\, P((a,m^{\prime}),\ (b,m)) \times P_{t}^{a} \times (1 - P_{t}^{b}) \times (1-P_{t})^{\mathcal{N}_{e}^{b,m}-1}. $$

(10)

Therefore, the probability of occurring a collision event is given by

$$ P_{C} = 1 - (P_{I}+P_{T}+P_{R}). $$

(11)

Note that, on successful reception of HELLO or REPLY messages, a node discovers neighbor(s) directly or indirectly in one of the L or R states. The probability of discovering v number of nodes in a mini-slot is

$$ \sigma_{v} = \sigma^{d} \times \sigma^{i}_{v-1}+ \sigma_{v}^{i}, $$

(12)

where σ ^d=μ×P _R is the probability that the sender node is directly discovered; μ is a binary variable representing whether the sender node is already discovered (μ=0) or not (μ=1). The receiver node indirectly discovers a neighbor with probability, σ ⁱ=η×P _R , where binary variable η=1 if there remains a node in the sender’s table that is not yet discovered and is located in the sector area of the receiver node. Thus, the probability that the k number of neighbors are indirectly discovered in a mini-slot is given by

$$ \sigma_{v}^{i} = \binom{\mathcal{N}_{e}^{m}}{v} \times \left(\sigma^{i}\right)^{v} \times \left(1-\sigma^{i}\right)^{\mathcal{N}_{e}^{m} - v}. $$

(13)

Now, the probability that no neighbor is discovered in a mini-slot is given by

$$ \sigma_{0} = 1 - \left(\sigma^{d} + \sigma^{i}\right). $$

(14)

Note that, after receiving a HELLO message successfully from a sender node a, the receiver node b sends back a REPLY message to the sender a if any of the following three conditions is met: (i) the information of a is not present in b’s neighbor table, (ii) the node a is discovered indirectly, and (iii) the node b finds that $\mathcal {T}_{b} \backslash \ \mathcal {T}_{a} \ne \phi$. Let P _A denotes the probability of occurring any of the above events. Thus, the receiver node b transmits a REPLY message with probability P _A ; otherwise, it returns to idle state. The probability distribution vector, S, at a given time slot x at equilibrium is expressed as

$$ \mathbf{S} = \left[ S_{I} \quad S_{T} \quad S_{v}^{u} \quad S_{v}^{1} \quad S_{A}\quad S_{C}\right]^{^{x}}. $$

(15)

We can find the distribution vector at equilibrium by solving the equations P S=S and $\sum \mathbf {S} = 1$.

The solution of the above two equations is given below,

$$ s = \frac{1}{\xi} \times\left[ \begin{array}{c} 1 \\ P_{T} \\ \sigma_{0} \times P_{T} \\ \vdots \\ \sigma_{v} \times P_{T} \\ (\sigma_{0})^{2} \times P_{T} \\ 2 \times \sigma_{0} \times \sigma_{1} \times P_{T} \\ \vdots \\ P_{T} (2 \times \sigma_{v} \times \sigma_{1} + (\sigma_{2})^{2} + \sigma_{0} \times \sigma{4} + \sigma{4}) \\ \sigma_{0} \times P_{R} \\ \vdots \\ \sigma_{v} \times P_{R} \\ P_{A} \times P_{R} (\sigma_{0} + \sigma_{1} + \sigma_{2} + \sigma_{3} + \sigma_{4} + \dots \sigma_{v}) \\ P_{C} \\ \end{array} \right], $$

(16)

where ξ=1+P _T +(σ ₀+σ ₁+σ ₂+σ ₃+⋯+σ _v )(P _T +P _R +P _A P _R )+P _T [(σ ₀)²+2σ ₀ σ ₁+2σ ₀(σ ₁)²+2σ ₀ σ ₁ σ ₂ σ ₃+2σ ₀ σ ₁(σ ₂)² σ ₃(σ ₄)²+⋯+(P _T )²]+P _C .

The performance of the proposed COND mechanism greatly depends on the number of discovered neighbors in a time frame. From the Markov chain analysis we find the total number of neighbors discovered per slot. Thus, the expected number of discovered neighbors by a particular node is

$$ E_{v} = \sum\limits_{x=1}^{T} \left[ v \times \sigma_{u}^{v}(x) + v \times \sigma_{1}^{v}(x)\right]. $$

(17)

Now, the neighbor discovery rate ζ of a particular node is

$$ \zeta = \frac{E_{v}}{T}. $$

(18)

Figure 4 a, b shows the number discovered nodes and required number of iterations for the varying number of nodes in the network when there are 15 slots in a time frame and each slot has three mini-slots.

Fig. 4

Theoretical analysis for varying number of sensor nodes. a Neighbor discovery. b Required iterations

Comparison of analytical and simulation results

In this section, we compare the simulation experiment results with those of theoretical analysis. We perform our simulation experiments in NS-3 for varying number of sensors, ranging from 5 to 50. We have fixed the transmission range of each node at 100 m and the number of sectors at 4. With the growing number of sensors in the network, the number of discovered nodes increases linearly in both theoretical and simulation results, as shown in Fig. 5 a. Unsurprisingly, as depicted in graphs of Fig. 5 b, the number of iterations also increases with growing number of nodes both in theoretical and simulation results. However, the rate of increase is not that much higher because of the incorporation of indirect discovery in COND. Finally, the graphs of Fig. 5 a, b show that the analytical results are quite closer to simulation outcomes in estimating the number of discovered neighbors and the required number of iterations for neighbor discovery.

Fig. 5

Comparison of results from theoretical analysis and simulation experiments. a Neighbor discovery. b Required iterations

Performance evaluation

We have implemented our proposed COND system in NS-3 [15], a discrete-event network simulator to verify the effectiveness of proposed algorithm. We have done a comparative study of COND performances with those of two state-of-the-art algorithms—randomized two-way neighbor discovery mechanism [12] and SAND [13].

Simulation environment

We use wifiSimpleAdhocGrid model for sensor nodes and YansWifiPhy model to define the channel properties such as propagation and loss characteristics. Each node has the information about network density, and it calculates the expected number of neighbor nodes in each sector based on that information. The COND mechanism stops when no neighbor is discovered in two subsequent rounds. The simulation configuration parameters are shown in Table 2. We run the simulation experiments 30 times with different random seed values and take the average of the results for each graph data points.

Table 2 Simulation parameters

Performance metrics

• Average discovery latency per node: A round of node discovery is completed when a node finishes the operation in all sectors (either clockwise or anti-clockwise). Average discovery latency per node is the ratio of total discovery time to the number of discovered nodes.

• Sensing wastage is the count of wastage of time slots for neighbor discovery. A sensing time slot is regarded as wastage if no neighbor is discovered in it.

• Average discovery ratio is the ratio of the number of neighbor nodes successfully discovered to the total number of nodes in the network.

• Control byte overhead is the ratio of total number of control bytes (HELLO and REPLY messages) exchanged during the simulation period to the total number of neighbors discovered.

• Average energy cost per node discovery is the measure of average amount of energy consumed during the simulation period for discovering a single node in the network.

Simulation results

The comparative performance results are plotted for varying number of sensors deployed in the network, number of sectors a node has, and the size of the sensing time frame.

Impacts of varying number of nodes

We have varied the number of nodes from 100 to 1000 and compared the performances of the proposed COND mechanism with those of other systems. The number of sectors for each node is fixed at 4, and we call a round of sensing is completed when a node is switched to all of its sectors for neighbor discovery. Each time frame contains 25 slots and each slot has 4 mini-slots.

The graph of Fig. 6 a shows that the discovery latency increases with the growing number of nodes in all the studied systems. However, the rate of increase in our proposed COND mechanism is significantly lower than those in other two systems. This is achieved because of incorporating indirect discovery in COND and reduction of transmission collisions through randomized and controlled accesses of medium by its nodes. The graphs also depict that the latency is increased linearly in SAND with growing number of nodes as a central node manages the neighbor discovery.

Fig. 6

Impacts of number of sensor nodes on performances of the studied neighbor discovery algorithms. a Average discovery latency. b Sensing wastage of discovery slots. c Average discovery ration. d Control byte overhead

As we have fixed the number of slots in each time frame, the sensing wastage is very high for a low dense network in all the studied approaches, causing poor utilization of time slots. The wastage of slots reduces with the growing number of nodes up to approximately 600 nodes in COND due to collision and conflicts of nodes in competing environment of node discovery. The COND has the minimum wastage of slots because of allowing indirect node discovery, whereas many slots are wasted in the other algorithms especially for the lack of sector synchronization, as shown in Fig. 6 b.

The graphs in Fig. 6 c depict the discovery ratio of the neighboring nodes during the simulation period. The discovery ratio is 100% for all the proposed algorithms when the network density is low. The discovery ratio decreases with the growing number of nodes. Our in-depth look into the simulation trace files depicts that the last 10% of nodes take the longer time to discover. The COND mechanism performs better than the other two mechanisms with higher network density as the indirect discovery of COND mechanism increases the neighbor discovery ratio. In the two-way randomized protocol and SAND, the overheads are higher than that of COND because of additional control packet exchanges among nodes at random times due to collision and loss of token, as depicted in Fig. 6 d. The SAND has higher overhead among all the algorithms as it uses tokens to control and manage transmissions in the network.

Impacts of varying number of sectors

In this experiment, we allow each node to have two to six sectors. Here, the number of sensor nodes is fixed at 500 and the frame size at 25 time slots. The graphs of Fig. 7 a depict that the discovery latencies of the evaluated algorithms decrease with growing number of sectors from two to four. This result is achieved due to increased spatial reusability with higher number of sectors. However, our COND mechanism achieves minimum latency, and it becomes stable gradually. On the contrary, in other mechanisms, the latency increases again with beamforming angle less than 90°. The reason is that, in this situation, nodes need longer period to discover their neighbors as synchronization of antenna beams is quite challenging for narrow beam widths. For the same reason, the wastage of time slots is also minimum in COND compared to the other mechanisms, as shown in Fig. 7 b.

Fig. 7

Impacts of number of sectors on performances of the studied neighbor discovery algorithms. a Average discovery latency. b Sensing wastage of discovery slots. c Average discovery ration. d Control byte overhead

Directional antenna reduces the chance of collision among the neighboring nodes. The Fig. 7 c shows that the neighbor discovery ratio gradually increases with increasing sectors in all the mechanisms, which is as expected theoretically. Nevertheless, excessive reduction of sensing angle reduces the chance of direction synchronization among nodes, and thus, it decreases the neighbor discovery ratio. Yet again, higher number of sectors causes the nodes to switch from one sector to another frequently, resulting in transmission of more HELLO/REPLY messages. Hence, the control byte overhead is increased with the growing number of sectors, as shown in Fig. 7 d. Our COND mechanism outperforms the state-of-the-art mechanisms as it needs less control byte overheads.

Impacts of varying number of time slots

The number of time slots per round are varied from 10 to 40 for the simulation. Here, we assume fixed number of 500 sensor nodes and each node has 4 sensing sectors.

The graphs of Fig. 8 a show that the average latency for all the mechanisms decrease progressively with the growing number of time slots as each node gets longer time to discover its neighbors in each sector. The COND utilizes the time slots more efficiently and has the minimum latency by the way of indirect neighbor discovery. But unfortunately, with the growing number of slots, the sensing wastage increases as shown in Fig. 8 b. As the number of nodes are fixed at 500 and there are many time slots for neighbor discovery, the wastage increases. For the same reason, the neighbor discovery ratio increases with the growing number of time slots. However, when the number of slots are greater than 25, it becomes stable as large number of time slots are not required for neighbor discovery in a low dense network. The COND has maximum discovery ratio compared to the other systems, as shown in Fig. 8 c. The control byte overhead also decreases with the growing number of slots as the discovery ratio increases, as shown in Fig. 8 d. It increases slightly when the number of time slots crosses 30 since the possibility of using unnecessary slots is increased.

Fig. 8

Impacts of number of time slots in a frame on performances of the studied neighbor discovery algorithms. a Average discovery latency. b Sensing wastage of discovery slots. c Average discovery ration. d Control byte overhead

Average energy cost for neighbor discovery

In the last set of simulation experiments, we measure the energy consumption for varying number of nodes and sectors. The graphs of Fig. 9 show that the average energy cost per neighbor discovery increases with the growing number of nodes and sectors in all the studied systems. As the neighbor discovery rate decreases with the growing number of nodes, the energy cost increases. However, the energy cost in our proposed COND mechanism is significantly lower than those in the other two systems. This result is achieved because of efficient neighbor discovery approach used in the proposed COND.

Fig. 9

Energy consumption performances of the studied algorithms. a Impact on varying number of sensors. b Impact on varying number of sectors

Conclusions

In this paper, we investigated distributed solutions to the problem of neighbor discovery in DSNs and introduced indirect neighbor discovery through collaboration among the already discovered nodes. We also introduced dynamic polling period in each sector following the number of already discovered nodes in it. The joint employment of the above strategies helped the proposed COND system to achieve excellent performances in neighbor discovery. Our in-depth look into the simulation trace files depicts that the collaboration-based indirect neighbor discovery helped to reduce the discovery latency significantly while the utilization of time slots in each frame was greatly enhanced due to the use of dynamic polling periods. The results from simulation experiments, carried out in NS-3, showed the achievements of as high as 80 and 75% performance gains in neighbor discovery latency and discovery ratio, respectively, compared to SAND, a leading work in the literature.

In the future, we shall concentrate on developing a theoretical model for analyzing delay tuning parameter and study the effects of node mobility on performances of the proposed neighbor discovery mechanism.