1 Introduction

Compressed sensing, or compressive sampling, was proposed by David Donoho, Emmanuel Candès, Terence Tao, and Justin Romberg in the early twenty-first century. Compressed sensing started the revolution in sampling theorem and had got breakthrough applications in image compression, magnetic resonance imaging (MRI), super-broadband communication.

For signal parameter estimation, the source number is usually limited and the channel is sparse. Due to sparsity, compressed sensing (CS) can improve the performance for signal parameters estimation, including time delay, frequency, direction, and multiple parameters. In 2002, Cotter [1] proposed time delay estimation method for sparse channel by matching pursuit. Considering orthogonality, Karabulut [2] used orthogonal matching pursuit (OMP) to improved convergence speed and accuracy. Addressing the joint estimation issue, Doppler frequency and time delay were estimated by OMP and basis pursuit (BP) algorithms [3]. In [3], Beger also compared compressed sensing methods with subspace methods, such as MUSIC and ESPRIT, and the former outperformed the latter over realistic underwater acoustic channels. For direction estimation, Malioutov explored second-order cone programming to solve ℓ1 norm problem and obtained signal’s directions. Combined ℓ1 norm and ℓ2 norm by exploiting orthogonality between the noise-subspace and the overcomplete basis matrix, Zheng [4] proposed a weighted ℓ1,2-SVD (singular value decomposition) method to get more sparse solution for direction. Based on the likelihood ratio test with a sparsity promoting prior, ref [5] and [6] jointly detect the unknown number of noise-like jammers and angles of arrival. Analogously, the methods in [4–7] can also be used to estimate time delay and frequency after signal sparse reconstruction.

Signal parameters estimation by compressed sensing can achieve more excellent resolution than conventional methods such as generalized cross correlation methods [8], WRELAX (weight Fourier transform and relaxation) [9] methods and subspace methods such as MUSIC [10, 11]. But there are still some current problems: how to construct the overcomplete basis matrix when the true parameters are not in the finite set; the computation quantity is too large for high dimension scenario; moreover, the algorithms performance would be degraded severely in low SNR. Got inspired from image processing, Yang [12] suggested a deconvolved method to estimate direction, which also belonged to CS methods and obtained gain by beamforming. The method reconstructed sparse model in beam domain and could achieve better performance in low SNR. Convolution and deconvolution are common operations for image processing. Richardson and Lucy [13] proposed a classical deconvolution method, Richardson-Lucy deconvolution. These methods [14, 15] restore a blurred image to a clear one by deconvolution.

As insights from the operation, time delay estimation may obtain gain from the matched filter. Matched filter is an indispensable step for active sonar, radar, and communication. Many conventional algorithms take advantage of the cross-relation between the transmitted signal and the received signal. Ideally, the peaks should appear in the points that are corresponding to the true time delays, and matched filter or correlation methods are usually used to estimate wideband signal’s time delay. However, for narrowband signal, the matched filter output or correlation function is flat and difficult to search the peak especially for two close echoes. An ideal matched filter output is expected that nonzeros only being according to the time delays. According to the sparsity of the ideal matched filter output, or correlation function, a deconvolved method is suggested in this paper. Simulation results are provided to compare the methods based on the sparsity of channel impulse and matched filter output, and the new method has better performance in low SNR.

2 Signal model

Assume a single receiver, the received signal is

$$ x(t)= \sum_{i=1}^{K} a_{i} s(t-t_{i})+n(t),0< t<T, $$
(1)

where s(t) is the emitted source signal, T is the observation time and should be larger than s(t)’s time duration. n(t) is Gaussian white noise. The received signal x(t) is modeled by a sum of K echoes from multiple paths, with different time delay ti and amplitude variation ai. When the targets are nearly immobile, Doppler shifts can be ignored. Otherwise, Eq. (1) should be written as,

$$ x(t)= \sum_{i=1}^{K} a_{i} s(\xi_{i}(t-t_{i}))+n(t). $$
(2)

where ξi is Doppler scale, \(\xi _{i} = \frac {c+v_{i}}{c-v_{i}} \), and vi is the ith echo’s radial velocity to the platform (to be positive when closer). Usually, the velocity is far less than acoustic speed c, and \(\xi _{i} \approx 1+\frac {2v_{i}}{c}\). If narrowband hypothesis is satisfied, BT≪c/(2vi), where B is bandwidth, Doppler frequency Δfi can take place of Doppler scale. Doppler frequency shift Δfi=(ξi−1)fc and fc is carrier frequency. Under the condition, Eq. (2) can be simplified as: \(x(t)= \sum _{i=1}^{K} a_{i} s(t-t_{i})\exp (j 2\pi \Delta f_{i} t)+n(t)\). Otherwise, the duration compression cannot be ignored.

3 Methods

3.1 Previous method by channel estimation

In order to estimate time delay, some researchers have suggested to solve the problem by CS methods. Most of the methods are based on sparse channel impulse response estimation. In [16], the observed signal is considered as a convolution of the transmitted signal and channel impulse response.

$$ x(t)=s(t) \otimes h(t)+n(t), $$
(3)

where the channel impulse response h(t) includes all of the paths: \(h(t)=\sum _{i}^{K} a_{i}\delta (t-t_{i}) \). With a sampling period Ts and N samples, Eq. (1) can be written as discrete form:

$$ x(k)= \sum_{i=1}^{K} a_{i} s(k-\tau_{i})+n(k),n=0,1,\dots,N-1, $$
(4)

where \(x(k)=x(t)|_{t=k/f_{s}}, \tau _{i} = t_{i}/f_{s}\). The sampling error is ignored, and the true time delay must be contained in the set {0,Ts,(N−1)Ts}. Due to Doppler effect, the received signal’s pulse would be different from the transmitted signal’s. And it cannot be ignored for wideband signal or larger Doppler scale. As a result, in order to cover the pulse variation, N should be larger than the maximum time delay plus duration. Then, the observed signal can be rewritten as cyclic convolution form.

$$ \boldsymbol{x} = \boldsymbol{S} \boldsymbol{h}+ \boldsymbol{n} $$
(5)

where \(\boldsymbol {x}=[x(0) \quad \dots \quad x((N-1)T_{s})]\). The cyclic convolution matrix is constructed as 6.

$$ \boldsymbol{S} = \left[\begin{array}{cccc} s(0) & 0 & \dots & 0\\ s(T_{s}) & s(0) & \ddots & \vdots \\ \vdots & \vdots & \dots & 0\\ s((N-1)T_{s}) & s((N-2)T_{s}) & \dots & s((N-N_{t})T_{s}) \end{array}\right] $$
(6)

In time domain, the number of paths is much smaller than that of time samples. As a result, a sparsity representation of signal is obtained as Eq. (5). The channel impulse should be sparse and estimated by solving the ℓ0-norm problem:

$$ \min_{{\boldsymbol{h}}} \|\boldsymbol{x} - {\boldsymbol{S}} {\boldsymbol{h}}\|^{2}+ \lambda \| {\boldsymbol{h}}\|_{0} $$
(7)

ℓ0-norm counts the number of the vector’s nonzero components. The other form of ℓ0-norm minimization is K-sparse approximation,

$$ \min_{{\boldsymbol{h}}} \|\boldsymbol{x} - {\boldsymbol{S}} {\boldsymbol{h}}\|^{2}, s.t. \| {\boldsymbol{h}}\|_{0} \leq K $$
(8)

In [16], we suggested to estimate time delays by relaxing ℓ0-norm problem, including greedy algorithm and ℓ1-norm problem by convex optimization. The compressed sensing methods achieved super resolution. However, some pseudo-peaks exist and the performance would degrade severely in low SNR scenario.

3.2 1D estimation for time delay

Matched filter(MF) is a necessary operation in radar/sonar area to improve SNR. Furthermore, it is also the most conventional method for time delay estimation. The targets’ time delays can be estimated by searching the peaks of matched filter (MF) output or cross-correlation function. Definite y(τ) to be “matched filter spectrum,” as the output for matched filter in time domain:

$$ y(\tau)= \left\|\int x(t) s^{*}(t-\tau) dt\right\|^{2}, $$
(9)

where (∗) is complex conjugate symbol. When τ=ti, the output y(τ) will reach maximum. The discrete form is:

$$ y (m)= \left\|\frac{1}{N}\sum_{k=0}^{N-1}s^{*}(k-m)x(k)\right\|^{2},m=0,1,\dots,N-1. $$
(10)

and \(\boldsymbol {y} = [y(0), y(1),\dots,y(N-1)]^{\text T}\).

The resolving probability of time delay by MF depends on waveform’s Rayleigh restriction. For continuous wave (CW), the resolving probability of time delay is 0.6T, while for linear frequency modulated wave (LFM), it is 0.88/B. The MF output cannot distinguish the multipath components that are closer than the resolution limit.

Different from the channel estimation by CS, another sparsity presentation could be gotten after matched filter. For the ideal scenario that only one echo with time delay q∗Ts is received and the noise is absent, the square of MF output should be \( y_{q}(m)= \| \frac {1}{N} \sum _{k=0}^{N-1} s^{*}(k-m) s(k-q)\|^{2},m=0,1,\dots,N-1\). Note y(m,q)=yq(m),Yq is the square vector of the single echo’s MF output, \({\boldsymbol {Y}_{q}}= [y_{(0,q)}, y_{(1,q)}, \dots,y_{(N-1,q)}]^{\text T}\). In order to eliminate the impact of amplitude variation, normalized is suggested here, Cq=Yq/∥Yq∥1.

In the time delay set of \( \mathrm {T}=\{0,T_{s},\dots,(N-1)T_{s}\}\), a “matched filter spectrum” matrix is obtained, \(\boldsymbol {C}= [{\boldsymbol {C}}_{0}, {\boldsymbol {C}}_{1}, \dots,{\boldsymbol {C}}_{(N-1)}] \). \(\boldsymbol {C} \in \mathbb {C}^{N\times N}\). Hence, if the ideal echo’s time delay is in the time delay set, the square vector of the single echo’s MF output must be one of the matrix C’s column vector. Considering the amplitude variation, \(\boldsymbol {y} = \sigma _{1}^{2} \boldsymbol {C} \boldsymbol {e}_{q}\). eq is a unit vector that the qth element is 1 and the others are zero, \(\boldsymbol {e}_{q}=[0,0\dots,1, \dots,o]^{\text T}\).

For the signal as Eq. (4), the square vector of the MF output should be the sum of some weighted column vector.

$$ \boldsymbol{y} = \boldsymbol{C} \hat{\boldsymbol{y}}, $$
(11)

where \( \hat { \boldsymbol {y}} = [\hat y(0),\hat y(1)\dots,\hat y(N-1)]^{\text T}\), and \(\hat y(m) = \sum _{i=1}^{K}a_{i}^{2}\delta (m-\tau _{i})\). Therefore, \( \hat { \boldsymbol {y}}\) is a sparse vector. Accordingly, another sparsity representation is obtained as Eq. (11). C is the dictionary matrix.

The computation quantity can be cut down by pre-estimation. For instance, the echoes’ time delays can be restricted in the duration [0,Nt−1] by priori knowledge. Hence, the dimension of C is reduced to Nt×Nt, while \(\boldsymbol {S} \in \mathbb {C}^{N\times N_{t}}\).

3.3 2D estimation for time delay and Doppler

Considering the Doppler scale, a 2-dimension estimation is needed. The finite set of 2-D parameter (τ,ξ) is defined as

$$\begin{array}{@{}rcl@{}} \tau & \in &\{0, T_{s}, (N_{t}-1)T_{s} \}, \\ \xi & \in &\{\xi_{0}, \xi_{0}+\Delta \xi,\dots, \xi_{0}(N_{d}-1)\Delta \xi \}, \end{array} $$
(12)

where ξ is Doppler scale, and ξ0 is the possible minimum, Δξ is the step.

In [16], the channel impulse response h(t,ξ) on the Doppler-time plane can be formulated as:

$$ h(t,\xi)= \sum_{i=1}^{K} a_{i} \delta(t-\tau_{i})\delta(\xi-\xi_{i})\\ = \begin{array}{ll} a_{i},& t=\tau_{i}, \text {and} \xi=\xi_{i}\\ 0,& \text{else} \end{array} $$
(13)

Then, the 2D channel impulse \(\hat {\boldsymbol {h}}\) can be estimated by compressed sensing, and

$$ \min_{\hat {\boldsymbol{h}}} \|\boldsymbol{x} - \hat {\boldsymbol{S}}\hat {\boldsymbol{h}}\|^{2}+ \lambda \|\hat {\boldsymbol{h}}\|_{0} $$
(14)

The dictionary matrix \(\hat {\boldsymbol {S}}\) is expanded to a N×(NtNd) matrix, \(\hat {\boldsymbol {S}}=[\boldsymbol {S}_{1} \quad \dots \quad \boldsymbol {S}_{N_{d}}]\), where

$$ \boldsymbol{S}_{i}=\left[\begin{array}{cccc} s(0) & 0 & \dots & 0\\ s(\xi_{i} T_{s}) & s(0) & \ddots & \vdots \\ \vdots & \vdots & \dots & 0\\ s(\xi_{i} (N-1)T_{s}) & s(\xi_{i} (N-2)T_{s}) & \dots & s(\xi_{i}(N-N_{t})T_{s}) \end{array}\right] $$
(15)

The 2D channel estimation by CS has similar problem as 1-dimension (1D) estimation in low SNR. Similar to the deconvolution of matched filter output, the deconvolution on the Doppler-time plane could be expanded by a generalized matched filter or ambiguity function. The generalized matched filter output is:

$$ y(\tau,\xi)= \left\| { \int s^{*}[\xi (t-\tau)] x(t)} dt \right \|^{2}, $$
(16)

Ideally, we suppose the true time delays and Doppler scales are in the set of 2-D parameter as Eq. (12). Naturally, time delay and Doppler scale can be estimated jointly by deconvolution, which can be also achieved by compressed sensing. The dictionary matrix must be expanded to high dimension, \(\hat {\boldsymbol {C}}=[{\boldsymbol {Y}_{0,0}}, {\boldsymbol {Y}_{1,0}}, \dots, {\boldsymbol {Y}_{N_{t}-1,0}},{\boldsymbol {Y}_{0,1}},\dots, {\boldsymbol {Y}_{N_{t}-1,N_{d}-1}} ]\). Yq,p is the generalized matched filter output vector when x(t)=s(ξp(t−τq)). Hence, \(\hat {\boldsymbol {C}} \in \mathbb {C}^{(N_{d}*N_{t})\times (N_{d}*N_{t})}\), while \(\hat {\boldsymbol {S}}\in \mathbb {C}^{N\times (N_{d}*N_{t})}\).

After sparsity presentation is accomplished through channel impulse or generalized matched filter output, joint time delay and Doppler can be estimated by solving ℓ0 norm optimization problem. In order to seeking solutions to NP (nondeterministic polynominal) hard problem, there are three categories of approaches, including optimization methods based on relaxation, greedy algorithms, or Bayesian methods. The methods by using convex optimization have stable calculation accuracy but large computation quantity. Furthermore, it is difficult to choose the relax factor. MFCUSS (multiple focal underdetermined system solver) in [17] solves an underdetermined system of equations and obtains similar precision as convex method. Greedy algorithms, such as basis pursuit, matching pursuit [1], and orthogonal matching pursuit [18], can get faster computation speed but lower resolving power. Based on the statistical properties of received signal, such as Laplace prior [19] or Gaussian prior [20], sparse Bayesian methods can complement ℓ0 problem by linear programming or greedy algorithms. Without the need for sparsity in iterative process, Bayesian methods have better universality, but higher computation complexity.

4 Result and discussion

To demonstrate the algorithm, 1D and 2D estimation simulation are both designed. The CS methods based on channel impulse response and matched filter output(generalized matched filter output) are illustrated and compared.

4.1 1D estimation for time delay

Considering the target stable. The transmitted signal is CW signal and has duration T = 200 with normalized sampling frequency; the center frequency is 0.2. The received signal length is 300, composed of two echoes with time delays as 40 and 45. When SNR = 5dB, the time delays are estimated by channel impulse presentation and MF presentation as in Figs. 1 and 2. In the numerical simulation, time delays are estimated by several CS tools that have been introduced in the last section, including orthogonal matching pursuit [21] (GOMP), optimization method based on relaxation [22] (SDP), and sparse Bayesian learning [23] (SBL). The methods with sparsity representation for matched filter output are short as MF-domain methods, and a subscript “ mf” will be used to identify the methods. Meanwhile, the methods with sparsity representation for channel impulse response are short as time-domain methods (Fig. 3).

Fig. 1
figure 1

Time delay estimation in time-domain

Full size image
Fig. 2
figure 2

Time delay estimation in MF-domain

Full size image
Fig. 3
figure 3

Resolution probability by different methods vs. SNR

Full size image

Comparative values of various methods of computation time is as demonstrated in Table 1. SNR is set as 18 dB to ensure the two echoes can be distinguished, and average computation time is obtained through 200 times simulations. Optimization methods based on relaxation (SDP) are solved by quadratic programming, and get similar computation time. Other than that, the computation time of MF-domain methods are smaller than those of time-domain methods. The advantage is due to the smaller dimension of dictionary matrix in MF-domain methods.

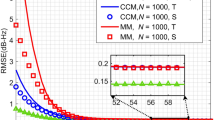
Table 1 Computation time of the methods
Full size table

Change SNR to observe different probability. τ1 and τ2 are the true time delays, while \(\hat {\tau }_{1}\) and \(\hat {\tau }_{2}\) are the estimated ones. In a single trial, if \(|\hat {\tau }_{i}-\tau _{i}|\leq \zeta \), and \(|{\hat {\tau }_{1}-\tau _{1}}| +|{\hat {\tau }_{2}-\tau _{2}}| <|{\hat {\tau }_{1}-\hat {\tau }_{2}}| \), we consider the two echoes are distinguished successfully; otherwise, they are distinguished unsuccessfully. ζ denotes error threshold to determine weather the echo estimated exactly, and it should be a small positive. It is set as 1 herein. Nest experiments are done and Nsucess ones are successful. Then, Nsucess/Nest is resolution probability. For different SNRs, 200 times Monte Carlo simulation are operated to get resolution probability as in Fig. 4a. SBL gains the optimal resolution especially by MF-domain method. In fact, evidently, resolution probabilities of MF-domain methods are all better than those of the corresponding time-domain methods, especially in the scenario of low SNR. SBL requires largest computation quantity, and the convergence index must be set properly. Otherwise, some convergence problem may be occurred. GOMP is an iterative method with the minimal computation requirement, and the resolution is worst. SDP’s performance is between the two.

Fig. 4
figure 4

Resolution probabilities by different methods vs. SNR

Full size image

The result in Fig. 4a is in scenario of CW signal. More illustration will be analyzed for LFM signal. For matched filter, large bandwidth would improve the resolving ability deservedly. Simulated results demonstrate that the methods will also get gain from bandwidth both in time domain and MF domain. Illustrated in Fig. 4b, c, and d, the normalized bandwidth are 0.05, 0.1, and 0.2 respectively. The resolution probability is increased with the bandwidth.

4.2 2D estimation for time delay and Doppler

Considering the Doppler scale, the 2D estimation are shown in this subsection. The simulation conditions are listed in Table 2.

Table 2 Directions and SNR of the signals
Full size table

The super resolution estimations are obtained after sparsity representation in Figs. 5 and 6, when the transmitted pulses are CW and LFM respectively. SNR is set as 5 dB, and both of the methods can separate the two echoes in the two simulations. Moreover, MF-domain method gives more “clear” results than time-domain method as shown in the two figures.

Fig. 5
figure 5

2D estimation for CW

Full size image
Fig. 6
figure 6

2d estimation for LFM

Full size image

5 Conclusion

In this paper, time delay estimation by compressed sensing has been studied. Besides the sparsity representation for channel impulse response, a novel sparsity representation for the matched filter output or correlation function is proposed. According to the matched filter output deconvolution, super resolution results would be obtained. For joint Doppler shift and time delay estimation, the method could be expanded by the generalized matched filter or ambiguity function. Compared to the channel sparsity representation, our method has better performance especially in low SNR scenario and smaller computation quantity for 1D estimation.