Application of the Exp-function method for solving the combined KdV-mKdV and Gardner-KP equations

Abstract

Purpose

In this article, we establish the exact solutions for the combined KdV-mKdV and Gardner-KP equations.

Methods

The Exp-function method (EFM) is used to construct solitary and soliton solutions of nonlinear evolution equations.

Results

This method is developed for searching the exact travelling wave solutions of nonlinear partial differential equations.

Conclusions

It is shown that the EFM, with the help of symbolic computation, provides a straightforward and powerful mathematical tool for solving nonlinear evolution equations in mathematical physics.

Introduction

In the recent decade, the study of nonlinear partial differential equations in modelling physical phenomena has become an important tool. Nonlinear phenomena play a fundamental role in applied mathematics and physics. Also, the investigation of the travelling wave solutions plays an important role in nonlinear sciences. A variety of powerful methods has been presented, such as the inverse scattering transform [1], Hirota’s bilinear method [2], sine-cosine method [3], homotopy perturbation method [4], homotopy analysis method [5, 6], variational iteration method [7, 8], tanh-function method [9, 10], Bäcklund transformation [11], and $\left(\frac{G^{\prime }}{G}\right)$-expansion method [12, 13]. Here we use an effective method for constructing a range of exact solutions for the following nonlinear partial differential equations which was first presented by He [14]. A new method called the Exp-function method (EFM) is presented to look for travelling wave solutions of nonlinear evolution equations. The EFM has successfully been applied to many situations. For example, He and Wu [15] have solved the nonlinear wave equations by EFM. He and Abdou [16] have used EFM to give new periodic solutions for nonlinear evolution equations. By applying EFM, generalized solitary solution and compacton-like solution of the Jaulent-Miodek equations have been obtained by He [17]. Abdou [18] has solved the generalized solitonary and periodic solutions for nonlinear partial differential equations by EFM. Manafian and Bagheri [19] have applied EFM for the modified KdV and the generalized KdV equations. Authors of [20] have studied the periodic solutions and compacton-like solutions using EFM. The EFM has been applied to nonlinear equations by Wu and He [21]. Zhu [22] also examined the hybrid-lattice system by using EFM. The EFM has recently been used by Zhang [23] in the high-dimensional nonlinear evolution equation. The positive and negative models of the Gardner equation [24, 25], or the combined KdV-mKdV equations, are given by

$$u_t+6u{u}_x\pm 6u^2{u}_x+u_{\mathit{\text{xxx}}}=0,$$

(1.1)

which describe internal solitary waves in shallow seas. Those two models will be classified as positive Gardner equation and negative Gardner equation depending on the sign of the cubic nonlinear term. The Gardner equation (Equation 1.1), like the KdV and the mKdV equation, is completely integrable with a Lax pair and inverse scattering transform [26]. Kadomtsov and Petviashivilli extended the KdV equation to obtain the Kadomtsov-Petviashivilli (KP) equation

$${(u_t+6u{u}_x+u_{\mathit{\text{xxx}}})}_x+u_{\mathit{\text{yy}}}=0.$$

(1.2)

Kadomtsov and Petviashivilli relaxed the restriction that the waves be strictly one-dimensional [26], namely, the x-direction of the KdV equation, to derive the completely integrable KP in Equation 1.2. In this article, we used EFM to investigate the Gardner-KP (GKP) equations [26] given by

$${(u_t+6u{u}_x\pm 6u^2{u}_x+u_{\mathit{\text{xxx}}})}_x+u_{\mathit{\text{yy}}}=0$$

(1.3)

that will be shown to be completely integrable. We want to obtain the analytical solutions of nonlinear combined KdV-mKdV and GKP equations and to determine the accuracy of the EFM in solving these kinds of problems. The article is organized as follows: in the section ‘Basic idea of Exp-function method’, first we briefly give the steps of the method and apply the method to solve nonlinear partial differential equations; in sections ‘The combined KdV-mKdV equations’ and ‘The Gardner-KP equations’, we examine the combined KdV-mKdV equations and the GKP equations, respectively; and a conclusion is given in the ‘Conclusions’ section.

Methods

Basic idea of Exp-function method

We first consider the nonlinear equation of the form

$$\mathcal{N}(u,u_t,u_x,u_{\mathit{\text{xx}}},,u_{\mathit{\text{yy}}},u_{\mathit{\text{tt}}},u_{\mathit{\text{tx}}},u_{\mathit{\text{ty}}},\mathrm{..})=0,$$

(2.1)

and introduce the transformation

$$u(x,y,t)=u(\eta ),\eta =x+y-\mathit{\text{ct}},$$

(2.2)

where c is constant to be determined later. Therefore Equation 2.1 is reduced to an ordinary differential equation (ODE) as

$$\mathcal{M}(u,-c{u}^{\prime },u^{\prime },u^{\prime \prime },u^{\prime \prime },\dots )=0.$$

(2.3)

EFM is based on the assumption that the travelling wave solutions in [15] can be expressed in the form

$$u(\eta )=\frac{{\sum }_{n=-c}^d{a}_n\text{exp}(n\eta )}{{\sum }_{m=-p}^q{b}_m\text{exp}(m\eta )},$$

(2.4)

where c, d, p, and q are positive integers which could be freely chosen, a _n and b _m are unknown constants to be determined. To determine the values of c and p, we balance the linear term of highest order in Equation 2.3 with the highest-order nonlinear term. Also, to determine the values of d and q, we balance the linear term of lowest order in Equation 2.3 with the lowest-order nonlinear term.

The combined KdV-mKdV equations

In this section, we employ the Exp-function method to the combined KdV-mKdV equation

$$u_t+6u{u}_x\pm 6u^2{u}_x+u_{\mathit{\text{xxx}}}=0$$

(3.1)

and we use the transformation $u=v\mp \frac{1}{2}$ to convert the model 3.1 into the modified KdV equations as

$$v_t\mp \frac{3}{2}{v}_x\pm 6v^2{v}_x+v_{\mathit{\text{xxx}}}=0.$$

(3.2)

This shows that the Gardner equation, like the modified KdV equation, is completely integrable. The Gardner equation was first derived rigorously within the asymptotic theory for long internal waves in a two-layer fluid with a density jump at the interface. The competition among dispersion, quadratic, and cubic nonlinearities constitutes the main interest of this equation [26]. The Gardner equation has been investigated in the literature because it is used to model a variety of nonlinear phenomena.

Case 1: positive Gardner equation

We use the equation

$$u_t+6u{u}_x+6u^2{u}_x+u_{\mathit{\text{xxx}}}=0,$$

(3.3)

and we use transformation

$$u=v-\frac{1}{2}$$

(3.4)

to convert the model 3.3 into the modified KdV equation of

$$v_t-\frac{3}{2}{v}_x+6v^2{v}_x+v_{\mathit{\text{xxx}}}=0,$$

(3.5)

and by using the wave variable η = x − ct reduces it to an ODE

$$-\left(c+\frac{3}{2}\right)v+2v^3+v^{\prime \prime }=0,$$

(3.6)

in which Equation 3.6 is obtained by integrating and neglecting the constant of integration. In order to the determine values of c and p, we balance the linear term of the highest order v^′′ with the highest order nonlinear term v³ in Equation 3.6 to get

$$v^{\prime \prime }=\frac{c_1\text{exp}\left(\right(c+3p)\eta )+\dots }{c_2\text{exp}(4p\eta )+\dots }$$

(3.7)

and

$$v^3=\frac{c_3\text{exp}(3c\eta )+\dots }{c_4\text{exp}(3p\eta )+\dots }=\frac{c_3\text{exp}\left(\right(3c+p)\eta )+\dots }{c_4\text{exp}(4p\eta )+\dots },$$

(3.8)

respectively. Balancing the highest order of the Exp-function in 3.7 and 3.8 and getting c + 3p = 3c + p lead to the result of c = p. Similarly, to determine the values of d and q for the terms v^′′and v³ in Equation 3.6 by simple calculation, we obtain

$$v^{\prime \prime }=\frac{\dots +d_1\text{exp}(-(d+3q)\eta )}{\dots +d_2\text{exp}(-4q\eta )}$$

(3.9)

and

$$v^3=\frac{\dots +d_3\text{exp}(-3d\eta )}{\dots +d_4\text{exp}(-3q\eta )}=\frac{\dots +d_3\text{exp}(-(3d+q)\eta )}{\dots +d_4\text{exp}(-4q\eta )},$$

(3.10)

respectively. By balancing the highest order of EFM in 3.9 and 3.10 gives us −(d + 3q) = − (3d + q), which leads to the result d = q. For simplicity, we set p = c = 1 and d = q = 1. Then Equation 2.4 reduces to

$$v(\eta )=\frac{a_1\text{exp}(\eta )+a_0+a_{-1}\text{exp}(-\eta )}{b_1\text{exp}(\eta )+b_0+b_{-1}\text{exp}(-\eta )}.$$

(3.11)

By substituting Equation 3.11 into Equation 3.6 and by using the well-known Maple software, we will have

$$\begin{array}{ll}\frac{1}{A}\left[C_3\text{exp}(3\eta )\right.& +C_2\text{exp}(2\eta )+C_1\text{exp}(\eta )+C_0+C_{-1}\text{exp}(-\eta )\\ +\left.C_{-2}\text{exp}(-2\eta )+C_{-3}\text{exp}(-3\eta )\right]=0,\end{array}$$

(3.12)

where

$$A={\left[b_{-1}\text{exp}\right(-\eta )+b_0+b_1\text{exp}(\eta \left)\right]}^3,$$

(3.13)

and C _n s are coefficients of exp(nη)s. By equating the coefficients of exp(nη) to zero, we obtain the following set of algebraic equations for a₁,a₀,a₋₁,b₁,b₀,b₋₁, and c, as

$$\left\{\begin{array}{l}{C}_3=0,C_2=0,C_1=0,\\ C_0=0,\\ C_{-3}=0,C_{-2}=0,C_{-1}=0.\end{array}\right.$$

(3.14)

Solving this system of algebraic equations with the help of Maple gives the following sets of non-trivial solutions:

• (I) The first set is

  $$\begin{array}{l}{a}_1=0,a_{-1}=0,a_0=a_0,b_0=0,b_{-1}=b_{-1},\\ b_1=\frac{a_0^2}{4b_{-1}},c=-\frac{1}{2},\end{array}$$

  (3.15)
  $$v_1(x,t)=\frac{a_0}{b_{-1}\text{exp}(-x-\frac{1}{2}t)+\frac{a_0^2}{4b_{-1}}\text{exp}(x+\frac{1}{2}t)}.$$

  (3.16)

If we choose a₀ = 2 b_{− 1}, then by using 3.4, we would get

$$\begin{array}{l}{v}_{1,1}(x,t)=\text{sech}\left(x+\frac{1}{2}t\right),\\ u_{1,1}(x,t)=-\frac{1}{2}+\text{sech}\left(x+\frac{1}{2}t\right).\end{array}$$

(3.17)

• (II) The second set is

  $$\begin{array}{l}{a}_{-1}=\pm \frac{1}{2}i{b}_{-1},a_1=0,a_0=a_0,b_0=\pm 2i{a}_0,\\ b_{-1}=b_{-1},b_1=0,c=-2,\end{array}$$

  (3.18)
  $$v_2(x,t)=\pm \frac{i}{2}\frac{b_{-1}\text{exp}(-x-2t)\mp 2i{a}_0}{b_{-1}\text{exp}(-x-2t)\pm 2i{a}_0}.$$

  (3.19)

If we choose b₋₁ = 2i a₀, then by using 3.4, we would get

$$\begin{array}{l}{v}_{2,1}(x,t)=-\frac{i}{2}\text{tanh}\left(\frac{x+2t}{2}\right),\\ v_{2,2}(x,t)=\frac{i}{2}\text{coth}\left(\frac{x+2t}{2}\right),\end{array}$$

(3.20)

$$\begin{array}{l}{u}_{2,1}(x,t)=-\frac{1}{2}-\frac{i}{2}\text{tanh}\left(\frac{x+2t}{2}\right),\\ u_{2,2}(x,t)=-\frac{1}{2}+\frac{i}{2}\text{coth}\left(\frac{x+2t}{2}\right).\end{array}$$

(3.21)

• (III) The third set is

  $$\begin{array}{l}{a}_1=\pm i{b}_1,a_{-1}=a_{-1},a_0=0,b_0=0,b_{-1}=\pm i{a}_{-1},\\ b_1=b_1,c=-\frac{7}{2},\end{array}$$

  (3.22)
  $$v_3(x,t)=\pm i\frac{b_1\text{exp}(x-\mathit{\text{ct}})\mp i{a}_{-1}}{b_1\text{exp}(x-\mathit{\text{ct}})\pm i{a}_{-1}}.$$

  (3.23)

If we choose b₁ = i a₋₁, then by using 3.4, we would get

$$\begin{array}{l}{v}_{3,1}(x,t)=i\text{tanh}\left(x+\frac{7}{2}t\right),\\ v_{3,2}(x,t)=-i\text{coth}\left(x+\frac{7}{2}t\right),\end{array}$$

(3.24)

$$\begin{array}{l}{u}_{3,1}(x,t)=-\frac{1}{2}+i\text{tanh}\left(x+\frac{7}{2}t\right),\\ u_{3,2}(x,t)=-\frac{1}{2}-i\text{coth}\left(x+\frac{7}{2}t\right).\end{array}$$

(3.25)

• (IV) The forth set is

  $$\begin{array}{l}{a}_1=\frac{1}{16}\frac{b_0^2+4a_0^2}{a_{-1}},a_{-1}=a_{-1},a_0=a_0,\\ b_0=b_0,b_{-1}=\pm 2i{a}_{-1},c=-2,\end{array}$$

  (3.26)
  $$\begin{array}{ll}{b}_1& =\mp \frac{1}{8}\frac{b_0^2+4a_0^2}{a_{-1}}i,\\ v_5(x,t)& =\frac{a_{-1}\text{exp}(-x+\mathit{\text{ct}})+a_0+\frac{1}{16}\frac{b_0^2+4a_0^2}{a_{-1}}\text{exp}(x-\mathit{\text{ct}})}{\pm 2i{a}_{-1}\text{exp}(-x+\mathit{\text{ct}})+b_0\mp \frac{1}{8}\frac{b_0^2+4a_0^2}{a_{-1}}i\text{exp}(x-\mathit{\text{ct}})}.\end{array}$$

Notice that if $u(x,t)=v(x,t)-\frac{1}{2}$, we would have

$$\begin{array}{ll}{u}_5(x,t)& =-\frac{1}{2}\\ +\frac{a_{-1}\text{exp}(-x-2t)+a_0+\frac{1}{16}\frac{b_0^2+4a_0^2}{a_{-1}}\text{exp}(x+2t)}{\pm 2i{a}_{-1}\text{exp}(-x-2t)+b_0\mp \frac{1}{8}\frac{b_0^2+4a_0^2}{a_{-1}}i\text{exp}(x+2t)}.\end{array}$$

(3.27)

Case 2: negative Gardner equation

Let

$$u_t+6u{u}_x-6u^2{u}_x+u_{\mathit{\text{xxx}}}=0$$

(3.28)

and use the transformation

$$u=v+\frac{1}{2},$$

(3.29)

which converts the model 3.28 into the modified KdV equation

$$v_t+\frac{3}{2}{v}_x-6v^2{v}_x+v_{\mathit{\text{xxx}}}=0$$

(3.30)

and by using the wave variable η = x − ct reduces it to an ODE

$$-\left(c-\frac{3}{2}\right)v-2v^3+v^{\prime \prime }=0,$$

(3.31)

in which Equation 3.31 is obtained by integrating and neglecting the constant term of integration. By manipulating the above procedure, we get the following sets.

• (I) The first set is

  $$\begin{array}{l}{a}_1=0,a_{-1}=a_{-1},a_0=a_0,b_0=2a_0,b_{-1}=-2a_{-1},\\ b_1=0,c=1,\end{array}$$

  (3.32)
  $$v_1(x,t)=\frac{a_{-1}\text{exp}(-x+t)+a_0}{-2a_{-1}\text{exp}(-x+t)+2a_0}.$$

  (3.33)

If we choose a₀ = a₋₁, then by using 3.29, we would get

$$\begin{array}{l}{v}_{1,1}(x,t)=\frac{1}{2}\text{coth}\left(\frac{x-t}{2}\right),\\ u_{1,1}(x,t)=\frac{1}{2}+\frac{1}{2}\text{coth}\left(\frac{x-t}{2}\right).\end{array}$$

(3.34)

• (II) The second set is

  $$\begin{array}{l}{a}_{-1}=0,a_1=0,a_0=a_0,b_0=0,b_{-1}=b_{-1},\\ b_1=-\frac{1}{4}\frac{a_0^2}{b_{-1}},c=\frac{5}{2},\end{array}$$

  (3.35)
  $$\begin{array}{l}{v}_2(x,t)=\frac{a_0}{b_{-1}\text{exp}(-x+\frac{5}{2}t)-\frac{1}{4}\frac{a_0^2}{b_{-1}}\text{exp}(x-\frac{5}{2}t)}.\end{array}$$

  (3.36)

If we choose 2b₋₁ = a₀, then by using 3.29, we would get

$$\begin{array}{l}{v}_{2,1}(x,t)=-\text{csch}\left(x-\frac{5}{2}t\right),\\ u_{2,1}(x,t)=\frac{1}{2}-\text{csch}\left(x-\frac{5}{2}t\right).\end{array}$$

(3.37)

• (III) The third set is

  $$\begin{array}{l}{a}_{-1}=-\frac{1}{16}\frac{b_0^2-4a_0}{a_1},a_1=a_1,a_0=a_0,b_0=b_0,\\ b_{-1}=\mp \frac{1}{8}\frac{b_0^2-4a_0}{a_1},\end{array}$$

  (3.38)
  $$\begin{array}{ll}{b}_1& =\mp 2a_1,c=1,\\ v_3(x,t)& =\frac{-\frac{1}{16}\frac{b_0^2-4a_0}{a_1}\text{exp}(-x+t)+a_0+a_1\text{exp}(x-t)}{\mp \frac{1}{8}\frac{b_0^2-4a_0}{a_1}\text{exp}(-x+t)+b_0\mp 2a_1\text{exp}(x-t)}.\end{array}$$

Notice that if $u(x,t)=v(x,t)+\frac{1}{2}$, we would obtain

$$\begin{array}{l}{u}_3(x,t)=\frac{1}{2}+\frac{-\frac{1}{16}\frac{b_0^2-4a_0}{a_1}\text{exp}(-x+t)+a_0+a_1\text{exp}(x-t)}{\mp \frac{1}{8}\frac{b_0^2-4a_0}{a_1}\text{exp}(-x+t)+b_0\mp 2a_1\text{exp}(x-t)}.\end{array}$$

(3.39)

• (IV) The fourth set is

  $$a_1=a_1,a_{-1}=a_{-1},a_0=0,b_0=0,b_{-1}=a_{-1},c=-\frac{1}{2},$$

  (3.40)
  $$\begin{array}{l}{b}_1=-a_1,v_4(x,t)=\frac{a_{-1}\text{exp}(-x-\frac{1}{2}t)+a_1\text{exp}(x+\frac{1}{2}t)}{a_{-1}\text{exp}(-x-\frac{1}{2}t)-a_1\text{exp}(x+\frac{1}{2}t)}.\end{array}$$

If we choose a₋₁ = a₁, then by using 3.29, we would get

$$\begin{array}{l}{v}_4(x,t)=-\text{coth}\left(x+\frac{1}{2}t\right),\\ u_4(x,t)=\frac{1}{2}-\text{coth}\left(x+\frac{1}{2}t\right),\end{array}$$

(3.41)

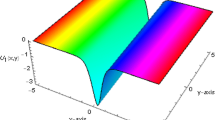
which are the exact solutions of the combined KdV-mKdV equation. We obtain solitary wave and complex wave solutions for the combined KdV-mKdV equation. It can be seen that the results are the same as the results in [26].

Results and discussion

The Gardner-KP equations

In this section, we study the Gardner-KP equations with EFM as

$${(u_t+6u{u}_x\pm 6u^2{u}_x+u_{\mathit{\text{xxx}}})}_x+u_{\mathit{\text{yy}}}=0,$$

(4.1)

and we use transformation $u=v\mp \frac{1}{2}$ to convert the model 4.1 into the Gardner-KP equation

$${(v_t\mp \frac{3}{2}{v}_x\pm 6v^2{v}_x+v_{\mathit{\text{xxx}}})}_x+v_{\mathit{\text{yy}}}=0.$$

(4.2)

This shows that the positive GKP equation is completely integrable like the modified KdV equation.

Case 1:positive Gardner-KP equation

Consider

$${(u_t+6u{u}_x+6u^2{u}_x+u_{\mathit{\text{xxx}}})}_x+u_{\mathit{\text{yy}}}=0,$$

(4.3)

and we use the transformation

$$u=v-\frac{1}{2}$$

(4.4)

to reduce to the model 4.3 into the Gardner-KP equation as

$${(v_t-\frac{3}{2}{v}_x+6v^2{v}_x+v_{\mathit{\text{xxx}}})}_x+v_{\mathit{\text{yy}}}=0$$

(4.5)

and by using the wave variable η = x + y − ct reduces it to an ODE of

$$-\left(c+\frac{1}{2}\right)v+2v^3+v^{\prime \prime }=0,$$

(4.6)

in which Equation 4.6 is obtained by integrating and neglecting the constant term of integration. In order to the determine values of c and p, we balance v^′′with v³ in Equation 4.6 to get

$$v^{\mathrm{\prime \prime }}=\frac{c_1\text{exp}\left(\right(c+3p)\eta )+\dots }{c_2\text{exp}(4p\eta )+\dots }$$

(4.7)

and

$$v^3=\frac{c_3\text{exp}(3c\eta )+\dots }{c_4\text{exp}(3p\eta )+\dots }=\frac{c_3\text{exp}\left(\right(3c+p)\eta )+\dots }{c_4\text{exp}(4p\eta )+\dots },$$

(4.8)

respectively. By balancing the highest order of EFM in 4.7 and 4.8, we will have c + 3p = 3 c + p which leads to the result c = p. Similarly, to determine values of d and q for the terms v^′′and v³ in Equation 4.6, by simple calculation we obtain

$$v^{\prime \prime }=\frac{\dots +d_1\text{exp}(-(d+3q)\eta )}{\dots +d_2\text{exp}(-4q\eta )}$$

(4.9)

and

$$\begin{array}{c}{v}^3=\frac{\dots +d_3\text{exp}(-3d\eta )}{\dots +d_4\text{exp}(-3q\eta )}=\frac{\dots +d_3\text{exp}(-(3d+q)\eta )}{\dots +d_4\text{exp}(-4q\eta )},\end{array}$$

(4.10)

respectively. By balancing the highest order of EFM in 4.9 and 4.10, we have −(d + 3q) = −(3d + q) which leads to the result d = q. Moreover, by substituting Equation 3.11 into Equation 4.6, using the well-known Maple software, and applying the same manipulation as illustrated above, we have the following set of solutions.

• (I) The first set is

  $$\begin{array}{l}{a}_1=0,a_{-1}=0,a_0=a_0,b_0=0,b_{-1}=b_{-1},\\ b_1=\frac{a_0^2}{4b_{-1}},c=\frac{1}{2},\end{array}$$

  (4.11)
  $$\begin{array}{l}{v}_1(x,y,t)=\frac{a_0}{b_{-1}\text{exp}(-x-y+\frac{1}{2}t)+\frac{a_0^2}{4b_{-1}}\text{exp}(x+y-\frac{1}{2}t)}.\end{array}$$

  (4.12)

If we choose a₀ = 2b₋₁, then by using 4.4, we would get

$$\begin{array}{l}{v}_{1,1}(x,y,t)=\text{sech}\left(x+y-\frac{1}{2}t\right),\\ u_{1,1}(x,y,t)=-\frac{1}{2}+\text{sech}\left(x+y-\frac{1}{2}t\right).\end{array}$$

(4.13)

• (II) The second set is

  $$\begin{array}{l}{a}_{-1}=\pm \frac{1}{2}i{b}_{-1},a_1=0,a_0=a_0,b_0=\pm 2i{a}_0,\\ b_{-1}=b_{-1},b_1=0,c=-1,\end{array}$$

  (4.14)
  $$v_2(x,y,t)=\pm \frac{i}{2}\frac{b_{-1}\text{exp}(-x-y-t)\mp 2i{a}_0}{b_{-1}\text{exp}(-x-y-t)\pm 2i{a}_0}.$$

  (4.15)

If we choose b_{− 1} = 2i a₀, then by using 4.4, we would get

$$\begin{array}{l}{v}_{2,1}(x,y,t)=-\frac{i}{2}\text{tanh}\left(\frac{x+y+t}{2}\right),\\ u_{2,1}(x,y,t)=-\frac{1}{2}-\frac{i}{2}\text{tanh}\left(\frac{x+y+t}{2}\right),\end{array}$$

(4.16)

$$\begin{array}{l}{v}_{2,2}(x,y,t)=\frac{i}{2}\text{coth}\left(\frac{x+y+t}{2}\right),\\ u_{2,2}(x,y,t)=-\frac{1}{2}+\frac{i}{2}\text{coth}\left(\frac{x+y+t}{2}\right).\end{array}$$

(4.17)

• (III) The third set is

  $$\begin{array}{l}{a}_1=\pm i{b}_1,a_{-1}=a_{-1},a_0=0,b_0=0,\\ b_{-1}=\pm i{a}_{-1},b_1=b_1,c=-\frac{5}{2},\end{array}$$

  (4.18)
  $$v_3(x,y,t)=\pm i\frac{b_1\text{exp}(x+y-\mathit{\text{ct}})\mp i{a}_{-1}}{b_1\text{exp}(x+y-\mathit{\text{ct}})\pm i{a}_{-1}}.$$

  (4.19)

If we choose b₁ = i a₋₁, then by using 4.4, we would get

$$\begin{array}{l}{v}_{3,1}(x,y,t)=i\text{tanh}\left(x+y+\frac{5}{2}t\right),\\ u_{3,1}(x,y,t)=-\frac{1}{2}+i\text{tanh}\left(x+y+\frac{5}{2}t\right),\end{array}$$

(4.20)

$$\begin{array}{l}{v}_{3,2}(x,y,t)=-i\text{coth}\left(x+y+\frac{5}{2}t\right),\\ u_{3,2}(x,y,t)=-\frac{1}{2}-i\text{coth}\left(x+y+\frac{5}{2}t\right).\end{array}$$

(4.21)

• (IV) The fourth set is

  $$\begin{array}{l}{a}_1=\frac{1}{16}\frac{b_0^2+4a_0^2}{a_{-1}},a_{-1}=a_{-1},a_0=a_0,b_0=b_0,\\ b_{-1}=\pm 2i{a}_{-1},c=-1,\end{array}$$

  (4.22)
  $$b_1=\mp \frac{1}{8}\frac{b_0^2+4a_0^2}{a_{-1}}i,$$
  $$\begin{array}{l}{v}_4(x,y,t)\\ =\frac{a_{-1}\text{exp}(-x-y-t)+a_0+\frac{1}{16}\frac{b_0^2+4a_0^2}{a_{-1}}\text{exp}(x+y+t)}{\pm 2i{a}_{-1}\text{exp}(-x-y-t)+b_0\mp \frac{1}{8}\frac{b_0^2+4a_0^2}{a_{-1}}i\text{exp}(x+y+t)}.\end{array}$$

Notice that $u(x,y,t)=v(x,y,t)-\frac{1}{2}$, we would have

$$\begin{array}{l}{u}_4(x,y,t)=-\frac{1}{2}\\ +\frac{a_{-1}\text{exp}(-x-y-t)+a_0+\frac{1}{16}\frac{b_0^2+4a_0^2}{a_{-1}}\text{exp}(x+y+t)}{\pm 2i{a}_{-1}\text{exp}(-x-y-t)+b_0\mp \frac{1}{8}\frac{b_0^2+4a_0^2}{a_{-1}}i\text{exp}(x+y+t)}.\end{array}$$

(4.23)

Case 2: negative Gardner-KP equation

Consider

$${(u_t+6u{u}_x-6u^2{u}_x+u_{\mathit{\text{xxx}}})}_x+u_{\mathit{\text{yy}}}=0,$$

(4.24)

and we use transformation

$$u=v+\frac{1}{2},$$

(4.25)

to convert the model 4.24 into the Gardner-KP equation

$${(v_t+\frac{3}{2}{v}_x-6v^2{v}_x+v_{\mathit{\text{xxx}}})}_x+v_{\mathit{\text{yy}}}=0$$

(4.26)

and by using the wave variable η = x + y − ct reduces it to an ODE

$$-\left(c-\frac{5}{2}\right)v-2v^3+v^{\mathrm{\prime \prime }}=0,$$

(4.27)

in which Equation 4.27 is obtained by integrating and neglecting the constant of integration. By manipulating above procedure we get the following sets.

• (I) The first set is

  $$\begin{array}{l}{a}_1=0,a_{-1}=a_{-1},a_0=a_0,b_0=2a_0,b_{-1}=-2a_{-1},\\ b_1=0,c=2,\end{array}$$

  (4.28)
  $$v_1(x,y,t)=\frac{a_{-1}\text{exp}(-x-y+\mathit{\text{ct}})+a_0}{-2a_{-1}\text{exp}(-x-y+\mathit{\text{ct}})+2a_0}.$$

  (4.29)

If we choose a₀ = a_{− 1}, then by using Equation 4.25, we would get

$$\begin{array}{l}{v}_{1,1}(x,y,t)=\frac{1}{2}\text{coth}\left(\frac{x+y-2t}{2}\right),\\ u_{1,1}(x,y,t)=\frac{1}{2}+\frac{1}{2}\text{coth}\left(\frac{x+y-2t}{2}\right).\end{array}$$

(4.30)

• (II) The second set is

  $$\begin{array}{l}{a}_{-1}=0,a_1=0,a_0=a_0,b_0=0,\\ b_{-1}=b_{-1},b_1=-\frac{1}{4}\frac{a_0^2}{b_{-1}},c=\frac{7}{2},\end{array}$$

  (4.31)
  $$\begin{array}{l}{v}_2(x,y,t)=\frac{a_0}{b_{-1}\text{exp}(-x-y+\mathit{\text{ct}})-\frac{1}{4}\frac{a_0^2}{b_{-1}}\text{exp}(x+y-\mathit{\text{ct}})}.\end{array}$$

  (4.32)

If we choose 2b₋₁ = a₀, then by using Equation 4.25, we would get

$$\begin{array}{l}{v}_{2,1}(x,y,t)=-\text{csch}\left(x+y-\frac{7}{2}t\right),\\ u_{2,1}(x,y,t)=\frac{1}{2}-\text{csch}\left(x+y-\frac{7}{2}t\right).\end{array}$$

(4.33)

• (III) The third set is

  $$\begin{array}{l}{a}_{-1}=-\frac{1}{16}\frac{b_0^2-4a_0}{a_1},a_1=a_1,a_0=a_0,b_0=b_0,\\ b_{-1}=\mp \frac{1}{8}\frac{b_0^2-4a_0}{a_1},\end{array}$$

  (4.34)
  $$b_1=\mp 2a_1,c=2,$$
  $$\begin{array}{l}{v}_3(x,y,t)\\ =\frac{-\frac{1}{16}\frac{b_0^2-4a_0}{a_1}\text{exp}(-x-y+2t)+a_0+a_1\text{exp}(x+y-2t)}{\mp \frac{1}{8}\frac{b_0^2-4a_0}{a_1}\text{exp}(-x-y+2t)+b_0\mp 2a_1\text{exp}(x+y-2t)}.\end{array}$$

  (4.35)

Notice that in $u(x,y,t)=v(x,y,t)+\frac{1}{2}$, we would obtain

$$\begin{array}{l}{u}_3(x,y,t)=\frac{1}{2}\\ +\frac{-\frac{1}{16}\frac{b_0^2-4a_0}{a_1}\text{exp}(-x-y+2t)+a_0+a_1\text{exp}(x+y-2t)}{\mp \frac{1}{8}\frac{b_0^2-4a_0}{a_1}\text{exp}(-x-y+2t)+b_0\mp 2a_1\text{exp}(x+y-2t)}.\end{array}$$

(4.36)

• (IV) The fourth set is

  $$\begin{array}{l}{a}_1=a_1,a_{-1}=a_{-1},a_0=0,b_0=0,b_{-1}=a_{-1},c=\frac{1}{2},\\ b_1=-a_1,\end{array}$$

  (4.37)
  $$\begin{array}{l}{v}_4(x,y,t)=\frac{a_{-1}\text{exp}(-x-y+\mathit{\text{ct}})+a_1\text{exp}(x+y-\mathit{\text{ct}})}{a_{-1}\text{exp}(-x-y+\mathit{\text{ct}})-a_1\text{exp}(x+y-\mathit{\text{ct}})}.\end{array}$$

  (4.38)

If we choose a₋₁ = a₁, then by using Equation 4.25, we would get

$$\begin{array}{l}{v}_4(x,y,t)=-\text{coth}\left(x+y-\frac{1}{2}t\right),\\ u_4(x,y,t)=\frac{1}{2}-\text{coth}\left(x+y-\frac{1}{2}t\right),\end{array}$$

(4.39)

which are the exact solutions of the Gardner-KP equation. We obtain solitary wave and complex wave solutions for the combined KdV-mKdV equation. It can be seen that the results are the same when compared to the results in [26].

Conclusions

In this article, we obtained the exact solutions for the combined KdV-mKdV and Gardner-KP equations by Exp-function method. EFM is a useful method for finding travelling wave solutions of nonlinear evolution equations. This method has been successfully applied to obtain some new solitary wave solutions to the combined KdV-mKdV and Gardner-KP equations. Some of these results are in agreement with the results reported in the literature. Also, new results are formally developed in this article considerably. It can be concluded that this method is a very powerful and efficient technique to find the exact solutions for a large class of problems.