Abstract
In this paper, we present a complete list of rigid spherical CR hypersurfaces in  . The construction is based on a renormalization of Stanton’s family of rigid spheres.
. The construction is based on a renormalization of Stanton’s family of rigid spheres.
Mathematics Subject Classification
32V05.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The class of real hypersurfaces in complex space that are invariant with respect to an infinitesimal translation transversal to the complex tangent space is known as rigid hypersurfaces (see [1]). In this article, we consider rigid hypersurfaces in  with coordinates z,w=u+iv. In this case, a rigid hypersurface can be locally described by an equation of the form v=h(z).
with coordinates z,w=u+iv. In this case, a rigid hypersurface can be locally described by an equation of the form v=h(z).
In 1991, Stanton [8] developed a normal form for rigid hypersurfaces. Other normal forms that reflect the presence of symmetries have been constructed by Kolář [5] and Ezhov et al. [2] more recently.
It is a natural question how to recognise hypersurfaces that are holomorphically equivalent to the model hypersurface, i.e. the sphere v=|z|2, via its normal form. As an application of the normal form, Stanton derived a list of examples of normal forms equivalent to the sphere:


where b and c=r+iθ are complex parameters. The remaining examples from Stanton’s list can be obtained by letting r and θ converge to 0. In particular, for b=0 and θ=0, one finds the pendant to (1)

Stanton has raised the question whether this list was complete. Her method was based on the analysis of the holomorphic mappings that transform the infinitesimal translation ∂/∂ w into a vector field of a seven-parameter family of infinitesimal sphere automorphisms. She acknowledged that the listed examples correspond to a four-parameter subfamily.
The main aim of this paper is to provide a complete classification of spherical rigid hypersurfaces. Combined with Stanton’s results, this also answers Rothschild’s question which rigid hypersurfaces are equivalent to a hypersurface that is given by an equation:

where p is a homogeneous polynomial (see [8]). Stanton has solved this problem for polynomials of degree bigger than two. Our result completes the case of degree 2.
The following argument gives the upper bound 4 for the number of parameters involved: In the Levi non-degenerate case, which applies for spherical rigid hypersurfaces, Stanton’s normal form is similar to Chern-Moser’s normal form, except for the terms of the defining function ϕ of bidegrees (2,2), (2,3), (3,2) and (3,3) with respect to  being allowed to be any constants. These four real constants completely control the rigid hypersurface. Thus, the normal form equation becomes:
being allowed to be any constants. These four real constants completely control the rigid hypersurface. Thus, the normal form equation becomes:

The coefficients c
22,  and c
33 depend in an algebraic way on Stanton’s parameters b and c. It can be shown that not all coefficients can be attained in this way, which indicates that Stanton’s list is incomplete. In the case when c
23=0, Stanton’s example reduces to:
and c
33 depend in an algebraic way on Stanton’s parameters b and c. It can be shown that not all coefficients can be attained in this way, which indicates that Stanton’s list is incomplete. In the case when c
23=0, Stanton’s example reduces to:

which realises only the coefficients  . The coefficients
. The coefficients  are realised by the family:
are realised by the family:

which for θ=0 coincides with (1) but was absent in Stanton’s list for θ≠0.
We show that Stanton’s mappings of a rigid sphere to the Heisenberg sphere can be modified by combining them with suitable sphere automorphisms so that all parameters can be covered.
This yields not only the desired classification but also provides the complete solution to a non-linear partial differential equation (PDE) that expresses the zero-curvature equation of a rigid hypersurface M in normal form:

It is well known that local sphericity is equivalent to vanishing of the Cartan curvature (see, e.g.[3]). For rigid hypersurfaces the zero-curvature equation simplifies to

where  . Loboda has derived and studied PDE (4) in [6]. In particular he found the solution (3). The PDE (4) appears in relation to the study of shear-free congruences of null geodesics in a Lorentzian geometry by Robinson and Wilson in [7]. In particular, they establish a correspondence between the Taub-NUT congruence and a CR manifold that is equivalent to our CR manifold sinhv=e−v|z|2.
. Loboda has derived and studied PDE (4) in [6]. In particular he found the solution (3). The PDE (4) appears in relation to the study of shear-free congruences of null geodesics in a Lorentzian geometry by Robinson and Wilson in [7]. In particular, they establish a correspondence between the Taub-NUT congruence and a CR manifold that is equivalent to our CR manifold sinhv=e−v|z|2.
2 Modified normalisation
We apply a modified Chern-Moser normalisation procedure to the Heisenberg sphere Imw 2=|z 2|2 to obtain a hypersurface of the form:

For given c 22,c 23,c 33, such normalisation mapping is uniquely determined up to automorphisms of the Heisenberg sphere. All rigid spheres can be found by this procedure, though the resulting hypersurface does not have to be rigid in the higher-order terms a priori. We construct the inverse mapping as a composition of two:

Here, we assume:

Condition (5) is imposed for convenience in computation and can be fixed at the next step.
The second mapping has the form:

Then, p,α,h satisfy the equations:



with initial conditions p(0)=0, h(0)=0, h ′(0)>0. Using combinations with automorphisms of the Heisenberg sphere we may assume that α(0)=0, h ′(0)=1, p ′(0)=0, h ′′(0)=0. It follows that, for given c 22,c 23,c 33, system (6)-(8) has unique solutions α,p,h.
Though it is easy to successively compute the coefficients of the power series of α,p,h from recursive formulae, we have not succeeded in solving this system of ODE, except for c 23=0. In this case, p≡0 and:

3 Stanton’s mapping
Rigid surfaces can be characterised by the presence of a translation symmetry transversal to the complex tangent spaces. In suitable local coordinates, such symmetry is generated as the flow of the vector field  . Stanton constructed holomorphic mappings in the ambient space that pull a suitable infinitesimal automorphism X of the Heisenberg sphere back to
. Stanton constructed holomorphic mappings in the ambient space that pull a suitable infinitesimal automorphism X of the Heisenberg sphere back to  . The relevant infinitesimal automorphisms of the Heisenberg sphere are well-known and form a seven-parametric family consisting of:
. The relevant infinitesimal automorphisms of the Heisenberg sphere are well-known and form a seven-parametric family consisting of:

where  and
and  and
and  .
.
The resulting system is:

with initial conditions  , W(z,0)≡0. Stanton solved this system in the particular case a=ρ=0, that is when (9) is linear. The solutions are:
, W(z,0)≡0. Stanton solved this system in the particular case a=ρ=0, that is when (9) is linear. The solutions are:

Substituting this mapping into the sphere equation, v=|z|2 yields (2). We show that not all values of the parameters c 22,c 23,c 33 can be realised by these mappings. Direct computation shows that the explicit sixth-order expansion of (2) is:

Hence, the parameters take the form:



Stanton’s family realises all those c
22,c
23,c
33 for which the system of algebraic equations (12)-(14) has a solution  ,
,  . A method to solve this system is to first express θ using Equation (12) then express r
2 through c
33 and |b|2 using Equation (14) and plug it into the absolute square of Equation (13). Solve the resulting cubic equation on |b|2 and finally find r,θ. However, the resulting values for |b|2 or r
2 could turn out to be negative.
. A method to solve this system is to first express θ using Equation (12) then express r
2 through c
33 and |b|2 using Equation (14) and plug it into the absolute square of Equation (13). Solve the resulting cubic equation on |b|2 and finally find r,θ. However, the resulting values for |b|2 or r
2 could turn out to be negative.
Consider two examples: 1. Let c 23=0. Then, b=0, and (14) becomes:

By allowing r 2 to become negative, the solution:

turns into (1).
-
2.
For c 22=0 and c 23=2, only c 33≥−2 is feasible. Indeed, from Equation (12), we get θ=3|b|2. Then, (13) is equivalent to:

This implies:

and hence:

This is only possible if |b|≤1. Now (14) becomes:

Finally, we point out that Stanton’s mapping can be interpreted as modified normalisation with:

Notice that the initial conditions are p ′(0)=b and h ′′(0)=−2r.
On the other hand, the proposition below shows that the solutions of (9) with different vector fields X yield the missing rigid spheres.
Proposition 1
For any set of parameters c 22,c 23,c 33, there exists a rigid sphere. It can be realised by the solutions Z(z,w),W(z,w) of (9) with parameters c=iθ,a,ρ and Re c=b=0, where:

and initial conditions Z(z,0)=z, W(z,0)=0.
Proof
For any choice of parameters c 22,c 23,c 33, we find the corresponding parameters θ,a,ρ and hence the infinitesimal sphere automorphism X. According to the Picard-Lindelöf theorem, the system (9) has a unique solution with initial conditions Z(z,0)=z, W(z,0)=0.
Direct computations with jets show that:

where the dots indicate terms of order higher than 3. Substituting these truncated mappings into the sphere equation:

yields:

where the dots indicate terms of bidegree (2,4) and (4,2) and higher order.
It is an immediate consequence that the modified Chern-Moser normalisation of the Heisenberg sphere from Section 2 yields indeed rigid hypersurfaces.
4 Twisting Stanton’s mapping
One way to produce solutions of (9) with non-trivial a,ρ is to apply the adjoint action of SU(2,1) on the coefficient matrix of the linear system in a suitable way. Geometrically, this amounts to compose Stanton’s mapping with a sphere automorphism. The composition of Stanton’s mapping z 1(z,w),w 1(z,w) with parameters c=r+iθ,b and the sphere automorphism:

is:

with:

where a=−b(r−i θ+2 i|b|2) and ϕ=|b|2.
Notice that the Taylor series of:

has coefficients a 0=a 1=0:

for n≥1 and therefore is divisible by r 2+θ 2. Clearly, sinhr w is divisible by r. Therefore, P 1,P 2,Q are entire functions with respect to z,w,r,θ,a,ϕ. Moreover, they are even functions with respect to r.
The vector field  is pulled back to:
is pulled back to:

where:

We make formula (15) universal by allowing imaginary r and negative ϕ.
Solving (16) for θ,b,r, we find:

Now ϕ can be determined from the equation:

Notice that the cubic equation has real coefficients and therefore has at least one real solution. Let ϕ be any real solution.
For τ=0, the solution ϕ can be given by the formula:

Here, we take the principal branch of the cubic root on the right half-plane and the real cubic root on the real axis. Notice that ϕ is a continuous real-valued function, though not necessarily non-negative, and that ϕ=0 for a=0.
Theorem 1
Let:

where P 1,P 2,Q are as in (15) and θ and r 2 are expressed as functions of τ,ρ,ϕ by (17).
Then, Z,W satisfy the system (9) on the real algebraic set given by (18).
It follows that all rigid spheres can be found as inverse images of ImW=|Z|2 under the mappings Z,W with suitable parameters τ,a,ρ,θ and therefore have the form:

Proof.
Direct computation shows that the expressions:

factorise with a factor 4ϕ 3+4τ ϕ 2+(τ 2−ρ)ϕ−|a|2=4ϕ 3−4θ ϕ 2+(θ 2+r 2)ϕ−|a|2.
In fact:

and:

Therefore, Z,W satisfy the system (9) on the real algebraic set (18).
Now the rigid sphere formula can be obtained either from Stanton’s formula (2) by replacing r,θ,b by their expressions in τ,a,ρ,θ or by inserting Z,W into the standard Heisenberg sphere equation.
Notice that the Taylor series of  has coefficients a
0=a
1=0:
has coefficients a
0=a
1=0:

for n≥1 and therefore is divisible by r 2+θ 2. Clearly, sin2r v is divisible by r. It follows that the rigid sphere formula is an entire function with respect to all variables and parameters.
We find an example of a rigid sphere that is not in Stanton’s family by setting:

Then:

and:

5 The zero-curvature equation
Local equivalence of a real hypersurface M in  to a sphere can be characterised by vanishing of its Cartan curvature. In [3], an explicit expression of the Cartan curvature has been computed. In the case of rigid hypersurfaces, this expression considerably simplifies. If M is given by the equation:
to a sphere can be characterised by vanishing of its Cartan curvature. In [3], an explicit expression of the Cartan curvature has been computed. In the case of rigid hypersurfaces, this expression considerably simplifies. If M is given by the equation:

vanishing of the Cartan curvature is equivalent to the non-linear PDE:

with  . The condition that h is a real function translates into
. The condition that h is a real function translates into  .
.
Notice that the normal form conditions on h are encoded in the choice of the solution of the auxiliary equation:

together with the condition that f does not contain antiholomorphic terms.
Though we did not succeed in solving the zero-curvature equation directly, we can demonstrate the special cases when M is circular, i.e. v=f(|z|2), or M is a tube, i.e. v=h(x).
In the circular case:

and the equation on g= log(t h ′′+h ′) with t replacing |z|2 is:

Formal power series solutions:

are determined by c 1,c 2. They correspond to the surfaces:

with  ,
,  and
and  respectively.
respectively.
The spherical tubes are well-known (see, for instance, [4]). They are never in rigid normal form, and they are affinely equivalent to one of the following:

This corresponds to the solutions for (19) listed below, respectively:

If follows:

which yields the tubes:

which are affinely equivalent to the tubes (20).
References
Baouendi MS, Rothschild LP, Trèves F: CR structures with group action and extendability of CR functions. Invent. Math 1985,82(2):359–396. issn: 0020–9910, doi: 10.1007/BF01388808
Ezhov V, Kolář M, Schmalz G:Normal forms and symmetries of real hypersurfaces of finite type in
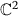 . Indiana Univ. Math. J 2013,62(1):1–32. 10.1512/iumj.2013.62.4833
. Indiana Univ. Math. J 2013,62(1):1–32. 10.1512/iumj.2013.62.4833Ezhov V, McLaughlin B, Schmalz G: From Cartan to Tanaka: getting real in the complex world. Notices Amer. Math. Soc 58(1):20–27. issn: 0002–9920
Isaev A: Spherical tube hypersurfacesLecture Notes in Mathematics, vol. 2020. Heidelberg: Springer; 2011. pp. xii+220, isbn=978–3-642–19782–6, doi: 10.1007/978–3-642–19783–3
Kolář M:Local equivalence of symmetric hypersurfaces in
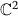 . Trans. Amer. Math. Soc 2010,362(6):2833–2843. issn: 0002–9947, doi: 10.1090/S0002–9947–10–05058–0
. Trans. Amer. Math. Soc 2010,362(6):2833–2843. issn: 0002–9947, doi: 10.1090/S0002–9947–10–05058–0Loboda AV:On the sphericity of rigid hypersurfaces in
 . Mat. Zametki 1997,62(3):391–403. issn:0025–567X, English translation in Math. Notes, 62(3–4), 329–338 (1998), issn:0001–4346, doi:10.1007/BF02360874 issn:0025-567X, English translation in Math. Notes, 62(3–4), 329–338 (1998)
. Mat. Zametki 1997,62(3):391–403. issn:0025–567X, English translation in Math. Notes, 62(3–4), 329–338 (1998), issn:0001–4346, doi:10.1007/BF02360874 issn:0025-567X, English translation in Math. Notes, 62(3–4), 329–338 (1998)Robinson I, Wilson EP: The generalized Taub-NUT congruence in Minkowski space. Gen. Relativity Gravit 1993,25(3):225–244. issn: 0001–7701, doi: 10.1007/BF00756258
Stanton NK: A normal form for rigid hypersurfaces in C 2 . Amer. J. Math 1991,113(5):877–910. issn: 0002–9327, doi: 10.2307/2374789
Acknowledgements
The authors are grateful to Martin Kolář for numerous useful discussions from which some of the ideas used in this article arose. The research was supported by the Max-Planck-Institut für Mathematik Bonn and the ARC Discovery grant DP130103485.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ezhov, V., Schmalz, G. Explicit description of spherical rigid hypersurfaces in
 .
Complex Analysis and its Synergies 1, 2 (2015). https://doi.org/10.1186/2197-120X-1-2
.
Complex Analysis and its Synergies 1, 2 (2015). https://doi.org/10.1186/2197-120X-1-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2197-120X-1-2




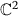 . Indiana Univ. Math. J 2013,62(1):1–32. 10.1512/iumj.2013.62.4833
. Indiana Univ. Math. J 2013,62(1):1–32. 10.1512/iumj.2013.62.4833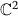 . Trans. Amer. Math. Soc 2010,362(6):2833–2843. issn: 0002–9947, doi: 10.1090/S0002–9947–10–05058–0
. Trans. Amer. Math. Soc 2010,362(6):2833–2843. issn: 0002–9947, doi: 10.1090/S0002–9947–10–05058–0 . Mat. Zametki 1997,62(3):391–403. issn:0025–567X, English translation in Math. Notes, 62(3–4), 329–338 (1998), issn:0001–4346, doi:10.1007/BF02360874 issn:0025-567X, English translation in Math. Notes, 62(3–4), 329–338 (1998)
. Mat. Zametki 1997,62(3):391–403. issn:0025–567X, English translation in Math. Notes, 62(3–4), 329–338 (1998), issn:0001–4346, doi:10.1007/BF02360874 issn:0025-567X, English translation in Math. Notes, 62(3–4), 329–338 (1998)