Abstract
Three-dimensional microscopy has become an increasingly popular materials characterization technique. This has resulted in a standardized processing scheme for most datasets. Such a scheme has motivated the development of a robust software package capable of performing each stage of post-acquisition processing and analysis. This software has been termed Materials Image Processing and Automated Reconstruction (MIPAR™). Developed in MATLAB™, but deployable as a standalone cross-platform executable, MIPAR™ leverages the power of MATLAB’s matrix processing algorithms and offers a comprehensive graphical software solution to the multitude of 3D characterization problems. MIPAR™ consists of five modules, three of which (Image Processor, Batch Processor, and 3D Toolbox) are required for full 3D characterization. Each module is dedicated to different stages of 3D data processing: alignment, pre-processing, segmentation, visualization, and quantification.
With regard to pre-processing, i.e., the raw-intensity-enhancement steps that aid subsequent segmentation, MIPAR’s Image Processor module includes a host of contrast enhancement and noise reduction filters, one of which offers a unique solution to ion-milling-artifact reduction. In the area of segmentation, a methodology has been developed for the optimization of segmentation algorithm parameters, and graphically integrated into the Image Processor. Additionally, a 3D data structure and complementary user interface has been developed which permits the binary segmentation of complex, multi-phase microstructures. This structure has also permitted the integration of 3D EBSD data processing and visualization tools, along with support of additional algorithms for the fusion of multi-modal datasets. Finally, in the important field of quantification, MIPAR™ offers several direct 3D quantification tools across the global, feature-by-feature, and localized classes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Background
The emergence of 3D characterization tools has permitted significant advancement in the field of materials characterization. Various data acquisition techniques exist across length scales [1–6], each with their own strengths and weaknesses. However, data collection is only one in a sequence of steps required for 3D characterization. In fact, the majority of the effort is spent post-collection, with the quality of the reconstructed data critically dependent on these processing steps. The typical processing sequence for 3D characterization is as follows:
Acquisition
The first step in any 3D characterization effort is the collection of three-dimensional data. As stated above, multiple techniques are available. Which one is chosen depends on the questions one wishes to answer and at what length scale they are being asked. For example, if one wishes to accurately quantify the morphology of 1 um precipitates, DualBeam™ FIB/SEM serial sectioning is well suited. In this technique, material is iteratively “sliced” off the edge of a small cantilever using a focused ion beam of Ga+ ions, while subsequent images are acquired with a scanning electron beam [2]. On the other hand, if 100 μm precipitates are of interest, a larger scale technique such as Robo-Met.3D™, where slices are removed via mechanical polishing followed by optical imaging, may be ideal. At the other size-scale extreme, if 10 nm precipitates are the target features, electron tomography would likely be performed in a transmission electron microscope (TEM). A non-destructive technique, X-ray tomography, has garnered much interest in recent years. In this method, multiple X-ray scans are acquired at various sample tilts [3]. This technique can produce a wealth of information, with signal generated from multiple sources.
While each of these techniques is well suited for different length-scales, there is some overlap. For instance, consider the first example of 1 um precipitates. Although DualBeam™ FIB/SEM serial sectioning may be the intuitive choice, if sampling statistics or full precipitate reconstruction are not required, electron tomography offers superior spatial resolution, and in some cases, yields stronger image contrast depending on the image formation signal. Furthermore, despite X-ray tomography’s lower spatial resolution, its non-destructive nature may be a paramount factor, thus rendering it the technique of choice. Regardless of the chosen technique, the steps that follow data acquisition are of equal, if not greater significance to the efficacy of 3D characterization.
Alignment
Image registration, or image alignment, is the process by which similar images are shifted relative to one another in order to maximize agreement of their spatial intensity distribution. As with data collection, multiple techniques are available [7–9]; however, most techniques rely on two steps: image transformation and similarity quantification. That is, the image to register is subjected to an iterative process of image transformation of some class (e.g. rigid, similarity, affine, etc.) followed by similarity measurement (e.g. correlation coefficient, mutual information, etc.) with respect to the reference image. Optimum registration is defined as the image transformation parameters for the given class which yield the maximum similarity value. The pairing of a transformation class with a similarity metric defines the particular technique. The most common technique is known as cross-correlation. Cross-correlation typically performs successive rigid image transformations (translation and/or rotation) while attempting to maximize the normalized correlation coefficient (i.e. dot-product) of the two images. While cross-correlation is quite effective at registering highly random microstructures without the need for fiducial marks, it can be rather inaccurate given a set of similarly spatially oriented features. In these cases, artificial fiducial marks are required. Additional registration techniques involving metrics such as mutual information have been employed [10] and are well suited for the fusion of multi-modal datasets (i.e. those involving multiple collected signals). Selection of the optimum alignment technique strongly influences the success of subsequent processing steps.
Pre-processing
These steps are defined as any which serve to manipulate the raw pixel intensities, typically on the grayscale spectrum, in an effort to improve the accuracy of their eventual segmentation. Such steps include levels adjustments (i.e. brightness/contrast enhancement), noise-reduction filters, and FFT filtering for sectioning artifact removal. Details of the latter will be further discussed in the later pre-processing section.
Segmentation
Segmentation is formally defined as the separation of data into disjoint regions [11]. It is perhaps the most critical step to extracting useful quantitative data from a two- or three-dimensional dataset. In more complex datasets, such as those acquired from titanium alloys, segmentation can involve multiple stages. The most familiar stage is phase segmentation, where pixels are labeled according to the phases which they are deemed to belong. In the case of titanium alloys, a single phase can exist in various morphologies. Therefore, it is often necessary to perform a second stage of segmentation where pixels are assigned to each morphology. Finally, a third stage may involve the discretization of individual microstructural features such as particles or plates. As with data collection and alignment techniques, there exists a multitude of algorithms [12, 13], each suited for overcoming the various challenges of image segmentation. The most common sub-set of segmentation tools are binary, that is, they employ only two classes and assign either a 0 or 1 to each pixel in the dataset. While some view binary segmentation algorithms to be limited in their applicability to multi-class datasets, they offer reduced algorithm complexity and can be readily complemented by a variety of cleanup techniques. The later section on segmentation discusses a data storage framework and user interface which leverages the simplicity of binary segmentation while overcoming many of its multi-class dataset limitations.
Visualization
Visualization was once regarded as the ultimate goal of 3D characterization. As 3D characterization has been applied to a wider problem scope, quantification has become the primary focus of most experiments. However, integrating visualization tools into the processing and quantification framework of any 3D analytical software is paramount to maximizing its characterization potential.
Quantification
The final stage, quantification, is often the purpose of a 3D characterization effort. Its efficacy depends entirely on the metric and corresponding algorithm, as well as the accuracy of the data’s segmentation. The various quantification tools can be divided into three classes: global, feature-by-feature, and localized. Global quantification involves an extraction of a single quantity such as volume fraction, surface area density, or mean linear intercept. In contrast, feature-by-feature quantification extracts a metric such as volume, surface area, or diameter from each feature of interest. This type of quantification is quite common in 3D datasets as many of these individual feature metrics cannot be accurately determined from two-dimensional images. Finally, localized quantification is performed at each point, or vertex, on a reconstructed surface. Such metrics can include local curvature, surface roughness, and thickness. Examples of several localized quantification results are presented in the localized quantification section.
Methods
To be truly robust, any 3D characterization software package must possess a broad array of tools capable of subjecting a dataset to each step described in the previous section. Many powerful software programs have been developed for 3D characterization, both commercial and open source [14–17]. However, few can equip users with extensive toolsets in the areas of alignment, pre-processing, segmentation, visualization, and quantification, with equal attention given to each. A fully integrated toolset, designed by material scientists, would provide an attractive 3D characterization platform. Along that vision, Materials Image Processing and Automated Reconstruction (MIPAR™) has been developed. The software was written and developed in the MATLAB™ environment, with the MATLAB™ compiler enabling MIPAR™ to be executed as a standalone application on Macintosh, Windows, and Linux platforms. MIPAR™ is based upon a modular construction. These modules may be launched from a global launch bar, as well as from within one and another. The modules were designed as standalone programs, each suited for different tasks, and each capable of communication with other modules. MIPAR™ consists of five total modules; three of which are critical for 3D characterization of most materials. The following sub-section will discuss the capabilities and purpose of each of these salient modules, as well as describe MIPAR’s conventional 3D characterization workflow.
Image processor
Nearly all image-processing efforts will originate in the first module known as the Image Processor. This module provides an environment for users to develop a sequence of processing steps known as a recipe. The specific steps and parameters constituting a recipe will vary based on the user’s intent, but the ultimate goal of most recipes is the same: to segment grayscale intensity into a binary image. Much like building an action or macro in Adobe® Photoshop™, a user’s process and parameter selections are recorded real-time, permitting subsequent parameter editing as well as process removal or insertion. Perhaps the Image Processor’s most useful feature is the ability for process and parameter tweaks to propagate down through all subsequent recipe steps. Indeed, parameter optimization is one of most critical aspects of image segmentation, and given the complexity of most recipes, such optimization can be quite time-consuming. The auto-update feature greatly facilitates parameter optimization, increasing the likelihood that users produce near-optimum recipes. Figure 1 reveals the layout of the Image Processor along with lists of many of the included image-processing algorithms, each of which are paired with their own graphical user interface for efficient parameter selection.
Batch processor
Following completion of a recipe, it may be saved and loaded into the second module, the Batch Processor. This module functions to automatically apply the recipe to a series of images, in this case, those collected during a serial sectioning experiment. In addition, tilt-correction, image alignment, and volume reconstructions may all be performed. The Batch Processor was designed to provide a single environment where each of these steps could be performed in one sequence, transforming a set of unaligned raw images into both a stack of aligned slices as well as a segmented, reconstructed volume. The layout of the Batch Processor is shown in Figure 2.
3D Toolbox
This module provides a host of tools for interacting with the image stack and reconstructed volume output from a batch process. The left side of the user interface is dedicated to viewing, manipulating, and exporting the image stack output from the Batch Processor. The image stack is merely a sequence of frames used to examine the slice-to-slice alignment of the raw data. The stack can be viewed with or without the negative space resulting from such alignment. Additionally, the quantitative slice-to-slice translations can be viewed as scatter plots. If severe translations were necessary to align certain slices, resulting in a significantly reduced aligned volume, these slices can be removed and the alignments automatically recalculated. Any desired cropping of the image stack can be performed interactively. Once completed, the modified image stack can be exported as an image sequence for re-processing and segmentation.
The right side of the 3D Toolbox is used for processing, segmenting, cleaning, interacting with, visualizing, and quantifying the voxelized 3D reconstruction. In some cases, a direct 3D segmentation can be superior to conventional slice-by-slice segmentation. In such cases, only the alignment stage would be performed in the Batch Processor, and all pre-processing and segmentation would be performed within the 3D Toolbox directly on the aligned three-dimensional data. If slice-by-slice segmentation was required, the 3D Toolbox can still offer many binary noise reduction, erosion/dilation, and smoothing tools – all performed directly on the 3D segmentation.
On the visualization front, while MIPAR™ does not possess some of the powerful visualization capabilities of commercial applications (e.g. Avizo®), it offers convenient tools for interactively visualizing parts or all of a 3D segmentation as either surface reconstructions or volume renderings. This provides users with direct feedback on their segmentation quality and illustrates relationships between two-dimensional feature cross-sections and the 3D structure to which they belong. Should higher-end visualization be required, the reconstruction may be output in a variety of formats which are compatible with a number of 3D visualization packages, both commercial and open-source. Finally, the 3D Toolbox offers a host of quantification tools in the global, feature-by-feature, and localized categories discussed in the introduction. Example applications of many of these tools are further discussed in the section on quantification tools.
A layout of the 3D Toolbox is shown in Figure 3 along with screenshots of the dropdown menus which offer the pre-processing, segmentation, and quantification tools. Additionally, several interactive tools are labeled which offer functions such as 2D/3D vector and angle measurement, plane indices determination, and single-feature quantification and visualization.
Results and discussion
Pre-processing
As described in the introduction, pre-processing tools are those that manipulate the intensity values of raw data pixels or voxels. Such tools aim to improve image contrast and reduce noise, thus improving the efficacy of subsequent segmentation steps. The following section discusses a unique pre-processing tool included in MIPAR™.
Frequency domain filtering
One issue that can interfere with image segmentation of DualBeam™ FIB/SEM serial section datasets is a milling artifact known as “curtaining”. It receives its name from the surface modulations normal to the incident ion-beam which result from either incomplete or excessive removal of material [18]. These modulations can exist as either surface protrusions or surface relief, both of which are deleterious to image segmentation. In many cases, curtaining can be minimized or eliminated by proper sample preparation, milling parameter selection, and/or advanced techniques. However, for certain sample geometries and microstructures, curtaining is unavoidable, in which case, post-acquisition image filters are the only recourse.
Once such filter is the frequency domain filter (i.e. FFT filter). The fast-Fourier transform (FFT) is a classical algorithm which expresses spatial data as a collection of frequencies. When applied to a two-dimensional image, abrupt intensity transitions are expressed as high frequencies and gradual transitions as low frequencies. The spatial orientation of these transitions determines the vector along which the frequencies are plotted relative to the FFT origin. Once an FFT is computed for a given image, filters may be constructed which either discard or retain certain frequencies. Milling curtains are typically oriented parallel to the milling direction (vertical in most images) and thus exist as a collection of frequencies oriented horizontally within the image As such, curtaining tends to manifest as frequencies which lie along the x-axis of the FFT. By discarding such frequencies and inverting the FFT to recover the filtered image, the intensity of most curtains can be significantly reduced and in some cases removed. Additionally, FFT filtering is effective at reducing the influence of similarly oriented scratches in 2D and 3D datasets as they manifest similar to milling curtains as frequency bands in an FFT.
MIPAR’s Image Processor offers a graphical environment for the construction and application of FFT filters including low-pass, high-pass, annular, and custom filters. In the case of curtain reduction, a custom filter can be created as a thick line which discards all frequencies which lie along the x-axis. It should be noted that frequencies in close proximity to the origin should be retained as these low frequencies contribute to a majority of the image contrast. As examples, slices from two DualBeam™ FIB/SEM serial sections: a hydrogen blister in a tungsten alloy and a bimodal microstructure in [α + β]-processed Ti-6Al-4 V (wt%) (Ti-64) were subjected to FFT filtering for curtain reduction. This particular custom filter was a horizontal masking line with a thickness of 6 pixels (i.e. 110 cycles/micron in frequency units). When applied to each slice, the segmentation of both datasets vastly improved. Figure 4 displays MIPAR’s graphical interface for FFT filtering along with the slices and corresponding FFTs before and after filtering.
Screen capture of the FFT filtering user interface along with example applications. (a) Layout of the FFT filtering graphical user interface (GUI) as well as cross-sectional slices and corresponding FFTs from a hydrogen blister in a tungsten alloy (b) before and (c) after FFT filtering. Slices though [α + β]-processed Ti-64 are shown with their FFTs (d) before and (e) FFT filtering.
Segmentation
Optimization via mutual information
Perhaps the most critical, yet often unexplored areas of 2D and 3D segmentation are those of objective parameter selection and segmentation accuracy quantification. In fact, nearly all aspects of most segmentation algorithms have become fully automated with the exception of parameter selection. The influence of these parameters on subsequent quantification can be profound. In some cases, metrics such as volume fraction acquired from a 2D image can vary by several volume percent from an under- or over-segmentation of a single pixel. In a 3D dataset, segmentation fluctuations can result in even more dramatic volume fraction variations. Dataset to dataset, these fluctuations can result from variations in image quality and contrast, as well as user bias.
Prior to exploring a method for objective segmentation parameter selection, one must first define the concept of segmentation accuracy. Consider a volume of material containing precipitates of a certain shape and size. An image acquired of such precipitates is a product of sample preparation and image formation physics. Any method that attempts to quantify the “accuracy” of the image’s segmentation, would be doing so relative only to the image, and is therefore entirely dependent on how faithfully that image represents the actual microstructure. Therefore, when discussing the notion of segmentation accuracy, one must consider the segmentation-to-image comparison separate from that of image-to-microstructure. The image-to-microstructure comparison has historically been left to the judgment of the experimenter. Recent advances in the field of forward modeling; however, have the potential to greatly contribute to this area [19, 20].
The segmentation-to-image comparison is one in which information theory tools can contribute. One such tool is mutual information. By definition, mutual information describes the similarity between two variables, in this case, two images [21]. Eq. 1 displays a mathematical expression for mutual information:
In this expression, H(X) represents the entropy, or uncertainty, of the original image X. H(X|Y) represents the conditional entropy of the original image X when the segmented image Y is known. Their subtraction therefore describes the reduction in uncertainty of original image X upon knowing its segmentation Y, or in other words, how well the segmentation describes the original image. Normalizing by the entropy of the original image yields a range of 0 to 1 as possible values of mutual information. A mutual information of 0 implies that the segmentation in no way describes the original image, while a mutual information of 1 implies that the image is perfectly described the segmentation.
Using mutual information as the quantifying metric, a mechanism has been developed and incorporated into MIPAR™ which allows users to objectively determine the optimum parameters for a given image-processing algorithm. Algorithms such as global thresholding, adaptive thresholding, erosion and dilation, feature rejection, and watersheding are all candidates for optimization. When either of these processes is selected within a recipe, an “Optimize” button becomes active at the top of the recipe panel. Selecting this button spawns a series of windows allowing users to select the parameter ranges from which to identify the optimum parameter set. Using either a sub-area or the entire image, the grayscale data is segmented over all possible parameter sets within the specified range. The mutual information between each segmentation and the original image is computed, and the parameter set which yields the maximum mutual information is chosen as optimum. This tool is currently applicable to two-dimensional processing algorithms with a maximum of two parameters; however, extension of this tool to three-dimensional volumes and multi-dimensional parameter space is an ongoing effort.
As an example, the adaptive thresholding of an SEM micrograph of secondary Ni3Al γʹ precipitates is optimized. Briefly, adaptive thresholding assesses each pixel relative to a statistic (typically the mean) of its local neighborhood. This algorithm involves two parameters: the window size which defines a pixel’s neighborhood, and the threshold by which a pixel’s intensity value must exceed its local mean in order to be selected. The threshold may also be expressed as the percentage of the local mean that a pixel’s intensity must meet or exceed. In this example, the window size was fixed at 15 pixels, and the threshold value was allowed to vary from 50% to 110% in steps of 1%. Figure 5 displays the result of the optimization along with several candidate segmentations determined during the process.
A plot of normalized mutual information (see Eq. 1 ) vs. threshold value for the adaptive thresholding of secondary Ni3Al γ’ precipitates in a nickel-base superalloy. Five candidate optimum segmentations are shown beneath the plot. For this experiment, a threshold value of 90 yielded maximum mutual information between the adaptive threshold and original image.
Although this technique does not address the fidelity between image and microstructure, it does provide a method for consistently and objectively determining processing parameters across images and users. Additionally, if a recipe step has been optimized in MIPAR’s Image Processor, the optimization process is repeated for every image to which that recipe is applied in the Batch Processor. In this way, slice-to-slice contrast variations within a 3D dataset may be overcome by allowing parameters of several recipe steps to dynamically adjust to a given image’s intensity profile. Other research has been performed on the topic of optimizing segmentation via mutual information [22, 23]. However, to the best of the author’s knowledge, MIPAR™ exhibits the first incorporation of this method into a graphical software interface. This will permit its application to a variety of problems and microstructures so that the extent of its strengths and limitations can be thoroughly explored.
Feature-sets
Up to this point, this paper has discussed segmentation exclusively in a binary sense, where each pixel or voxel in a grayscale dataset is labeled as either a 0 or 1. Historically, this has worked well for the segmentation of two-phase microstructures, or for the isolation of a certain phase or feature type. As a result, the image processing community has developed an extensive library of binary segmentation and cleanup routines [24], all of which are computationally efficient. However, in many image-processing frameworks, binary segmentation can limit the type of microstructures that can be processed since any with more than two phases of interest are incompatible with binary classification. For two-dimensional images, this is not a great inconvenience since a separate binary segmentation can be performed for each phase interest with minimal overhead. However, the size and storage demands of 3D datasets make this approach less practical. Furthermore, by discretizing each phase or feature type into an independent segmentation and file, any metrics that quantify one phase or feature type with respect to another are quite difficult.
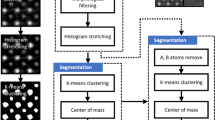
Rather than develop MIPAR™ as a framework to handle multi-class 3D segmentations, a data structure was developed wherein separate binary segmentations of the same dataset could be stored as layers in a multi-dimensional space. Furthermore, this structure can effectively store multi-modal datasets where raw data is collected from several techniques (e.g. secondary/backscatter electron imaging, EBSD, EDS, etc.). A schematic of this multi-dimensional structure is shown in Figure 6. Under this format, every voxel receives a set of multi-dimensional coordinates which identify the voxel’s placement in 3D Cartesian space as well its position in other dimensions such as data type and data level. A voxel’s location in the “ith” dimension (see Figure 6) defines the binary segmentation to which it belongs. The different segmentations are termed feature-sets.
The initial segmentation of the original data produces the first feature-set, whether performed slice-by-slice in the Batch Processor, or three-dimensionally in the 3D Toolbox. A dropdown menu allows users to add additional feature-sets, as well as switch to, remove, rename, or merge existing feature-sets. By treating multi-class segmentations as a set of concatenated binary segmentations, interacted with using a simple interface, the simplicity and computational efficiency of binary data is preserved, while the complexity of multi-phase datasets and inter-phase quantification can be handled.
An example application of the feature-set framework is presented in Figure 7. This particular dataset from a nickel-base superalloy consisted of FCC γ grains, carbides, and twins [25]. Thus, three binary segmentations were necessary to fully characterize a single grain within the microstructure. Under the feature-set framework, three fairly complex segmentation recipes were carried out independently, yet their results combined into a single data structure. A fourth feature-set was then generated from the merging of the first three, where each voxel was labeled according to the feature-set from which it originated. This fourth feature-set was employed to visualize the multi-phase microstructure in three dimensions.
Screen capture of the feature-set management user interface along with example applications. (a) A screen-capture of the upper-right portion of the 3D Toolbox (see Figure 9) which contains the user-interface for interacting with and adding feature-sets. Also shown are (b) example slices from each of the three feature-sets constructed for a three-phase nickel-base superalloy along with (c) a visualization of the reconstructed 3D microstructure.
3D EBSD and data fusion
The emergence of high-speed electron backscatter diffraction (EBSD) cameras has increased the popularity of three-dimensional EBSD. These datasets permit a deeper investigation of 3D microstructures and have advanced the understanding of microstructural evolution. While robust commercial software has long existed for the analysis of two-dimensional EBSD scans, analogous 3D software has been somewhat underdeveloped. Recently developed software programs (e.g. DREAM.3D™ [16]) offer unique collections of 3D EBSD data processing tools housed in graphical interfaces. These programs also provide tools for both 3D EBSD quantification and synthetic microstructure generation. However, few software titles offer tools for the fusion of 3D multi-modal datasets (i.e. datasets whose voxels are comprised of multiple discrete variables and/or spectra).
MIPAR’s multi-dimensional data structure offers a promising solution to multi-modal data storage and processing. For example, tools for 3D EBSD data import, cleanup, and visualization (see Figure 8(a)) have been developed. Figure 8(b, c) presents two 3D EBSD reconstructions that were imported as raw data into MIPAR™, cleaned, and visualized using inverse pole figure colormaps. These tools will be extended to handle the input of compositional measurements from techniques such as EDS and WDS. Upon adding these tools to MIPAR’s comprehensive 3D characterization package, and by storing crystallographic data along side BSE/SE/optical intensity, data fusion tools remained as the final requisite for handling multi-modal data.
Screen captures of the 3D EBSD data processing tools along with example applications. (a) Screen-captures of 3D EBSD import, cleanup, and quantification tools along with (b) a 3D EBSD reconstruction of a twin and parent grain in FCC nickel as well as (c) a 3D EBSD reconstruction of intersecting α-laths in Ti-6Al-2Sn-4Zr-6Mo (wt%) (Ti-6246).
The primary challenge related to data fusion involves the registration of voxels of different dimensions. Separate datasets must first be resampled such that their voxel dimensions match. Second, the data must be registered. Inter-modal registration presents greater challenges than conventional serial section alignment and often requires non-rigid volume transformations. MIPAR™ has already incorporated the open-source Medical Image Registration Toolbox (MIRT) [26] for the free-form registration of 2D images. At present, MIPAR™ offers both manual and automated tools for assigning crystallographic orientations and phase identifications to BSE/SE/optical datasets.
Quantification
As stated earlier, quantification has become the desired result of most 3D characterization experiments. Therefore, MIPAR™ was equipped with a host of tools in the areas of global, feature-by-feature, and localized quantification. The following sub-sections will present several examples of the included tools.
Global quantification
The most basic 3D quantification metrics are classified as global. These are defined as any which extract a single value from a reconstructed volume. In the case of binary segmentations, they tend to operate on those voxels which have been assigned to the features or phase of interest. Common global metrics include total volume, volume fraction, total surface area, surface area density, surface area per volume, and mean linear intercept. Each of these and several others are available in MIPAR’s 3D Toolbox from a dropdown menu (see Figure 3).
Feature-by-feature quantification
Since 3D reconstructions tend to capture multiple microstructural features in their entirety, individual measurements of each discrete feature are often desired. Such metrics are of the class termed “feature-by-feature”. Feature labeling is performed automatically within MIPAR™ using a conventional 6-voxel-connectivity scheme. Discretization can be aided using a variety of algorithms including watersheding and iterative erosion/dilation techniques. Once the segmented features are sufficiently discretized, a graphical interface allows users to extract specific metrics from each labeled feature. Figure 9 displays this interface and reveals the list of available metrics.
Localized quantification
Additionally, 3D quantification can be performed locally about each point on the surface of a reconstructed feature. These points are known as vertices, and are the Cartesian coordinates in the sample reference frame of all points which constitute a reconstructed surface. Incorporating codes from the MATLAB™ file exchange, MIPAR™ can report fundamental parameters from each vertex such as Cartesian position, local normal, and local curvature. More complex algorithms have also been developed including thickness and roughness mapping. The former measures the local thickness at each vertex by measuring the distances between opposing vertices which lie along a vector parallel to either the local surface normal or a user-defined global normal. Roughness mapping is accomplished by fitting a plane or curved surface to the quantified vertex positions and subsequently coloring the surface according to each vertices’ elevation relative to the fit plane or surface.
Regardless of the quantities measured at each vertex, all of which are exported as comma-separated text files, the reconstructed surface can subsequently be colored according to each vertices’ measurement. A simple dropdown menu allows users to select this visualization scheme and choose the data on which to base the localized coloring. Therefore, additional custom algorithms can be subsequently performed on MIPAR’s exported vertex measurements in software such as Microsoft Excel®, the results of which can be color-mapped on the associated surface. Figure 10 reveals example applications of visualized local quantification such as local curvature, topography, and thickness.
Example applications of localized quantification visualization. Visualizations of localized quantification such as (a) local curvature of equiaxed-α particles in [α + β]-processed Ti-64, (b) local thickness of an α-lath in Ti-6Al-2Sn-2Zr-2Mo-2Cr (wt%) (Ti-62222), and (c) local topography (i.e. roughness) of an FCC γ/FCC γ grain boundary in a nickel-base superalloy.
Advantages of MATLAB™ Development
Although some have questioned the utility of MATLAB™ as a professional software development platform, it offers several advantages over other computing languages in the area of 2D and 3D data processing. For one, MATLAB™ is appropriately an acronym for Mat rix Lab oratory, and is thus equipped with several toolboxes and functions specifically designed for two- and three-dimensional matrices – precisely the raw format of 2D images and 3D volumes. These built-in libraries offer rapid development and powerful functionality to any 2D or 3D analytical software developed within MATLAB™. In MIPAR’s case, they comprise roughly 55% of the constitutive functions.
Second, included in this built-in functionality are a number of 2D and 3D visualization tools. As discussed in the introduction, even the most robust analytical software cannot reach its full potential if it fails to provide users immediate visual feedback on the result of a 2D or 3D filter. MATLAB’s built-in visualization library has aided in MIPAR’s evolution as both a processing and visualization platform.
Third, MATLAB’s broad user-base has resulted in extensive public code repositories, the most popular of which is the MATLAB™ File Exchange. The numerous codes contained within such repositories are provided open source, under the stipulation that the code’s license file be included with the deployed application. In MIPAR’s case, several algorithms were harvested from these repositories and make up nearly 20% of its function count. The corresponding authors have been listed as contributors to the software and their licenses included. This contribution has accelerated MIPAR’s growth and underlined the fact that a single developer cannot produce the most efficient form of every algorithm, nor is it effective to “reinvent the wheel” when it comes to well-accepted data processing algorithms.
Finally, MATLAB’s popularity has led to the development of third-party commercial software written specifically for MATLAB™ (e.g. Jacket™ by Accelereyes®). This particular software offers a collection of MATLAB™ codes written to run on the graphics processor unit (GPU). Such codes are often orders of magnitudes faster than corresponding CPU-based codes. Functions such as GPU-based parallel for-loops have dramatically accelerated complex image-processing algorithms offered in MIPAR™.
Conclusions
The paradigm of 3D data processing has motivated the development of a multi-faceted 3D processing/analytical software package named MIPAR™ (Materials Image Processing and Automated Reconstruction). Through development in MATLAB™, MIPAR™ takes advantage of MATLAB’s powerful 2D and 3D data processing libraries, public code repository, and third-party GPU-acceleration software, while being deployed as a standalone cross-platform application.
In addition to offering many conventional pre-processing filters, MIPAR™ includes a unique graphical interface for the development and application of noise-reducing FFT filters which are effective at reducing the influence of data acquisition artifacts such as ion-milling curtains and polishing scratches. Furthermore, in the area of segmentation, MIPAR™ offers an interactive framework for the automated optimization of segmentation parameters through the use of mutual information. Once optimized, MIPAR’s numerous binary segmentation and cleanup algorithms can be employed for the effective segmentation of even complex, multi-phase 3D microstructures. Such is possible via a multi-dimensional data structure which works in conjunction with a simple user interface to permit the multi-dimensional layering of multiple binary segmentations of the same 3D dataset. Although MIPAR™ offers nowhere near as comprehensive a 3D EBSD toolset as other programs, its employed 3D data structure has enabled the import, basic processing, quantification and visualization of 3D EBSD data, as well as import/export functionality to and from additional programs. Future integration of such programs with MIPAR™ would offer a powerful 3D EBSD characterization platform. Additionally, MIPAR’s multi-dimensional data structure has permitted the development of tools for the fusion of multi-modal datasets. In the near feature, the medical image registration toolbox (MIRT) 3D free-form registration tools will be incorporated into MIPAR’s 3D Toolbox for the automated registration of 3D EBSD with BSE/SE/optical datasets.
In the area of quantification, MIPAR™ includes common global quantification algorithms for metrics such as volume fraction, surface area density, and mean linear intercept. In addition, a variety of direct 3D feature-by-feature metrics such as individual volume, surface area, shape factor, and aspect ratio may be extracted. Finally, MIPAR™ offers a simple yet powerful means of locally quantifying a variety of metrics at each point on a reconstructed surface and subsequently visualizing the spatial distribution of such measurements on various color scales. The available metrics range from basic, such as position, local normal, and local curvature, to complex, such as local thickness and surface roughness.
References
Spowart JE: Automated Serial Sectioning for 3D analysis of Microstructures. Script Materialia 2006, 55(1):5–10. 10.1016/j.scriptamat.2006.01.019
Uchic MD, Holzer L, Inkson BJ, Principe EL, Munroe P: Three-Dimensional Beam Tomography. 2007, 32(May):408–416.
Elliott JC, Dover SD: X-ray microtomography. J of Microscopy 1982, 126(2):211–213. 10.1111/j.1365-2818.1982.tb00376.x
Dierksen K, Typke D, Hegerl R, Koster AJ, Baumeister W: Towards automatic electron tomography. Ultramicroscopy 1992, 40(1):71–87. 10.1016/0304-3991(92)90235-C
Bronnikov AV: Phase-contrast {CT}: {Fundamental} theorem and fast image reconstruction algorithms. Developments in X-Ray Tomography V 2006, 6318: Q3180.
Cloetens P, Ludwig W, Baruchel J, Dyck D, Van Landuyt J, Van Guigay JP, Schlenker M: Holotomography: {Quantitative} phase tomography with micrometer resolution using hard synchrotron radiation {X}-rays. Appl Phys Lett 1999, 75(19):2912–1914. 10.1063/1.125225
Brown LG: A survey of image registration techniques. ACM Comput Surveys (CSUR) 1992, 24(4):325–376. 10.1145/146370.146374
Roshni V, Revathy K: Using mutual information and cross correlation as metrics for registration of images. J of Theoretical & Applied Information 2008, 4: 474–481.
Maes F, Collignon A, Vandermeulen D, Marchal G, Suetens P: Multimodality image registration by maximization of mutual information. Medical Imaging, IEEE Transactions on 1997, 16(2):187–198. 10.1109/42.563664
Gulsoy E, Simmons J, De Graef M: Application of joint histogram and mutual information to registration and data fusion problems in serial sectioning microstructure studies. Scripta Materialia 2009, 60(6):381–384. 10.1016/j.scriptamat.2008.11.004
Russ JC: Practical Stereology. In Practical Stereology. The Netherlands: Kluwer Academic Pub; (1986:1–381.
Pal NR, Pal SK: A review on image segmentation techniques. Pattern Recognition 1993, 26(9):1277–1294. 10.1016/0031-3203(93)90135-J
Haralick RM, Shapiro LG: Image segmentation techniques. Computer Vision, Graphics, and Image Processing 1985, 29(1):100–132. 10.1016/S0734-189X(85)90153-7
Westenberger P, Estrade P, Lichau D: Fiber Orientation Visualization with Avizo Fire®. Wels, Austria: Conference of Industrial Computed Tomography (ICT) 2012; 2012.
Rasband WS: ImageJ, U.S. National Institutes of Health. Bethesda, Maryland, USA: U.S. National Institutes of Health; , 1997—2012 http://imagej.nih.gov/ij/a
Groeber M, Jackson M: DREAM.3D: Digital Representation Environment for Analyzing Microstructure in 3D. BlueQuartz Software. BlueQuartz Software; 2011–2013.
Henderson A: ParaView Guide. A Parallel Visualization Application: Kitware Inc.; 2007.
Volkert CA, Minor AM: Focused Ion beam microscopy and micromachining. MRS Bulletin 2007, 32(05):389–399. 10.1557/mrs2007.62
Venkatakrishnan SV, Drummy LF, Jackson MD, Graef M, Simmons J, Bouman C: A model based iterative reconstruction algorithm for high angle annular dark field-scanning transmission electron microscope (HAADF-STEM) tomography. IEEE transactions on image processing : a publication of the IEEE Signal Processing Society 2013, 22(11):4532–44.
Suter RM, Hennessy D, Xiao C, Lienert U: Forward modeling method for microstructure reconstruction using x-ray diffraction microscopy: Single-crystal verification. Review of Scientific Instruments 2006, 77(12):123905. 10.1063/1.2400017
MacKay DJC: Information theory, inference and learning algorithms. Cambridge, United Kingdom: Cambridge university press; 2003.
Rigau J, Feixas M, Sbert M, Bardera A, Boada I: Medical image segmentation based on mutual information maximization. Medical Image Computing and Computer-Assisted Intervention - Miccai 2004, Pt 1, Proceedings 3216 edition. 2004, 135–142.
Gonzalez RC, Woods RE: Digital Image Processing. Upper Saddle River, New Jersey: Pearson/Prentice Hall; 2008.
Shi DJ, Liu ZQ, He J: Genetic algorithm combined with mutual information for image segmentation. Advanced Materials Res 2010, 108–111: 1193–1198.
Carter JLW, Zhou N, Sosa JM, Shade PA, Pilchak AL, Kuper MW, Mills MJ: Characterization of strain accumulation at grain boundaries of nickel-based superalloys. Edited by: Huron ES, Reed RC, Hardy MC, Mills MJ, Montero RE, Portella PD, Telesman . Seven Springs, Pennsylvania: Superalloys; 2012:43–52.
Myronenko A: Medical Image Registration Toolbox [Computer software]. Portland, OR: Oregon Health & Science University; 2007.
Acknowledgements
The authors gratefully acknowledge Nicholas Hutchinson, Dr. Santhosh Koduri, Dr. Paul Shade, Dr. Jennifer Carter, and Samuel Kuhr for their contributions in the area of data acquisition, as well as all additional supporters whose data collection efforts and software-related feedback have greatly contributed to this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
JMS carried out the software development, dataset post-processing, and drafted the manuscript. DEH carried out data acquisition and provided suggestions for software development. BW carried out data acquisition and provided suggestions for software development. HLF provided oversight to the work, managed the affiliated authors, and reviewed the manuscript. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sosa, J.M., Huber, D.E., Welk, B. et al. Development and application of MIPAR™: a novel software package for two- and three-dimensional microstructural characterization. Integr Mater Manuf Innov 3, 123–140 (2014). https://doi.org/10.1186/2193-9772-3-10
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1186/2193-9772-3-10