Abstract
In the clinical practice, many diseases such as glioblastoma, leukemia, diabetes, and prostates have multiple subtypes. Classifying subtypes accurately using genomic data will provide individualized treatments to target-specific disease subtypes. However, it is often difficult to obtain satisfactory classification accuracy using only one type of data, because the subtypes of a disease can exhibit similar patterns in one data type. Fortunately, multiple types of genomic data are often available due to the rapid development of genomic techniques. This raises the question on whether the classification performance can significantly be improved by combining multiple types of genomic data. In this article, we classified four subtypes of glioblastoma multiforme (GBM) with multiple types of genome-wide data (e.g., mRNA and miRNA expression) from The Cancer Genome Atlas (TCGA) project. We proposed a multi-class compressed sensing-based detector (MCSD) for this study. The MCSD was trained with data from TCGA and then applied to subtype GBM patients using an independent testing data. We performed the classification on the same patient subjects with three data types, i.e., miRNA expression data, mRNA (or gene expression) data, and their combinations. The classification accuracy is 69.1% with the miRNA expression data, 52.7% with mRNA expression data, and 90.9% with the combination of both mRNA and miRNA expression data. In addition, some biomarkers identified by the integrated approaches have been confirmed with results from the published literatures. These results indicate that the combined analysis can significantly improve the accuracy of classifying GBM subtypes and identify potential biomarkers for disease diagnosis.
Similar content being viewed by others
Introduction
Many diseases including cancers have multiple subtypes. For example, leukemia has four main categories: acute lymphoblastic leukemia (ALL), acute myelogenous leukemia, chronic lymphocytic leukemia, and chronic myelogenous leukemia. Each of these categories can be further divided into different subtypes [1]; for example, ALL can be further subtyped into six types [2]. Glioma has four subtypes, including oligodendroglioma, anaplastic oligodendroglioma, anaplastic astrocytoma, and glioblastoma multiforme (GBM) [3]. Prostate cancer has three major subtypes [4]. An accurate and effective classification of those subtypes based on genomic data will result in personalized treatments of the cancer in terms of a particular subtype. In this article, we are interested in the subtyping of GBM, which is a kind of glioma and is the most common form of malignant brain cancer in adults [5]. There is an increasing interest in classifying multiple subtypes of GBM based on its genomic measurements. Most of the existing works are based on gene expression data only. Benjamin et al. [6] classified two types of GBM in adults and found that the genes EGFR and TP53 were important in discriminating the two subtypes. Nutt et al. [7] built a k-nearest neighbor model with 20 features to classify 28 glioblastomas and 22 anaplastic oligodendrogliomas and found that the class distinctions were significantly associated with survival outcome (p = 0.05). Noushmehr et al. [8] separated a subset of samples in GBM from The Cancer Genome Atlas (TCGA) project, which displayed concerted hypermethylation at a large number of loci. The datasets we used to subtype GBM are also from TCGA. The subtypes of GBM samples in TCGA includes: pro-neural, neural, classical, and mesenchymal [9]. The GBM data we have tested include both miRNA expression and mRNA expression data. The miRNAs, also called microRNAs, are short non-coding RNA molecules that were recently found in all eukaryotic cells except fungi, algae, and marine plants. The human genome may contain over 1,000 miRNAs [10]. Aberrant expressions of miRNAs have been found to be related to many diseases, including cancers [11, 12]. They play an essential role in tissue differentiation during normal development and tumorigenesis [13].
In the last decade, the development of genomic techniques enables the availability of multiple data types on the same patient, such as mRNA or gene expression, SNP, miRNA expression, and copy number variation data. It is well recognized that a more comprehensive analysis result could be obtained based on integrating multiple types of genomic data than using an individual dataset. Soneson et al. [14] investigated the correlation between gene expression and copy number alterations using canonical correlation analysis for leukemia data. A web-based platform, called Magellan, was developed for the integrated analysis of DNA copy number and expression data in ovarian cancer [15], which found significant correlation between gene expression and patient survival. Troyanskaya et al. [16] developed a Bayesian framework to combine heterogeneous data sources to predict gene function with improved accuracy. A kernel-based statistical learning algorithm was also proposed in the combined analysis of multiple genome-wide datasets [17]. In this article, we propose a novel classifier based on the compressed sensing (CS) theory that we have been working with.
The CS technique enables compact storage and rapid transmission of large amounts of information. The technique can be used to extract significant statistical information from high-dimensional datasets [18]. The CS technology has been proven to be a powerful tool in the signal processing and statistics fields. It demonstrates that a compressible signal can be recovered from far fewer samples than that needed by the Nyquist sampling theorem [19]. Our recent work used a CS-based detector (CSD) for subtyping leukemia with gene expression data [20]. The CSD achieved high classification accuracies, with 97.4% evaluated with cross-validation and 94.3% evaluated with an independent dataset. The CSD showed better performance in subtyping two types of leukemia compared to some traditional classifiers such as the support vector machine (SVM), indicating the advantage of the CSD in analyzing high-dimensional genomic data. In this article, we extended the CSD to multiple data types and proposed a detector called MCSD. In particular, we applied the MCSD to the subtyping of four types of GBM by combining miRNA expression and mRNA expression data. We present a novel combined analysis method based on the CS and demonstrate that the classification performance can significantly be improved in subtyping four types of GBM, with both miRNA expression and mRNA expression data.
Methods and materials
Data collection
The GBM data used in this study are publicly available from the website of TCGA [21]. The patients in the dataset can be classified into four subtypes, i.e., pro-neural, neural, classical, and mesenchymal [9]. The genomic data include miRNA expression (1,510 probes) and mRNA expression data (22,277 probes). We randomly divided the data (including 115 patients with both miRNA and mRNA expression data) into two sets: training and testing datasets. The total number of patients in the training dataset was 60 with 15 patients in each group. The testing dataset had 55 patients, with 17 pro-neural, 3 neural, 17 classical, and 18 mesenchymal subtypes (as listed in Table 1). The same number of patients in each subtype for training data was used for reducing the bias in the model building. Meanwhile, the numbers of patients in training and testing were approximately the same.
For multiple types of genomic data (e.g., miRNA expression data, mRNA expression data, etc.), we used x1i to denote the data vector for the i th sample in data 1 (e.g., miRNA expression), x2i to denote the data vector for the i th sample in data 2 (e.g., mRNA expression), and x ni to denote the data vector for the i th sample in data n. The combined data for the i th sample is , which is arranged in a cascaded manner.
MCSD
Bayesian classifier
To classify a given observation y to one of n classes, we define the actual class (“ground truth”) to which it belongs as g; the class to which it is assigned (“decision”) as d. The n classes are defined as: π1,π2,…,π n . Let U πi (y ,g) be the utility of assigning y, actually from π g , to π i . The “utility” is negative relevant to the Bayes Risk (BR) [22], which is the minimum classification error. Thus, we make: U = 1-BR. The two-class one-dimensional BR (shaded area in Figure 1) can be calculated by
where y0 is the decision boundary, P1P2 are the prior probabilities and P1(y),P2(y) are the conditional probability density functions of the two classes, respectively (shown in Figure 1).
Let us extend the BR to n classes and N dimensions. Then Equation (1) can be rewritten as
where P j is the prior probability of a given subject belonging to the class π j , j = 1,…,n; P j (y) is the conditional probability density function of the class π j , and Ω i is the Bayesian decision region for class π i [23].
For multi-class classification, an ideal detector should yield
where
where P(d = π i |g = π j ) denotes the probability of assigning a given observation y, actually belonging to π j , to π i. δ ij is the Kronecker’s delta.
According to the ideal observer decision theory [22], a decision is selected only if its expected utility is greater than the expected utility of any others. Thus, for any given observation y, we decide d = π i iff
From Equation (2) and the relationship of utility and BR, we know “utility” is a number that can be calculated. We denote that number as Ui|j to express the utility of assigning a given observation y, actually belonging to π j , to π i . The inequality (4) can be written as
We apply Bayes’ rule
where P y (y|g = π k ), k = 1,…,n, is the probability density function for the signal observations. According to Inequality (5), we decide d = π i iff
That is known as maximum likelihood estimation. Specifically, the class label of the testing sample y is given by
If we assume π1, π2,…,π n have the same prior probability, i.e., . The detector (8) can be rewritten as
The calculation of the utility is shown in the Additional file 1.
Dimension reduction using CS
To reduce the dimension of original sample, we design a projection (sparse) matrix Φ , called compress matrix. The generation of the compress matrix can be formulated as a sparse representation problem as in Equation (10)
where is the projected sample, M is the dimension of the sample after the projection, y i is the i th column in the compressed signal, c is the total number of columns in the compressed signal, is the original signal, and N is the dimension of the original signal and N >> M. The matrix is a sparse matrix, with most of the entries ‘0’s. The compress matrix Φ projects the original sample S to a much smaller dimensional signal Y. The original sample may contain redundancy; through this projection, the original sample can significantly be compressed and compactly represented, which usually lead to better classification performance. Suppose we have n groups, with c1 training samples in group 1, c2 training samples in group 2, and so forth, c n training samples in group n, and c = c1 + c2 + ··· + c n for and . The transpose of Equation (10) is
Let denote the j th column of ΦT, and denote the j th column of YT, where j = 1, 2,…,M. Then Equation (11) can be rewritten as
The linear system given by (12) is an underdetermined system, which can be solved by using l-1 norm minimization algorithm such as Homotopy method, or the least angle regression method [24]. The l-1 norm optimization problem reads
subject to
where ‖(ΦT) j ‖1 is the l-1 norm of the vector (ΦT) j , i.e., the sum of the absolute values of entries in vector (ΦT) j . Obviously, the compress matrix Φ projects the original signal to a much smaller dimensional signal . Instead of dealing with the original signal, we only use and in the subtyping procedure, leading to a fast classification.
Determination of feature vector
We need to select significant features to represent the original data before we classify the data. For each sample, we extracted five feature characteristics [20]: the mean and the standard deviation of each group’s standard deviation (MeanStd, StdStd), the standard deviation of the means of all the groups (StdMean), and the mean and standard deviation of Pearson’s linear correlation coefficient (MeanCorr, StdCorr) between the samples and their class label vector. Therefore, for the i th sample, we have a five-dimensional feature vector as follows:
where i = 1,2,…,N, and N is the number of samples. Each element in the vector V i has been normalized by its overall maximum value so that its value is between 0 and 1, i.e., V i ∈ [0, 1]. A number of M informative features were selected by setting the threshold values of V i . If a feature is informative or significant, we expect that the values from different patients within the same subtype are similar while the differences among different subtypes are relatively large. In addition, it is easy to understand that, if the correlation between the feature vector and the class label is high, the feature vector can serve as a significant biomarker to distinguish the subtypes. According to the above analysis, matrix Y in Equation (10) is built by those features with low MeanStd, StdStd, StdCorr while high StdMean, MeanCorr, which are significant for the classification.
Classifier based on CS
In this particular study of subtyping four types of GBM with miRNA expression and mRNA expression data, we make a hypothesis that the data follow a normal distribution. In other words, the probability density function for the data is
where is a given observation; is the mean of a sample; and σ is the standard deviation of the data.
After compressing the original sample, the probability density function (Equation 14) is still Gaussian but with different mean and standard deviation given by [18]
where is a compressed observation; is a known signal and Φ is the compress matrix. The MCSD used in this study is constructed by substituting Equation (15) into Equation (9) for maximum likelihood estimation.
The classification algorithm is described as below.
-
1.
Inputs: training dataset and testing dataset
-
2.
Normalize the rows of the training and the testing datasets to the range of [0,1]
-
3.
Select informative features according to the feature selection criteria
-
4.
Calculate compress matrix by the training dataset by Equation (14)
-
5.
Identify the class of the compressed testing data by Equation (9), where the probability density function is given by Equation (15).
There are many other classifiers such as SVM that can be used. But our purpose here is to show that dimension reduction with the CS can improve subsequent classification and the often used Bayesian classifier is chosen.
Results
We subtyped four types of GBM with multiple genomic data types (e.g., miRNA expression, mRNA expression, and their combinations) from TCGA. The MCSD was first trained by the training data with known class labels, and was then employed to detect subtypes in another independent testing dataset. The classification accuracy by the MCSD was compared with that without using MCSD. The classification performance between using the combined data types and using a single type of data was also compared.
Table 2 shows the comparison of the GBM classification accuracy for the testing dataset, with and without the compress matrix used in our algorithm (see Section “Methods and materials”). The results were obtained on three types of data, i.e., miRNA expression data, mRNA expression data, and their combinations. The classification accuracy is defined as the ratio between the number of correctly labeled samples and the number of total samples. The result calculated by the non-compressed detector had a classification accuracy of 41.8% with miRNA expression data. However, when we used the MCSD to classify the four subtypes, the accuracy of classifying the testing dataset was 69.1%, with 54 selected informative features out of 1,510 features. When we tested the classifiers on the mRNA expression data, the result calculated by the non-compressed detector was 32.7%. However, the classification result with the MCSD was 52.7%, which employed a subset of the features, 432 out of 22,277 features.
We also tested if the classification performance of the MCSD was better than non-compressed detector in the combined analysis of both miRNA expression and mRNA expression data as shown in Table 2. The subtyping accuracy by the non-compressed detector was 32.7%. The classification accuracy by the MCSD showed a significant improvement over the non-compressed detector. The accuracy was 90.9% (121 informative features selected or 145 informative features selected). The 121 features selected are shown in Additional file 2 with the probes and the corresponding symbols.
Figure 2 demonstrates the classification accuracy when different numbers of informative features were employed. The combined analysis of the two types of genome-wide data was always able to achieve a significant higher subtyping accuracy than any single data type analysis when the same number of informative features were used (with a subset of features less than 450), indicating the advantages of the combined analysis. Figure 2 also shows that the classification accuracy was low when only a few features were used, indicating that the subset was too small to represent the characteristics of the entire dataset. When we increased the number of features used in the MCSD, the classification accuracy went up. The accuracy of classifying the testing dataset reached the highest value, 69.1, 52.7, and 90.9% on the miRNA expression, mRNA expression, and their combinations, respectively. However, more features may also add redundancy and thus cause the decrease of the classification accuracy. Therefore, we conclude that the use of fewer but significant features will achieve better classification accuracy.
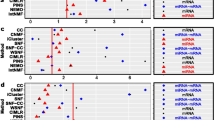
Figure 3a displays the normalized levels of the 121 selected features (118 mRNAs and 3 miRNAs) from both miRNA expression and mRNA expression data for the combined analysis, with the highest classification accuracy of 90.9%. If using the mRNA and miRNA data separately, they only give the accuracy as 49.1 and 47.3%, respectively. The samples with arrows were misclassified to the subtypes pointed by the arrows (e.g., the 17th sample that belongs to pro-neural was misclassified to classical). Each column represents a patient/sample and each row represents a feature (a probe from miRNA expression or mRNA expression data). The four subtypes of GBM are pro-neural, neural, classical, and mesenchymal. Each feature was normalized by the largest value in each row. It can be found that the misclassification only happens among the subtypes of pro-neural, neural, and classical. The number of misclassified samples in each subtype is one sample in pro-neural, two samples in neural, two samples in classical, and zero samples in mesenchymal. The expression levels in the subtype mesenchymal exhibit a significant difference from other three subtypes as shown in Figure 3a. Figure 3b displays the same selected features in the training dataset.
Display of the selected features in distinguishing the four subtypes of GBM, i.e., pro-neural (P), neural (N), classical (C), and mesenchymal (M) for the testing dataset (a) and the training dataset (b). 121 features (3 miRNA expression probes on the top and followed by 118 mRNA expression probes) were chosen from both miRNA expression and mRNA expression data. Each row represents a feature and each column represents a sample/patient. Each feature is normalized by the largest value in each row. The samples with arrows were misclassified to the subtypes as denoted by the arrow.
Conclusion and discussion
In this study, we applied the proposed MCSD to subtype four types of GBM: pro-neural, neural, classical, and mesenchymal with multiple genetic data from TCGA. High classification accuracy was achieved by using CS-based technique (i.e., MCSD) along with the combination of multiple datasets. The results from combining two types of genomic data were compared with those from single type of data. Moreover, the performance of the classification with and without MCSD technique had also been compared. The comparisons showed that the CS-based combined analysis of multiple types of genetic data could significantly improve the accuracy of detecting GBM subtypes.
Combining different types of genomic data allows us to interpret the information in the datasets comprehensively. The information from miRNA and mRNA are complementary to each other; so a combined analysis can give a better result than single data type analysis. miRNAs are a recently discovered class of small non-coding RNAs that regulate gene expression [25], which can be combined with mRNA data for better disease subtyping. However, if no dimension reduction with CS was applied, we found from Table 2 that the classification accuracy from combined analysis was comparable to that from the single mRNA expression because of the redundancy added. The classification performance was significantly improved after we used CS method, indicating that CS may reduce redundancy [26] in the combined datasets and thus improve the classification accuracy.
Informative features/biomarkers selected in this study have also been validated to be associated with GBM and have been reported in the literatures. In the combined data analysis, the 121 features/probes selected (shown in Additional file 2), the 3 miRNA expression probes and 118 mRNA expression probes are listed. Two of the selected miRNAs probes that represent the same miRNA, “hsa-miR-9” (sequence “TCATACAGCTAGATAACCAA”), have been validated to have stemness potential and chemoresistance to GBM cells [27–29], and known to be specifically expressed during brain neurogenesis. In the listed mRNA expression probes, the four probes of “CD44” and the three probes of “ASCL1” are selected. Both of the genes have been validated as biomarkers in subtyping GBM in multiple genomic studies [9, 30–32]. It demonstrates the significance of “CD44” and “ASCL1” in discriminating different subtypes of GBM. The three probes from “THBS1” are also selected in the 121 probes list. “THBS1” is a subunit of a disulfide-linked homotrimeric protein. This protein has been shown to play roles in platelet aggregation, angiogenesis, and tumorigenesis [33]. “THBS1” is also a major activator of “TGFB1” and the “TGFB1” expression is associated with GBM [34]. Moreover, it has been found that “TbRII”, a receptor of “TGFB1”, has a strong relationship with human malignant glioblastoma cells [35]. There are biomarkers listed in Additional file 2 that have not been reported yet. However, they may be potential biomarkers for GBM, deserving further study.
We also performed Gene Ontology (GO) analyses to determine that these genes were enriched in specific GO terms (biological processes). The GO term “antigen processing” and presentation “lymphocyte mediated immunity” (p = 1.78 × 10–6), and several GO terms related to wounding healing [e.g. “response to wounding” (p = 1.26 × 10–8); “wound healing” (p = 2.44 × 10–6)], and cell adhesion [e.g. “biological adhesion” (p = 6.53 × 10–7); “cell adhesion” (p = 6.41 × 10–7)] showed highly significant enrichment for our selected genes. These results were expected. Taking “lymphocyte mediated immunity”-related GO categories as an example, lymphocyte-mediated cellular responses play a critical role in the body’s ability to generate an antitumor immune response, and activation status of lymphocytes is an important determinant of sensitivity to tumor-mediated apoptosis [36]. In addition, according to previous studies, the miRNAs we identified are related to glioblastoma. For example, it was found that “has-miR-9” inhibit differentiation of glioblastoma stem cells, and the calmodulin-binding transcription activator 1 (CAMTA1) as “has-miR-9” target is a tumor suppressor in glioblastoma [37].
To test the stability of the classification results, the samples in training and testing were randomly rearranged ten more times. The number of samples from each subtype in training and testing was maintained the same as in the description in the section “Data collection”. The overall classification rate has an average value of 87.1% with a standard deviation of 4.5%, indicating that the results are rather robust.
In summary, we have developed a CS-based technique for combining multiple genomic data to subtype glioblastoma more accurately. The biomarkers identified with our approaches have also been validated or reported in some existing literatures, indicating that the integrated approach can provide comprehensive information for better disease diagnosis.
References
Leukemia-Topic Overview. http://www.webmd.com/cancer/tc/leukemia-topic-overview
Yeung KY, Bumgarner RE, Raftery AE: Bayesian model averaging: development of an improved multi-class, gene selection and classification tool for microarray data. Bioinformatics 2005, 21: 2394-2402. 10.1093/bioinformatics/bti319
Seungchan K, Dougherty ER, Shmulevich I, Hess KR, Hamilton SR, Trent JM, Fuller GN, Zhang W: Identification of combination gene sets for glioma classification. Mol. Cancer Ther. 2002, 1: 1229-1236.
Lapointe J, Li C, Higgins JP, Rijn M, Bair E, Montgomery K, Ferrari M, Egevad L, Rayford W, Bergerheim U, Ekman P, DeMarzo AM, Tibshirani R, Botstein D, Brown PO, Brooks JD, Pollack JR: Gene expression profiling identifies clinically relevant subtypes of prostate cancer. PNAS 2003, 101: 811-816.
Ohgaki H, Kleihues P: Epidemiology and etiology of gliomas. Acta Neuropathol. 2005, 109: 93-108. 10.1007/s00401-005-0991-y
Benjamin R, Capparella J, Brown A: Classification of glioblastoma multiforme in adults by molecular genetics. Cancer J. 2003, 9: 82-90. 10.1097/00130404-200303000-00003
Nutt CL, Mani DR, Betensky RA, Tamayo P, Cairncross JG, Ladd C, Pohl U, Hartmann C, McLaughlin ME, Batchelor TT, Black PM, Deimling AV, Pomeroy SL, Golub TR, Louis DN: Gene expression-based classification of malignant gliomas correlates better with survival than histological classification. Cancer Res. 2003, 63: 1602-1607.
Noushmehr H, Weisenberger DJ, Diefes K, Phillips HS, Pujara K, Berman BP, Pan F, Pelloski CE, Sulman EP, Bhat KP, Verhaak RGW, Hoadley KA, Hayes DN, Perou CM, Schmidt HK, Ding L, Wilson RK, Den Berg DV, Shen H, Bengtsson H, Neuvial P, Cope LM, Buckley J, Herman JG, Baylin SB, Laird PW, Aldape K: The cancer genome atlas research network. Identification of a CpG island methylator phenotype that defines a distinct subgroup of glioma. Cancer Cell 2010, 17: 510-522. 10.1016/j.ccr.2010.03.017
Verhaak RGW, Hoadley KA, Purdom E, Wang V, Qi Y, Wilkerson MD, Miller CR, Ding L, Golub T, Mesirov JP, Alexe G, Lawrence M, Kelly MO, Tamayo P, Weir BA, Gabriel S, Winckler W, Gupta S, Jakkula L, Feiler HS, Hodgson JG, James CD, Sarkaria JN, Brennan C, Kahn A, Spellman PT, Wilson RK, Speed TP, Gray JW, Meyerson M, et al.: Integrated genomic analysis identifies clinically relevant subtypes of Glioblastoma characterized by abnormalities in PDGFRA, IDH1, EGFR, and NF1. Cancer Cell 2010, 17: 98-110. 10.1016/j.ccr.2009.12.020
Bentwich I, Avniel A, Karov Y, Aharonov R, Gilad S, Barad O, Barzilai A, Einat P, Einav U, Meiri E, Sharon E, Spector Y, Bentwich Z: Identification of hundreds of conserved and nonconserved human microRNAs. Nat. Genet. 2005, 37: 766-770. 10.1038/ng1590
Fasanaro P, Greco S, Ivan M, Capogrossi M, Martelli F: MicroRNA: emerging therapeutic targets in acute ischemic diseases. Pharmacol. Ther. 2010, 125: 92-104. 10.1016/j.pharmthera.2009.10.003
Iorio MV, Ferracin M, Liu C-G, Veronese A, Spizzo R, Sabbioni S, Magri E, Pedriali M, Fabbri M, Campiglio M, Ménard S, Palazzo JP, Rosenberg A, Musiani P, Volinia S, Nenci I, Calin GA, Querzoli P, Negrini M, Croce CM: MicroRNA gene expression deregulation in human breast cancer. Cancer Res. 2005, 65: 7065-7070. 10.1158/0008-5472.CAN-05-1783
Bishop JA, Benjamin H, Cholakh H, Chajut A, Clark DP, Westra WH: Accurate classification of non-small cell lung carcinoma using a novel MicroRNA-based approach. Clin. Cancer Res. 2010, 16: 610-619. 10.1158/1078-0432.CCR-09-2638
Soneson C, Lilljebjörn H, Fioretos T, Fontes M: Integrative analysis of gene expression and copy number alterations using canonical correlation analysis. BMC Bioinforma 2010, 11: 191. 10.1186/1471-2105-11-191
Kingsley CB, Kuo W-L, Polikoff D, Berchuck A, Gray JW, Jain AN: Magellan: a web based system for the integrated analysis of heterogeneous biological data and annotations; application to DNA copy number and expression data in ovarian cancer. Cancer Inf. 2006, 2: 10-21.
Troyanskaya OG, Dolinski K, Owen AB, Altman RB, Botstein D: A Bayesian framework for combining heterogeneous data sources for gene function prediction (in Saccharomyces cerevisiae). PNAS 2003, 100: 8348-8353. 10.1073/pnas.0832373100
Lanckriet GRG, Bie TD, Cristianini N, Jordan MI, Noble WS: A statistical framework for genomic data fusion. Bioinformatics 2004, 20: 2626-2635. 10.1093/bioinformatics/bth294
Davenport MA, Wakin MB, Baraniuk RG: Detection and estimation with compressive measurements. Technical Report. 2007.
Cand`es EJ, Wakin MB: An introduction to compressive sampling. IEEE Signal Process. Mag. 2008,25(2):21-30.
Tang W, Cao H, Duan J, Wang Y-P: A compressed sensing based approach for subtyping of leukemia from gene expression data. J. Bioinfo. Comput. Biol. 2011, 9: 631-645. 10.1142/S0219720011005689
Edwards DC, Metz CE, Kupinski MA: Ideal observers and optimal ROC hypersurfaces in N-class classification. IEEE Trans. Med. Imag. 2004, 23: 891-895. 10.1109/TMI.2004.828358
Starks SA, Kreinovich V: Environmentally-oriented processing of multi-spectral satellite images: new challenges for Bayesian methods. Proceedings of the 17th International Workshop on Maximum Entropy and Bayesian Methods of Statistical Analysis, Boise, Idaho 1998, 271.
Efron B, Hastie T, Johnstone I, Tibshirani R: Least angle regression. Ann. Stat. 2004, 32: 407-451. 10.1214/009053604000000067
Volinia S, Calin GA, Liu C-G, Ambs S, Cimmino A, Petrocca F, Visone R, Iorio M, Roldo C, Ferracin M, Prueitt RL, Yanaihara N, Lanza G, Scarpa A, Vecchione A, Negrini M, Harris CC, Croce CM: A microRNA expression signature of human solid tumors defines cancer gene targets. PNAS 2006, 103: 2257-2261. 10.1073/pnas.0510565103
Tsaig Y, Donoho DL: Extensions of compressed sensing. Signal Process. 2006, 86: 549-571. 10.1016/j.sigpro.2005.05.029
Jeon H-M, Sohn Y-W, Oh S-Y, Kim S-H, Beck S, Kim S, Kim H: ID4 imparts chemoresistance and cancer stemness to glioma cells by derepressing miR-9*-mediated suppression of SOX2. Cancer Res. 2011, 71: 3410-3421. 10.1158/0008-5472.CAN-10-3340
Ko MH, Kim S, Hwang W, Ko HY, Kim YH, Lee DS: Bioimaging of the unbalanced expression of microRNA9 and microRNA9* during the neuronal differentiation of P19 cells. FEBS J. 2008, 275: 2605-2616. 10.1111/j.1742-4658.2008.06408.x
Yoo AS, Staahl BT, Chen L, Crabtree GR: MicroRNA-mediated switching of chromatin-remodelling complexes in neural development. Nature 2009, 460: 642-646.
Liang Y, Diehn M, Watson N, Bollen AW, Aldape KD, Nicholas MK, Lamborn KR, Berger MS, Botstein D, Brown PO, Israel MA: Gene expression profiling reveals molecularly and clinically distinct subtypes of glioblastoma multiforme. PNAS 2005, 102: 5814-5819. 10.1073/pnas.0402870102
Ariza A, López D, Mate JL, Isamat M, Musulen E, Pujol M, Ley A, Navas-palacios J: Role of CD44 in the invasiveness of glioblastoma multiforme and the noninvasiveness of meningioma: an immunohistochemistry study. Hum. Pathol. 1995, 26: 1144-1147. 10.1016/0046-8177(95)90278-3
Phillips HS, Kharbanda S, Chen R, Forrest WF, Soriano RH, Wu TD, Misra A, Nigro JM, Colman H, Soroceanu L, Williams PM, Modrusan Z, Feuerstein BG, Aldape K: Molecular subclasses of high-grade glioma predict prognosis, delineate a pattern of disease progression, and resemble stages in neurogenesis. Cancer Cell 2006, 9: 157-173. 10.1016/j.ccr.2006.02.019
Galvez AF, Huang L, Magbanua MMJ, Dawson K, Rodriguez RL: Differential expression of thrombospondin (THBS1) in tumorigenic and nontumorigenic prostate epithelial cells in response to a chromatin-binding soy peptide. Nutr. Cancer 2011, 63: 623-636. 10.1080/01635581.2011.539312
Lin B, Madan A, Yoon J-G, Fang X, Yan X, Kim T-K, Hwang D, Hood L, Foltz G: Massively parallel signature sequencing and bioinformatics analysis identifies up-regulation of TGFBI and SOX4 in human glioblastoma. PLoS One 2010, 5: e10210. 10.1371/journal.pone.0010210
Wesolowska A, Sliwa M, Kaminska B: Development of siRNA against TbRII blocking efficiently TGFb1 signaling pathways in glioma cells. Eur. J. Biochem. 2004, 271: 35-58. Supplement 1 July: abstract number P2.5-05
Chahlavi A, Rayman P, Richmond A-L, Biswas K, Zhang R, Vogelbaum M, Tannenbaum C, Barnett G, Finke J-H: Glioblastomas induce T-lymphocyte death by two distinct pathways involving gangliosides and CD70. Cancer Res. 2005, 65: 5428-5438. 10.1158/0008-5472.CAN-04-4395
Gil-Ranedo J, Mendiburu-Elicabe M, Garcia-Villanueva M, Medina D, del Alamo M, Izquierdo M: An off-target nucleostemin RNAi inhibits growth in human glioblastoma-derived cancer stem cells. PLoS One 2011, 6: e28753. 10.1371/journal.pone.0028753
Acknowledgments
This study was supported by the NIH grant R21 LM010042, NSF Advances in Biological informatics (ABI) grant and The Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning. The authors deeply appreciate the anonymous referees for their valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Electronic supplementary material
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License ( https://creativecommons.org/licenses/by-nc/2.0 ), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Tang, W., Duan, J., Zhang, JG. et al. Subtyping glioblastoma by combining miRNA and mRNA expression data using compressed sensing-based approach. J Bioinform Sys Biology 2013, 2 (2013). https://doi.org/10.1186/1687-4153-2013-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-4153-2013-2